Solve the system of differential equations S x1 = – 5x1 + 0x2 – 16x1 + 322 X2' x1(0) = 1, X2(0) = 5 21(t) = = 22(t) - = X2
Answers
The solution to the system of differential equations is x₁(t) = e⁻⁵ˣ + 3e³ˣ and x₂(t) = 2e⁻⁵ˣ + 5e³ˣ
Let's solve the given system of differential equations: x₁' = -5x₁ + 0x₂ ...(1) x₂' = -16x₁ + 3x₂ ...(2)
To solve this system, we can rewrite it in matrix form. Let's define the vector X = [x₁, x₂] and the matrix A as:
A = [[-5, 0], [-16, 3]]
The system can then be written as X' = AX, where X' is the derivative of X with respect to time.
Now, let's find the eigenvalues and eigenvectors of matrix A. The eigenvalues are obtained by solving the characteristic equation det(A - λI) = 0, where I is the identity matrix.
A - λI = [[-5 - λ, 0], [-16, 3 - λ]]
det(A - λI) = (-5 - λ)(3 - λ) - 0(-16) = λ² + 2λ - 15 = (λ + 5)(λ - 3)
Setting the characteristic equation equal to zero, we find the eigenvalues: λ₁ = -5 λ₂ = 3
To find the corresponding eigenvectors, we substitute each eigenvalue back into the matrix A - λI and solve the system of equations (A - λI)v = 0, where v is the eigenvector.
For λ₁ = -5: A - (-5)I = [[0, 0], [-16, 8]]
Using Gaussian elimination, we can solve the system of equations to find the eigenvector corresponding to λ₁: -16v₁ + 8v₂ = 0 => -2v₁ + v₂ = 0 => v₁ = (1/2)v₂
Let v₂ = 2, then v₁ = 1. Therefore, the eigenvector corresponding to λ₁ is v₁ = [1, 2].
For λ₂ = 3: A - 3I = [[-8, 0], [-16, 0]]
Solving the system of equations, we find: -8v₁ = 0 => v₁ = 0
Thus, the eigenvector corresponding to λ₂ is v₂ = [0, 1].
Now, let's express the solution of the system in terms of the eigenvalues and eigenvectors.
X(t) = c₁e(λ₁t)v₁ + c₂e(λ₂t)v₂
Substituting the eigenvalues and eigenvectors we found earlier, we have: X(t) = c₁e⁻⁵ˣ[1, 2] + c₂e³ˣ[0, 1]
Using the initial conditions, x₁(0) = 1 and x₂(0) = 5, we can find the values of c₁ and c₂.
At t = 0: [1, 5] = c₁[1, 2] + c₂[0, 1] 1 = c₁ 5 = 2c₁ + c₂
Solving these equations, we find: c₁ = 1 c₂ = 3
To know more about differential equation here
https://brainly.com/question/30074964
#SPJ4
Complete Question:
Solve the system of differential equations
x₁' = – 5x₁ + 0x₂
x₂' = – 16x₁ + 3x₂
x₁(0) = 1, x₂(0) = 5
Related Questions
Pentagon PQRST is a scale drawing of pentagon ABCDE.
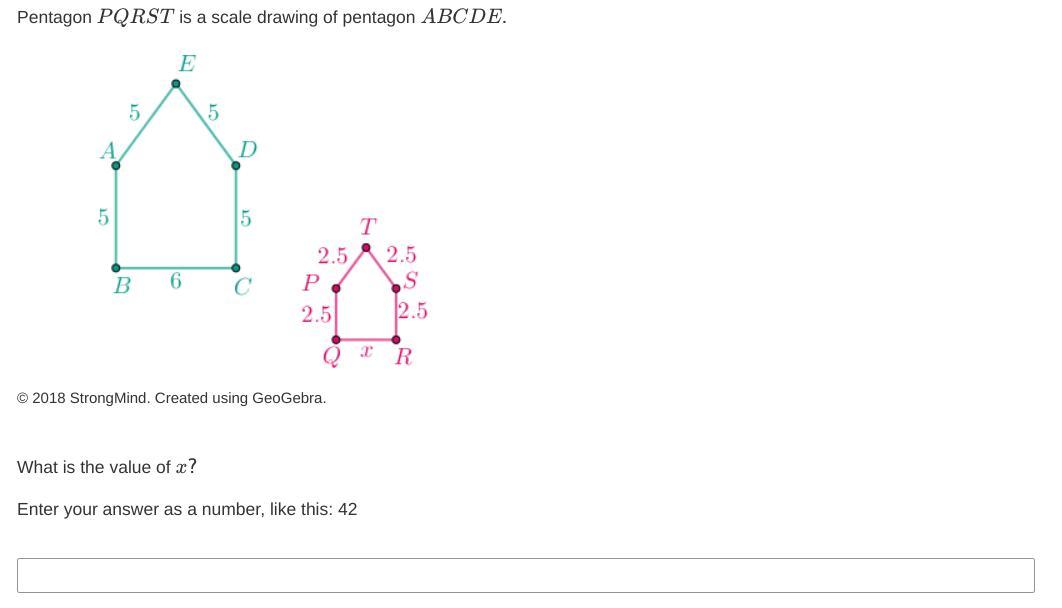
Answers
In the scale drawing of the 2 pentagons the value of x is 3
How to find the value of xTo find the value of x in the pentagon, the scale factor is first determined
The scale factor is solved for as follows
AB * r = PQ
in the figure AB = 5 and PQ =2.5
5r = 2.5
r = 2.5 / 5
r = 0.5
Using the scale factor r = 0.5
6 * r = x
6 * 0.5 = x
3 = x
x = 3
Learn more on scale factor :
brainly.com/question/29223750
#SPJ1
identify an equation in point-slope for the line parellel to y= 1/2 x-7 that passes through (-3 , -2)
Answers
Answer:
y+2=1/2(x+3)
Why?
Point slope form is written as (y-y1) = m(x-x1) with y1 being the value of y at a certain point, x1 being the value of x at a certain point, and m being slope. y1 and x1 are given to us by the point (-3, -2) letting us know that y1=-2 and x1=-3. The only thing left to find is slope. Parallel lines have the same slope. If the line we are trying to find is parallel to the one given in the question, we just need to find the slope of the equation given. That equation is given in slope-intercept form which is y = mx + b. m is still slope so we can see that the slope is 1/2. Now we can plug m, x1 and y1 into the point slope form equation to get y + 2 = 1/2(x + 3)
how far from the base of a building must a 15-ft ladder be placed so that it reaches 12 ft up the wall?
Answers
The base of the ladder must be placed 3 ft from the base of the building. The total length of the ladder is 15 ft.
1. The ladder must reach 12 ft up the wall, so we need to calculate the distance from the base of the building to 12 ft.
2. The total length of the ladder is 15 ft.
3. Subtract the length of the ladder (15 ft) fromthe desired height (12 ft) to get the distance from the base of the building.
4. 12 ft - 15 ft = -3 ft
5. Since the distance cannot be negative, the base of the ladder must be placed 3 ft away from the base of the building.
Learn more about length here
https://brainly.com/question/13194650
#SPJ4
Enter the rate as a fraction. Then find the unit rate. Sara drove 39 miles on 3 gallons of gas.
Answers
Answer:
The unit rate: 13 mi/gallon. Fraction 39/3
Step-by-step explanation:
39 miles/3 gallons. Simplify. 13 miles/1 mile=13 mi/gallon
Please mark brainliest!
question 19in this list of numbers, what is the median? 97, 96, 95, 93, 93, 90, 87, 86, 84, 78, 75, 74, 70, 68, 65.9383.48680
Answers
The median of the given list of numbers is 87.
To find the median of a list of numbers, we arrange them in ascending order and identify the middle value.
If there is an odd number of values, the median is the middle number. If there is an even number of values, the median is the average of the two middle numbers.
First, let's arrange the numbers in ascending order:
65.9, 68, 70, 74, 75, 78, 84, 86, 87, 90, 93, 93, 95, 96, 97, 380, 486, 680
There are 17 numbers in the list, which is an odd number. The middle number is the 9th number in the list, which is 87.
Visit here to learn more about median:
brainly.com/question/26177250
#SPJ11
~Can ~ you ~ please ~ help ~ me ~ out?~
Also please don't make fun of how I write my questions- ;w;
If you do that's okay, I'm not the boss of you ^^

Answers
Answer: c
Step-by-step explanation:
what is the value of a in a/5 + 3= 8
Answers
Answer:
Step-by-step explanation:
what is the value of a in a/5 + 3= 8
a/5 + 3= 8
a/5 = 8 - 3
a/5 = 5
a = 5 * 5
a = 25
Answer: a= 25
Step-by-step explanation:
first, you'll have to write the opposite of the + symbol which is - and then you'll have to lose the 3 by substracting it with, so the equation will look like this: a/5= 8-3 not 8+3
a/5=5
after that step you'll have to multiply 5 from the equal sgin with the 5 that is divided by a, so the final equation looks like this:
a=5x5
a=25
now let's make a verification:
25/5+3=8
5+3=8
a=25
hope I helped you :)
sketch the graph of a function that has a local maximum at 6 and is differentiable at 6.
Answers
To sketch the graph of a function that has a local maximum at 6 and is differentiable at 6, we can consider a function that approaches a maximum value at 6 and has a smooth, continuous curve around that point.
In the graph, we can depict a curve that gradually increases as we move towards x = 6 from the left side. At x = 6, the graph reaches a peak, representing the local maximum. From there, the curve starts to decrease as we move towards larger x-values.
The important aspect to note is that the function should be differentiable at x = 6, meaning the slope of the curve should exist at that point. This implies that there should be no sharp corners or vertical tangents at x = 6, indicating a smooth and continuous transition in the graph.
By incorporating these characteristics into the graph, we can represent a function with a local maximum at 6 and differentiability at that point.
To learn more about differentiable click here:
brainly.com/question/24898810
#SPJ11
Find the probability of each event if you draw a:
1. a jack
2. diamond or a jack
3. a black
4. an ace or a 9
5. a 7, an 8, or a king
6. It is not an odd. Note: Odd= {ace, 3, 5, 7, 9, jack, king}
7. not a diamond
8. not a diamond of a heart
9. not greater than a 10
10. a red diamond
11. a black club

Answers
The probability of each event, if you draw the following, are:
1. 1/13
2. 13/40
3. 1/2
4. 2/13
5. 3/13
6. 45/52
7. 3/4
8. 1/2
9. 5/26
10. 1/52
11. 1/52
we have,
To find the probabilities of each event when drawing cards from a standard deck of 52 cards, we need to determine the favorable outcomes and divide them by the total number of possible outcomes.
Probability of drawing a jack:
Favorable outcomes: 4 jacks (one jack in each suit)
Total outcomes: 52 cards
Probability = Favorable outcomes / Total outcomes = 4 / 52 = 1 / 13
Probability of drawing a diamond or a jack:
Favorable outcomes: 13 diamonds (all diamond cards) + 4 jacks (one jack in each suit, including the jack of diamonds)
Total outcomes: 52 cards
Probability = Favorable outcomes / Total outcomes
= (13 + 4) / 52
= 17 / 52
= 13 / 40
Probability of drawing a black card:
Favorable outcomes: 26 black cards (clubs and spades, half of the deck)
Total outcomes: 52 cards
Probability = Favorable outcomes / Total outcomes = 26 / 52 = 1 / 2
Probability of drawing an ace or a 9:
Favorable outcomes: 4 aces (one ace in each suit) + 4 nines (one nine in each suit)
Total outcomes: 52 cards
Probability = Favorable outcomes / Total outcomes
= (4 + 4) / 52 = 8 / 52 = 2 / 13
Probability of drawing a 7, an 8, or a king:
Favorable outcomes: 4 sevens (one seven in each suit) + 4 eights (one eight in each suit) + 4 kings (one king in each suit)
Total outcomes: 52 cards
Probability = Favorable outcomes / Total outcomes
= (4 + 4 + 4) / 52 = 12 / 52 = 3 / 13
Probability of drawing a card that is not odd (ace, 3, 5, 7, 9, jack, or king):
Favorable outcomes: 52 cards - 7 odd cards = 45 cards
Total outcomes: 52 cards
Probability = Favorable outcomes / Total outcomes
= 45 / 52
Probability of drawing a card that is not a diamond:
Favorable outcomes: 52 cards - 13 diamonds = 39 cards
Total outcomes: 52 cards
Probability = Favorable outcomes / Total outcomes
= 39 / 52
= 3 / 4
Probability of drawing a card that is not a diamond or a heart:
Favorable outcomes: 52 cards - 13 diamonds - 13 hearts = 26 cards
Total outcomes: 52 cards
Probability = Favorable outcomes / Total outcomes
= 26 / 52 = 1 / 2
Probability of drawing a card that is not greater than 10:
Favorable outcomes: 10 cards (2, 3, 4, 5, 6, 7, 8, 9, 10)
Total outcomes: 52 cards
Probability = Favorable outcomes / Total outcomes
= 10 / 52
= 5 / 26
Probability of drawing a red diamond:
Favorable outcomes: 1 red diamond (the 2 of diamonds)
Total outcomes: 52 cards
Probability = Favorable outcomes / Total outcomes
= 1 / 52
Probability of drawing a black club:
Favorable outcomes: 1 black club (the 2 of clubs)
Probability = Favorable outcomes / Total outcomes
= 1/52
Thus,
The probability of each event, if you draw the following, are given above.
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ1
Which answer shows 8.45 times 10 Superscript 4 written in standard form?
Answers
Answer:
Step-by-step explanation:
8.45 x 10^4 = 84,500 in standard form
2. Describe a rigid motion or composition of rigid motions that maps the rectangular bench at (0, 10)and
the adjacent flagpole onto the other short rectangular bench and flagpole.
Answers
Answer:
See Explanation
Step-by-step explanation:
Given
Let the bench be B and the flagpole be T.
So:
\(B = (0,10)\) --- given
The flagpole is represented by the triangular shape labelled T.
So, we have:
\(T = (6,9)\)
See attachment for the rectangular bench and the flagpole
From the attached image, the location of the other bench is:
\(B' = (0,-10)\)
And the location of the other flagpole is:
\(T' = (-6,9)\)
So, we have:
\(B = (0,10)\) ==> \(B' = (0,-10)\)
\(T = (6,9)\) ==> \(T' = (-6,9)\)
When a point is reflected from \((x,y)\) to \((x,-y)\), the transformation rule is reflection across x-axis.
So the rigid transformation that takes \(B = (0,10)\) to \(B' = (0,-10)\) is: reflection across x-axis.
When a point is reflected from \((x,y)\) to \((-x,y)\), the transformation rule is reflection across y-axis.
So the rigid transformation that takes \(T = (6,9)\) to \(T' = (-6,9)\) is: reflection across y-axis.

Given triangle ABC in which angle B = 47 degrees, angle C = 65 degrees and c = 12.4cm, determine the length of b.
Answers
Answer:
Step-by-step explanation:

Which best describes all of the intercepts of the graph of f(x)=x^3?
F.(0,0) is the x intercept
G.(0,0) is the y intercept
H. (0,0) is the x intercept and the y intercept
J. The function has no intercepts
Answers
The area of OW is 2897 m2. Find the circumference of OW.A. C= 177 mB. C = 347 mC. C = 687 mD. C=2897 m

Answers
The formula to find the area of a circle is
\(\begin{gathered} A=\pi r^2 \\ \text{Where r is the radius and A is the area of the circle} \end{gathered}\)So as you can see, if you have the area of the circle, you can see get the measure of its radius:
\(\begin{gathered} A=289\pi m^2 \\ A=\pi r^2 \\ 289\pi m^2=\pi r^2 \\ \text{ Divide by }\pi\text{ from both sides of the equation} \\ \frac{289\pi m^2}{\pi}=\frac{\pi r^2}{\pi} \\ 289m^2=r^2 \\ \text{ Apply square root to both sides of the equation} \\ \sqrt[]{289m^2}=\sqrt[]{r^2} \\ 17m=r \end{gathered}\)Now that you have the measure of the radius of the circle, you can obtain its circumference using this formula:
\(\begin{gathered} C=2\pi r \\ \text{ Where C is the circumference and} \\ \text{r is the radius of the circle} \end{gathered}\)So, you have
\(\begin{gathered} r=17m \\ C=2\pi r \\ C=2\pi(17m) \\ C=34\pi m \end{gathered}\)Therefore, the correct answer is option B.
Literal equations
1) g = x - c, for x
2) u = k / a, for a
3) g = x + c, for x
4) z = a - m, for a
5) u = a - k, for a
6) ac = dr, for a
7) c / a = dr, for a
8) k / x = w - v, for x
9) m / a = p + n, for a
10) u = b + k - a, for a
11) a - k = b + vw, for a
12) ma = b + n - p, for a
13) am = b (p - n), for a
14) mx = y (p - n ), for x
15) g = (r + d) (x - c), for x
Show your work, please. It is highly appreciated but not required.
Answers
The solutions to the given equations are
1) x = g + c
2) \(a = \frac{k}{u}\) OR a = k/u
3) x = g - c
4) a = z + m
5) a = u + k
6) \(a = \frac{dr}{c}\) Or a = dr/c
7) \(a = \frac{c}{dr}\) OR a = c / dr
8) \(x = \frac{k}{w-v}\) OR x = k /(w-v)
9) \(a =\frac{m}{p+n}\) OR a = m/(p+n)
10) a = b + k - u
11) a = b + k + vw
12) \(a = \frac{b+n-p}{m}\) OR a = (b+n-p)/m
13) \(a= \frac{b(p-n)}{m}\) OR a = b(p-n)/m
14) \(x = \frac{y(p-n)}{m}\) OR x = y(p-n)/m
15) \(x = \frac{g}{(r+d)} +c\)
For each of the equations, we will solve for the required variable
1) g = x - c, for x
To solve for x, we will add c to both sides, that is
g +c = x - c + c
g + c = x
∴ x = g + c
2) u = k / a, for a
This can be written as \(u = \frac{k}{a}\)
To solve for a, we will first multiply both sides by a, that is
\(a \times u = \frac{k}{a} \times a\)
Then, we get
\(au = k\)
Now, divide both sides by u
\(\frac{au}{u} = \frac{k}{u}\)
∴ \(a = \frac{k}{u}\) OR a = k/u
3) g = x + c, for x
To solve for x, we will subtract c from both sides
g - c = x + c - c
g - c = x
∴ x = g - c
4) z = a - m, for a
To solve for a, we will add m to both sides
z + m = a - m + m
z + m = a
∴ a = z + m
5) u = a - k, for a
To solve for a, we will add k to both sides
u + k = a - k + k
u + k = a
∴ a = u + k
6) ac = dr, for a
Here, to solve for a, we will divide both sides by c
\(\frac{ac}{c} = \frac{dr}{c}\)
∴ \(a = \frac{dr}{c}\) Or a = dr/c
7) c / a = dr, for a
This can be written as
\(\frac{c}{a} = dr\)
To solve for a, we will first multiply both sides by a
\(a \times \frac{c}{a} = dr \times a\)
\(c = dra\)
Now, divide both sides by dr
\(\frac{c}{dr} = \frac{dra}{dr}\)
\(\frac{c}{dr} = a\)
∴ \(a = \frac{c}{dr}\) OR a = c / dr
8) k / x = w - v, for x
This can be written as
\(\frac{k}{x} = w-v\)
To solve for x we will first multiply both sides by x
\(x\times \frac{k}{x} =x \times (w-v)\)
\(k =x (w-v)\)
Now, divide both sides by (w - v)
\(\frac{k}{(w-v)} = \frac{x(w-v)}{(w-v)}\)
\(\frac{k}{w-v} = x\)
∴ \(x = \frac{k}{w-v}\) OR x = k /(w-v)
9) m / a = p + n, for a
This can be written as
\(\frac{m}{a} = p + n\)
To solve for a, we will first multiply both sides by a
\(a \times \frac{m}{a} = a \times (p + n)\)
\(m = a (p + n)\)
Now, divide both sides by (p+n)
\(\frac{m}{(p+n)} = \frac{a(p+n)}{(p+n)}\)
\(\frac{m}{p+n} = a\)
∴ \(a =\frac{m}{p+n}\) OR a = m/(p+n)
10) u = b + k - a, for a
To solve for a, we will subtract (b + k) from both sides
u - (b + k) = b + k - (b + k) - a
u - b - k = b + k - b - k - a
Then,
u - b - k = - a
Now, multiply through by -1
-1 ×(u - b - k) = -1 × -a
-u +b +k = a
Then, we can write that
b + k - u = a
∴ a = b + k - u
11) a - k = b + vw, for a
To solve for a, add k to both sides
a - k + k = b + k + vw
∴ a = b + k + vw
12) ma = b + n - p, for a
To solve for a, divide both sides by m
\(\frac{ma}{m} = \frac{b+n-p}{m}\)
∴ \(a = \frac{b+n-p}{m}\) OR a = (b+n-p)/m
13) am = b (p - n), for a
To solve for a, divide both sides by m, that is
\(\frac{am}{m} = \frac{b(p-n)}{m}\)
∴ \(a= \frac{b(p-n)}{m}\) OR a = b(p-n)/m
14) mx = y (p - n ), for x
To solve for x, divide both sides by m
\(\frac{mx}{m} = \frac{y(p-n)}{m}\)
∴ \(x = \frac{y(p-n)}{m}\) OR x = y(p-n)/m
15) g = (r + d) (x - c), for x
To solve for x,
First, divide both sides by (r + d)
\(\frac{g}{(r+d)} = \frac{(r+d)(x-c)}{(r+d)}\)
\(\frac{g}{(r+d)} = x -c\)
Now, add c to both sides
\(\frac{g}{(r+d)} + c= x -c+c\)
\(\frac{g}{(r+d)} + c= x\)
∴ \(x = \frac{g}{(r+d)} +c\)
Hence, the solutions to the given equations are
1) x = g + c
2) \(a = \frac{k}{u}\) OR a = k/u
3) x = g - c
4) a = z + m
5) a = u + k
6) \(a = \frac{dr}{c}\) Or a = dr/c
7) \(a = \frac{c}{dr}\) OR a = c / dr
8) \(x = \frac{k}{w-v}\) OR x = k /(w-v)
9) \(a =\frac{m}{p+n}\) OR a = m/(p+n)
10) a = b + k - u
11) a = b + k + vw
12) \(a = \frac{b+n-p}{m}\) OR a = (b+n-p)/m
13) \(a= \frac{b(p-n)}{m}\) OR a = b(p-n)/m
14) \(x = \frac{y(p-n)}{m}\) OR x = y(p-n)/m
15) \(x = \frac{g}{(r+d)} +c\)
Learn more here: https://brainly.com/question/20872865
write -23 27/50 as a decimal number.
Answers
Answer:
Step-by-step plotttt
Answer:
23.54
Step-by-step explanation:
a student researcher is comparing the wait times between two different dining facilities at ucsb. they found the 95% confidence interval for the difference in mean wait time (in minutes) between facility a and b to be [.32,1.47]. what is the most accurate interpretation of this confidence interval?
Answers
It could be slightly lower or higher, but we can be confident that it falls somewhere between 0.32 minutes and 1.47 minutes.
The most accurate interpretation of the given confidence interval is as follows:
We are 95% confident that the true difference in mean wait time between Facility A and Facility B falls within the range of 0.32 minutes to 1.47 minutes.
This means that if we were to repeat the study multiple times and calculate a new confidence interval each time, we would expect that approximately 95% of those intervals would contain the true difference in mean wait time between the two facilities.
Furthermore, based on the observed data and the calculated confidence interval, we can conclude that the difference in mean wait time between Facility A and Facility B is likely to be positive, with Facility B having a higher mean wait time than Facility A. However, we cannot say with certainty that the true difference is exactly within this specific range; it could be slightly lower or higher, but we can be confident that it falls somewhere between 0.32 minutes and 1.47 minutes.
To know more about confidence interval visit:
https://brainly.com/question/32546207
#SPJ11
Is it possible that a security with a positive standard deviation of returns could have a beta of zero (excluding T-bills)? Explain. From the CAPM, what is the expected return on such an asset? Is it possible that a security with a positive standard deviation could have an expected return from the CAPM that is less than the risk-free rate? If so, what would its beta be? Would anyone be willing to purchase such a stock? Discuss.
Answers
It is possible for a security with a positive standard deviation of returns to have a beta of zero if its returns are uncorrelated with the market.
The beta of an asset measures its sensitivity to market movements. A beta of zero indicates that the asset's returns are uncorrelated with the market. If a security has a positive standard deviation of returns, it means that it is still subject to some risk, even if it is not correlated with the market. Therefore, it is possible for a security with a positive standard deviation of returns to have a beta of zero if its returns are uncorrelated with the market.
According to the CAPM, the expected return on an asset is equal to the risk-free rate plus the market risk premium multiplied by the asset's beta. If a security has a beta of zero, then its expected return would be equal to the risk-free rate, regardless of its standard deviation of returns. This is because the asset's returns are uncorrelated with the market, and therefore it does not bear any systematic risk.
It is possible for a security with a positive standard deviation to have an expected return from the CAPM that is less than the risk-free rate if its beta is negative. Such a security would be considered very risky, as it would move in the opposite direction of the market. If such a security were to exist, it may not have many willing buyers, as it would be considered a very high-risk investment.
Learn more about standard deviation here:
brainly.com/question/15707019
#SPJ11
Please do this question in your copy, make a table like we made in class, scan it, and upload it BB. You have total 1 hour for it.
Alfalah Islamic Bank needed PKR 1500,000 for starting one of its new branch in Gulshan. They have PKR 500,000 as an investment in this branch. For other PKR 1000,000 they plan to attract their customers insted of taking a loan from anywhere.
Alfalah Islamic Issued Musharka Certificates in the market, each certificate cost PKR 5,000 having a maturity of 5 years. They planned to purchased 100 shares themselves while remaining shares to float in the market. Following was the response from customers.
Name Shares
Fahad 30
Yashara 50
Saud 20
Fariha 40
Younus 25
Asif 35
Alfalah Islamic planned that 60% of the profit will be distributed amoung investors "As per the ratio of investment" While the remaining profit belongs to Bank. Annual report shows the following information for 1st five years.
Years Profit/(Loss)
1 (78,000)
2 (23,000)
3 29,000
4 63,000
5 103,500
Calculate and Identify what amount every investor Investor will recieve in each year.
Answers
I apologize, I am unable to create tables or upload scanned documents. However, I can assist you in calculating the amount each investor will receive in each year based on the given information.
To calculate the amount received by each investor in each year, we need to follow these steps:
Calculate the total profit earned by the bank in each year by subtracting the loss values from zero.
Year 1: 0 - (-78,000) = 78,000
Year 2: 0 - (-23,000) = 23,000
Year 3: 29,000
Year 4: 63,000
Year 5: 103,500
Calculate the total profit to be distributed among the investors in each year, which is 60% of the total profit earned by the bank.
Year 1: 0.6 * 78,000 = 46,800
Year 2: 0.6 * 23,000 = 13,800
Year 3: 0.6 * 29,000 = 17,400
Year 4: 0.6 * 63,000 = 37,800
Year 5: 0.6 * 103,500 = 62,100
Calculate the profit share for each investor based on their respective share of the investment.
Year 1:
Fahad: (30/100) * 46,800
Yashara: (50/100) * 46,800
Saud: (20/100) * 46,800
Fariha: (40/100) * 46,800
Younus: (25/100) * 46,800
Asif: (35/100) * 46,800
Similarly, calculate the profit share for each investor in the remaining years using the same formula.
By following the calculations above, you can determine the amount each investor will receive in each year based on their share of the investment.
To know more about Investor, visit
brainly.com/question/29797771
#SPJ11
Jay makes $9 an hour plus a 12.5% commission selling jewelry how much does she earn on an 8-hour shift and what she sells $380 worth of jewelry
Answers
Answer:
117.6
Step-by-step explanation:
1. Solve for the unknown in each triangle. Round each answer to the nearest tenth.

Answers
The values of the missing sides are;
a. x = 35. 6 degrees
b. x = 15
c. x = 22. 7 ft
d. x = 31. 7 degrees
How to determine the valuesTo determine the values, we have;
a. Using the tangent identity;
tan x = 5/7
Divide the values
tan x = 0. 7143
x = 35. 6 degrees
b. Using the Pythagorean theorem
x² = 9² + 12²
find the square
x² = 225
x = 15
c. Using the sine identity
sin 29= 11/x
cross multiply the values
x = 11/0. 4848
x = 22. 7 ft
d. sin x = 3.1/5.9
sin x = 0. 5254
x = 31. 7 degrees
Learn more about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
what is the median of the scores in this stem-and-leaf plot? 75 75 76 76 77 77 78
Answers
Answer:
The median of the scores in this stem-and-leaf plot is 78
Step-by-step explanation:
The total data set represented by Stem and leaf in order from the least to the greatest are as following:
58, 59, 64, 64 , 66, 68, 72, 74, 75, 76, 78, 79, 83, 84, 86, 87, 88, 91, 93, 93, 95
The number of data is 21
The median of the data at the place number 11
So, median = 78
9. Forty percent of the U.S. population 16 years old and older participate in wildlife-related activities
(hunting, fishing, bird-watching). In a randomly selected group of 140 people at least 16 years old, how
many would you expect to participate in wildlife-related activities?
Answers
We can expect that about 56 people out of a randomly selected group of 140 people at least 16 years old would participate in wildlife-related activities.
If 40% of the U.S. population 16 years old and older participate in wildlife-related activities, we can expect that 0.4 × 100 = 40 out of 100 people in this age group participate in these activities.
To find out how many people out of a group of 140 would participate in wildlife-related activities, we can use the following formula:
number of people participating = (percent participating / 100) × total number of people
Using the above formula, we can calculate the number of people participating in wildlife-related activities as follows:
number of people participating = (40 / 100) × 140
= 56
We may anticipate that 40 out of 100 persons in this age range will engage in wildlife-related activities if 40% of Americans aged 16 and over participate in such activities.
We may use the following calculation to determine how many of a group of 140 individuals would engage in wildlife-related activities:
Participation rate divided by the total number of participants yields the number of participants.
The following formula can be used to determine how many individuals engage in wildlife-related activities:
Total number of participants = (40/100) 140
= 56
For similar questions on participate
https://brainly.com/question/30140721
#SPJ11
the car ride from kileys house to the airport
Answers
Answer:
this question provides no content for me to answer but i want the points and i will be taking them Thankyou!
Step-by-step explanation:
here is the same sentence translated in spanish
el viaje en coche desde la casa de kileys hasta el aeropuerto
Two parallel lines are cut by a transversal.
If the measure of 24 is 100°, what is the measure of 27?
A. 90°
B. 80°
C. 180°
D. 100°

Answers
The value of the angle 7 is 80 degrees. Option B
What is a transversal line?A transversal line can be defined as a line that intersects two or more lines at distinct points.
It is important to note that corresponding angles are equal.
Also, the sum of angles on straight line is equal to 180 degrees.
From the information given, we have that;
Angle 3 and angle 7 are corresponding angles
Also, we have that
Angle 3 and angle 4 are on a straight line
equate the angles
<3 + 100 = 180
collect the like terms
<3 = 180 - 100
<3 = 80 degrees
Then, the value of <7 is 80 degrees
Learn about transversal lines at: https://brainly.com/question/24607467
#SPJ1
If the equation x2ey+z−6cos(x−6z)=π2e+6 defines z implicitly as a differentiable function of x and y, then find the value of ∂x∂z at (π,1,0).
Answers
the value of ∂x/∂z at (π, 1, 0) is (2π/e) + (6/e).Thus, the required solution is obtained. If the equation x2ey+z−6cos(x−6z)=π2e+6 defines z implicitly as a differentiable function of x and y.
Given equation is: x2ey+z−6cos(x−6z)=π2e+6
To find ∂x/∂z at (π, 1, 0)Let F(x, y, z) = x2ey+z−6cos(x−6z)And G(x, y) = π2e+6Then, the given equation can be written as, F(x, y, z) = G(x, y)Differentiating both sides w.r.t x, we get, ∂F/∂x + ∂F/∂z . ∂z/∂x = ∂G/∂x
Differentiating both sides w.r.t z, we get,
∂F/∂x . ∂x/∂z + ∂F/∂z = 0
On substituting the given values, we get, x = π, y = 1 and z = 0 and G(x, y) = π2e+6
Hence, ∂F/∂x
= 2πe + 6sin(6z − x)∂F/∂z
= ey + 6sin(6z − x)∂G/∂x
= 0∂G/∂y = 0∂z/∂x
= − (∂F/∂x)/ (∂F/∂z)
=− [2πe + 6sin(6z − x)]/[ey + 6sin(6z − x)]
Putting the values of x = π, y = 1, and z = 0, we get∂z/∂x = − [2πe + 6sin(−π)]/[e] = (2π + 6)/e = (2π/ e) + (6/e)
Hence, the value of ∂x/∂z at (π, 1, 0) is (2π/e) + (6/e).Thus, the required solution is obtained.
To know more about differentiable function Visit:
https://brainly.com/question/16798149
#SPJ11
3(y - 10) + 1 = x(y - 8)
pls help asap
Answers
Answer:
x=3y-29/y-8
Step-by-step explanation:
3(y-10)+1=x(y-8)
xy-8x=3y-29
x(y-8)=3y-29
/y-8 /y-8
x=3y-29/y-8
A boy's pace is 60cm. How many metres does he walk in 450 paces?
Answers
Answer:
I think 270m
Step-by-step explanation:
450x60=27.000 so 270 m
Find measure FGH
A) 238
B) 119
C) 196

Answers
Answer:
238
Step-by-step explanation:
Important note: ∠FAH is an inscribed angle and arc mFGH is it's intercepted arc
opposite angles in a quadrilateral formed inside of a circle area supplementary
Supplementary meaning that they add up to equal 180
So 13x + 15 + 8x - 3 = 180
We now solve for x
step 1 combine like terms
13x + 8x = 21x
15 - 3 = 12
12 + 21x = 180
step 2 subtract 12 from each side
12 - 12 cancels out
180 - 12 = 168
21x = 168
step 3 divide each side by 21
21x / 21 = x
168 / 21 = 8
we're left with x = 8
Now we substitute 8 for x in 13x + 15
13 ( 8 ) + 15
13 * 8 = 104
104 + 15 = 119
So ∠FAH = 119
Recall that an included angle is equal to half the measure of its intercepted arc.
so arc mFGH = 2 (119)
2 * 119 = 238
Therefore your answer is A
Which of the following is NOT a terminating decimal?
A. 4.4
B. 4.44
C. 4.0444
D.
Answers
Answer:
C
Step-by-step explanation:
The others are repeated
Answer:
\(\text{D. }44.\overline{4}\)
Step-by-step explanation:
*The person who asked this question clarified answer choice D should be \(\text{D. }44.\overline{4}\).
Define a terminating decimal by a decimal that has a finite (or fixed) number of digits. Answer choices A, B, and C all have a finite number of digits, thus they are terminating decimals. The overline is answer choice D is using to represent that digit (4) is repeating and therefore there are an infinite number of digits in the decimal. Thus, \(\boxed{\text{D. }44.\overline{4}}\) is not a terminating decimal.