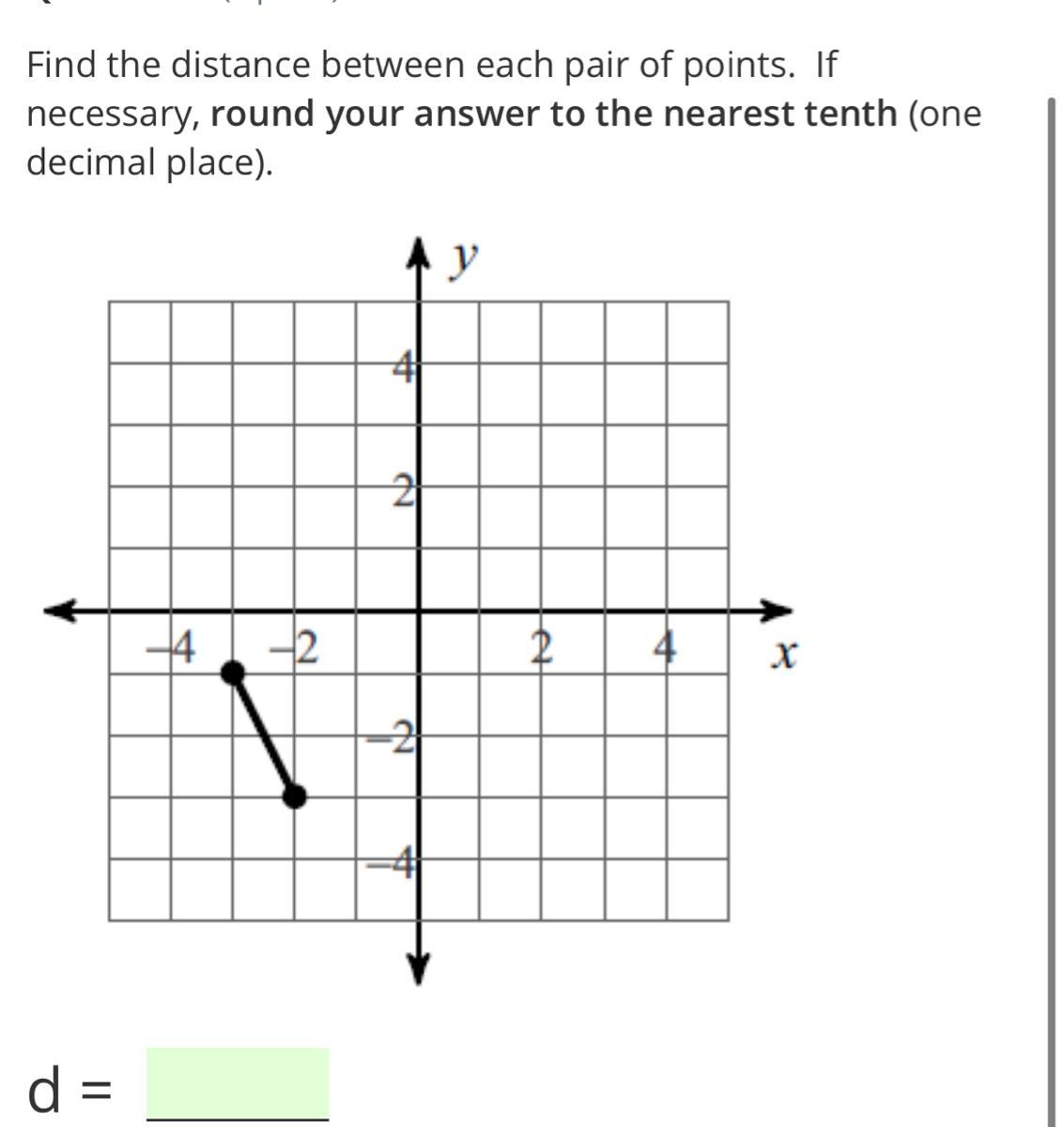
Answers
Given:
The graph of a line segment.
To find:
The distance between the pair of points.
Solution:
From the given graph it is clear that the end points of the line segment are (-3,-1) and (-2,-3).
The distance between these two points is:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
\(d=\sqrt{(-2-(-3))^2+(-3-(-1))^2}\)
\(d=\sqrt{(-2+3)^2+(-3+1)^2}\)
\(d=\sqrt{(1)^2+(-2)^2}\)
On further simplification, we get
\(d=\sqrt{1+4}\)
\(d=\sqrt{5}\)
\(d=2.236067\)
\(d\approx 2.2\)
Therefore, the distance between the pair of point is about 2.2 units.
Related Questions
the quation is 8=z/6 please help me solve this algebraic equation......
Answers
Answer:
to find z
Step-by-step explanation:
8=z/6
z=6 x 8
z= 48
Find the height of the basketball hoop using similarity ratios. Explain step by step.

Answers
The height of the basketball hoop is 13.32'.
What is law of similarity?
The Law of Similarity in mathematics states that if two geometric figures have the same shape but different sizes, then they are considered similar. This means that the corresponding angles of the two figures are congruent, and the corresponding sides are proportional in length.
Formally, if we have two geometric figures A and B, and if every angle of figure A is congruent to the corresponding angle of figure B, and if the ratio of the length of any pair of corresponding sides of A and B is constant, then we can say that A and B are similar figures.
Here we can see two triangle and base of two triangle is given.
Here base of small triangle is 12' and the base of big triangle is (12'+25') = 37'.
It is also given that height of small triangle is 4'3.84".
Now we want to find the height of the basketball hoop which is equal to height of big triangle.
Let the height of the basketball hoop be x.
So, by law of similarity ratios,
12'/37' = 4'3.84"/x
Now, 4'3.84" = 4.32'
So, 12'/37' = 4.32'/x
Therefore, x = 13.32'
Therefore, the height of the basketball hoop is 13.32'.
Learn more about triangle here,
https://brainly.com/question/27827375
#SPJ1
if the point in the upper left corner of the scatterplot is removed, what will happen to the correlation (r) and the slope of the line of best fit (b)?
Answers
The answer is A) i.e. Both will increase.
If the point in the upper left corner of the Explanatory variable versus the Response variable scatterplot is removed, the correlation (r) and the slope of the line of best fit (b) will change.
In a data graph or dataset you're dealing with, an outlier is a data point that is unusually high or unusually low in comparison to the closest data point and the rest of the nearby coexisting values. if the point is an outlier, removing it will increase the correlation (r) and the slope of the line of best fit (b).
Therefore, the answer is A) Both will increase.
Learn more about Outliner here
https://brainly.com/question/26958242
#SPJ4
Given question is incomplete, the complete question is below
If the point in the upper left corner of the Explanatory variable versus the Response variable scatterplot shown below is removed, what will happen to the correlation (r) and the slope of the line of best fit (b) ?
Possible answers
A) Both will increase
B) r will increase and b will decrease
C) They will not change
D) r will decrease and b will increase
E) Both will decrease
log and powers: Write the following numbers in the form a bi (recall that powers and log’s are not uniquely defined) with a, b ∈ r. • log(1) • log(−1) • log(i) • ii
Answers
Log(1), log(-1), log(i) and ii are all numbers written in the form a + bi. Log(1) = 0; log(-1) = undefined; log(i) = 0.5i; ii = -1; a = -1 and b = 0 because the number is in the form a + bi.
Given numbers are;• log(1)• log(-1)• log(i)• iiFor all numbers written in the form a + bi, we must find a and b. Here's how to do it: log(1)In this case, the log is taken in base 10. The result of this is 0. So, we have: log(1) = 0Therefore, a=0 and b=0 because the number is not in the form a + bi. log(-1)In this case, the log is taken in base 10. The result of this is undefined. This is because there is no power to which we can raise 10 to get -1. So, we have: log(-1) = undefinedTherefore, a=undefined and b=undefined because the number is not in the form a + bi. log(i)In this case, the log is taken in base 10. The result of this is 0.5iπ. So, we have: log(i) = 0.5iπTherefore, a=0 and b=0.5π because the number is in the form a + bi. iiIn this case, we are finding the square of i. i is a complex number given as i = 0 + 1i. Therefore, we have: i2 = (0 + 1i)2= (0)2 + 2(0)(1i) + (1i)2= -1This is because i2 = -1. Now, we can write ii as: ii = i × i= (0 + 1i) × (0 + 1i)= 0 + 0i + 0i + 1i2= -1So, we have: ii = -1Therefore, a=-1 and b=0 because the number is in the form a + bi.
To know more about Logrithm Visit:
https://brainly.com/question/32630067
#SPJ11
suppose that 1% of the students at a particular college have the h1n1 influenza virus. 1. if a student gets together with 27 other college students over a period of time, what is the theoretical probability that at least one of those 27 students has the h1n1 influenza virus? show as a percentage with 3 decimal places.
Answers
There is a theoretical probability of approximately 26.2% that at least one of the 27 students in the group has the H1N1 influenza virus.
To calculate the theoretical probability that at least one of the 27 students has the H1N1 influenza virus, we can use the complement rule. The complement of the event "none of the 27 students have the H1N1 influenza virus" is the event "at least one of the 27 students has the H1N1 influenza virus."
The probability that a student does not have the H1N1 influenza virus is 1 - 0.01 = 0.99. Since the students are selected independently, the probability that none of the 27 students have the virus is (0.99)^27.
Using the complement rule, the probability that at least one of the 27 students has the H1N1 influenza virus is:
1 - (0.99)^27 ≈ 0.262
Expressed as a percentage with 3 decimal places, the theoretical probability is approximately 26.2%.
Know more about theoretical probability here:
https://brainly.com/question/30604977
#SPJ11
An estimator is consistent if as the sample size decreases, the value of the estimator approaches the value of the parameter estimated. (True or False)
Answers
The statement "An estimator is consistent if as the sample size decreases, the value of the estimator approaches the value of the parameter estimated" is False.
Consistency is an important property of estimators in statistics. An estimator is consistent if its value approaches the true value of the parameter being estimated as the sample size increases.
In other words, if we repeatedly take samples from the population and compute the estimator, the values we obtain will be close to the true parameter value.
This is an essential characteristic of a good estimator, as it ensures that as more data is collected, the estimation error decreases.
However, as the sample size decreases, the value of the estimator is more likely to deviate from the true value of the parameter. The reason for this is that a small sample size may not be representative of the population, and as a result, the estimation error may increase.
As a consequence, the statement is false. In conclusion, consistency is a property that an estimator possesses when its value converges to the true value of the parameter as the sample size grows.
As the sample size decreases, the estimator may become less reliable, leading to an increase in the estimation error.
For similar question on parameter:
https://brainly.com/question/12393177
#SPJ11
PLASE HELPpp it’s due before midnight. change to scientific notation
Q1: 9.6 x 10'7 =
Q2: 2 x 10'-6 =

Answers
2: 0.000002
Answer: Q1: 9.6e7
Q2: 2e-6
Step-by-step explanation: All you do is pretend the 10 insent their and and the e between the first set of numbers and the second number on the second set of numbers. Hope this helped!!!
LO
5
Select all the ways that zero can be
classified. select all that applied. (1 Point)
Whole number
Integer
rational number
Real number
none of the above
Answers
Answer:
?
Step-by-step explanation:
literally like ready work lol
show work?

Answers
Answer:
The pattern is of +5,+10,+20,+40
As 7+5=12
12+10=22
22+20=42
So the next three numbers are
42+40=82
82+80=162
163+160=323
figure A is a scale copy of figure B

Answers
The value of x is 42.
To determine the value of x, we need to analyze the given information regarding the scale factor between Figure A and Figure B.
The scale factor is expressed as the ratio of the corresponding side lengths or dimensions of the two figures.
Let's assume that the length of a side in Figure B is represented by 'x'. According to the given information, Figure A is a scale copy of Figure B with a scale factor of 2/7. This means that the corresponding side length in Figure A is 2/7 times the length of the corresponding side in Figure B.
Applying this scale factor to the length of side x in Figure B, we can express the length of the corresponding side in Figure A as (2/7)x.
Given that the length of side x in Figure B is 12, we can substitute it into the equation:
(2/7)x = 12
To solve for x, we can multiply both sides of the equation by 7/2:
x = (12 * 7) / 2
Simplifying the expression:
x = 84 / 2
x = 42
For more such questions on value
https://brainly.com/question/843074
#SPJ8
evaluate ∮cxdx ydyx2 y2, where c is any jordan curve whose interior does not contain the origin, traversed counterclockwise. ∮cxdx ydyx2 y2=
Answers
The value of the line integral ∮c x dx + y dy / \((x^2 + y^2)\), where c is any Jordan curve whose interior does not contain the origin, traversed counterclockwise, is 0.
To evaluate the line integral ∮c x dx + y dy / \((x^2 + y^2)\), where c is any Jordan curve whose interior does not contain the origin, traversed counterclockwise, we can apply Green's theorem.
Green's theorem states that for a vector field F = P(x, y) i + Q(x, y) j, and a simple closed curve C with positively oriented boundary, the line integral of F along C is equal to the double integral of the curl of F over the region enclosed by C.
In this case, the vector field F = x i + y j, and the line integral becomes ∮c x dx + y dy / \((x^2 + y^2)\) = ∬R curl(F) dA.
The curl of F is given by curl(F) = (∂Q/∂x - ∂P/∂y) k = (1 - 1) k = 0.
Since the curl of F is zero, the line integral becomes ∬R 0 dA = 0.
Therefore, the value of the line integral ∮c x dx + y dy / \((x^2 + y^2)\), where c is any Jordan curve whose interior does not contain the origin, traversed counterclockwise, is 0.
To learn more about line integral from the given link
https://brainly.com/question/31421669
#SPJ4
Choose the solids with approximately equal volumes.
9 cm:
5 cm
6 cm
9 cm
11 cm
cm
14
9 cm
9 cm
13 cm
-cm
14

Answers
Answer:
Adding 12 to the circle area is equal to the square area.
Or
s2 = 12 + A
Where
s = side of square
A = area of circle
So
s2 = 12 + 36
s2 = 48
Solve this for s to get the side length
Answer: It's the first cone (9cm, 9cm), the cylinder at the bottom (9cm, 3cm), and the sphere at the bottom (9/3sqrt4cm).
Step-by-step explanation: I got this right on Edmentum.

what is the domain of the following:
{(1,-2), (-2,0), (-1,2), (1,3)}
THANK YOU!
Answers
Answer: subtract
Step-by-step explanation:
look at it
Answer:
{-2,-2,1}
Step-by-step explanation:
Domain is the x's. Don't repeat the x's and go from least to highest.
I need help with questions 10,11,12,13.
Thanks!

Answers
Answer:
1:2
4:1
1:5
5:7
I can't really give a step by step but just find the distance for the numerator and denominator and simplify
What evidence is needed to prove two triangles are similar by the SSS similarity theorem?
Answers
Consider the same figure as given above. It is observed that DP/PE = DQ/QF and also in the triangle DEF, the line PQ is parallel to the line EF.
So, ∠P = ∠E and ∠Q = ∠F.
Hence, we can write: DP/DE = DQ/DF= PQ/EF.
The above expression is written as
DP/DE = DQ/DF=BC/EF.
It means that PQ = BC.
Hence, the triangle ABC is congruent to the triangle DPQ.
(i.e) ∆ ABC ≅ ∆ DPQ.
Thus, by using the AAA criterion for similarity of the triangle, we can say that
∠A = ∠D, ∠B = ∠E and ∠C = ∠F.
To know more about triangle check the below link:
https://brainly.com/question/1058720
#SPJ4
what is the ksp value for baco3(s) if the equilibrium concentration, [ba2 ], is 5.1×10−5 m?
Answers
The Ksp value for BaCO3(s) can be determined using the equilibrium concentration of Ba2+ ions ([Ba2+]) in the solution.
The Ksp (solubility product constant) is a measure of the solubility of a compound in a solution. It is the equilibrium constant for the dissociation of the compound into its constituent ions in a saturated solution.
For the reaction BaCO3(s) ⇌ Ba2+(aq) + \(CO3^2\)-(aq), the Ksp expression is Ksp = [Ba2+][\(CO3^2\)-].
Since the concentration of the carbonate ion ([\(CO3^2\)-]) is not given, we assume that it is in excess and can be considered constant. Therefore, we can express the Ksp value solely in terms of the equilibrium concentration of Ba2+ ions ([Ba2+]).
In this case, the Ksp value is given by Ksp = [Ba2+].
Therefore, the Ksp value for BaCO3(s) is equal to the equilibrium concentration of Ba2+ ions, which is 5.1×\(10^(-5)\) M.
Learn more about Ksp value here:
https://brainly.com/question/25134328
#SPJ11
"Ten less than the quotient of 7 and a number" can be written as:
Answers
Answer:
7 ÷ n - 10
Step-by-step explanation:
"quotient of 7 and a number" can be written as 7 ÷ n
"Ten less than" can be written as -10
So the answer is:
7 ÷ n - 10
I Hope That This Helps! :)
For ax + by = c, solve for x.
Answers
Answer:
Step-by-step explanation:
ax + by = c
ax= c-by <------- Subtract by "by"
x= c-by/a <------ divide by a
what is the slope simplify your answer and write it as a proper fraction , improper fraction or integer

Answers
Answer:
m= 40/29 approximately due to the rise over run
Suppose bob's exam score was at the 80th percentile on an exam whose mean was 90. what was bob's exam score?
Answers
The mean score of 90, and percentile of Bob's score of 80, gives Bob's exam score as approximately 92.5%
What is the formula that gives the exam score from the percentile?The Z-Score of the 80th percentile is 0.8416
The formula for Z-Score is presented as follows;
\(z = \frac{x - \mu}{ \sigma} \)
Where;
\( \sigma = The \: standard \: deviation\)
\( \mu = The \: mean = 90\%\)
x = The given score
Taking the mean as a proportion, we have;
\( \sigma = \sqrt{\frac{\mu \cdot (1-\mu)}{n}}\)
Which gives;
\( \sigma = \sqrt{\frac{0.9 \times (1-0.9)}{100}}= 0.03\)
Therefore, when z = 0.8416, gives;
\(0.8416 = \frac{x - 0.9}{ 0.03} \)
x = 0.8416 × 0.03 + 0.9 ≈ 0.925
Therefore;
Bob's exam score is approximately 92.5%Learn more about Z-Score here:
https://brainly.com/question/25638875
#SPJ4
How many simple random samples of size 3 can be selected from a population of size 7.
Answers
By using combination, it can be obtained that
Number of simple random samples of size 3 that can be selected from a population of size 7 = 35
What is combination?
Combination determines the number of arrangements that can be made from a collection of objects when the order of arrangement is not taken into account.
Here, concept of combination is used
Number of simple random samples of size 3 that can be selected from a population of size 7 = \({7 \choose 3}\) = 35
To learn more about combination, refer to the link-
https://brainly.com/question/11732255
#SPJ1
These box plots show the basketball scores for two teams.
Which statement is the most appropriate comparison of the spreads?

Answers
Answer: The interquartile range (1QR) for the Bulldogs, 20, is less than the IQR for the Wolverines , 30.
Step-by-step explanation:
will mark brain list
A. 30cm2
B.32cm2
C. 22cm2
D.44cm2

Answers
consider the function f(x)=x−3x 1. (a) find the domain of f(x).
Answers
The domain of the function f(x) = x - 3x^1 is all real numbers except for 0.What is a domain?The domain is a set of values for which a function is defined.
The function's output is always dependent on the input provided in the domain. In mathematics, the domain of a function f is the set of all conceivable input values (often the "x" values).In order to obtain the domain of f(x) = x - 3x^1, we need to consider what input values are not allowed to be used, because these input values would result in a division by zero. The value x^1 in this equation represents the same thing as x. Thus, the function can be written as f(x) = x - 3x. f(x) = x - 3x = x(1 - 3) = -2x.Therefore, the domain of f(x) is all real numbers, except for zero. We cannot divide any real number by zero.
To know more about function , visit;
https://brainly.com/question/11624077
#SPJ11
The graph shows the linear relationship between the maximum area in square feet that
can be painted and the number of gallons of paint used.
Paint Coverage
1,800
1,600
1,400
1,200
1,000
800
3 600
400
200
0
1 2 3
Number of Gallons of Paint
Which of these best represents the rate of change of the maximum area painted with
respect to the number of gallons of paint used?
Answers
Answer: 400 ft ^2 / gal
Step-by-step explanation: rise over run
describe and correct the error in graphing the function y = x - 1 with the domain 1 , 2 , 3 ,4 ,and 5

Answers
The graph of the function is y - 1 = x, not y = x - 1.
What is a graph?The set of ordered pairings (x, y) where f(x) = y makes up the graph of a function.
These pairs are Cartesian coordinates of points in two-dimensional space and so constitute a subset of this plane in the general case when f(x) are real values.
Given, y = (x - 1).
When x = 1, y = 0 ⇒ (1, 0).
When x = 2, y = 1 ⇒ (2, 1).
When x = 3, y = 2 ⇒ (3, 2).
When x = 4, y = 3 ⇒ (4, 3).
When x = 5, y = 4 ⇒ (5, 4)
learn more about graphs here :
https://brainly.com/question/2288321
#SPJ1
Drag each expression to an equivalent form.

Answers
The result of the given exponential expression is given as 1/8, 3^2, 1/5 and 5^-2
Properties of exponentsSome of the properties of exponents are expressed as shown below;
1) a^-n = 1/a^n
In order to answer the given questions, we will use the following properties above;
3^-4 = 1/3^4 where a is equivalent to 3 and n is equivalent to 4
Similarly;
1/2^3 = 2^-3 = 1/8
For the expression 1/3^-2
1/3^-2 = 1/(1/3^2)
1/3^-2 = 3^2
For the expression 5^-1
5^-1 = 1/5^1
5^-1 = 1/5
Also for 1/5^2
1/5^2 = 1/25 = 5^-2
Hence the result of the given exponential expression is given as 1/8, 3^2, 1/5 and 5^-2
Learn more on exponent here: https://brainly.com/question/11975096
#SPJ1
Help
-
O
O
O
I
I
I
I
I
I
I
I
I
O

Answers
The required function is f(x) = \(\sqrt[3]{x-8}\) +3.
Given the curve of the function represented on the x-y plane.
To find the required function, consider the point on the curve and check which function satisfies it.
Let P1(x, f(x)) be any point on the curve and P2(0, 1).
1. f(x) = \(\sqrt[3]{x-8}\) +3
To check whether P2(0, 2) satisfies the equation by substitute x = 0 in the equation and check whether f(0) = 1.
f(0) = \(\sqrt[3]{0-8}\) +3.
f(0) = \(\sqrt[3]{-8}\) + 3.
f(0) = -2 + 3
f(0) = 1
This is the required function.
2. f(x) = \(\sqrt[3]{x - 3}\) +8
To check whether P2(0, 2) satisfies the equation by substitute x = 0 in the equation and check whether f(0) = 1.
f(0) = \(\sqrt[3]{0 - 3}\) + 8.
f(0) = \(\sqrt[3]{-3}\) + 8.
f(0) = \(\sqrt[3]{-3}\) + 8 ≠ 1
This is not a required function.
3. f(x) = \(\sqrt[3]{x + 3}\) +8
To check whether P2(0, 2) satisfies the equation by substitute x = 0 in the equation and check whether f(0) = 1.
f(0) = \(\sqrt[3]{0 + 3}\) + 8.
f(0) = \(\sqrt[3]{3}\) + 8.
f(0) = \(\sqrt[3]{3}\) + 8 ≠ 1
This is not a required function.
4. f(x) = \(\sqrt[3]{x+8}\) +3
To check whether P2(0, 2) satisfies the equation by substitute x = 0 in the equation and check whether f(0) = 1.
f(0) = \(\sqrt[3]{0+8}\) +3.
f(0) = \(\sqrt[3]{8}\) + 3.
f(0) = 2 + 3
f(0) = 5 ≠ 1
This is not a required function.
Hence, the required function is f(x) = \(\sqrt[3]{x-8}\) +3.
Learn more about function click here:
https://brainly.com/question/32429136
#SPJ1
Plot the solutions. Irrespective of the chosen initial approximation, the Picard iterates seem to converge, why? Hint: For (c), approximate cos x by taking appropriate number of terms of its Taylor series.
Answers
The accuracy of this approximation depends on the number of terms included in the series and the value of x. For x close to zero, a few terms may be sufficient to obtain a good approximation.
Without any specific equation or initial conditions given, it is not possible to plot the solutions or find Picard iterates. However, I can explain why Picard iteration method works for most initial approximations.
The Picard iteration method is an iterative numerical method used to approximate solutions to initial value problems of the form y' = f(x,y), y(x0) = y0. It involves constructing a sequence of functions yn(x) that converges to the solution y(x) as n approaches infinity. The nth iterate is given by:
yn+1(x) = y0 + ∫x0xf(t, yn(t)) dt
where y0 is the initial approximation, and the integral is taken over the interval [x0,x].
The reason why Picard iteration method usually converges for most initial approximations is due to the contraction mapping principle. If the function f(x,y) satisfies the Lipschitz condition with respect to y, i.e. there exists a constant L such that |f(x,y1) - f(x,y2)| ≤ L|y1 - y2| for all x, y1, y2, then the Picard iterates converge uniformly to the solution y(x).
The Lipschitz condition ensures that the mapping from yn to yn+1 is a contraction, which means that the distance between two consecutive iterates decreases with each iteration. This guarantees convergence of the sequence of iterates to the unique fixed point of the mapping, which is the solution to the initial value problem.
As for part (c), one can use the Taylor series expansion of cos(x) to approximate it for small values of x:
\(cos(x) ≈ 1 - x^2/2! + x^4/4! - x^6/6!\)
Learn more about initial approximation,
https://brainly.com/question/29418238
#SPJ4
please help (picture) 25 points

Answers
Answer:
1) perimeter = sum of all the sides = 3y+9+2y+4+y+3+2y+4 = 8y+20
2) P = 4(5x-2) = 20x-8