Write the equation for the equation below. The variable should be on the left
side. Do not enter any spaces.
PLEASE HELPP !!

Answers
Related Questions
Can you find out what X equals.

Answers
Step-by-step explanation:
Pythagoras theorem may be used :
as we can see pq iS perpendicular on oq
OQ²+pq² = op²
x² + (9)² = (3)²
x²+81= 9
x² = 81-9
x²= 72
x = √72
x = 8.48528137 ✓
Answer:
Step-by-step explanation:
OQ²+pq² = op²
x² + (9)² = (3+x)²
x²+81= 9+ 6x +\(x^{2}\)
6x=72
x=12
A piece of aluminum occupies a volume of 12.7 milliliters and weighs 87.3 grams. What is its density of the aluminum rounded to the nearest hundredth? Only enter numerical values, which can include a decimal point.
Answers
Answer:
6.87 g/mL
Step-by-step explanation:
The density of an object can be found by dividing the mass by the volume.
\(density=\frac{mass}{volume}\\\\ d=\frac{m}{ v}\)
We know that the aluminum occupies a volume of 12.7 milliliters and weighs 87.3 grams. Therefore, the mass is 87.3 g and the volume is 12.7 mL.
\(m= 87.3 g\\\\v=12.7 mL\)
Substitute the values into the formula.
\(d= \frac{87.3 g}{12.7 mL}\)
Divide 87.3 g by 12.7 mL
\(d=6.87401575 g/mL\)
Round to the nearest hundredth. The 4 in the thousandth place tells us to leave the 7 in the hundredth place.
\(d= 6.87 g/mL\)
The density of the aluminum is about 6.87 grams per milliliter.
WILL MAKE BRAINLEST PLS HELP

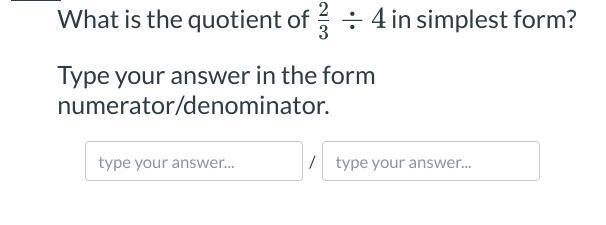
Answers
SHOPPING Ramos went to a pizza shop and spent half of
his money on lunch. If Ramos had $4.50 left after lunch,
how much money did he have originally?
EE
THE
HELSE
TELEP
Help i need it quick
Answers
assume x and y are functions of t. evaluate for the following. y³=2x²+14; dx/dt =3,x=5, y=4
dy/dt = __ (Round to two decimal places as needed.)
Answers
To evaluate dy/dt given the equation y³ = 2x² + 14, along with dx/dt = 3, x = 5, and y = 4, we can use implicit differentiation and substitute the given values.
dy/dt is approximately equal to 0.51 (rounded to two decimal places).
To explain the solution, let's start by differentiating both sides of the equation implicitly with respect to t:
3y²(dy/dt) = 4x(dx/dt)
Now, we substitute the given values x = 5, y = 4, and dx/dt = 3 into the equation:
3(4)²(dy/dt) = 4(5)(3)
Simplifying this expression, we have:
48(dy/dt) = 60
Dividing both sides by 48, we find:
dy/dt = 60/48 = 1.25
Therefore, dy/dt is approximately equal to 1.25. Rounded to two decimal places, the value is 0.51.
To learn more about differentiation click here:
brainly.com/question/13958985
#SPJ11
Can someone please help me out with this

Answers
The value of UR = 13 mm
Given:
HGJI ≅ RSTU
proportional sides:
HG = JI
GJ = ST
JI = TU
IH = UR
From the figure:
IH = 13 mm
so IH = UR = 13
UR = 13 mm.
Therefore the value of UR = 13 mm.
Learn more about the value here:
https://brainly.com/question/14316282
#SPJ1
Which graph represents viable values for y = 2x, where x is the number of pounds of rice scooped and purchased from a bulk bin at the grocery store and y is the total cost of the rice? On a coordinate plane, a straight line with a positive slope begins at point (0, 0), and ends at point (2.5, 5). On a coordinate plane, blue diamonds appear at points (0, 0), (1, 2), (2, 4). On a coordinate plane, a straight line with a positive slope begins at point (negative 2.5, negative 5), crosses the x- and y-axis at point (0, 0), and ends at point (2.5, 5). On a coordinate plane, blue diamonds appear at points (negative 2, negative 4), (negative 1, negative 2), (0, 0), (1, 2), (2, 4).
Answers
Answer: Most Viable: On a coordinate plane, a straight line with a positive slope begins at point (0, 0), and ends at point (2.5, 5).
Also possible, but only if someone scoops exact amounts (maybe pre-packaged for people who don't want to do their own scooping.): On a coordinate plane, blue diamonds appear at points (0, 0), (1, 2), (2, 4).
Step-by-step explanation:
The line beginning at (0,0) ending at (2.5, 5) represents all the prices for any amount that the customer scoops. for example, $5 for 2 1/2 pounds or $1 for 1/2 pound or $2 for 1 pound would all be represented in the graphed line.
The graphs with negative values don't make sense. You can't scoop negative pounds!
Again, good descriptions but difficult to sort out. Are you able to hit [enter] or [return] between options, or attach a screenshot?
A scientist counts the number of inclusions in a sample of 30 tourmaline rocks, each of weight 50g. a If the sample mean number of inclusions per gem is 31.0635 and the sample standard deviation of the number of inclusions is 2.0996, calculate the standard error of the mean number of inclusions. (Please provide answers rounded to four decimal places) Submit part Score: 0/1 Unanswered b) Use you answer from the previous question to estimate a 95% confidence interval for the mean number of inclusions per tourmaline gem (Please provide your answer to four decimal places).
Answers
a) To calculate the standard error of the mean number of inclusions, we divide the sample standard deviation by the square root of the sample size. In this case, the sample mean number of inclusions is 31.0635, and the sample standard deviation is 2.0996. The sample size is 30. Therefore, the standard error of the mean number of inclusions can be calculated as follows:
Standard Error = Sample Standard Deviation / √Sample Size
Standard Error = 2.0996 / √30 Standard Error ≈ 0.3836 (rounded to four decimal places) b) To estimate a 95% confidence interval for the mean number of inclusions per tourmaline gem, we can use the formula: Confidence Interval = Sample Mean ± (Critical Value × Standard Error) The critical value corresponds to a 95% confidence level, which is 1.96 for a large sample size. Using the standard error calculated in part (a) as 0.3836 and the sample mean of 31.0635, the confidence interval can be calculated as: Confidence Interval = 31.0635 ± (1.96 × 0.3836)
Confidence Interval ≈ 31.0635 ± 0.7521 Confidence Interval ≈ (30.3114, 31.8156) (rounded to four decimal places) Therefore, we can estimate with 95% confidence that the mean number of inclusions per tourmaline gem lies between approximately 30.3114 and 31.8156.
Learn more about The critical value here: brainly.com/question/33533143
#SPJ11
Use the Slope Formula to calculate the slope of a line with these two points. Find the slope of the line that passes through (1, 9) and (8, 8).
Answers
\((\stackrel{x_1}{1}~,~\stackrel{y_1}{9})\qquad (\stackrel{x_2}{8}~,~\stackrel{y_2}{8}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{9}}}{\underset{\textit{\large run}} {\underset{x_2}{8}-\underset{x_1}{1}}} \implies \cfrac{ -1 }{ 7 } \implies - \cfrac{1 }{ 7 }\)
If x+4/4 = y+7/7 then x/4 =___.
(Number 9 is the one I need an answer for)

Answers
Answer:
4th answer is correct
Step-by-step explanation:
First, let us make x the subject.
\(\sf \frac{x+4}{4} =\frac{y+7}{7}\)
Use cross multiplication.
\(\sf 7(x+4)=4(y+7)\)
Solve the brackets.
\(\sf 7x+28=4y+28\)
Subtract 28 from both sides.
\(\sf 7x=4y+28-28\\\\\sf7x=4y\)
Divide both sides by 7.
\(\sf x=\frac{4y}{7}\)
Now let us find the value of x/4.
To find that, replace x with (4y/7).
Let us find it now.
\(\sf \frac{x}{4} =\frac{\frac{4y}{7} }{4} \\\\\sf \frac{x}{4} =\frac{4y}{7}*\frac{1}{4} \\\\\sf \frac{x}{4} =\frac{4y}{28}\\\\\sf \frac{x}{4} =\frac{y}{7}\)
in mathematics to ______means to replace an expression with one that is equivalent to it
plzz need ans
Answers
Answer:
I believe the answer is substitution
Step-by-step explanation:
Hope this Helps :)
i think its called a regular expression.. but i'm not 100% sure. Sorry if im wrong.
Evaluate the limit
\(\rm\displaystyle\lim_{\rm x\to 4}\left(\frac{\sqrt{\rm x}-\sqrt{3\sqrt{\rm x}-2}}{\rm x^2-16}\right)=\ldots\)
Answers
We are given with a limit and we need to find it's value so let's start !!!!
\({\quad \qquad \blacktriangleright \blacktriangleright \displaystyle \sf \lim_{x\to 4}\dfrac{\sqrt{x}-\sqrt{3\sqrt{x}-2}}{x^{2}-16}}\)
But , before starting , let's recall an identity which is the main key to answer this question
\({\boxed{\bf{a^{2}-b^{2}=(a+b)(a-b)}}}\)Consider The limit ;
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{\sqrt{x}-\sqrt{3\sqrt{x}-2}}{x^{2}-16}}\)
Now as directly putting the limit will lead to indeterminate form 0/0. So , Rationalizing the numerator i.e multiplying both numerator and denominator by the conjugate of numerator
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{\sqrt{x}-\sqrt{3\sqrt{x}-2}}{x^{2}-16}\times \dfrac{\sqrt{x}+\sqrt{3\sqrt{x}-2}}{\sqrt{x}+\sqrt{3\sqrt{x}-2}}}\)
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{(\sqrt{x}-\sqrt{3\sqrt{x}-2})(\sqrt{x}+\sqrt{3\sqrt{x}-2})}{(x^{2}-4^{2})(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
Using the above algebraic identity ;
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{(\sqrt{x})^{2}-(\sqrt{3\sqrt{x}-2})^{2}}{(x-4)(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{x-(3\sqrt{x}-2)}{(x-4)(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{x-3\sqrt{x}+2}{\{(\sqrt{x})^{2}-2^{2}\}(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{x-3\sqrt{x}-2}{(\sqrt{x}-2)(\sqrt{x}+2)(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
Now , here we need to eliminate (√x-2) from the denominator somehow , or the limit will again be indeterminate ,so if you think carefully as I thought after seeing the question i.e what if we add 4 and subtract 4 in numerator ? So let's try !
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{x-3\sqrt{x}-2+4-4}{(\sqrt{x}-2)(\sqrt{x}+2)(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{(x-4)+2+4-3\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
Now , using the same above identity ;
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{(\sqrt{x}-2)(\sqrt{x}+2)+6-3\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{(\sqrt{x}-2)(\sqrt{x}+2)+3(2-\sqrt{x})}{(\sqrt{x}-2)(\sqrt{x}+2)(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
Now , take minus sign common in numerator from 2nd term , so that we can take (√x-2) common from both terms
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{(\sqrt{x}-2)(\sqrt{x}+2)-3(\sqrt{x}-2)}{(\sqrt{x}-2)(\sqrt{x}+2)(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
Now , take (√x-2) common in numerator ;
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{(\sqrt{x}-2)\{(\sqrt{x}+2)-3\}}{(\sqrt{x}-2)(\sqrt{x}+2)(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
Cancelling the radical that makes our limit again and again indeterminate ;
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{\cancel{(\sqrt{x}-2)}\{(\sqrt{x}+2)-3\}}{\cancel{(\sqrt{x}-2)}(\sqrt{x}+2)(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{(\sqrt{x}+2-3)}{(\sqrt{x}+2)(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
\({:\implies \quad \displaystyle \sf \lim_{x\to 4}\dfrac{(\sqrt{x}-1)}{(\sqrt{x}+2)(x+4)(\sqrt{x}+\sqrt{3\sqrt{x}-2})}}\)
Now , putting the limit ;
\({:\implies \quad \sf \dfrac{\sqrt{4}-1}{(\sqrt{4}+2)(4+4)(\sqrt{4}+\sqrt{3\sqrt{4}-2})}}\)
\({:\implies \quad \sf \dfrac{2-1}{(2+2)(4+4)(2+\sqrt{3\times 2-2})}}\)
\({:\implies \quad \sf \dfrac{1}{(4)(8)(2+\sqrt{6-2})}}\)
\({:\implies \quad \sf \dfrac{1}{(4)(8)(2+\sqrt{4})}}\)
\({:\implies \quad \sf \dfrac{1}{(4)(8)(2+2)}}\)
\({:\implies \quad \sf \dfrac{1}{(4)(8)(4)}}\)
\({:\implies \quad \sf \dfrac{1}{128}}\)
\({:\implies \quad \bf \therefore \underline{\underline{\displaystyle \bf \lim_{x\to 4}\dfrac{\sqrt{x}-\sqrt{3\sqrt{x}-2}}{x^{2}-16}=\dfrac{1}{128}}}}\)
We can transform the limand into a proper rational expression by substitution.
Let y = √x. Then as x approaches 4, y will approach √4 = 2. So
\(\displaystyle \lim_{x\to4}\frac{\sqrt x - \sqrt{3 \sqrt x - 2}}{x^2 - 16} = \lim_{y\to2} \frac{y - \sqrt{3y-2}}{y^4 - 16}\)
Now let z = √(3y - 2). Then as y approaches 2, z will approach √(3•2 - 2) = 2 as well. It follows that y = (z² + 2)/3, so that
\(\displaystyle \lim_{y\to2} \frac{y - \sqrt{3y-2}}{y^4-16} = \lim_{z\to2} \frac{\frac{z^2+2}3 - z}{\frac{(z^2+2)^4}{81}-16} \\\\ = \lim_{z\to2} \frac{27(z^2+2)-81z}{(z^2+2)^4 - 1296} \\\\ = 27 \lim_{z\to2} \frac{z^2 - 3z + 2}{z^8 + 8z^6 + 24z^4 + 32z^2 - 1280}\)
Plugging z = 2 into the denominator returns a value of 0, which means z - 2 divides z⁸ + 8z⁶ + 24z⁴ + 32z² - 1280 exactly. Polynomial division shows that
\(\dfrac{z^8 + 8z^6 + 24z^4 + 32z^2 - 1280}{z-2} \\\\ = z^7+2z^6+12z^5+24z^4+72z^3+144z^2+320z+640\)
and it's easy to see that the numerator is also divisible by z - 2, since
\(z^2 - 3z + 2 = (z - 1) (z - 2)\)
So, we can eliminate the factor of z - 2 and we're left with
\(\displaystyle 27 \lim_{z\to2} \frac{z^2 - 3z + 2}{z^8 + 8z^6 + 24z^4 + 32z^2 - 1280} = 27 \lim_{z\to2}\frac{z-1}{z^7+\cdots+640}\)
The remaining limand is continuous at z = 2, so we can evaluate the limit by direct substitution:
\(\displaystyle 27 \lim_{z\to2}\frac{z-1}{z^7+\cdots+640} = \frac{27}{3456} = \boxed{\frac1{128}}\)
The table below shows the probability distribution of the random variable X.
What is the expected value of X?
x 0 1 2 3
P(X=x) 0.3 a 0.2 0.1

Answers
Based on the given parameters, the expected value of x is 1.1
How to determine the expected value of x?The table of values is given as
x 0 1 2 3
P(X=x) 0.3 a 0.2 0.1
The sum of probabilities is 1
So, we have
0.3 + a + 0.2 + 0.1 = 1
This gives
0.6 + a = 1
Evaluate
a = 0.4
The expected value of x is calculated as
E(x) = Sum of (x * P(x))
So, we have
E(x) = 0 * 0.3 + 1 * a + 2 * 0.2 + 3 * 0.1
This gives
E(x) = 0 * 0.3 + 1 * 0.4 + 2 * 0.2 + 3 * 0.1
Evaluate
E(x) = 1.1
Hence, the expected value of x is 1.1
Read more about expected value at
https://brainly.com/question/15858152
#SPJ1
PLS HELP ASAP (Brainliest answer if it's right)
The width of a rectangle measures (8p+5) centimeters, and its length measures (4p+4) centimeters. Which expression represents the perimeter, in centimeters, of the rectangle?
1. 24p+18
2. 8+13p
3. 9+12p
4. 26p+16
Thx if u help>3
Answers
Answer:
1. 24p + 18
Step-by-step explanation:
One of the formulas used to find the perimeter of a rectangle is:
P = 2(l + w)
Where P is the perimeter, l is the length, and w is the width. We can substitute in the given values:
P = 2[(4p + 4) + (8p + 5)]
Now we can combine the like terms:
P = 2[12p + 9]
And simplify:
P = 24p + 18
This is the same as option 1.
factorise the quadratic equation x^2 + 14 + 48 hence solve the quadratic equation x^2 + 14 + 48 = 0
Answers
Answer:
(x+6) (x+8)
Step-by-step explanation:
x² + 14x + 48 = 0
ac = 48
b = 14
(x + 6) (x + 8)
Thus, x= -6, x = -8
Can someone help me find an equation for both of these ❤️

Answers
Answer and Step-by-step explanation:
First equation:
y = -4x + 9
This equation has a negative slope (a slope that does downwards) and has a positive y-intercept (at (0, 9)).
Second Equation:
y = -4x - 4
This equation is parallel to the first line because it has the same slope. It also has a negative y-intercept (at (0, -4)).
#teamtrees #PAW (Plant And Water)
at a party there are only single women and married men with their wives. the probability that a randomly selected woman is single is $\frac{2}{5}$. what fraction of the people in the room are married men?
Answers
60% of the people in the room are married men.
We can use the information that the probability of a randomly selected woman being single is 2/5 to find the fraction of people in the room who are married men.
Let's call the fraction of people in the room who are married men x. The fraction of people in the room who are single women is (2/5) and the fraction of people in the room who are married men and their wives is (1-x)
Since there are only single women and married men with their wives at the party, we know that the sum of the fractions of single women and married men and their wives must be 1.
(2/5) + (1-x) = 1
We can solve this equation for x:
x = 1 - (2/5) = 3/5
So the fraction of people in the room who are married men is 3/5 or 0.6
So, 60% of the people in the room are married men.
Learn more about probability:
https://brainly.com/question/30034780
#SPJ4
what is the third stage of the rational model of decision making?
Answers
The temperature was -3, 0, 2, -1, and -3 on five consecutive days. What was the average temperature for those five days?
Answers
Answer:
-1 degrees
Step-by-step explanation:
The average = sum of all values/# of values = sum of all temperatures/# of days=
(-3+0+2-1-3)/5= -1
a bag contains 16 black balls and 14 white balls. two balls are drawn at random from the bag, one after the other without replacement. what is the joint probability the first ball drawn was black and the second ball drawn was also black?
Answers
Answer:
Step-by-step explanation:
What is the equation of the line that passes through the point (7,-3) and has an undefined slope?
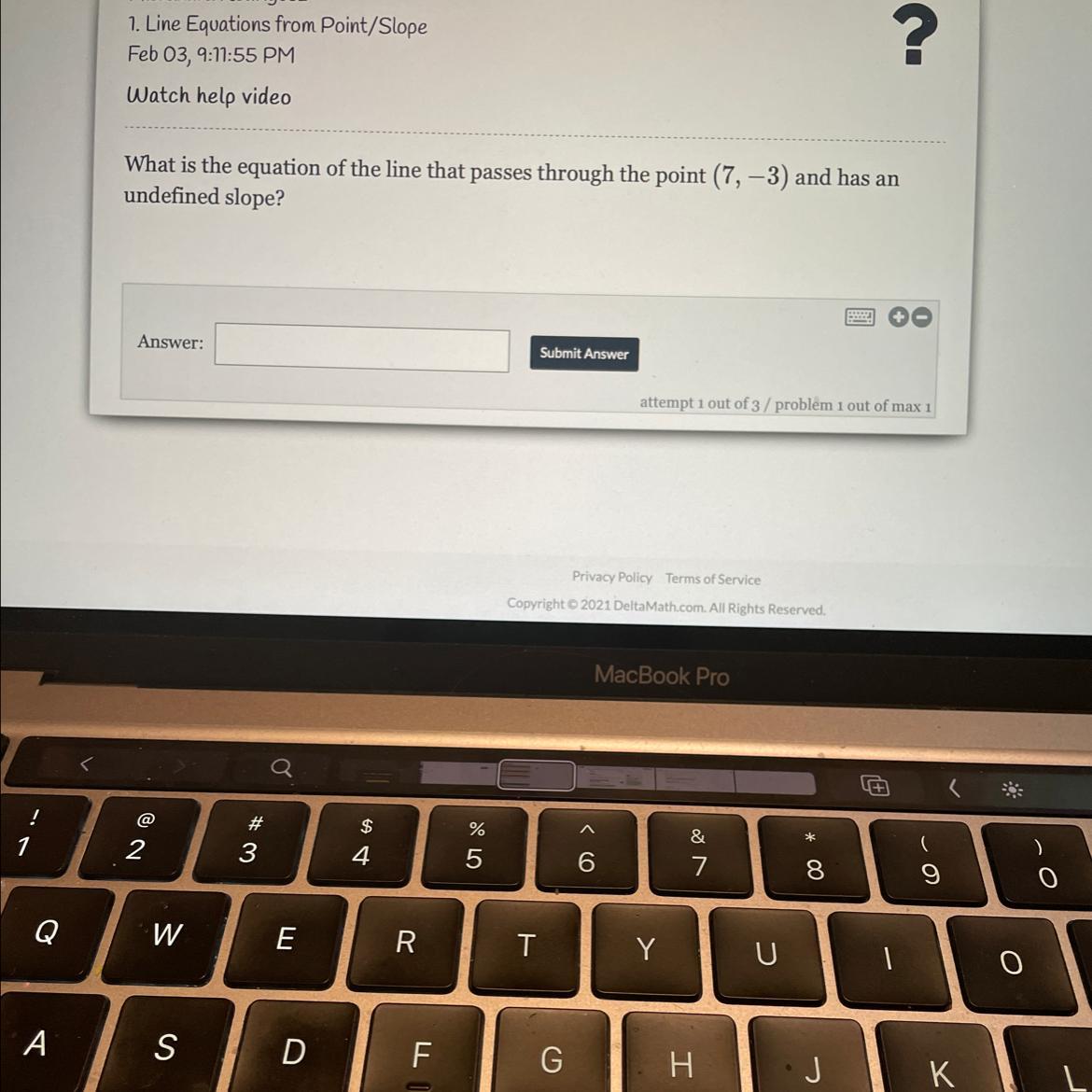
Answers
Answer:
x=7
Step-by-step explanation:
Answer:
x = 7
Step-by-step explanation:
A line with undefined slope is a vertical line. A vertical line has the equation
x = anumber
The point you were given has an x and a y...(x,y) The first number is the x.
x = 7
That's it, thats the equation of a line with undefined slope that goes through (7, -3).
<<<Fun fact: Lines with 0 slope are horizontal lines and have the equation
y = anumber >>>
please help, thank you!!

Answers
Answer:
Coordinates of M and N are
(-3, -2.5) and (3, -1)
The order is not important since we are not told where M and N points actually are. The attached graph will make this clear
Step-by-step explanation:
The two equations are
\(4y=x-7 \textrm{\space ( Eq 1)}\)
and
\(x^2 + xy = 4 + 2y^2 \textrm{ (Eq 2)}\)
Adding 7 to both sides of Eq 1 gives us
\(x = 4y + 7\)
Eq2 can be re-written as
\(x^2 + xy - 4 - 2y^2 = 0 \textrm{ (Eq 3)}\)
The above is done by subtracting \(4 + 2y^2\) on both sides of Eq 2
Substituting for \(x = 4y + 7\) in Eq 3 gives us
\(\left(4y+7\right)^2+\left(4y+7\right)y-4-2y^2 = 0\)
Let's examine the first two terms and simplify
\((4y+7)^2 = \left(4y\right)^2+2\cdot \:4y\cdot \:7+7^2\) = \(16y^2+56y+49\) (A)
\(\left(4y+7\right)y = 4y^2 + 7y\) (B)
So Eq 3 can be reduced to a quadratic equation with one variable, \(y\)
(A) + (B) - \(4 -2y^2\) = \(6y^2+56y+49+4y^2+7y-4-2y^2\)
Grouping like terms we get
\(16y^2+4y^2-2y^2+56y+7y+49-4\)
Adding similar terms we get
\(18y^2+63y+45 = 0\)
We can divide both sides of the equation by 9 to make it easier to solve using the equation for the solutions of a quadratic equation
Dividing both sides by 9 we get
\(2y^2+7y+5 = 0\)
Use the quadratic formula
\(y_1, y_2 = \dfrac{ -b \pm \sqrt{b^2 - 4ac}}{ 2a }\)
where a is the coefficient of \(y^2\), \(b\) the coefficient of \(y\) and \(c\) the constant
Here \(a = 2, b = 7\) and \(c = 5\)
So we get
\(y_1, y_2 = \frac{-7\pm \sqrt{7^2-4\cdot \:2\cdot \:5}}{2\cdot \:2}\) = \(\frac{-7\pm \:3}{2\cdot \:2}\)
The above is obtained by noting that
\(\sqrt{7^2-4\cdot \:2\cdot \:5}} = \sqrt{49-40} =\sqrt{9} = 3\)
\(y_1=\frac{-7+3}{2\cdot \:2},\:y_2=\frac{-7-3}{2\cdot \:2}\)
\(y_1 = \frac{-7+3}{2\cdot \:2} = \frac{-4}{4} = -1\) (using the + component)
\(y_2 = \frac{-7-3}{2\cdot \:2} = \frac{-10}{4} = -2.5\)
Find \(x_1\) and \(x_2\) by substituting each of these values in the equation for \(x\)
\(x_1 = 4(-1) + 7 = -4 + 7 = 3\)
Therefore the coordinates of M and N are
\((-3, -2.5)\) and \((3, -1)\)
The order is not important since we are not told which are M and N points. See the attached graph for a visual depiction
Hope that helps :)

Answer:
\(\sf M =\left(-3, -\dfrac{5}{2}\right), \quad N= \left(3, -1 \right)\)
Step-by-step explanation:
Given:
\(\begin{cases}4y = x - 7\\x^2+xy=4+2y^2\end{cases}\)
To find the points at which the line and the curve intersect, rewrite the first equation to make y the subject by dividing both sides by 4:
\(\implies y=\dfrac{1}{4}x-\dfrac{7}{4}\)
Substitute the expression for y into the second equation and solve for x:
\(\implies x^2+x\left(\dfrac{1}{4}x-\dfrac{7}{4}\right)=4+2\left(\dfrac{1}{4}x-\dfrac{7}{4}\right)^2\)
\(\implies x^2+\dfrac{1}{4}x^2-\dfrac{7}{4}x=4+2\left(\dfrac{1}{16}x^2-\dfrac{7}{8}x+\dfrac{49}{16}\right)\)
\(\implies \dfrac{5}{4}x^2-\dfrac{7}{4}x=4+\dfrac{1}{8}x^2-\dfrac{7}{4}x+\dfrac{49}{8}\)
\(\implies \dfrac{5}{4}x^2-\dfrac{7}{4}x=\dfrac{1}{8}x^2-\dfrac{7}{4}x+\dfrac{81}{8}\)
\(\implies \dfrac{5}{4}x^2=\dfrac{1}{8}x^2+\dfrac{81}{8}\)
Multiply both sides by 8:
\(\implies 10x^2=x^2+81\)
\(\implies 9x^2=81\)
\(\implies x^2=9\)
\(\implies x=\sqrt{9}\)
\(\implies x=\pm3\)
To find the y-values of the coordinates of the points of intersection (M and N), substitute the found values of x into the expression for y:
\(x=3 \implies y=\dfrac{1}{4}(3)-\dfrac{7}{4}=-1\)
\(x=-3 \implies y=\dfrac{1}{4}(-3)-\dfrac{7}{4}=-\dfrac{5}{2}\)
Therefore:
\(\sf M =\left(-3, -\dfrac{5}{2}\right), \quad N= \left(3, -1 \right)\)
Write an expression to describe the relationship of the data in this table

Answers
The relationship of the data in this table can be described as c = 21 * t.
What is a data table?
A data table is a way to express information in a tabular form. A data table has rows as the horizontal blocks and columns as the vertical blocks. For e.g. a data table of a school administration has the information of students along with their admission numbers, roll numbers, class, sections, and subjects.
Let us consider the given question for an advisor who pays every day for their ads on a site/page. The table clearly shows that the cost paid for advertisements in a day is $21. Similarly the cost for 3 days and 6 days is$63 and $126 respectively. Now, it is clear that that if c is the cost for the time taken t, then the total cost c is given by:c= 21 * t
Therefore, the relationship of the data in the given table is c = 21 * t.
Learn more about data table from the given link
https://brainly.com/question/27982562
#SPJ1
while logistic regression and classification and regression trees (cart) have the same end goal, each model approaches the goal in a different way. discuss the differences in the two models. provide a specific example of a situation where employing a cart model would be preferable to a logistic regression model. explain what makes the cart model superior in your example.
Answers
Logistic regression models the probability of a binary outcome, while CART models segment data into categories. For example, CART is preferable when data has complex interactions, as it can partition data into multiple categories.
Logistic regression and classification and regression trees (CART) are two different machine learning models used for binary classification problems. Logistic regression models the probability of one class or the other based on a linear combination of input variables. This makes it useful for predicting a binary outcome, such as whether a customer will purchase a product or not. On the other hand, CART is a decision tree model that divides data into categories. It uses a tree-like structure to split the data into segments based on the input features. This makes it useful for dealing with data with complex interactions, as it can partition data into multiple categories. For example, a CART model would be preferable to a logistic regression model if there are multiple underlying factors that affect the binary outcome. In this case, a CART model could more accurately identify the categories that are associated with a particular outcome. Overall, CART models are superior for dealing with data with complex interactions, whereas logistic regression is better for simpler data.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
Suppose Joan has a fair four-sided die with sides that are numbered 1, 2, 3, and 4.
After she rolls it 20 times, how many times does she roll the number 3?
A. 3
B. 5
C. 6
D. It is impossible to tell.
Answers
To find the expected number of times Joan rolls a 3, we use the formula for mean of a binomial distribution.
The correct option is, option (C) 6.
The probability of rolling a number 3 on any given roll is 1/4
If Joan rolls the die 20 times, the number of times she rolls a 3 will follow a binomial distribution with n = 20 (number of trials) and p = 1/4 (probability of success).
The formula for the probability mass function of a binomial distribution is:
P(X=k) = (n choose k) * p^k * (1-p)^(n-k)
where X is the random variable representing the number of successes (the number of times Joan rolls a 3), k is the number of successes, n is the number of trials, p is the probability of success, and (n choose k) is the binomial coefficient, which represents the number of ways to choose k items from a set of n items.
Using this formula, we can calculate the probability of rolling a 3 exactly k times out of 20 rolls:
P(X=k) = (20 choose k) * (1/4)^k * (3/4)^(20-k)
To find the expected number of times Joan rolls a 3, we can use the formula for the mean of a binomial distribution:
E(X) = n * p
In this case, E(X) = 20 * 1/4 = 5
Therefore, the expected number of times Joan rolls a 3 is 5.
Since the possible answers are integers, the closest answer to 5 is 6. Therefore, the answer is (C) 6.
Know more about binomial distribution here:
https://brainly.com/question/29163389
#SPJ11
What is the result when the number 36 is decreased by 25%
Answers
Answer:
27
Step-by-step explanation:
1. 100% - 25% = 75%
2). 3/4 x 36 = 27
Answer:
27
Step-by-step explanation:
There are 2 ways we can solve this:
The first way is with percents:
100%-25%=75%
75/100=0.75 or 3/4
3/4·36
27
The second way is to use common knowledge:
We know that 25% is 1/4 of anything. So, 1/4 of 36 is 9.
36-9=27
Hope this helps! :)
5. For the following function, evaluate f(5)-f(4), *
f(x) = -2x²-x+3

Answers
For this following function by evaluating f(5)-f(4) we get -19.
What is evaluate?
Finding the value of an algebraic expression when a given number is used to replace a variable is known as evaluating the expression. When evaluating an expression, we change the variable in the expression to the given number and then use the order of operations to simplify the expression.
Sol- f(5)-f(4)
f(5)-f(4)= (-2.5^2-5+3)-(-2.4^2-4+3)
Calculate the power
(-2×25-5+3)-(-2×4^2-4+3)
Calculate the product or quotient
(-50-5+3)-(-2×16-4+3)
Calculate the sum
-52-(-32-4+3)
=-52-(-33)
determine the sign
=-52+33
By calculating the sum of difference we are get
-19.
To know more about evaluate click-
https://brainly.com/question/25907410
#SPJ13
please help!!!!
pic below
.................

Answers
Answer:
GCF = greatest common factor
LCM = least common multiple
prime number = 5
factor = a number to be multiplied
composite number = 6
Solve x2 + 2x + 7 = 0 using the quadratic formula. Select all solutions that apply.
Answers
Solving the equation x²+2x+7 using the quadratic formula, the resultant answer is x = -1 ± 2.44949i.
What is the quadratic formula?Any quadratic problem can be solved using the quadratic formula.
The equation is first changed to have the form ax²+bx+c=0, where a, b, and c are coefficients.
After that, we enter these coefficients into the following formula:
(-b±√(b²-4ac))/(2a)
Quadratic equations can be solved using one of three main strategies: factoring, the quadratic formula, or completing the square.
So, solving x²+2x+7 using the quadratic formula as follows:
Quadratic formula: (-b±√(b²-4ac))/(2a)
Substitute values and caluclate:
x = (-b±√(b²-4ac))/(2a)
x = (-2±√(2²-4(1)(7))/(2*1)
x = (-2±√4-28)/(2)
x = (-2±√-24)/(2)
Complex roots:
x = (-2±2√6i)/(2)
x = -2/2 ± 2√6i/2
Simplifying fractions:
x = -1 ± √6i
So, we have:
x = -1 ± 2.44949i
Therefore, solving the equation x²+2x+7 using the quadratic formula, the resultant answer is x = -1 ± 2.44949i.
Know more about the quadratic formula here:
https://brainly.com/question/1214333
#SPJ4
Copy the axes below.
By first filling in the table for y = 3x - 5, draw the
graph of y = 3x - 5 on your axes.
X
Y
-
-2
-1
-8
-
0
-5
1
2
1
Answers
The line represents the graph of the equation y = 3x - 5.
The graph of y = 3x - 5 using the given table of values.
To draw the graph, we'll plot the points from the table and then connect them to create a line.
Given table of values:
X Y
-2 -8
-1 -5
0 -5
1 -2
2 1
Now, let's plot these points on the coordinate plane:
Point (-2, -8): This means when x = -2, y = -8. Plot the point (-2, -8) on the graph.
Point (-1, -5): When x = -1, y = -5. Plot the point (-1, -5) on the graph.
Point (0, -5): When x = 0, y = -5. Plot the point (0, -5) on the graph.
Point (1, -2): When x = 1, y = -2. Plot the point (1, -2) on the graph.
Point (2, 1): When x = 2, y = 1. Plot the point (2, 1) on the graph.
After plotting these points, connect them with a straight line. The line represents the graph of the equation y = 3x - 5.
for such more question on graph
https://brainly.com/question/13473114
#SPJ8
