What is the greatest common factor (GCF) of 12 and 30?
Answers
SOLUTION
The given numbers are 12 and 30
Express the numbers as a product of their prime factors
It follows
\(12=2\times2\times3\)and
\(30=2\times3\times5\)From the prime factors
The common factors are
\(2\times3\)Therefore, the greatest common factor is 6
Related Questions
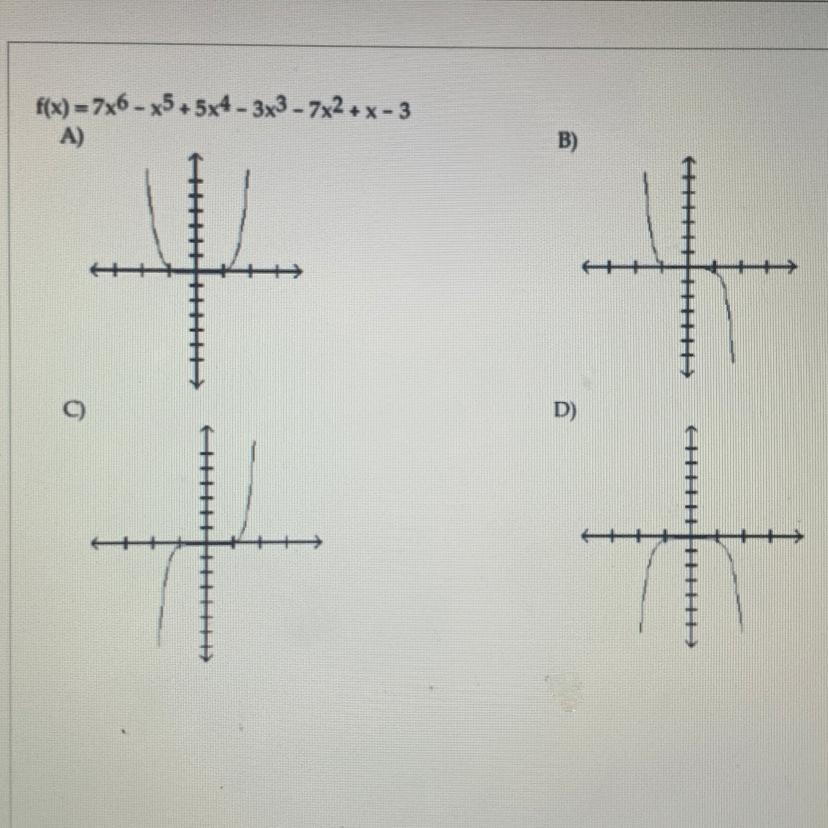
this is for algebra 2
Answers
Answer:
The answer is D
Step-by-step explanation:
Make a table of ordered pairs for the equation.
y=2×+1
Then plot two points to graph the equation.
Answers
-2 -3
-1 -1
0 1
1 3
2 5
i can’t graph it, but i hope this helps
Consider a circle whose equation is x2 + y2 – 2x – 8 = 0. Which statements are true? Select three options. The radius of the circle is 3 units. The center of the circle lies on the x-axis. The center of the circle lies on the y-axis. The standard form of the equation is (x – 1)² + y² = 3. The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.
Answers
We can rewrite the circle equation as:
(x - 1)^2 + y^2 = 9
Then the two true statements are:
"The center of the circle lies on the x-axis"
" The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9."
Which statements are true about the circle?
Remember that a general circle equation with a center (a, b) and radius R is:
(x - a)^2 + (y - b)^2 = R^2
Here the equation is:
x^2 + y^2- 2 x - 8 = 0
We can rewrite this as:
(x^2 - 2x) + y^2 = 8
Adding and subtracting 1 in the left side we can complete squares:
(x^2 - 2x + 1) - 1 + y^2 = 8
(x - 1)^2 + y^2 = 9
Tha is our equation, so the center is (1, 0) and the radius is 3 units.
Then the true statements are:
"The center of the circle lies on the x-axis"
" The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9."
Learn more about circle equations:
https://brainly.com/question/1559324
#SPJ1
find the area of each triangle with the given base and height.
B=10,h=7
Answers
Answer:
the area of the triangle is 35.
Step-by-step explanation:
First you use the formula of the area of a triangle. A = 1/2bh. You plug the base and height in; A = 1/2(10)(7). You multiply these numbers and get 35 as the area.
in a group of 200 people, at least how many have names beginning with the same letter of the alphabet?
Answers
To determine the minimum number of people with names beginning with the same letter of the alphabet in a group of 200 people, we can use the Pigeonhole Principle.
Since there are 26 letters in the alphabet, there are 26 "pigeonholes" or categories for the first letter of a name. If we assume that each person in the group has a different first letter of their name, then we can put one person in each pigeonhole. However, if we add just one more person, there will be at least one pigeonhole with two people in it (since there are only 26 pigeonholes). Therefore, the minimum number of people with names beginning with the same letter of the alphabet in a group of 200 people is 2.
To know more about Pigeonhole visit:
https://brainly.com/question/30319732
#SPJ11
List a, b, and c for the following Quadratic: x^2 – 3x = 0

Answers
Answer:
a = 1, b = - 3, c = 0
Step-by-step explanation:
The standard form of a quadratic equation is
ax² + bx + c = 0 ( a ≠ 0 )
compare x² - 3x = 0
with a = 1, b = - 3, c = 0
Pythagorean Theorem Determine the length of the missing side?

Answers
7^2+10^2=c^2
49+100=c^2
149=c^2
12.2=c
Answer:
c= sqrt149; 12.2 rounded
Step-by-step explanation:
Pythagorean Theorem to find c(hypotenuse): a^2+b^2=c^2
7^2+10^2=149
sqrt149= 12.2 rounded
Find all possible topologies of the space = {x, y, z}, identify which of these topologies satisfy the Frechet property and which the Hausdorff property.
Answers
The topologies {∅, {x}, {y}, {z}, {x, y, z}} and {∅, {x}, {y}, {z}, {x, y}, {y, z}, {x, z}} satisfy both the Frechet and Hausdorff properties.
To find all possible topologies of the space = {x, y, z}, we need to consider all the possible subsets of this set. Since the set has three elements, there are 2^3 = 8 possible subsets.
The possible topologies are as follows:
1. {∅, {x, y, z}}: This is the trivial topology, where the whole set and the empty set are the only open sets.
2. {∅, {x}, {y}, {z}, {x, y, z}}: This is the discrete topology, where every subset of the set is open.
3. {∅, {x}, {y}, {z}, {x, y}, {y, z}, {x, z}, {x, y, z}}: This is the indiscrete or trivial topology, where only the whole set and the empty set are open.
4. {∅, {x}, {y}, {z}, {x, y}, {y, z}, {x, z}}: This is a topology that is not discrete or indiscrete.
To determine which of these topologies satisfy the Frechet property and the Hausdorff property, we need to consider the limit points and the ability to separate points, respectively.
The Frechet property states that for every point x in a set A, there exists a sequence of points in A that converges to x. In other words, every point is a limit point.
The Hausdorff property states that for any two distinct points x and y in a set A, there exist disjoint open sets U and V such that x is in U and y is in V. In other words, every pair of distinct points can be separated by open sets.
Let's analyze each topology:
1. {∅, {x, y, z}}: This topology does not satisfy the Frechet or Hausdorff property because it does not have any limit points or allow for the separation of points.
2. {∅, {x}, {y}, {z}, {x, y, z}}: This topology satisfies both the Frechet and Hausdorff properties. Any point x can be approached by the sequence (x), and any two distinct points can be separated by open sets.
3. {∅, {x}, {y}, {z}, {x, y}, {y, z}, {x, z}, {x, y, z}}: This topology does not satisfy the Frechet or Hausdorff property because it does not have any limit points or allow for the separation of points.
4. {∅, {x}, {y}, {z}, {x, y}, {y, z}, {x, z}}: This topology satisfies both the Frechet and Hausdorff properties. Any point x can be approached by the sequence (x), and any two distinct points can be separated by open sets.
Learn more about topologies
https://brainly.com/question/31913704
#SPJ11
what is the sum of 2/3 and 4/5
Answers
Answer:
1 7/15 or 22/15
Step-by-step explanation:
2/3 = 10/15
4/5 = 12/15
Answer:
2/15
Step-by-step explanation:
if a nonlinear system of equations contains one linear function that touches the quadratic function at its maximum, then the system has which of the following? a. no solution b. one solution c. two solutions d. infinitely many solutions
Answers
When a nonlinear system of equations contains one linear function that touches the quadratic function at its maximum, then the system has one solution
A system of equations is considered nonlinear if it contains at least one nonlinear equation. One linear function in a nonlinear system of equations touches the quadratic function at maximum. It illustrates one solution.
The given system of equation is presented as follows;
Linear function: f(x) = mx + c
Quadratic function: f(x) = ax² + bx + c
It should be noted that given that the linear function touches the quadratic function at maximum we have;
ax² + bx + c = 0
Therefore, if a nonlinear system of equations contains one linear function that touches the quadratic function at its maximum has one solution.
Learn more about nonlinear system of equations on:
https://brainly.com/question/11650202
#SPJ4
2. What is an algebraic expression for the word phrase: 4 times the difference of a and p?
a. 4 - ap
b. 4(a-p)
c. 4ap
d. 4a -p
Answers
Solve for Quadratic Equations
10x2 + 20x− 71 = 9
Answers
Answer:
x=2 or x=-4. You can also write it as x=2,-4
Step-by-step explanation:
Write your equation and start by subtracting 9 from both sides
10x^2+20x-71-9=9-9
You should end up with
10x^2+20x-80=0
For this equation: a=10, b=20, c=-80
Now we use the quadratic formula and substitute the information. I have attached a picture for you.

Let A = {1, 2, 3, 4, 5, 6}.
The distinct equivalence classes resulting from an equivalence relation R on A are
{1, 4, 5},{2, 6} and {3}. What is R?
Answers
The value of R when A = {1, 2, 3, 4, 5, 6} and the distinct equivalence classes resulting from an equivalence relation R on A are {1, 4, 5}, {2, 6} and {3} is {(1,1), (4,4), (5,5), (1,4), (4,1), (1,5), (5,1), (4,5), (5,4), (2,2), (6,6), (2,6), (6,2), (3,3)}.
Given the distinct equivalence classes resulting from an equivalence relation R on A are {1, 4, 5},{2, 6} and {3}. We need to find R.
We know that the distinct equivalence classes of an equivalence relation on A, say R, will partition A.
Therefore we need to put every element of A in one of these three classes.
Now, we have to find out under what circumstances two elements in A belong to the same class.
We can do that by looking at the known equivalence classes.
Here we can assume that any two elements that are in the same class are equivalent.
Now we can write R as below;{(1,1), (4,4), (5,5), (1,4), (4,1), (1,5), (5,1), (4,5), (5,4), (2,2), (6,6), (2,6), (6,2), (3,3)}
Therefore, the relation R is: R={(1,1), (4,4), (5,5), (1,4), (4,1), (1,5), (5,1), (4,5), (5,4), (2,2), (6,6), (2,6), (6,2), (3,3)}.
Hence, the required answer is R={(1,1), (4,4), (5,5), (1,4), (4,1), (1,5), (5,1), (4,5), (5,4), (2,2), (6,6), (2,6), (6,2), (3,3)}.
To know more about equivalence relation refer here:
https://brainly.com/question/30956755
#SPJ11
Describe the end behavior of the function f(x) = 3x* + 4x + 20 by finding lim f(x) and lim f(x). X 00 X-00 lim f(x)= (Simplify your answer.) X-00 lim f(x)=(Simplify your answer.) X-00
Answers
The dominant term in the limit is 3x².lim (3x² + 4x + 20) as x → +∞ ≈ lim (3x²) as x → +∞
the limit of 3x² as x approaches positive infinity is positive infinity:
lim (3x²) as x → +∞ = +∞
so, the limit of f(x) as x approaches positive infinity is positive infinity:
lim f(x) as x → +∞ = +∞
to find the end behavior of the function f(x) = 3x² + 4x + 20, we need to evaluate the limit of the function as x approaches positive infinity (x → +∞) and as x approaches negative infinity (x → -∞).
1. as x approaches positive infinity (x → +∞):lim f(x) as x → +∞ = lim (3x² + 4x + 20) as x → +∞
to find this limit, we focus on the term with the highest degree, which is 3x². as x becomes larger and larger (approaching positive infinity), the other terms (4x and 20) become negligible compared to 3x². as x approaches negative infinity (x → -∞):
lim f(x) as x → -∞ = lim (3x² + 4x + 20) as x → -∞
using the same reasoning as above, the dominant term in the limit is still 3x².
lim (3x² + 4x + 20) as x → -∞ ≈ lim (3x²) as x → -∞
the limit of 3x² as x approaches negative infinity is positive infinity:
lim (3x²) as x → -∞ = +∞
so, the limit of f(x) as x approaches negative infinity is positive infinity:
lim f(x) as x → -∞ = +∞
in summary:lim f(x) as x → +∞ = +∞
lim f(x) as x → -∞ = +∞
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
PLS HELP WILL MARK YOU BRAINLIEST! NO FAKE ANSWERS!


Answers
answer:
y = 114° and x = 120°
step-by-step explanation:
part A:
one inner angle: 51°second inner angle: (180°-87°) = 93°third inner angle: (180°-30°) = 150°fourth, beside y angle: 360° - 150° - 93° - 51° = 66° then y = 180° - 66° = 114°part B:
there are 6 sides, so inner angle: (6-2)*180 = 720°160° + 123° + 107° + 90° + x + x = 720°2x + 480° = 720°2x = 720° = 480°2x = 240°x = 120°#1
Let the angle beside y be x
\(\\ \rm\hookrightarrow x+51+(180-87)+(180-30)=360\)
\(\\ \rm\hookrightarrow x+51+93+150=360\)
\(\\ \rm\hookrightarrow x+294=360\)
\(\\ \rm\hookrightarrow x=66\)
y=180-66=114°#2
\(\\ \rm\hookrightarrow 2x+123+107+160+90=720\)
\(\\ \rm\hookrightarrow 2x+480=720\)
\(\\ \rm\hookrightarrow 2x=240\)
\(\\ \rm\hookrightarrow x=120\)
Fill in the missing number.
% of 1,000,000 = 1,000,000
Answers
Answer:
100% of 1,000,000 = 1,000,000
Step-by-step explanation:
hope this helps:P
Which of the following represents 8 square root x5
Answers
Answer:
\(5 \sqrt{8}\)
Example 3: A rectangular garden has a length of (x + 4) feet and a width of (x+3) feet.
What is the perimeter of the garden?
Answers
9514 1404 393
Answer:
4x +14 . . . feet
Step-by-step explanation:
The perimeter is given by ...
P = 2(L+W)
P = 2((x +4) +(x +3)) = 2(2x +7)
P = 4x +14
The perimeter of the garden is 4x +14 feet.
Please help its easy!
The table shows the location of four cities relative to sea level.
Which city is closest to sea level? Explain.
City Location Relative to Sea Level
A –0.25 meter
B 74 meters
C −32 meters
C 0.5 meter
City A; –0.25 is closest to 0 on a number line.
City B; 74 has the greatest absolute value.
City C; −32 is farthest from 0 on a number line.
City D; 0.5 has the least absolute value.
Answers
Answer:
The correct answer is City D.
Step-by-step explanation:
When you say the phrase, "closer to sea level" you mean the closest to the very top of the sea, like "0" on a number line.
This means, that whether it is to the left of the right of the number line (or above or below the sea) whichever one has the lowest absolute value is the closest.
Therefore, the correct answer is City D.
Hope this helps! :D
What are the zeros of the quadratic function f(x) = 2x² + 16x - 9?
7
O x = -4 -
-√7
and x = -4 +
+√√2/2
O x=-4- 25
and x = 4 +
-
2
21
0 x = -4-√²/²
and x = -4 +
2
41
Ox=-4-
and x = -4 +
2
|~~
25
2
21
2
41
2

Answers
The zeros of the quadratic function f(x) = 2x² + 16x - 9 are given as follows:
\(x = -4 + \sqrt{\frac{41}{2}}, x = -4 - \sqrt{\frac{41}{2}}\)
What is a quadratic function?A quadratic function is given according to the following rule:
\(y = ax^2 + bx + c\)
The solutions are:
\(x_1 = \frac{-b + \sqrt{\Delta}}{2a}\)
\(x_2 = \frac{-b - \sqrt{\Delta}}{2a}\)
In which:
\(\Delta = b^2 - 4ac\)
In this problem, the equation is given by:
f(x) = 2x² + 16x - 9.
The coefficients are a = 2, b = 16, c = -9, hence:
\(\Delta = 16^2 - 4(2)(-9) = 328\)
Then:
\(x_1 = \frac{-16 + \sqrt{328}}{2(2)} = -4 + \sqrt{\frac{41}{2}}\)
\(x_2 = \frac{-16 - \sqrt{328}}{2(2)} = -4 - \sqrt{\frac{41}{2}}\)
More can be learned about quadratic functions at https://brainly.com/question/24737967
#SPJ1
ariana was looking at rent costs for 5 55 apartments. each rent was a different amount between $ 1 , 000 $1,000dollar sign, 1, comma, 000 and $ 1 , 400 $1,400dollar sign, 1, comma, 400 per month, except for one apartment whose rent was $ 4 , 800 $4,800dollar sign, 4, comma, 800 per month. [hide data] ariana looked at the mean and median of the rents. then, she decided to remove the $ 4 , 800 $4,800dollar sign, 4, comma, 800 rent from the set and recalculate the mean and median. how will removing this rent affect the mean and median? choose 1 answer: choose 1 answer:
Answers
If Ariana removes the $4,800 rent from the set, the mean and median of the remaining rents will decrease because $4,800 is a very high value compared to the other rents.
Before removing the $4,800 rent, the mean can be calculated by adding up all the rents and dividing by the total number of rents (5):
Mean = (1,000 + 1,200 + 1,300 + 1,400 + 4,800) / 5 = 2,540
The median is the middle value in the set, which is 1,300.
After removing the $4,800 rent, the new mean can be calculated by adding up the remaining rents and dividing by the new total number of rents (4):
New Mean = (1,000 + 1,200 + 1,300 + 1,400) / 4 = 1,225
The new median is still 1,300 because it is the middle value in the remaining set.
Therefore, removing the $4,800 rent will decrease both the mean and median of the remaining rents.
To know more about mean and median:
https://brainly.com/question/28670966
#SPJ4
Suppose that we have two events, A and B, with P(A) = 0.50, P(B) = 0.60, and P(A ∩ B) = 0.45. If needed, round your answer to three decimal digits.
Find P(A | B)
Find P(B | A
Are A and B independent? Why or why not?
Answers
The probability of event A given event B, denoted as P(A | B), is 0.750. The probability of event B given event A, denoted as P(B | A), is 0.900. A and B are not independent events because the conditional probabilities P(A | B) and P(B | A) are not equal to the marginal probabilities P(A) and P(B), respectively.
To find P(A | B), we use the formula:
P(A | B) = P(A ∩ B) / P(B)
In this case, P(A ∩ B) = 0.45 and P(B) = 0.60.
Plugging these values into the formula, we get
P(A | B) = 0.45 / 0.60 = 0.750.
To find P(B | A), we use the formula:
P(B | A) = P(A ∩ B) / P(A)
Here, P(A ∩ B) = 0.45 and P(A) = 0.50.
Substituting the values, we find
P(B | A) = 0.45 / 0.50 = 0.900.
A and B are not independent because the probabilities of A and B are affected by each other. If A and B were independent, then P(A | B) would be equal to P(A), and P(B | A) would be equal to P(B). However, in this case, both P(A | B) and P(B | A) differ from their respective marginal probabilities. Therefore, A and B are dependent events.
To learn more about probability refer:
https://brainly.com/question/25839839
#SPJ11
A store manager earns $24.00 per hour. If the manager works 8 hours one day and donates 110 of the day's earnings to charity, how much of the earnings are left?
Answers
Answer:
$82.00
Step-by-step explanation:
24 times 8 = 192 - 110 = 82
Answer:
191.9
Step-by-step explanation:
24.00 * 8= 192
192- 0.1= 191.9
please help i really need this ill give brainliest if you answer it correctly
Answers
Answer:
what is the question ??
Answer:
Whats the question?
a small town in the UK has only 600 high school students. what is the largest possible sample you can take from this town and still be able to calculate the standard deviation of the sampling distribution of p-hat?
Answers
To calculate the standard deviation of the sampling distribution of p-hat, the answer will be 59 students.
By calculating,
600/10=60 and 59 students which is less than 10% of the population.
A sampling distribution, also known as a finite-sample distribution, in statistics is the probability distribution of a given random-sample-based statistic. The sampling distribution is the probability distribution of the values that the statistic takes on if an arbitrarily large number of samples, each involving multiple observations (data points), were used separately to compute one value of a statistic (such as, for example, the sample mean or sample variance) for each sample. Although only one sample is frequently observed, the theoretical sampling distribution can be determined.
Because they offer a significant simplification before drawing conclusions using statistics, sampling distributions are crucial in the field. They enable analytical decisions to be made based on the probability distribution of a statistic rather than the combined probability distribution of all the individual sample values
To learn more about standard deviation: https://brainly.com/question/475676
#SPJ4
You move left 2 units and down 1 unit. You end at (-5, -5.) Where did yo start
Answers
Answer:
(-3, -4)
Step-by-step explanation:
(-5, -5)
2 units right
(-3, -5)
1 unit up
(-3, -4)
just go backwards
Answer:
(-3, -4)
Step-by-step explanation:
The x value in (-5, -5) is -5 and y is -5. To find the original position you reverse the translations done to get to the current position. So you add 2 (because you move 2 units right to reverse) to the x value which gives us -3 and add 1 to the y value (because to reverse we move 1 unit up) which gives us the original y value of -4.
The polygons are regular polygons. Find the area of the shaded region.
(Do not round until the final answer. Then round to the nearest tenth as needed.)
PLEASE HELP IM BEGGING I NEED THE ANSWER I DONT KNOW HOW TO DO IT

Answers
The shaded area between the two hexagons is 128√3 square feet.
What is a regular polygon?A regular polygon is a two-dimensional shape with straight sides, where all sides are of equal length and all angles between the sides are of equal measure.
The center-to-vertex distance of the small hexagon is given as 4 ft. This means that the side length of the small hexagon is 4 ft/√3 or (4√3)/3 ft.
The distance between the small and larger hexagons is also given as 4 ft. This means that the radius of the circle circumscribing the larger hexagon is (4√3)/3 + 4 ft.
The formula for the area of a regular hexagon is:
Area = (3√3 / 2) × (side length)²
For the smaller hexagon, the side length is (4√3)/3 ft, so its area is:
Area of smaller hexagon = (3√3 / 2) × [(4√3)/3]²= 16√3 ft²
For the larger hexagon, the side length is the distance from the center to a vertex, which is the radius of the circle circumscribing the hexagon. So the area of the larger hexagon is:
Area of larger hexagon = (3√3 / 2) × [(4√3)/3 + 4]² = 144√3 ft²
Therefore, the area between the two hexagons is:
Area = Area of larger hexagon - Area of smaller hexagon
Area = 144√3 - 16√3
Area = 128√3 square feet
So the area between the two hexagons is 128√3 square feet.
To know more about regular polygons visit:
brainly.com/question/12208878
#SPJ1
When the plumber comes to my house to fix the leaky faucet,he charges a flat rate of $50 in addition to charging $22 per hour.if the final bill was $116,how long was the plumber at my house?
Answers
Answer:
Below.
Step-by-step explanation:
50+22x=116
Subtract 50 from both sides.
22x/22=66/22= 3
The plumber was at my house for 3 hours.
If the final bill was $116, the plumber was at your house for 3 hours.
How to solveThe plumber charges a flat rate of $50, so the remaining bill of $116 - $50 = $66 is the hourly charge.
Since the hourly charge is $22, the plumber was at the house for $66 / $22 = 3 hours.
Therefore, the plumber was at your house for 3 hours.
Here's a table that summarizes the steps:
Step Description Value
1 Flat rate charge $50
2 Hourly charge $66
3 Hourly rate $22
4 Hours worked $66 / $22 = 3 hours
Read more about time here:
https://brainly.com/question/30132266
#SPJ
I dont know how to solve for X. 0.8x = 3.4 and my answers are 2.6, 2.72, 4.2 and 4.25 please help me
Answers
Answer:
4.25
Step-by-step explanation:
We need to get x alone so we divide both sides by 0.8
0.8x/0.8 = 3.4/0.8Then we would get: x = 4.25
help. rhombus JKLM is shown below. Find m<KLM

Answers
Answer: It's 76 (sorry, I answered it wrong!)
Step-by-step explanation:
In a rhombus, the diagonals split the angles into two equal parts. If one part of the angle is 38, then the other part is 38. Add up both of them, and you'll get the entirety of angle L, which is 76.