what is equivalent to -1/2(1/4x-3/8)
Answers
-2x+3/16 is the answer
Related Questions
The average class size this semester in the business school of a particular university is 16 students with a standard deviation of 3.9 students. The z-score for a class with 21 students is ________.
Answers
Answer:
1.28
Step-by-step explanation:
We are given;
Population mean; μ = 16
Population standard deviation; σ = 3.9
Sample mean; x' = 21
Formula for z-score is;
z = (x' - μ)/σ
z = (21 - 16)/3.9
z = 1.28
sans and papyrus are making spaghetti
sans used 90% of the cheddar
and papyrus used the other 10%
how much are they using to make the spaghetti
Answers
Answer:
100%
Step-by-step explanation:
90+10=100
Answer:
Step-by-step explanation:
Oh god that’s 100% of the cheddar bag used! PAPYRUS NO THATS TOO MUCH YOULL RUIN UR SPAGHETTI AND SANS UR NOT HELPING. Oh god what if Sans sabotaged his spaghetti... It’s either that, or a more logical explanation: Sans used 90% of the cheddar to flavor his ketchup, while Papyrus was left with the last bit for his spaghetti...?
Papyrus: I am now going to make one of my famous spaghetti dishes with not 10%, but 20% cheddar! Sans! Give me the cheese bag!
Sans: Sure, bud. *hands over 10% of cheddar left in bag*
Papyrus: This... this is only 10% though... now I can’t make my soon to be famous 20% cheese spaghetti... OH MY GOD THIS IS A DISASTER
One like = giving Papyrus that last 10% he needs for his famous spaghetti

How many yards in 70 meters
Answers
Answer:
76.553 yards
Step-by-step explanation:
1m=1.094 yards
70×1.094=76.553yards
The temperature in a hotel is 21 °C.
The temperature in the hotel is 26,7°C warmer than at the top of the mountain.
The temperature at the top of the mountain is 3.2°C colder than at the bottom of the mountain.
Work out the temperature at the bottom of the mountain.
Answers
The temperature at the bottom of the mountain is 50.9 °C.
Let's work through the given information step by step to find the temperature at the bottom of the mountain.
The temperature in the hotel is 21 °C.
The temperature in the hotel is 26.7 °C warmer than at the top of the mountain.
Let's denote the temperature at the top of the mountain as T_top.
So, the temperature in the hotel can be expressed as T_top + 26.7 °C.
The temperature at the top of the mountain is 3.2 °C colder than at the bottom of the mountain.
Let's denote the temperature at the bottom of the mountain as T_bottom.
So, the temperature at the top of the mountain can be expressed as T_bottom - 3.2 °C.
Now, let's combine the information we have:
T_top + 26.7 °C = T_bottom - 3.2 °C
To find the temperature at the bottom of the mountain (T_bottom), we need to isolate it on one side of the equation. Let's do the calculations:
T_bottom = T_top + 26.7 °C + 3.2 °C
T_bottom = T_top + 29.9 °C
Since we know that the temperature in the hotel is 21 °C, we can substitute T_top with 21 °C:
T_bottom = 21 °C + 29.9 °C
T_bottom = 50.9 °C
Therefore, the temperature at the bottom of the mountain is 50.9 °C.
for such more question on temperature
https://brainly.com/question/14820864
#SPJ8
1 Use the sequence below to complete each task. 5, 10, 20, .. a. Identify the common ratio (r). b. Write an equation to represent the sequence. C. Find the 9th term (ay) Gina Wilon (All Things Algebra), 2013 Enter your answer's) here
Answers
a)
This is a geometrical sequence, which means that the common ratio is multiplied to get the next number in the sequence.
To calculate the common ratio of the sequence you have to divide one number of the set by the number below it:
\(r=\frac{10}{5}=2\)r=2
b)
"a" represents the first number of the set.
"ar" is the second number of the set
"arr" or "ar²" is the third value of the set
"ar³" is the fourth value of the set
You can repeat this as many times as you want, this is symbolized as "n-1" where n represents the number of times you repeat the multiplication and the "-1" is because the first value of the term is the only one you know and was determined before staring the sequence.
So you can calculate any value of the sequence as:
\(ar^{(n-1)}\)n is always equal or greater than 1.
To make it simpler you can replace n-1 with k, where k will represent the position in the sequence you wish to calculate:
\(\text{ar}^k\)For k is equal or greater to zero.
c)
To find the 9th term of the sequence you have to use the formula above:
a=5
r=2
k=9
\(\text{ar}^k=5\cdot2^9=2560\)3. A website is offering a promotion, during which customers can buy up to 100 photos for a flat fee. The
cost per photo varies inversely with the number of photos a customer buys, as shown in the table below.
What function models the data?
Answers
To determine the function that models the data, we need to analyze the relationship between the cost per photo and the number of photos a customer buys. From the given information, we can observe that the cost per photo varies inversely with the number of photos. This implies that as the number of photos increases, the cost per photo decreases, and vice versa.
To model this relationship, we can use the inverse variation equation, which can be expressed as:
y = k/x
Here, y represents the cost per photo, x represents the number of photos, and k is the constant of variation.
Let's examine the data given in the table to find the value of k:
Number of Photos (x) Cost per Photo (y)
10 10
25 4
50 2
100 1
We can see that as the number of photos increases, the cost per photo decreases. We can use any pair of values from the table to solve for k. Let's choose the pair (50, 2):
2 = k/50
Solving for k:
k = 2 * 50 = 100
Now that we have the value of k, we can write the function that models the data:
y = 100/x
Therefore, the function that models the data is y = 100/x, where y represents the cost per photo and x represents the number of photos a customer buys.
100 POINTS PLEASE HELP FAST
Select the correct answer.
The weight of a radioactive isotope was 96 grams at the start of an experiment. After one hour, the weight of the isotope was half of its initial weight. After two hours, the weight of the isotope was half of its weight the previous hour. If this pattern continues, which of the following graphs represents the weight of the radioactive isotope over time?

Answers
The top left graph represents the weight of the radioactive isotope over time.
How to define an exponential function?An exponential function has the definition presented according to the equation as follows:
\(y = ab^x\)
In which the parameters are given as follows:
a is the value of y when x = 0.b is the rate of change.The parameter values for the function in this problem are given as follows:
a = 96, b = 0.5.
Hence the function is given as follows:
\(y = 96(0.5)^x\)
Two points on the graph of the function are given as follows:
(1,48) and (2, 24).
Hence the top left graph represents the weight of the radioactive isotope over time.
More can be learned about exponential functions at brainly.com/question/2456547
#SPJ1
Answer:
Graph W
Step-by-step explanation:
The given information describes a radioactive decay process, where the weight of the isotope decreases by half at regular intervals. This type of decay is characteristic of exponential decay.
Based on the description, the graph that represents the weight of the radioactive isotope over time would be a decreasing exponential curve, where the y-axis represents the weight of the isotope (in grams), and the x-axis represents time (in hours).
The initial weight of the isotope is 96 grams, and after each subsequent hour, the weight becomes half of what it was in the previous hour. Therefore, the correct graph would start at 96 grams (the initial weight when x = 0) and then decrease by half every hour. It would be a curve that gets closer and closer to zero but never quite reaches it.
Initial weight: 96 grams
After 1 hour: 96 / 2 = 48 grams
After 2 hours: 48 / 2 = 24 grams
After 3 hours: 24 / 2 = 12 grams
After 4 hours: 12 / 2 = 6 grams
After 5 hours: 6 / 2 = 3 grams
So, the points on the graph would be:
(0, 96), (1, 48), (2, 24), (3, 12), (4, 6), (5, 3)Therefore, the graph that represents the weight of the radioactive isotope over time is Graph W.

Albinism in humans is autosomal and fully recessive to normal color. A couple, who are both normal, have a daughter who is albino and a son who is normal. The couple wants to have 3 more children. What is the probability that they will have 3 normal girls?
Answers
The probability that the couple will have 3 normal girls is approximately 0.422
Since both parents are normal, they both have to be heterozygous carriers for the recessive allele that causes albinism. We can represent the normal allele with the letter N and the albino allele with the letter n. Then, we can write the genotypes of the parents as Nn x Nn.
The daughter is albino, so her genotype must be nn. The son is normal, so his genotype must be Nn.
We want to find the probability that the couple will have 3 normal girls. We can use the multiplication rule of probability to find this probability:
P(3 normal girls) = P(normal girl) x P(normal girl) x P(normal girl)
The probability of having a normal girl is 3/4 since there are three possible genotypes that result in a normal phenotype (NN, Nn, Nn) out of a total of four possible genotypes. The probability of having a normal boy is also 3/4, for the same reason.
Therefore, the probability of having 3 normal children (in this case, girls) is:
P(3 normal girls) = (3/4) x (3/4) x (3/4) = 27/64 ≈ 0.422
So, the probability that the couple will have 3 normal girls is approximately 0.422, or about 42.2%.
To learn more about probability, refer:-
https://brainly.com/question/9793303
#SPJ4
Find the value of the variable. Pic has the full question. please help.

Answers
Answer:
x = 18
Step-by-step explanation:
4x and 90 - x are vertically opposite angles and are congruent, then
4x = 90 - x ( add x to both sides )
5x = 90 ( divide both sides by 5 )
x = 18
5/8 of the pie that was left.
There is of an apple pie left from dinner. Tomorrow, Victor plans to eat
7/8
Enter how much of the whole pie he will eat tomorrow.
of the pie that was left.
Answers
Answer:
he will eat 35/64 of the whole pie
Step-by-step explanation:
i hope i helped
2 QUESTIONS!
When a number is decreased by 10% of itself, the result is 27. What is the number?
Write an equation to model the problem. Use a to represent the number.
Answer:
Solve the equation to find the number:
Answer:

Answers
Answer:
30
Step-by-step explanation:
The equation will be:
x - (10% of x) = 27
x - 0.1x = 30
0.9x = 30
Divide by 0.9
x = 30
The number is 30
Second question:
Length = 2x - 3
Width = x
Perimeter = 72
Perimeter = 2(l + w)
= 2(2x - 3 + x) = 72
4x - 6 + 2x = 72
6x = 72 + 6
6x = 78
w = 78/6 = 13
The width is 13 meters
What is the slope of the line that passes through the points (5.-1) and (-3.3)? A -2 B. - C. D. 2
Answers
The slope of a straight line is calculated by the formula
\(\begin{gathered} \text{slope}=\frac{y_2-y_1}{x_2-x_1} \\ \text{The two points are:} \\ (x_1,y_1)=(5,\text{ -1)} \\ (x_2,y_2)=(-3,\text{ 3)} \end{gathered}\)Hence,
\(\begin{gathered} \text{slope}=\frac{3-(-1)}{-3-5} \\ =\frac{3+1}{-8} \\ =\frac{4}{-8} \\ =-\frac{1}{2} \end{gathered}\)Option B is the correct
Solve the equation.
−(x + 2) − 2x = −2(x + 1)
x= [?]
Answers
Step-by-step explanation:
-x-2-2x=-2x-2
-x-2=-2
x=0
the answer is x= 0
![Solve the equation.(x + 2) 2x = 2(x + 1)x= [?]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/5utoVutmCQ1miQK2eQAFIHatEfHlK4mf.png)
\(\sqrt{x} -3\sqrt[4]{x} -4=0\\\)
Answers
Answer:
Step-by-step explanation: \((\sqrt[4]{x})^{2} - 3\sqrt[4]{x} -4=0\)
\(\sqrt[4]{x} = u\) ⇒ u² - 3u -4 =0 ⇒ \(\left \{ {{u=4} \atop {u=-1}} \right.\) choose u=4 ( \(\sqrt{x} > 0\) )
⇒ x=256
2) Ayanda wants to invest R200 000. The bank offers him 2 options for his
6 year investment.
Option 1: 12% Simple interest p.a.
Option 2: 9,5% Compound interest p.a.
4.2.1) Calculate the return on Ayanda's investment using Option 1.
●
●
4.2.2) Calculate the return on Ayanda's investment using Option 2.
4.2.3) Which option will render the most money?
Answers
Answer:
4.2.1) R140 000
4.2.2) R144 758.28
4.2.3) Option 2
Step-by-step explanation:
To calculate the return on Ayanda's investment using Option 1, we can use the simple interest formula.
\(\boxed{\begin{minipage}{7 cm}\underline{Simple Interest Formula}\\\\$ I =Prt$\\\\where:\\\\ \phantom{ww}$\bullet$ $I =$ interest accrued \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}\)
Given values:
P = R200 000r = 12% = 0.12t = 6 yearsSubstitute the given values into the formula and solve for I:
\(I=200000 \cdot 0.12 \cdot 6\)
\(I=24000 \cdot 6\)
\(I=144000\)
Therefore, the return on Ayanda's investment using Option 1 is R144000.
\(\hrulefill\)
To calculate the return on Ayanda's investment using Option 2, we can use the compound interest formula.
\(\boxed{\begin{minipage}{7 cm}\underline{Annual Compound Interest Formula}\\\\$ I=P\left(1+r\right)^{t}-P$\\\\where:\\\\ \phantom{ww}$\bullet$ $I =$ interest accrued \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}\)
Given values:
P = R200 000r = 9.5% = 0.095t = 6 yearsSubstitute the given values into the formula and solve for I:
\(I=200000(1+0.095)^6-200000\)
\(I=200000(1.095)^6-200000\)
\(I=200000(1.72379142...)-200000\)
\(I=344758.28426...-200000\)
\(I=144758.28426...\)
\(I=144758.28\)
Therefore, the return on Ayanda's investment using Option 2 is R144758.28.
\(\hrulefill\)
Comparing the returns from both options, we find that Option 1 offers a return of R144000, while Option 2 offers a return of R144758.28. As R144758.28 > R144000, then Option 2 will render the most money for Ayanda's investment.
Joseph has $620 to spend at a bicycle store for some new gear and biking outfits.
Assume all prices listed include tax.
• He buys a new bicycle for $440.12.
• He buys 2 bicycle reflectors for $12.86 each and a pair of bike gloves for $19.26.
• He plans to spend some or all of the money he has left to buy new biking outfits
for $53.96 each.
Answers
Answer:
https://brainly.com/question/24093265
Step-by-step explanation will be provided in the link above!
PLS HELP FIRST TO ANSWER GETS BRAINLEST

Answers
find the range of the function y = 1/2x + 2 if the domain is {-4, -2, 0}
Answers
The range of the function y = 1/2 x + 2 is {0, 1, 2}, if the domain of the function is {-4, -2, 0}.
What is function?An expression, rule, or law in mathematics that specifies the relationship between an independent variable and a dependent variable.
The given function is,
y = 1/2 x + 2.
Also, the domain of the function is {-4, -2, 0}.
Since, the domain of the functions defines the values of x,
And range defines the value of y in function.
The value of y at x = -4
y = 1/2(-4) + 2 = -2 + 2 = 0
At x = -2,
y = 1/2(-2) + 2 = -1 + 2 = 1
At x= 0,
y = 1/2 (0) + 2 = 2
The values of y are 0, 1 and 2.
Hence, the range of the function is {0, 1, 2}.
To know more about Function on:
https://brainly.com/question/2411204
#SPJ1
we have a deck of 5 cards numbered from 1 to 5.
Some are grey and some are white.
The cards numbered 2, 3, and 4 are grey.
The cards numbered 1 and 5 are white.
A card is drawn at random.
Let x be the event that the drawn card is grey, and let P(X) be the probability of X
Let not X be the event that the drawn card is not grey, and let P (not X) be the probability of not X
(a) For each event in the table, check the outcome('s) that are contained in the event. Then, in the last column, enter the probability of the
Event
X
Not X
Outcomes
12345
Probability
P(X) -
P(not X) -
1 2 3 4 5
(B) Subtract
1-P(notX)=
Select the answer that makes the sentence true
1-p(notX) is the same as
P(x)
P(notX)
1-P(x)
None of the above
Answers
The answer that makes the sentence true is: 1 - P(not X) is the same as P(X).Therefore, the correct answer is: P(X)
(a) To determine the probabilities of events X (drawing a grey card) and not X (drawing a non-grey card), we need to analyze the given information.
We are given that the cards numbered 2, 3, and 4 are grey, while the cards numbered 1 and 5 are white.
For event X (drawing a grey card), the outcomes contained in this event are 2, 3, and 4. Therefore, the probability of event X, denoted as P(X), is the number of outcomes in X divided by the total number of possible outcomes.
Since there are 5 cards in total, the probability of drawing a grey card is:
P(X) = Number of grey cards / Total number of cards
= 3 / 5
= 0.6
For event not X (drawing a non-grey card), the outcomes contained in this event are 1 and 5. Thus, the probability of event not X, denoted as P(not X), is:
P(not X) = Number of non-grey cards / Total number of cards
= 2 / 5
= 0.4
The completed table is as follows:
Event | X | Not X
Outcomes| 2, 3, 4 | 1, 5
Probability | P(X) = 0.6 | P(not X) = 0.4
(b) Subtracting 1 - P(not X) is equivalent to finding the probability of event X. Therefore, the answer that makes the sentence true is:
1 - P(not X) is the same as P(X).
Therefore, the correct answer is: P(X)
for more such question on sentence visit
https://brainly.com/question/31653526
#SPJ8
Answer ASAP but only if you are SURE about it
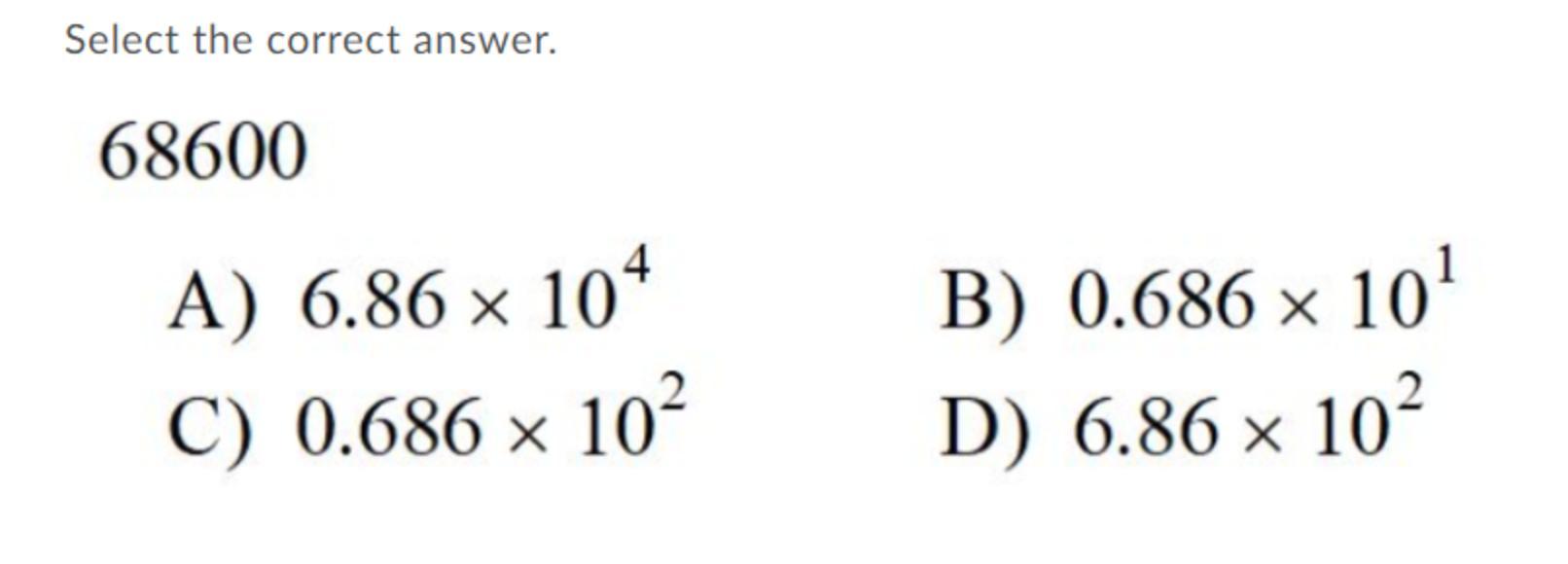
Answers
Answer:
It's A, 6.86 × 10⁴
Step-by-step explanation:
In scientific notation, you have the base, and the 10. The 10 is represented next to an exponent, whereas the base is a whole number and a decimal. If the decimal is moved right, the exponent following the 10 becomes negative. Left, it becomes positive. In this instance, the decimal is being moved left, thus the exponent is positive.
Answer:
A
Step-by-step explanation:
All my work is provided in the attached Screenshot! :)

Solve for
x
6
(
x
−
6
)
=
5
(
x
+
1
)
Answers
Answer:
x = 41
Step-by-step explanation:
6(x−6)=5(x+1)
Step 1 - Expand the brackets:
6(x - 6) = 5(x + 1)
6x - 36 = 5x + 5
Step 2 - Add 36 to both sides of the equation:
6x - 36 + 36 = 5x + 5 + 36
6x = 5x + 41
Step 3 - Subtract 5x from both sides of the equation:
6x - 5x = 5x + 41 - 5x
x = 41
Hope this helps!
\(\large\underline{\sf{Solution-}}\)
Given expression:
6(X - 6) = 5(X + 1)
⇛6X - 36 = 5X + 5
⇛6X - 5X = 5 + 36
⇛X = 41 Ans.
Read more:
Similar question
simplify 6/x-6+3x/x+5-1/(x-6)(x+5)....
https://brainly.com/question/9027174?referrer
Question 1 of 10
The mean of a distribution is 217, while the median is 217. Which of these
statements is likely to be true about the distribution?
A. It is not skewed.
B. It is negatively skewed.
C. It is positively skewed.
OD. It is not symmetrical.
SUBMIT
Answers
The mean of a distribution is 217, while the median is 217.The statements is likely to be true about the distribution is option D. It is not symmetrical.
The distribution is likely to be asymmetrical if the mean and median have different values. If the mean and median of a distribution are equal, it is likely that the distribution is symmetrical, which means it has equal tail sizes on both sides. However, if the mean and median are not equal, it indicates that the distribution is skewed.
A negatively skewed distribution means that the mean is less than the median, whereas a positively skewed distribution means that the mean is greater than the median.In this case, since the mean and median of the distribution are equal, it is likely to be symmetrical. Since none of the options say "symmetrical," option D, "It is not symmetrical," is the correct answer.
Know more about symmetrical here:
https://brainly.com/question/31331083
#SPJ8
Use function notation to write the equation of the line.
please help

Answers
Answer:
f(x) = -3/2 x - 2
Step-by-step explanation:
The line rises to the left so the slope is negative, also:
the slope of the line is -3/2 and the y-intercept is at (0, -2)
4x(x + 1) − (3x − 8)(x + 4)
Answers
The simplified form of the expression 4x(x + 1) − (3x − 8)(x + 4) is -3x^2 - 4x - 32.
To simplify the expression 4x(x + 1) − (3x − 8)(x + 4), we can expand the parentheses and combine like terms.
Expanding the first term, we get 4x^2 + 4x.
Expanding the second term, we have -(3x)(x) - (3x)(4) - (-8)(x) - (-8)(4), which simplifies to -3x^2 - 12x - (-8x) - (-32), further simplifying to -3x^2 - 12x + 8x - 32.
Combining like terms, we obtain -3x^2 - 4x - 32.
For more such questions on expression
https://brainly.com/question/723406
#SPJ8
the perimeter of a rectangle is 15x+17y. if the length is 7/2x+7y, then find the width of the rectangle
A.) 4x+3/2y
B.) 8x+3y
C.) 8x+10y
D.) 4x+3y
Answers
Answer:
A
Step-by-step explanation:
Length : \(\frac{7x}{2} + 7y\)
Perimeter: \(15x + 17y\)
Perimeter = 2(Length + Width)
15x + 17y = 2( \(\frac{7x}{2} + 7y\) + Width)
15x + 17y = 7x + 14y + 2(Width)
15x + 17y -7x -14y = 2(Width)
8x + 3y = 2(Width)
Width = \(\frac{8x + 3y}{2}\)
Width = 4x + 3y/2
A bank account balance is -$26 .If a second bank account balance is less than -$26,identify a possible balance. Write an inequality to compare the balances.
Answers
The inequality to compare the balances in the accounts x <-26
How to write an inequality to compare the balances in the accounts?Based on the given parameters in the question, the balances are given as
Bank Account Balance 1 = -$26
Bank Account Balance 2 is less than Bank Account Balance 1
This above balances can be represented as be expressed as
Bank Account Balance 2 is less than Bank Account Balance 1
So, we have
x is less than Bank Account Balance 1
In this case, the variable x represents balance 2
Express less than inequality using less than inequality symbol <
So, we have the following inequality expression
x < balance 2
Substitute -26 for balance 2
x < -26
Hence, the inequality to compare the balances in the accounts x <-26
Read more about inequality at
https://brainly.com/question/24372553
#SPJ1
What are factors in the expression 4x(3x^2+5y)
Answers
Answer:
12x^3 +20xy
Step-by-step explanation:
Hope this Helped!!!!!!!!!!!!
Answer:
Technically it is 12x^3 + 20xy but the answer choice is 12 and 20.
Step-by-step explanation:
For the work, you need to distribute 4x to each term in the ( ).
i need help can someone help me right now!!!!!!

Answers
(a) | BD | bisects | AC | (reason : Given)
(b) |AD| ≅ |CD| (reason: |BD| is the perpendicular bisector of segment AC).
(c) ∠ABD ≅ ∠CBD (reason: | BD | bisects angle ABC)
(d) ∠A ≅ ∠ C (reason: complementary angles of a right triangle)
What is the complete proof of the congruent angles?Congruent angles are the angles that have equal measure. So all the angles that have equal measure will be called congruent angles.
From the first statement, we will complete the flow chart as follows;
line BD bisects line AC (reason : Given)
line AD is congruent to line CD (reason: line BD is the perpendicular bisector of segment AC)
Angle ABD is congruent to angle CBD (reason: line BD bisects angle ABC)
Angle A is congruent to angle C (reason: angle ABD = angle CBD, and both triangles ABD and CBD are right triangles).
Learn more about congruent angles here: https://brainly.com/question/28262429
#SPJ1
Customer: "A previous representative told me that I would receive a 17% discount on my $123.76 service plan. How much is the discount?" Representative: "You will receive a discount of __________
Answers
Savings: $22.30
You will receive a discount of $22.30
Answer:
$21.04
Step-by-step explanation:
123.76 x 17% = 21.0392 = 21.04
At the first stop, 17 people
got off the bus. Now there
are 35 people on the bus.
How
mony were on the
bus to begin win?
Answers
Answer:
There were 52 people on the bus to begin with.
Step-by-step explanation:
If 17 people got off and 35 were remaining then you have to add 17 + 35 = 52
Answer:
17+35=52
Step-by-step explanation:
AT BEGNING THERE WERE 52 people on bus so when the 17 people got off the bus on first stop only 35 remained.