What did I do wrong in this?? I have no idea its due soon. Sorry about my handwriting

Answers
Answer:
\(x = 16\)
Step-by-step explanation:
\( \frac{1}{2} (x + 8) - 16 = - 4\)
\( \frac{1}{2} x + 4 - 16 = - 4\)
\( \frac{1}{2} x + 4 = 12\)
\( \frac{1}{2} x = 8\)
\(x = 16\)
Answer:
Step-by-step explanation:
\(\frac{1}{2}(x + 8 ) - 16 = - 4\\\\\frac{1}{2}*x + 8*\frac{1}{2} - 16 = -4\\\\\frac{1}{2}x + 4 - 16 = -4\\\\\frac{1}{2}x -12 = -4\)
Add 12 to both sides
\(\frac{1}{2}x = -4 + 12\\\\\frac{1}{2}x = 8\\\)
Multiply both sides by 2
\(x = 8*2\\\\x = 16\)
Related Questions
Assume that the circle is a unit circle. The sine of angle a is 0.7. Who’s is cos(a)?

Answers
Solution
\(sin\text{ }a=0.7\)\(\begin{gathered} sin\text{ a=0.7} \\ a=sin^{-1}0.7 \\ a=44.427^0 \end{gathered}\)on the second quadrant
\(180-44.427=135.572\)Now cos a
\(cos\text{ 135.572=-0.71414}\)Real I need help ppplllsss

Answers
Answer:
the answer is a or c help it help it helps
Find the solutions to the following equation. Answers as ordered pairsx^2 + 6x + 5 = 0
Answers
x² + 6x + 5 = 0
To find the solution, we can use the quadratic formula.
\(\begin{gathered} x_{1,2}=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_{1,2}=\frac{-6\pm\sqrt[]{6^2-4(1)(5)}}{2(1)} \\ x_{1,2}=\frac{-6\pm\sqrt[]{36^{}-20}}{2} \\ x_{1,2}=\frac{-6\pm4}{2} \\ x_1=\frac{-6+4}{2}=-1 \\ x_2=\frac{-6-4}{2}=-5 \end{gathered}\)The solutions are (-1, 0) and (-5, 0)
Find the exact length of the curve. x = y^4/8 + 1/4y^2 , 1 ≤ y ≤ 2
_____
Answers
The exact length of the curve is 33/16
What is an equation?
An equation is a mathematical statement that proves two mathematical expressions are equal in algebra, and this is how it is most commonly used. In the equation 3x + 5 = 14, for instance, the two expressions 3x + 5 and 14 are separated.
Given:
\(x = \frac{y^4}{8} +\frac{ 1}{4y^2}\)---------------------(1)
Arc length formula:
\(L=\int_{c}^d\sqrt{1+(\frac{dx}{dy})^2} ~~~dy\)--------------(2)
Intervals c=1. d=2
differentiate (1) with respect to y
\(\frac{dx}{dy}=\frac{4y^3}{8}+\frac{-2}{4y^3}=\frac{y^3}{2}-\frac{1}{2y^3}\)
Now,
(2)=> \(L=\int_{1}^2\sqrt{1+(\frac{y^3}{2}-\frac{1}{2y^3})^2} ~~~dy\)
Using the identity (a-b)² = a²-2ab+b² and simplifying, we get
\(L=\int_{1}^2(\frac{y^3}{2}+\frac{1}{2y^3})^2 ~~~dy\)
Integrate with respect to y
\(L= [(\frac{y^4}{8}-\frac{1}{4y^2})^2]_{1}^2\)
Apply the limits and simplifying, we get
L= 33/16
The exact length of the curve is 33/16
To learn more about the equation from the given link
https://brainly.com/question/28218072
#SPJ1
The exact length of the curve is 33/16
What is an equation?An equation is a mathematical statement that proves two mathematical expressions are equal in algebra, and this is how it is most commonly used. In the equation 3x + 5 = 14, for instance, the two expressions 3x + 5 and 14 are separated.
To find the length of the curve, we need to use the arc length formula:
L = ∫ [1, 2] √[1 + (dx/dy)²] dy
First, we need to find dx/dy:
dx/dy = 1/2 y³ + 1/2 y
Now we can substitute this into the arc length formula and simplify:
L = ∫ [1, 2] √[1 + (1/2 y^3 + 1/2 y)²] dy
L = ∫ [1, 2] √[1 + 1/4 y⁶ + y⁴ + 1/4 y²] dy
L = ∫ [1, 2] √[1/4 y⁶ + y⁴ + 1/4 y² + 1] dy
We can now use a trigonometric substitution, letting y² = tanθ:
y² = tanθ
2y dy = dθ
When y = 1, θ = π/4 and when y = 2, θ = π/3. So we can rewrite the integral as:
L = 2∫ [π/4, π/3] √[1/4 tan⁴θ + tan²θ + 1] dθ
We can then use a second substitution, letting u = tanθ:
u = tanθ
du/dθ = sec²θ
dθ = du/u²
Substituting this into the integral, we get:
L = 2∫ [1, √3] √[1/4 u⁴ + u² + 1] du/u²
We can simplify the integrand by multiplying both the numerator and the denominator by u²:
L = 2∫ [1, √3] √[u⁴/4 + u⁴ + u²] du/u⁴
L = 2∫ [1, √3] √[5/4 u⁴ + u²] du/u⁴
Now we can use a substitution, letting v = u²:
v = u²
du = dv/2√v
Substituting this into the integral, we get:
L = 4∫ [1, 3] √[5/4 v² + v] dv/v³
L = 4∫ [1, 3] √[5v² + 4v] dv/v³
At this point, we can use a partial fraction decomposition to evaluate the integral:
√[5v² + 4v]/v³ = A/v + B/v² + C/√[5v² + 4v]
Multiplying both sides by v³ and simplifying, we get:
√[5v² + 4v] = Av²√[5v² + 4v] + Bv + Cv³√[5v² + 4v]
We can solve for A, B, and C by equating coefficients:
A = 0
B = 1/2
C = √(5)/2
Now we can substitute these values back into the partial fraction decomposition:
√[5v² + 4v]/v³ = 1/2v + 1/2v² + √(5)/2 sqrt[5v² + 4v]
Substituting this back into the integral and evaluating, we get:
L = 4[1/2lnv + 1/2v - 1/√(5)ln(√(5)v + 2
To learn more about the equation from the given link
brainly.com/question/28218072
#SPJ1
5. Which equation is solved for the height of the cone based on theinformation given below?The equation V = 1 r represents the volume of a cone, where is the radius of the cone andh is the height of the coneh=V - Tr?h= } #r?VB3V - #r2 = h3Vha?D

Answers
We need to make h the subject of formula:
\(\begin{gathered} All\text{ the variables on the right are multiplied together.} \\ \text{First we get rid of the 1/3 by multiplying both sides by 3:} \\ 3(V)\text{ =3( }\frac{1}{3}\pi r^{2}h) \\ 3V\text{ = }\pi r^{2}h \end{gathered}\)\(\begin{gathered} \text{For h to stand alone on the right side, we divide both sides by }\pi r^2h \\ We\text{ apply division beause all the variables were ultiplied together} \\ So\text{ to undo it, we divide} \\ \frac{3V}{\pi r^{2}}=\text{ }\frac{\pi r^{2}h}{\pi r^{2}} \\ \frac{3V}{\pi r^2}=\text{ }h \end{gathered}\)\(h\text{ = }\frac{3V}{\pi r^{2}}\text{ (option D)}\)If the joint probability density of X and Y is given by Find a) Marginal density of X b) Conditional density of Y given that X-1/4 c) P(Y < 1/X = ¹) d) E (YX =) and Var(Y)X = ¹) e) P(Y < 1|X<=) f) Let X and Y have a bivariate Normal distribution with X-N(70,100) respectively, and p = 5/13. Evaluate P(Y S841X= 72). [ 14 marks] (2x+y) for 0
Answers
Answer : a. The marginal density of X is f(x) = 2x + 1/2b)
b.conditional density of Y given that X = 1/4 = 1/2+y for 0
Explanation :
Given, the joint probability density of X and Y is: f(x,y) = (2x+y) for 0 < x < 1, 0 < y < 1a)
Marginal density of X:
We can find the marginal probability density function of X by integrating the joint probability density function f(x,y) over all possible values of Y.f(x) = ∫f(x,y)dy
Here,f(x) = ∫0 to 1 (2x+y) dy = 2x + 1/2
Therefore, the marginal density of X is f(x) = 2x + 1/2b)
a) Marginal density of X : The marginal density of X is given by integrating the joint density function of X and Y with respect to Y over the whole range of Y.
Thus,marginal density of X = ∫f(x,y)dy from -∞ to +∞marginal density of X = ∫[2x+y] dy from -∞ to +∞
Here, the limits of integration for Y are -∞ and +∞. Integrating with respect to Y gives us,marginal density of X = [2x(y)] evaluated from -∞ to +∞marginal density of X = [2x(+∞) - 2x(-∞)]
marginal density of X = ∞ for all values of x
b) Conditional density of Y given that X-1/4
The conditional density of Y given that X = x is given by dividing the joint density function by the marginal density of X and then setting X = x. Thus,conditional density of Y given that X = x = f(x,y)/fX(x)
conditional density of Y given that X = 1/4 = f(1/4,y)/fX(1/4)
Substituting the given values in the above equation, we get,conditional density of Y given that X = 1/4 = [2(1/4)+y]/∞
conditional density of Y given that X = 1/4 = 1/2+y for 0
Learn more about joint probability here https://brainly.com/question/32099581
#SPJ11
Thomas lives more than 0. 55 km and less than 0. 75 km from his school.
Thomas lives from his school?
A. 0. 06 km
B 0. 50 km
c. 0. 60 km
D. 1. 30 km
Which choice could be the distance Thomas lives from school?
Answers
Answer:
D. answer po
Step-by-step explanation:
Tama yan na D
Solve the following maximisation problem by applying the Kuhn-Tucker theorem: Max xy subject to –4x^2 – 2xy – 4y^2 x + 2y ≤ 2 2x - y ≤ -1
Answers
By applying the Kuhn-Tucker theorem, the maximum value of xy is: 18/25
The constraints are:-4x² - 2xy - 4y²x + 2y ≤ 22x - y ≤ -1
Let us solve this problem by applying the Kuhn-Tucker theorem.
Let us first write down the Lagrangian function:
L = xy + λ₁(-4x² - 2xy - 4y²x + 2y - 2) + λ₂(2x - y + 1)
Then, we find the first order conditions for a maximum:
Lx = y - 8λ₁x - 2λ₁y + 2λ₂ = 0
Ly = x - 8λ₁y - 2λ₁x = 0
Lλ₁ = -4x² - 2xy - 4y²x + 2y - 2 = 0
Lλ₂ = 2x - y + 1 = 0
The complementary slackness conditions are:
λ₁(-4x² - 2xy - 4y²x + 2y - 2) = 0
λ₂(2x - y + 1) = 0
Now, we solve for the above equations one by one:
From equation (3), we can write 2x - y + 1 = 0, which implies:y = 2x + 1
Substitute this in equation (1), we get:
8λ₁x + 2λ₁(2x + 1) - 2λ₂ - x = 0
Simplifying, we get:
10λ₁x + 2λ₁ - 2λ₂ = 0 ... (4)
From equation (2), we can write x = 8λ₁y + 2λ₁x
Substitute this in equation (1), we get:
8λ₁(8λ₁y + 2λ₁x)y + 2λ₁y - 2λ₂ - 8λ₁y - 2λ₁x = 0
Simplifying, we get:
-64λ₁²y² + (16λ₁² - 10λ₁)y - 2λ₂ = 0 ... (5)
Solving equations (4) and (5) for λ₁ and λ₂, we get:
λ₁ = 1/20 and λ₂ = 9/100
Then, substituting these values in the first order conditions, we get:
x = 2/5 and y = 9/5
Therefore, the maximum value of xy is:
2/5 x 9/5 = 18/25
Hence, the required answer is 18/25.
Learn more about Lagrangian function at:
https://brainly.com/question/13314103
#SPJ11
A traffic engineering study on traffic delay was conducted at intersections with signals on urban streets. Three types of traffic signals were utilized in the study: (1) pretimed, (2) semi-actuated, and (3) fully actuated. Five intersections were used for each type of signal. The measure of traffic delay used in the study was the average stopped time per vehicle at each of the intersections (seconds/vehicle). The data follow Pretimed Semi-actuated Fully actuated 36.6 17.5 15.0
39.2 20.6 10.4
30.4 18.7 18.9
37.1 25.7 10.5 34.1 22.0 15.2 Source: W. Reilly, C. Gardner, and J. Kell (1976). A technique for measurement of delay at intersections. Technical Report FHWA-RD-76- 135, Federal Highway Administration, Office of R &D, Washington, D.C. Use the data from Exercise 1 to determine how many intersections the traffic engineer would need for each type of traffic signal to reject the null hypothesis at the .01 level of significance witha power of .90 if mean delays at the three traffic signal types were 20, 18, and 16 seconds, respectively.
Answers
The average number of intersections the traffic engineer would need for each type of traffic signal to reject the null hypothesis at the 0.01 level of significance with a power of 0.90 is six
To test the effectiveness of these signals, the engineer must reject the null hypothesis, which states that there is no significant difference in the mean delays between the three types of signals. The engineer wants to reject the null hypothesis at the 0.01 level of significance with a power of 0.9. In other words, they want to be 90% sure that they can detect a significant difference if it exists.
Using the data provided in the study, the engineer can calculate the sample size needed for each type of signal. They need at least five intersections for pretimed signals, six intersections for semi-actuated signals, and four intersections for fully actuated signals to reject the null hypothesis at the desired level of significance with a power of 0.9.
To know more about average here
https://brainly.com/question/16956746
#SPJ4
What type of slop..
Undefined
Positive slope
Zero slope
Negative slope

Answers
Answer:
zero slope
Step-by-step explanation:
Answer:
it's a zero slope
Step-by-step explanation:
What is the sum........
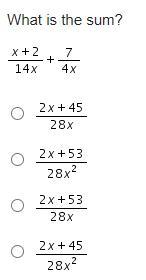
Answers
Answer:
it's the last one
Step-by-step explanation:
the last one is the correct one
help me pleaseeeeeeeeee

Answers
Answer:
Acute
Step-by-step explanation:
Answer:
If you are finding out the lower angles they are acute but the top is right
Step-by-step explanation:
Stacy starts a savings account with $15. Each month she deposits 6$ more into her
account. Stacy now has $81 in her account. Write an equation, then solve, to find how
many months Stacy has deposited money into her savings account.
Answers
Answer:
After 11 months, Stacy will have $81 in her savings account.
Step-by-step explanation:
15 + 6m = 81
6m = 66
m = 11
7xy÷Z=zz please help
Answers
Could you please write the question more clear?
The dimension of the row space of a 3 x 3 matrix A is 2. (a) What is the dimension of the column space of A? (b) What is the rank of A? (c) What is the nullity of A? (d) What is the dimension of the solution space of the homogeneous system Ax = 0?
Answers
a) the dimension of its column space is also 2. b) the rank of A is 2. c) the nullity of matrix A is 1. d) the dimension of the solution space of the homogeneous system \(A_x = 0\) is also 1.
(a) The dimension of the row space of a matrix is equal to the dimension of its column space. So, if the dimension of the row space of matrix A is 2, then the dimension of its column space is also 2.
(b) The rank of a matrix is defined as the maximum number of linearly independent rows or columns in the matrix. Since the dimension of the row space of matrix A is 2, the rank of A is also 2.
(c) The nullity of a matrix is defined as the dimension of the null space, which is the set of all solutions to the homogeneous equation Ax = 0. In this case, the matrix A is a 3 x 3 matrix, so the nullity can be calculated using the formula:
nullity = number of columns - rank
nullity = 3 - 2 = 1
Therefore, the nullity of matrix A is 1.
(d) The dimension of the solution space of the homogeneous system Ax = 0 is equal to the nullity of the matrix A. In this case, we have already determined that the nullity of matrix A is 1. Therefore, the dimension of the solution space of the homogeneous system \(A_x = 0\) is also 1.
Know more about matrix here:
brainly.com/question/24079385
#SPJ4
Expand & simplify
(x + 2)(x + 6)
Answers
Step-by-step explanation:
=(x+2)(x+6)
=x²+6x+2x+12
=x²+8x+12
hope it helps..
Answer:
x^2+8x+12
Step-by-step explanation:
expanding the answer:x*x+8*x+12
Test the claim that the mean gpa of night students is larger than 2.1 at the 0.10 significance level. the null and alternative hypothesis would be:______.
Answers
For a clinical trial (study) on the mean GPA of night students, the appropriate null and alternative hypotheses would be given by:
H₀: p = 2.1H₁: p > 2.1What is a null hypothesis?A null hypothesis (H₀) can be defined the opposite of an alternate hypothesis (H₁) and it asserts that two (2) possibilities are the same.
For a clinical trial (study) on the mean GPA of night students, the appropriate null and alternative hypotheses would be given by:
H₀: p = 2.1H₁: p > 2.1In conclusion, we can infer and logically deduce that this test would be right-tailed.
Read more on null hypothesis here: https://brainly.com/question/23822387
#SPJ4
Gator Beverages produces soda cans that are sold in cans labeled as having 12 ounces of soda. If the soda content is below 12 ounces, the customer is being unduly denied product they have paid for. Filling each can with more than 12 ounces costs the company money since it essentially means giving away free product. Accordingly, Gator Beverages have set specification of 11.8 and 12.2 ounces for the volume of soda in a can. Currently the cans are filled automatically by a filling machine and they have an average volume of soda of 11.92 ounces. What is the maximum standard deviation that the process can have that would allow Gator beverage to claim they have a six-o capability? O 0.0467 0.0200 O 0.0333 O 0.0133 0.0383 O None of the other answers are within 0.0025
Answers
The maximum standard deviation that would allow Gator Beverages to claim they have a six-sigma capability is 0.0467.
To determine the maximum standard deviation that would allow Gator Beverages to claim they have a six-sigma capability, we need to calculate the process capability index (Cpk).
The Cpk value represents how well a process meets the specified requirements.
Cpk is calculated using the formula:
Cpk = min((USL - mean) / (3 * standard deviation), (mean - LSL) / (3 * standard deviation))
Where:
USL is the upper specification limit (12.2 ounces in this case)LSL is the lower specification limit (11.8 ounces in this case)mean is the average volume of soda (11.92 ounces in this case)standard deviation is the standard deviation of the process (to be determined)Let's calculate the Cpk using the given values:
Cpk = min((12.2 - 11.92) / (3 * standard deviation), (11.92 - 11.8) / (3 * standard deviation))
To claim six-sigma capability, we want the Cpk value to be at least 2.0. Therefore, we can set up the inequality:
Cpk ≥ 2.0
Substituting the formula for Cpk:
min((12.2 - 11.92) / (3 * standard deviation), (11.92 - 11.8) / (3 * standard deviation)) ≥ 2.0
Simplifying the inequality:
(0.28 / (3 * standard deviation)) ≥ 2.0
0.28 ≥ 6 * standard deviation
standard deviation ≤ 0.28 / 6
standard deviation ≤ 0.0467
Therefore, the maximum standard deviation that would allow Gator Beverages to claim they have a six-sigma capability is 0.0467.
Learn more about Standard Deviation at
brainly.com/question/29115611
#SPJ4
How large should we choose n so that the trapezoid-rule approximation, Tn, to the integral sin r dz is accurate to within 0.00001? (Use the error bound given in Section 5.9 of the course text.)
Answers
The trapezoidal rule is a numerical integration method that uses trapezoids to estimate the area under a curve. The trapezoidal rule can be used for both definite and indefinite integrals. The trapezoidal rule approximation, Tn, to the integral sin r dz is given by:
Tn = (b-a)/2n[f(a) + 2f(a+h) + 2f(a+2h) + ... + 2f(b-h) + f(b)]where h = (b-a)/n. To determine how large n should be so that Tn is accurate to within 0.00001, we can use the error bound given in Section 5.9 of the course text. According to the error bound, the error, E, in the trapezoidal rule approximation is given by:E ≤ ((b-a)³/12n²)max|f''(x)|where f''(x) is the second derivative of f(x). For the integral sin r dz, the second derivative is f''(r) = -sin r. Since the absolute value of sin r is less than or equal to 1, we have:max|f''(r)| = 1.
Substituting this value into the error bound equation gives:E ≤ ((b-a)³/12n²)So we want to choose n so that E ≤ 0.00001. Substituting E and the given values into the inequality gives:((b-a)³/12n²) ≤ 0.00001Simplifying this expression gives:n² ≥ ((b-a)³/(0.00001)(12))n² ≥ (b-a)³/0.00012n ≥ √(b-a)³/0.00012Now we just need to substitute the values of a and b into this expression. Since we don't know the upper limit of integration, we can use the fact that sin r is bounded by -1 and 1 to get an upper bound for the integral.
For example, we could use the interval [0, pi/2], which contains one full period of sin r. Then we have:a = 0b = pi/2Plugging in these values gives:n ≥ √(pi/2)³/0.00012n ≥ 5073.31Since n must be an integer, we round up to the nearest integer to get:n = 5074Therefore, we should choose n to be 5074 so that the trapezoidal rule approximation, Tn, to the integral sin r dz is accurate to within 0.00001.
To know more about integration visit :
https://brainly.com/question/31744185
#SPJ11
The y-intercept in the linear equation y=−1/10x−2 is _[blank]_.
Enter your answer as the value that correctly fills in the blank, like this: 42
If your answer is a fraction, enter it formatted like this: 42/53
Answers
Answer:
-2 is the answer
Step-by-step explanation:
y=mx+b
b= y intercept
because it is a negative it replaces the addition sign so that it is not a positive 2.
An isosceles triangle has an angle that measures 66°. Which other angles could be in that isosceles triangle?
Answers
Answer:
57 and 57 or 66 and 48
Step-by-step explanation:
180-66=114
114/2=57
the awnser is 24
Step-by-step explanation:
I think it might be wrong sorry if it wrong
Can someone please help tell me if I got this correct?

Answers
ANSWER
1/4 n²
EXPLANATION
First, we distribute the exponent into the product,
\((2n^{-1})^{-2}=2^{-2}\cdot(n^{-1})^{-2}\)Negative exponents flip the fractions and exponents of exponents multiply,
\(2^{-2}\cdot(n^{-1})^{-2}=\frac{1}{2^2}\cdot n^{(-1)\cdot(-2)}=\frac{1}{4}n^2\)Hence, your answer is correct, 1/4n².
\(v^{3)\)-\(11v^{2}\)+13v-30)÷(v-10)
Answers
Answer:
\(v^2-v+3\)
Step-by-step explanation:
\((v^3-11v^2+13v-30)\div (v-10)\\\\\frac{v^3-11v^2+13v-30}{v-10}\\\\Factorize\:\:v^3-11v^2+13v-30\\\\=\frac{\left(v-10\right)\left(v^2-v+3\right)}{v-10}\\\\\mathrm{Cancel\:the\:common\:factor:}\:v-10\\\\=v^2-v+3\)
Calculate the slope represented by the table. Please help me and explain it

Answers
Slope = change in y / change in x
Slope = 1 - - 5 / 5 - - 1
Slope = 1 + 5 / 5 + 1
Slope = 6 / 6
Slope = 1
emptying a conical tank a water tank is shaped like an inverted cone with height 6 m and base radius of 1.5 m
Answers
Given that,The height of the tank, h = 6mThe base radius of the tank, r
= 1.5m Let V be the volume of the tank.
Using the formula for the volume of a cone, we getV = 1/3 πr²h Substituting the values, we getV = 1/3 × π × (1.5)² × 6V
= 14.137m³Let's assume that the water is being emptied from the tank at the rate of k cubic meters per minute.
We first calculated the volume of the tank using the formula for the volume of a cone. Then we used the formula for the time taken to empty a tank which is given by the formula, time taken to empty the tank = V / k.
To know more about height, visit:
https://brainly.com/question/29131380
#SPJ11
1. ADEA has vertices D(8,4), E(2, 6), and F(3, 1). What are the vertices of the image after a dilation with a scale factor of 5 using the origin as the center of dilation? TO
Answers
Answer:
The vertices of the image are D' (40, 20), E' (10, 30), F' (15, 5)
Step-by-step explanation:
If the point (x, y) dilated by a scale factor k using the origin as a center of dilation, then its image is (kx, ky)
Let us use this rule to solve our question
∵ The vertices of ΔDEF are D (8, 4), E (2, 6), and F (3, 1)
∵ ΔDEF dilated by a scale factor 5
∴ k = 5
∵ The origin as the center of dilation
→ That means, multiply the coordinates of every point by 5
∴ D' = (8 × 5, 4 × 5)
∴ D' = (40, 20)
∴ E' = (2 × 5, 6 × 5)
∴ E' = (10, 30)
∴ F' = (3 × 5, 1 × 5)
∴ D' = (15, 5)
∴ The vertices of the image are D' (40, 20), E' (10, 30), F' (15, 5)
The distribution of retirement age for NFL players is normally distributed with a mean of 33 years old and a standard deviation of about 2 years. What is the percentage of players whose age is less than 31? a 30.85% b 15.87% c 71.2% d 69.15%
Answers
The correct answer is b) 15.87%, indicating that approximately 15.87% of NFL players have a retirement age less than 31 years old.
To find the percentage of players whose age is less than 31, we can use the standard normal distribution and z-scores.
First, we need to calculate the z-score for the value 31 using the formula:
z = (x - μ) / σ
where x is the value we want to find the percentage for, μ is the mean, and σ is the standard deviation.
In this case, x = 31, μ = 33, and σ = 2. Plugging these values into the formula, we get:
z = (31 - 33) / 2 = -1
Next, we can look up the cumulative probability associated with the z-score -1 in the standard normal distribution table. The cumulative probability represents the percentage of values that are less than the given z-score.
From the standard normal distribution table, the cumulative probability for z = -1 is approximately 0.1587, which corresponds to 15.87%.
Therefore, the correct answer is b) 15.87%, indicating that approximately 15.87% of NFL players have a retirement age less than 31 years old.
Know more about Retirement here :
https://brainly.com/question/31284848
#SPJ11
Your car has 10 gallons of gas. You use 1 gallon for every 20 miles you travel.
Answers
Answer:
You would travel 200 miles before running out of gas.
Step-by-step explanation:
1:20 so 10:200 each time you multiple by 10
Write 8 as a product of primes.
Use index notation
Answers
Answer:
2³
Step-by-step explanation:
8 = 2 × 2 × 2 = 2³
critical values for quick reference during this activity
Confidence level Critical value
0.90 z*=1.645
0.95 z*=1.960
0.99 z*=2.576
A poli reported 38% supprt for 4 statewide bection wath y margin of error of 4.45 percentage points
How many voters should be for a 90% confidence interval? Round up to the nearest whole number.
Answers
The critical values for quick reference are given below:Confidence level Critical value A poli reported 38% support for 4 statewide elections with a margin of error of 4.45 percentage points.
The formula for the margin of error is given by:Margin of error = Critical value * Standard errorThe standard error is given by:Standard error = √(p * (1 - p)) / nWe know that the margin of error is 4.45 percentage points. Let's determine the critical value for a 90% confidence level.z* = 1.645We know that the point estimate is
p = 0.38, and we need to determine the minimum sample size n. Rearranging the formula, we get:
n = (z* / margin of error)² * p * (1 - p)Substituting the given values, we get:
n = (1.645 / 0.0445)² * 0.38 * 0.62n
= 348.48Rounding up to the nearest whole number, we get that at least 349 voters should be surveyed for a 90% confidence interval. Therefore, the correct option is B.
To know more about values visit:
https://brainly.com/question/30145972
#SPJ11