Use Mean value theorem to prove the following √6a+3 < a+2 for all a>1
Using methods other than the Mean Value Theorem will yield no marks. {Show all reasoning}.
Hint :Choose a>1 and apply MVT to f(x)=√6x+3 −x−2 on the interval [1,a]
Answers
for all a > 1, which completes the proof using the Mean Value Theorem.
We can prove the inequality √6a+3 < a+2 for all a > 1 using the Mean Value Theorem (MVT) as follows:
Let f(x) = √6x+3 - x - 2 on the interval [1, a], where a > 1. Then f(x) is continuous and differentiable on [1, a], and so by the MVT, there exists a value c in (1, a) such that:
f(a) - f(1) = f'(c)(a - 1)
Substituting the expression for f(x) and its derivative f'(x) = (3/2√6x+3) - 1 into the above equation, we get:
√6a+3 - a - 1 = (3/2√6c+3) - 1) (a - 1)
Rearranging this equation, we get:
√6a+3 = (3/2√6c+3) (a - 1) + a + 1
Now, since a > 1, we have 2a > 2, and so a + 1 > 3. Therefore, we can write:
√6a+3 = (3/2√6c+3) (a - 1) + a + 1 < (3/2√6c+3) (a - 1) + 2a
Simplifying this inequality, we get:
√6a+3 < (3/2√6c+3 + 2) a - (3/2√6c+3 - 3)
Now, we claim that (3/2√6c+3 + 2) < 2 for all c in (1, a). This can be shown as follows:
(3/2√6c+3 + 2) < 2 if and only if 3 < 2√6c+3 if and only if (3/2)^2 < 6c+3 if and only if c > 1, which is true since c is in (1, a).
Therefore, we have:
√6a+3 < 2a - (3/2√6c+3 - 3)
Now, since c is in (1, a), we have
√6c+3 > √6+3 > 3, and so 1/√6c+3 < 1/3. Substituting this inequality into the previous equation, we get:
√6a+3 < 2a - (1/2 - 1/√6)
Now, we claim that 2 - (1/2 - 1/√6) < a + 2 for all a > 1. This can be shown as follows:
2 - (1/2 - 1/√6) < a + 2 if and only if (5/2 + 1/√6) < a + (5/2 + 1/2) if and only if 1/√6 < a, which is true since a > 1.
Therefore, we have:
√6a+3 < a + 2
for all a > 1, which completes the proof using the Mean Value Theorem.
Visit to know more about mean value theorem:-
https://brainly.com/question/19052862
#SPJ11
Related Questions
When the sample of participants is reflective of the characteristics of the population, it is said to be?
Answers
It is claimed that the sample of participants is generalizable since it reflects the characteristics of the population.
What is Generalizability? Simply said, generalizability is a measurement of the applicability of a study's findings to a larger population or set of circumstances. It is considered that a study has strong generalizability if its findings may be applied broadly to a wide range of individuals or circumstances. Researchers use generalizability in a scholarly setting. It can be characterized as the extrapolation of findings and recommendations from a study done on a sample population to the entire population.To learn more about generalizable, refer to:
https://brainly.com/question/28237221
#SPJ4
given the function f ( x ) = x − 4 x 2 − 7 x 12 . find the value(s) of x where the function is not continuous. if there is more than one answer, then list them separated by a comma.
Answers
There is point i.e., value of x where the function f(x) = x³ - 4x² - 7x +12 is not continuous.
Consider the polynomial function f(x) = x³ - 4x² - 7x +12
As we know if a function f be a function defined on an open interval containing point a where t a ∈ R be a constant, a function f is continuous at a if lim_(x→a) f(x) = f(a).
Here, the domain of polynomial function f(x) = x³ - 4x² - 7x +12 is set of all real numbers, as the function is well defined for all real values of x.
We know that every polynomial function is continuous in their domain.
This means, the polyomial function f(x) = x³ - 4x² - 7x +12 is continuous on set of all real numbers.
Therefore, there is no value of x where the polynomial function f(x) = x³ - 4x² - 7x +12 is not continuous.
Learn more about the function here:
https://brainly.com/question/28193995
#SPJ4
can you apply the properties of rational exponents to an example?
Answers
We can simplify \((16x^4)^(-1/2) to 1/(4x^2)\) using the properties of rational exponents.
Certainly! Here's an example:
Simplify the expression: \((16x^4)^(-1/2)\)
We can apply the property of rational exponents which states that \((a^m)^n = a^(m*n)\). Using this property, we get:
\((16x^4)^(-1/2) = 16^(-1/2) * (x^4)^(-1/2)\)
Next, we can simplify \(16^(-1/2)\) using the rule that \(a^(-n) = 1/a^n\):
\(16^(-1/2) = 1/16^(1/2) = 1/4\)
Similarly, we can simplify \((x^4)^(-1/2)\) using the rule that \((a^m)^n = a^(m*n)\):
\((x^4)^(-1/2) = x^(4*(-1/2)) = x^(-2)\)
Substituting these simplifications back into the original expression, we get:
\((16x^4)^(-1/2) = 1/4 * x^(-2) = 1/(4x^2)\)
Therefore, the simplified expression is \(1/(4x^2).\)
Learn more on rational exponents here
brainly.com/question/20726608
#SPJ1
Simplify each side of the equation independently to reach a common equivalent expression, Cosy sinx 1+tan x COSX sin x-sinx tanx Part: 0/2 Part 1 of 2 Left-hand side: 1+tan Show that tanx cosx sinx Statement Rulo DO 8 1 + tan tan DO ロロ Select Rule x х 5 Validate Verify that the equation is an identity. cos'a+sina Show that sina cosa + cosa = seca - sina. + Statement Rule B DO cos's + sin sina cosa + cose ロロロロロロ CO DO 0:0 Select Rule x Х 5 Validate
Answers
The equation is an identity. We can see that both the LHS and RHS have reached a common equivalent expression
To simplify each side of the equation independently and reach a common equivalent expression, we can use trigonometric identities.
Starting with the left-hand side:
1 + tan(x)
We can use the identity:
\(1 + tan^2(x) = sec^2(x)\)
To get:
1 + tan(x) = sec^2(x) - 1
Now, for the right-hand side:
cos(y) sin(x) + 1 + tan(x) cos(x) sin(x) - sin(x) tan(x)
We can factor out sin(x) and use the identity:
sin^2(x) + cos^2(x) = 1
To get:
sin(x) [cos(y) + cos(x) tan(x)] + 1 - sin(x) tan(x)
Next, we can use the identity:
1 + tan^2(x) = sec^2(x)
To substitute for tan(x) and simplify:
sin(x) [cos(y) + cos(x)/cos(x)] + 1 - sin(x)/cos(x)
sin(x) [cos(y) + 1] + cos(x)/cos(x) - sin(x)/cos(x)
sin(x) cos(y) + sin(x) + 1/cos(x) - sin(x)/cos(x)
sin(x) cos(y) + (1 - sin^2(x))/cos(x)
cos(x) sin(y) + cos(x)/cos(x)
cos(x) [sin(y) + 1]
Therefore, we have simplified both sides of the equation to:
sec^2(x) - 1 = cos(x) [sin(y) + 1]
To verify that this is an identity, we can manipulate the right-hand side:
cos(x) [sin(y) + 1]
= cos(x) sin(y) + cos(x)
= sin(x) cos(y) + 1
Now, we can substitute for sin^2(x) using the identity:
sin^2(x) = 1 - cos^2(x)
To get:
sin(a) cos(a) + cos(a) = sec(a) - sin(a)
Which is the desired result.
To show that the given equation is an identity, we need to simplify each side independently and reach a common equivalent expression.
Given equation: 1 + tan(x) = (sin(x)cos(x) + cos(x))/(cos(x) - sin(x)tan(x))
Left-hand side (LHS): 1 + tan(x)
We know that tan(x) = sin(x)/cos(x)
So, LHS becomes 1 + sin(x)/cos(x)
Right-hand side (RHS): (sin(x)cos(x) + cos(x))/(cos(x) - sin(x)tan(x))
Factor out cos(x) from the numerator:
RHS = (cos(x)(sin(x) + 1))/(cos(x) - sin(x)tan(x))
Now, divide both the numerator and the denominator by cos(x):
RHS = (sin(x) + 1)/((1 - sin(x))(sin(x)/cos(x)))
Recall that tan(x) = sin(x)/cos(x), so we can replace sin(x)/cos(x) in the denominator with tan(x):
RHS = (sin(x) + 1)/(1 - sin(x)tan(x))
At this point, we can see that both the LHS and RHS have reached a common equivalent expression:
1 + sin(x)/cos(x) = (sin(x) + 1)/(1 - sin(x)tan(x))
To learn more about equation visit;
brainly.com/question/29538993
#SPJ11
#24, i am getting \(\left[\begin{array}{cccc}1&0&0&\frac{18}{7} \\0&1&0&\frac{8}{7} \\0&0&0&\frac{2}{7} \end{array}\right]\) , im wondering if someone can check it and show their work so i may compare.
![#24, i am getting [tex]\left[\begin{array}{cccc}1&0&0&\frac{18}{7} \\0&1&0&\frac{8}{7}](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/9V7sxIkgsQHJkv5QJBGPmfC4cvfZ88F7.jpeg)
Answers
It looks like you're talking about row-reducing an augmented matrix to solve the system of equations. Your answer is almost correct. The last row should read 0, 0, 1, 2/7.
The given system translates to
\(\left[ \begin{array}{ccc|c} 2 & -3 & 1 & 2 \\ 1 & -1 & 2 & 2 \\ 1 & 2 & -3 & 4 \end{array} \right]\)
Eliminate x from the last two rows by combining -2 (row 2) and row 1, and -2 (row 3) and row 1; that is,
(2x - 3y + z) - 2 (x - y + 2z) = 2 - 2 (2)
2x - 3y + z - 2x + 2y - 4z = 2 - 4
-y - 3z = -2
and
(2x - 3y + z) - 2 (x + 2y - 3z) = 2 - 2 (4)
2x - 3y + z - 2x - 4y + 6z = 2 - 8
-7y + 7z = -6
In augmented matrix form, this step yields
\(\left[ \begin{array}{ccc|c} 2 & -3 & 1 & 2 \\ 0 & -1 & -3 & -2 \\ 0 & -7 & 7 & -6 \end{array} \right]\)
I'll omit these details in the remaining steps.
Eliminate y from the last row by combining -7 (row 2) and row 3 :
\(\left[ \begin{array}{ccc|c} 2 & -3 & 1 & 2 \\ 0 & -1 & -3 & -2 \\ 0 & 0 & 28 & 8 \end{array} \right]\)
Multiply the last row by 1/28 :
\(\left[ \begin{array}{ccc|c} 2 & -3 & 1 & 2 \\ 0 & -1 & -3 & -2 \\ 0 & 0 & 1 & 2/7 \end{array} \right]\)
Eliminate z from the second row by combining 3 (row 3) and row 2 :
\(\left[ \begin{array}{ccc|c} 2 & -3 & 1 & 2 \\ 0 & -1 & 0 & -8/7 \\ 0 & 0 & 1 & 2/7 \end{array} \right]\)
Multiply the second row by -1 :
\(\left[ \begin{array}{ccc|c} 2 & -3 & 1 & 2 \\ 0 & 1 & 0 & 8/7 \\ 0 & 0 & 1 & 2/7 \end{array} \right]\)
Eliminate y and z from the first row by combining 3 (row 2), -1 (row 3), and row 1 :
\(\left[ \begin{array}{ccc|c} 2 & 0 & 0 & 36/7 \\ 0 & 1 & 0 & 8/7 \\ 0 & 0 & 1 & 2/7 \end{array} \right]\)
Multiply the first row by 1/2 :
\(\left[ \begin{array}{ccc|c} 1 & 0 & 0 & 18/7 \\ 0 & 1 & 0 & 8/7 \\ 0 & 0 & 1 & 2/7 \end{array} \right]\)
Use the drawing tool(s) to form the correct answer on the provided graph.
A dilation by a scale factor of 2 centered at (2,-1) is performed on the triangle shown.
Draw the resulting triangle.
Drawing Tools
Select
Point
Line Segment
Click on a tool to begin drawing.
<+++
-10 -9 -8-7 -6 -5
-4
-2
10
9-
8-
7+
6
5-
4-
3-
2-
1
Delete
3
5
Undo
6
7
00
8
Reset
9 10 no

Answers
The resulting dilated triangle is as attached and it has the coordinates; (2, 4), (4, -2) and (-6, -2).
How to interpret Dilation Scale Factor?When a triangle is dilated, it means that each vertex of the figure has it's coordinates multiplied by the scale factor of the dilation. Now, due to the fact that multiplication operation is involved, it means that the original triangle and the dilated triangle are not congruent, as their side lengths are different.
The vertices of the triangle are given as follows:
(1, 2), (2, -1) and (-3, -1).
The dilation has a scale factor of 2, meaning that each coordinate of the vertices will be multiplied by 2 and as such, the coordinates of the dilated triangle are given as follows:
(2, 4), (4, -2) and (-6, -2).
The new triangle is as attached
Read more about dilation scale factor at; https://brainly.com/question/10253650
#SPJ1

You pay $947.60 a year in car insurance. the insurance is paid in four equal payments. Find the amount of each payment.
Answers
Answer:
$236.90
Step-by-step explanation:
947.60 / 4 = 236.90
a rectangular pen is built with one side against a barn. if 2500 m of fencing are used for the oterh three sides of the pen, what dimensions maximizze the area of the pen
Answers
The dimensions that maximize the area of the pen are 1250 meters parallel to the barn and 625 meters perpendicular to the barn on both sides.
To maximize the area of a rectangular pen built with one side against a barn, you must determine the optimal dimensions for the other three sides, given a fixed amount of fencing (2500 meters). Let's denote the length of the pen parallel to the barn as "x" meters and the length of the two other sides perpendicular to the barn as "y" meters each. Since we have 2500 meters of fencing, we can express this constraint as:
x + 2y = 2500
We need to maximize the area (A) of the pen, which is given by the product of its dimensions:
A = xy
To solve this problem, we can express "y" in terms of "x" using the constraint equation:
y = (2500 - x) / 2
Now, substitute this expression for "y" into the area formula:
A = x * (2500 - x) / 2
Simplifying the equation, we get:
A = -x^2 / 2 + 2500x / 2
To find the maximum area, we must determine the value of "x" that maximizes the function A(x). To do this, we take the derivative of A(x) with respect to x and set it equal to zero:
dA/dx = -x + 2500/2 = 0
Solving for "x," we find that x = 1250 meters. Using the constraint equation, we can calculate "y" as:
y = (2500 - 1250) / 2 = 625 meters
Thus, the dimensions are 1250 meters parallel to the barn and 625 meters perpendicular to the barn on both sides.
To know more about maximum area, refer to the link below:
https://brainly.com/question/9560058#
#SPJ11
Which one is a function brainliest will be involved:)

Answers
Answer:
4th one because all the x values are different
Step-by-step explanation:
Dady ahahahdhdhsms d
Answers
Answer:
Do you need help or something??
Step-by-step explanation:
Can you pls help me with this question thank you

Answers
Part 1
we have the formula
\(F=\frac{9}{5}C+32\)so
Poconos NY C=15 degrees
substitute in the formula
\(\begin{gathered} F=\frac{9}{5}(15)+32 \\ F=27+32 \\ F=59^o \end{gathered}\)Canada, C=5
substitute
\(\begin{gathered} F=\frac{9}{5}(5)+32 \\ F=9+32 \\ F=41^o \end{gathered}\)Part II
Holiday Inn ------> 80n+10
Days Inn ------> 110n-50
Part III
For n=3
substitute in each expression
Holiday Inn -----> 80(3)+10=$250
Days Inn ------> 110(3)-50=$280
therefore
The cheaper hotel is Holiday Inn
Part IV
Holiday Inn -----> cheaper hotel
Canada ----> the temperature is less than NY
therefore
Erik should go to Canada, to the Holiday Inna class has 10 boys and 12 girls. 3 students are chosen at random to clean the classroom each day. how many unique cleaning teams exist?
Answers
The number of different unique cleaning teams should be 1540.
What are permutation and combination?A permutation is an arrangement of things where order matters, AB and BA are two different permutations.
The combination is a selection of things where order does not matter, AB and BA are the same combinations.
Given, A class has 10 boys and 12 girls and 3 students are chosen at random.
So, the team of 3 can be chosen as 3 boys, 3 girls, 1 boy 2 girls, and 1 girl and 2 boys and the total teams will be the sum of different combinations which is,
= \(^{10}C_3 + ^{12}C_3 + ^{10}C_1\times^{12}C_2 + ^{12}C_1\times^{10}C_2\).
= (10×9×8)/6 + (12×11×10)/6 + 10×(12×11)/2 + 12×(10×9)/2.
= 120 + 220 + 660 + 540.
= 1540.
learn more about permutation and combination here :
https://brainly.com/question/28720645
#SPJ1
Colin leaves school to go home. He walks 3 blocks south and then 9 blocks west. If Colin could walk in a straight line to the school, what is the exact distance between Colin and the school?
Answers
Answer:
9.48*
Step-by-step explanation:
This is a right triangle. The formula for solving the Hypotenuse, or the longest side of the right triangle is A^2 + B^2 = C^2. If we put the numbers from the problem into the formula this is what we get :
3^2 + 9^2 = C^2
9 + 81 = C^2
90 = C^2
9.48 = C
* This is rounded, the exact number is closer to 9.486832980505138. Your class should tell you what to round to.
Answer:
The answer would be A. 3√10 blocks
Step-by-step explanation:
I have had this question and its 3√10 blocks.
Hope this helps you other people :))
what equation has the same solution as x^2-16x+20=-2
Answers
The equation that has the same solution as x² - 16x + 20 = -2 is x² - 16x + 22 = 0.
How did we arrive at this assertion?To find an equation with the same solution as the equation x² - 16x + 20 = -2, manipulate the given equation while preserving its solutions.
Starting with the given equation:
x² - 16x + 20 = -2
Move the constant term (-2) to the other side:
x² - 16x + 20 + 2 = 0
Simplifying:
x^2 - 16x + 22 = 0
Therefore, the equation that has the same solution as x² - 16x + 20 = -2 is x² - 16x + 22 = 0.
learn more about equation: https://brainly.com/question/22688504
#SPJ1
To relate two fields in a one-to-many
relationship, you connect them using a
a) data type
b) subdatasheet
c) common field
• d) field key
Answers
To relate two fields in a one-to-many relationship using a common field. Then the correct option is C.
You require a common field that is present in both tables in order to connect two fields in a one-to-many relationship. Data may be transferred between the two tables thanks to this shared field, which serves as a connection between them.
If you had a Customers table and an Orders table, for instance, you might link the two tables using a common column like CustomerID. Both tables would have the CustomerID column, allowing you to get all orders linked to a certain customer.
Thus, the correct option is C.
More about the function link is given below.
https://brainly.com/question/5245372
#SPJ1
is 121,196,24 and 12 rational numbers or irrational numbers
Answers
Answer:
Its a rational number
John has a ten-dollar bill. He buys a can of pop for $1.29 and 2 candy bars at.89 each. How much does he spend? How much change does he get back?
Answers
John spends $3.07
John gets as his change $6.93
John has a ten dollar bill
He buys a pop for $1.29
He also buys 2 candy bars at $0.89
= 0.89×2
= 1.78
The amount he spends
= 1.29 + 1.78
= 3.07
He spends $3.07
The amount of change he gets can be calculated as follows
10-3.07
= $6.93
Hence John spends $3.07 and gets $6.93 as his change
Read more here
https://brainly.com/question/10946606?referrer=searchResults
#SPJ1
Billy’s Boat Rentals charges a yearly fee of $105 and $9.50 each time a member wants to rent a boat. Lisa’s Boat Rentals does not charge a yearly fee but charges $14.75 every time a member rents a boat. How many times does a person have to rent a boat for Billy’s and Lisa’s to cost the same amount?
Answers
Answer:
20 times
Step-by-step explanation:
The equation is...
9.5x+105=14.75x
105=5.25x
20=x
The triangle with vertices at l space open parentheses minus 2 comma space 5 close parentheses comma e space open parentheses 1 comma space 4 close parentheses comma and d space open parentheses 2 comma space minus 2 close parentheses is translated 4 units left, 3 units up, and then reflected over the line y equal 4 to form the image triangle l apostrophe e apostrophe d apostrophe. Which vertex of the image is the greatest distance from the origin?.
Answers
The greatest distance from the origin is 10, which corresponds to vertex L'' (6, 8) of the image triangle.
To determine the vertex of the image triangle that is the greatest distance from the origin, we need to follow the given transformations step by step and find the coordinates of the image vertices.
1. Translation: The given triangle is translated 4 units left and 3 units up.
- Vertex L' is located at (-2 - 4, 5 + 3) = (-6, 8).
- Vertex E' is located at (1 - 4, 4 + 3) = (-3, 7).
- Vertex D' is located at (2 - 4, -2 + 3) = (-2, 1).
2. Reflection: The translated triangle is reflected over the line y = 4.
- The line y = 4 acts as a mirror. The y-coordinate of each vertex remains the same, but the x-coordinate is reflected.
- Vertex L'' is located at (-(-6), 8) = (6, 8).
- Vertex E'' is located at (-(-3), 7) = (3, 7).
- Vertex D'' is located at (-(-2), 1) = (2, 1).
Now, we have the coordinates of the image triangle vertices: L'' (6, 8), E'' (3, 7), and D'' (2, 1).
To determine which vertex is the greatest distance from the origin (0, 0), we can calculate the distances using the distance formula:
- Distance from the origin to L'': √[(6 - 0)² + (8 - 0)²] = √(36 + 64) = √100 = 10.
- Distance from the origin to E'': √[(3 - 0)² + (7 - 0)²] = √(9 + 49) = √58.
- Distance from the origin to D'': √[(2 - 0)² + (1 - 0)²] = √(4 + 1) = √5.
Therefore, the greatest distance from the origin is 10, which corresponds to vertex L'' (6, 8) of the image triangle.
learn more about triangles here:
https://brainly.com/question/2773823
#SPJ11
a random sample of 15 hourly fees for car washers (including tips) was drawn from a normal population. the sample mean and sample standard deviation were sample mean is $14.9 and sample standard deviation is $6.75. w e want to infer at the 5% significance level that the mean fee for car washers (including tips) is greater than 12. what is the rejection region to test the hypothesis?
Answers
The rejection region is t > 1.761.
To test the hypothesis that the mean fee for car washers (including tips) is greater than $12, we can perform a one-sample t-test.
Sample mean \(\bar{x}\) = $14.9
Sample standard deviation (s) = $6.75
Sample size (n) = 15
Significance level (α) = 0.05 (5%)
Since the sample size is small (n < 30) and the population standard deviation is unknown, we will use the t-distribution for inference.
Define the null and alternative hypotheses:
Null hypothesis (H₀): μ ≤ $12 (Mean fee for car washers is less than or equal to $12)
Alternative hypothesis (H₁): μ > $12 (Mean fee for car washers is greater than $12)
Determine the critical value (rejection region) based on the significance level and degrees of freedom.
The degrees of freedom (df) for a one-sample t-test is calculated as df = n - 1 = 15 - 1 = 14.
Using a t-table or statistical software, we find the critical t-value for a one-tailed test with α = 0.05 and df = 14 to be approximately 1.761.
Calculate the test statistic:
The test statistic for a one-sample t-test is given by:
t = (\(\bar{x}\) - μ) / (s / √n)
Plugging in the values:
t = ($14.9 - $12) / ($6.75 / √15) ≈ 2.034
Make a decision:
If the test statistic t is greater than the critical t-value, we reject the null hypothesis. Otherwise, we fail to reject the null hypothesis.
In this case, the calculated t-value (2.034) is greater than the critical t-value (1.761), indicating that it falls in the rejection region.
State the conclusion:
Based on the test results, at the 5% significance level, we have enough evidence to reject the null hypothesis.
We can infer that the mean fee for car washers (including tips) is greater than $12.
For similar question on rejection region.
https://brainly.com/question/27963477
#SPJ11
Suppose that A and B are independent events with P(A)=0.9 and P(B)=0.5. (a) If the Asian project is not successful, what is the probability that the European project is also not successful? ]∗ Explain your reasoning. Since the events are independent, then A ′
and B ′
are independent. Since the events are not independent, then A ′
and B ′
are mutually exclusive. Since the events are independent, then A ′
and B ′
are mutually exclusive. Since the events are independent, then A ′
and B ′
are not independent. (b) What is the probability that at least one of the two projects will be successful? (c) Given that at least one of the two projects is successful, what is the probability that only the Asian project is successful? (Round your answer to three decimal places.)
Answers
The probability that the European project is not successful given that the Asian project is not successful is 1., the probability that at least one project is successful is 1 - (1 - P(A)) * (1 - P(B)).
Since A and B are independent events, the outcome of one event does not affect the outcome of the other. Therefore, if the Asian project is not successful (A'), it does not provide any information about the success or failure of the European project (B').
To understand this, let's consider the definition of independent events. Two events A and B are considered independent if the occurrence or non-occurrence of one event does not affect the probability of the other event occurring or not occurring.
In this case, A and B are independent events. So, the probability of A' (not successful Asian project) does not provide any information about the probability of B' (not successful European project). Therefore, the probability that the European project is not successful given that the Asian project is not successful is 1, as it is not affected by the outcome of the Asian project.
(b) The probability that at least one of the two projects will be successful can be calculated by finding the complement of the probability that both projects fail. Since A and B are independent events, the probability that both projects fail is P(A') * P(B') = (1 - P(A)) * (1 - P(B)). Therefore, the probability that at least one project is successful is 1 - (1 - P(A)) * (1 - P(B)).
(c) Given that at least one of the two projects is successful, the probability that only the Asian project is successful can be calculated by finding the probability of A and not B, which is P(A) * (1 - P(B)). This represents the probability of the Asian project being successful while the European project is not.
Learn more about probability here:
brainly.com/question/31828911
#SPJ11
The size of an interior door frame is determined by the width of the wall into which it is installed. The width of the wall is determined by the width of the stud in the wall and the thickness of the sheets of drywall installed on each side of the wall. A 2 * 4 studs is 5/8 inches thick. A 2 * 6 studs is 5 5/8 inches thick.Find the difference in thickness between a fire wall constructed with 2 * 6 studs and drywall that is 3/4 inch thick and a fire wall constructed with 2 * 4 studs and drywall that is 5/8 inch thick.

Answers
To solve this exercise we only need to find the difference in thickness between the 2 walls
wall one• Drywall = 3/4 inch thick
,• Stud 2x6 =5 5/8 inch thick
\(\begin{gathered} Wall_1=\frac{3}{4}+5\frac{5}{8}+\frac{3}{4} \\ Wall_1=\frac{3}{4}+5+\frac{5}{8}+\frac{3}{4} \\ Wall_1=\frac{57}{8} \end{gathered}\)wall two• Drywall = 5/8 inch thick
,• Stud 2x4=3 5/8 inch thick
\(\begin{gathered} Wall_2=\frac{5}{8}+3\frac{5}{8}+\frac{5}{8} \\ Wall_2=\frac{5}{8}+3+\frac{5}{8}+\frac{5}{8} \\ Wall_2=\frac{39}{8} \end{gathered}\)We proceed to subtract them to know what the difference is
\(\begin{gathered} Wall_1=\frac{57}{8} \\ Wall_2=\frac{39}{8} \end{gathered}\)\(Difference=Wall_1-Wall_2\)\(\begin{gathered} Difference=\frac{57}{8}-\frac{39}{8} \\ Difference=\frac{57-39}{8} \\ Difference=\frac{18}{8} \\ Difference=\frac{9}{4} \\ Difference=2.25 \end{gathered}\)The 2 walls differ by 9/4 inch or 2.25inch. Wall one is thicker than Wall twoThe least preferable and reliable method of selecting people to participate in a research study is:_____.
Answers
The least preferable and reliable method of selecting people to participate in a research study is convenience sampling.
Convenience sampling is a type of sampling in which you include people who are easy to reach. Convenience sampling is included in non-probability sampling because it doesn't include a random selection of the participants. Convenience sampling can be used when you need to conduct a study quickly or when you are on a shoestring budget as it is inexpensive compared to other methods of sampling.
It is the least preferable method because of the inability to generalize the result of the survey to the population as a whole. In addition to this, there is a possibility of under or over-representation of the population as a whole. The biggest problem with convenience sampling is dependence as the sample items are connected to each another in some way. This dependency interferes with statistical analysis.
To learn more about convenience sampling, click here:
https://brainly.com/question/5997269
#SPJ4
welp i need help 20 points
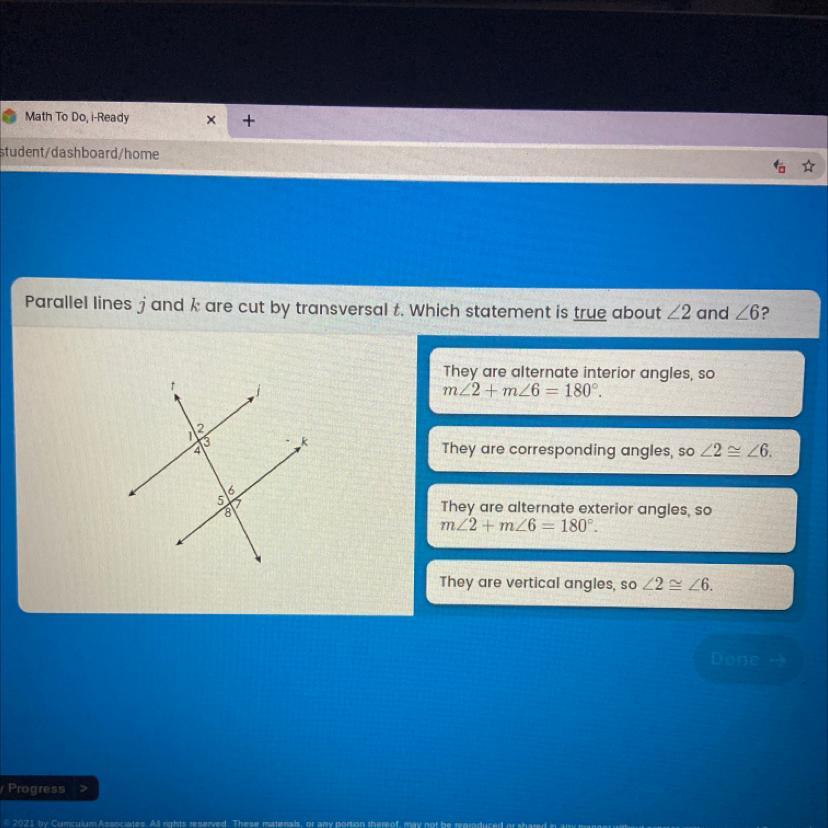
Answers
Answer:
The 3rd one
Step-by-step explanation:
Answer:
They are corresponding angles
Step-by-step explanation:
If this answer helped you then please consider marking this as brainliest and like this respone :)
given A and b to the right, write the augmented matrix for the linear system that corresponds to the matrix equation Ax = b. Then solve the system and write the solution as a vector
[ 1 3 -4 ] [ -13 ]
A = [ 2 5 2 ] b = [ 11 ]
[ 3 2 5 ] [ 8 ]
Answers
1 & -1 & 2
The augmented matrix for the linear system corresponding to the matrix equation Ax = b, where A is the given matrix and b is the given vector, is
$\begin{bmatrix}
1 & 3 & -4 & -13 \\
2 & 5 & 2 & 11 \\
3 & 2 & 5 & 8
\end{bmatrix}$
Solving the system yields the vector solution
$\begin{bmatrix}
1 & -1 & 2
\end{bmatrix}$
Learn more about augmented matrix
brainly.com/question/28832583
#SPJ11
how to find the proportion of adjustable/ fixed ratios
Answers
To find the proportion of adjustable/ fixed ratios, you will need to divide the number of adjustable items by the total number of items. For example, if you have 8 adjustable items and 10 total items, the proportion of adjustable items is 8/10, or 0.8.
To find the proportion of adjustable/fixed ratios, you need to follow these steps:
1. Identify the adjustable and fixed ratios in the question.
2. Convert the adjustable and fixed ratios into fractions.
3. Find the common denominator of the two fractions.
4. Multiply both the numerator and denominator of each fraction by the common denominator.
5. Subtract the numerator of the fixed ratio fraction from the numerator of the adjustable ratio fraction.
6. Simplify the resulting fraction if necessary.
For example, if you have an adjustable ratio of 2:3 and a fixed ratio of 1:4, you would first convert these ratios into fractions, 2/3 and 1/4. Next, you would find the common denominator, which is 12. You would then multiply both the numerator and denominator of each fraction by 12, resulting in 8/12 and 3/12. Finally, you would subtract 3 from 8 to get 5, and simplify the resulting fraction to 5/12. Therefore, the proportion of the adjustable/fixed ratios is 5/12.
Know more about proportion here:
https://brainly.com/question/870035
#SPJ11
What is the area of B

Answers
If there is no more informations, then:
A = ¹/₃(6 + x)Find the value of each trigonometric ratio. 1) sin X 28 Z 21
Answers
Answer:
.
Step-by-step explanation:
I also need to show calculations for each side length plz help

Answers
Answer:
WO \(\sqrt{13}\ \ \ \frac{3}{2}\)
OR \(\sqrt{13}\ \ \ - \frac{3}{2}\)
RM \(\sqrt{13}\ \ \ \frac{3}{2}\)
MW \(\sqrt{13}\ \ \ - \frac{3}{2}\)
Step-by-step explanation:
One has to find the slope, and the distance between the successive points on the plane. Use the slope and distance formula to achieve this.
Slope formula:
\(\frac{y_2-y_1}{x_2-x_1}\)
Distance formula:
\(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\)
Remember, the general format for the coordinates of a point on a Cartesian coordinate plane is the following:
\((x,y)\)
1. WO
Coordinates of point (W): (3, -5)
Coordinates of point (O): (6, -3)
Find the slope:
\(\frac{y_2-y_1}{x_2-x_1}\)
\(\frac{(-5)-(-3)}{(3)-(6)}=\frac{-5+3}{3-6}=\frac{-2}{-3}=\frac{2}{3}\)
Find the distance:
\(\sqrt{((-5)-(-3))^2+((3)-(6))^2}\)
\(\sqrt{(-2)^2+(-3)^2}\\=\sqrt{4+9}\\=\sqrt{13}\\\)
2. OR
Coordinates of point (O): (6, -3)
Coordinates of point (R): (4, 0)
Find the slope:
\(\frac{y_2-y_1}{x_2-x_1}\\=\frac{(0)-(-3)}{(4)-(6)}=\frac{3}{-2}=-\frac{3}{2}\)
Find the distance:
\(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
\(\sqrt{((0)-(-3))^2+((4)-(6))^2}=\sqrt{(3)^2+(2)^2}=\sqrt{9+4}=\sqrt{13}\)
3. RM
Coordinates of point (R): (4, 0)
Coordinates of point (M): (1, -2)
Find the slope:
\(\frac{y_2-y_1}{x_2-x_1}\\=\frac{(0)-(-2)}{(4)-(1)}=\frac{2}{3}\)
Find the distance:
\(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
\(\sqrt{((-2)-(0))^2+((1)-(4))^2}=\sqrt{(-2)^2+(-3)^2}=\sqrt{4+9}=\sqrt{13}\)
4. MW
Coordinates of point (M): (1, -2)
Coordinates of point (W): (3, -5)
Find the slope:
\(\frac{y_2-y_1}{x_2-x_1}\)
\(=\frac{(-5)-(-2)}{(3)-(1)}=\frac{-3}{2}=-\frac{3}{2}\)
Find the distance:
\(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
\(=\sqrt{((3)-(1))^2+((-5)-(-2))^2}=\sqrt{(2)^2+(3)^2}=\sqrt{4+9}=\sqrt{13}\)
A car is traveling at 55 mph. What is the
speed of the car in feet per second (ft/s)?
Answers
Answer:
80 feet per second
Step-by-step explanation: At 55 mph, your vehicle is traveling at about 80 feet per second. Feet-per-second is determined by multiplying speed in miles-per-hour by 1.47 (55 mph x 1.47 = 80 feet per second.)