Use elimination to solve for x and y:
9x - 4y = 11
x + 4y = 19
Select one:
a. (7,3)
b. (4,3)
c. (-1,5)
d. (3,4)

Using the interpretation of a confidence interval, it is found that approximately 950 of those confidence intervals will contain the value of the unknown parameter.

A x% confidence interval means that we are x% confident that the population mean is in the interval.

In this problem:

0.95 x 1000 = 950

Hence, approximately 950 of those confidence intervals will contain the value of the unknown parameter.

A similar problem is given at https://brainly.com/question/24303674

Step-by-step explanation:

The vertical line exactly between them     x = -1   is the axis of rotation

Answer:

The rates are not equivalent since Maria saves $0.50 more per month than Ralph.

Step-by-step explanation:

We can determine if two rates are equivalent by comparing the rates at which they save per month.

Maria's savings per month:

Both 50 and 4 can be divided by 2, which gives us 25/2.  As a regular number, this becomes 12.5/1 which means Maria saves $12.5 per month.

Ralph's savings per month:

Both 60 and 5 can be divided by 5, which gives us 12.  Thus, Ralph saves $12 per month.

Thus, the rates are not equivalent as Maria saves $0.50 more per month than Ralph.

Answer:

Mean (Average) = -23.5

Median = -26.5

Mode = -28

Range = 52

Step-by-step explanation:

Mean is found when adding all numbers and dividing the outcome by the number of numbers, so -

-11 + -28 + -17 + -25 + -28 + -39 + 6 + -46 = -188

-188 ÷ 8 = -23.5

Median is found in the center, and can be found ordered from least to greatest -

-46, -39, -28, -28, -25, -17, -11, 6

last 2 remaining number would be -28 and -25, add those and divide by 2 which gives you -26.5.

The Median would be -26.5

Mode is the number that has repeated itself the most.

-28 repeated itself the most.

The Range is found when the least number is subtracted by the greatest number so -

6 - (-46) = 52

Answer:

the answer is in the picture

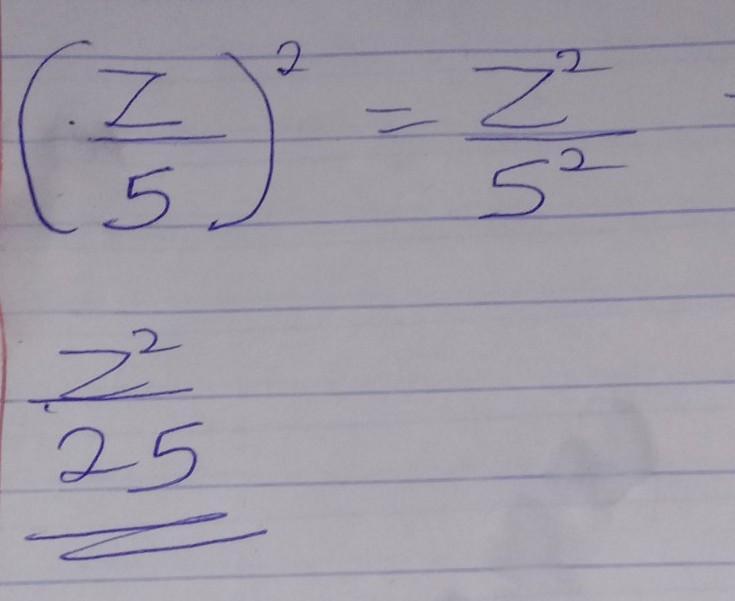
Answer:

\(\frac{z^{2} }{25}\)

Step-by-step explanation:

In order to write the expression in the form of \(\frac{z^{2} }{k}\) we simply have to open up the brackets. We do that the following way...

\((\frac{z}{5} )^{2} =( \frac{z}{5} )( \frac{z}{5}) = \frac{z^{2} }{25}\)

Answer:

The correct answer is option B

Answer:

45 km por galón

60 galones en 2700 Km

Step-by-step explanation:

180 / 4

45 km por galón

900 / 45

20 galones

2700 / 45

60 galones en 2700 Km

Answer:

1. True

2. False

3. True

4. True

5. True

The x-intercepts of the given equation 4x^2-12x+4 is -3/2

What is Quadratic equation ?

Quadratic equation can be defined as the equation in which it is in the form of ax^2+bx+c = 0

where c is a constant.

Given equation ,

y = 4x^2+12x+4

so we have to find the x-intercept , make y = 0

and we have to solve for the given quadratic equation

so,

we get

4x^2+12x+4 = 0

(2x)^2 + 9 + 12x = 0

(2x+3)^2 = 0

x = -3/2

There is double root unique intercept or tangent at  x  = -3/2

Therefore, The x-intercepts of the given equation 4x^2-12x+4 is -3/2

To learn more about Quadratic equation from the given link.

https://brainly.com/question/30098550

#SPJ1

The x axis is labeled as Number of days.

Graph is a mathematical representation of a network and it describes the relationship between lines and points.

let x be the  number of days and y be money.

So, the equation is

y = -7x + 150.

Hence, the x axis is labeled as Number of days.

Learn more about this concept here:

https://brainly.com/question/1509203

#SPJ1

Answer:

First Equation is Right which is -56/8 = 7

Step-by-step explanation:

LHS = -56/8

=> -7

RHS = -7

So LHS = RHS

Answer:

the first one. -56/8 = -7

Answer:

Step-by-step explanation:

19 cups of rice

The number of cups of rice that can be cooked with 29 cups of water will be 19 cups.

The allocation of weights to the important variables that produce the calculation's optimum is referred to as a direct consequence.

The definition of simplicity is making something simpler to achieve or grasp while also making it a little less difficult.

Here is a formula for the amount of water needed to cook rice. w = 1.5r + 0.5

Where 'w' is the number of cups of water needed 'r' is the number of cups of rice to be cooked.

The number of cups of rice that can be cooked with 29 cups of water will be given as,

29 = 1.5r + 0.5

1.5r = 28.5

r = 19

The number of cups of rice that can be cooked with 29 cups of water will be 19 cups.

More about the solution of the equation link is given below.

https://brainly.com/question/545403

#SPJ5

The matrix representation of the problem can be written as: ε = [ε1 ε2 ε3]'

The matrix representation of the linear regression problem can be expressed as Y = Xβ + ε, where Y is the n x 1 vector of the dependent variable (Yi),

X is the n x k matrix of the independent variables (xi),

β is the k x 1 vector of coefficients, and

ε is the n x 1 vector of errors.

In this case, n = 3 (number of observations), k = 2 (number of independent variables) and the matrix representation of the problem can be written as:

Y = Xβ + ε

Y = [0.3 0.8 -0.3]

X = [1 1 1; 1 2 0.1]

β = [β0 β1]'

ε = [ε1 ε2 ε3]'

For more questions on Matrix representation

https://brainly.com/question/13594851

#SPJ4

Answer:

The ratio for the first print job is 150/30 = 5 pages per second.

The ratio for the second print job is 130/20 = 6.5 pages per second.

Since the ratios are different, the data do not represent a proportional relationship. In a proportional relationship, the ratio between two variables remains constant.

Step-by-step explanation:

Answer:

  θ = ±2π/3 +2kπ . . . . . for any integer k

Step-by-step explanation:

  2·cos(θ) +1 = 0

  cos(θ) = -1/2 . . . . . subtract 1, divide by 2

The cosine function has the value -1/2 for θ = ±2π/3 and any integer multiple of 2π added to that.

  θ = ±2π/3 +2kπ . . . . . for any integer k

Considering the definition of percent of error, the Stephanie’s percent of error in this case is 5.042%.

Percent of error is a measure of how inaccurate a measurement is, standardized based on the size of the measurement.

In other words, the percent of error allows knowing the differences between the estimated value and the real value. The error may be due to the measurement method (tool or human error) or due to approximations used in the calculation (for example, rounding errors).

To calculate the percent of error you must:

Therefore, the expression for calculating the percent of error is

percent of error= [|real value - estimated value|÷ real value]×100

In this case, you know:

Replacing in the definition of percent of error:

percent of error= [|8.33 pounds - 8.75 pounds|÷ 8.33 pounds]×100

Solving;

percent of error= [|-0.42 pounds|÷ 8.33 pounds]×100

percent of error= [0.42 pounds÷ 8.33 pounds]×100

percent of error= 0.05042×100

percent of error= 5.042%

Finally, the percent of error in this case is 5.042%.

Learn more about percent of error:

https://brainly.com/question/26090711

https://brainly.com/question/26668346

https://brainly.com/question/28780110

#SPJ1

Answer:

\(P(9,3) *P(5,4)\)

And if we use the permutation formula given by:

\( nPx = \frac{n!}{(n-x)!}\)

And replacing we got:

\( \frac{9!}{6!} \frac{5!}{4!}= 504*5 = 2520\)

Step-by-step explanation:

For this problem we want to find the following expressionÑ

\(P(9,3) *P(5,4)\)

And if we use the permutation formula given by:

\( nPx = \frac{n!}{(n-x)!}\)

And replacing we got:

\( \frac{9!}{6!} \frac{5!}{4!}= 504*5 = 2520\)

Answer:

1.3 m²

Step-by-step explanation:

The shape is a trapezoid.

Area of a trapezoid = ½(a + b)*h

Where, a = 0.8 m

b = 1.8 m

h = height of the trapezoid which is not given.

Therefore, find h using trigonometric function with 45° as reference angle:

Hypotenuse = 1.4 m

Opposite = h

Apply SOH, which is:

Sin 45 = Opp/Hyp

Sin 45 = h/1.4

1.4*Sin 45 = h

0.989949493 = h

h ≈ 1.0 m

✔️Area of Trapezoid = ½(0.8 + 1.8)*1 = 1.3 m²

Answer:

Step-by-step explanation

Given

a snail moves through a garden and travels 1 1/8 meters in 1 1/2 Minutes.

Solution

So

the snails rate =11/8÷11/2

= 1/4Minutes per Meters

So the answer is 1/4 minute per meter

It is the quantity of an amount of something at a rate of one of another quantity.

If a snail moves through a garden and travels 1 1/8 meters in 1 1/2 Minutes.

The snail's rate in minutes per meter is 4/3 minutes.

It is the quantity of an amount of something at a rate of one of another quantity.

Example:

3 miles in 60 minutes.

1 mile in 20 minutes.

We have,

Snail travels:

\(1\frac{1}{8}\) meters = \(1\frac{1}{2}\) minutes

9/8 meters = 3/2 minutes

Multiplying 8/9 on both sides.

1 meters = 8/9 x 3/2 minutes

1 meter = 4/3 minutes

This means that the snail's rate in minutes per meter is 4/3 minutes.

Thus,

If a snail moves through a garden and travels 1 1/8 meters in 1 1/2 Minutes.

The snail's rate in minutes per meter is 4/3 minutes.

Learn more about unit rates here:

https://brainly.com/question/11258929

#SPJ5

The length of a 45° arc with a radius of 4 miles is approximately 3.14 miles, calculated using the formula for arc length.

To determine the length of a 45° arc given a radius of 4 miles, we can use the formula: Arc length = (angle measure / 360°) x 2πr, where r is the radius of the circle and π is a constant equal to approximately 3.14.

Substituting the given values into the formula, we get: Arc length = (45° / 360°) x 2π(4 mi)Arc length = (1/8) x 2π(4 mi)Arc length = (1/8) x 8π Arc length = π

The length of the 45° arc is approximately 3.14 miles.

Summary: To find the length of a 45° arc of a circle, we use the formula: Arc length = (angle measure / 360°) x 2πr. Given a radius of 4 miles, we can substitute the values into the formula to get the length of the 45° arc, which is approximately 3.14 miles.

For more questions on arc length

https://brainly.com/question/31341388

#SPJ8

The solution to the system of equations y = 1/8x −1 and −5x + 4y = −13 is (2, −3/4). Option D is correct.

We are given:

y = 1/8 x − 1                 ..............equation i.

− 5x + 4y = − 13          ..............equation ii.

We will use the substitution method to solve the given equation.

substitute the value of y from equation i in equation ii, and we will get;

− 5x + 4(1/8 x − 1) = − 13

− 5x + 1/2 x − 4 = − 13

(-10 + 1) / 2 x = -13 + 4

-9/2 x = -9

x = -9 * 2 / -9

x = 2

Put the value of x in equation i, we will get;

y = 1/8 *2 − 1

y = 1/4 - 1

y = 1 - 4 / 4

y = -3 / 4

So, the value of x = 2 and the value of y = -3 / 4.

Thus, the solution to the system of equations y = 1/8x −1 and −5x + 4y = −13 is (2, −3/4). Option D is correct.

To learn more about substitution method visit:

https://brainly.com/question/14619835

#SPJ1

To find the distance between points A and B, we can use trigonometry and the given information.

Let's label the distance between A and B as "d". We know that point C is 94.4 meters away from point A. From angle A, we have the measure of 72°, and from angle C, we have the measure of 30°.

Using trigonometry, we can use the tangent function to find the value of "d".

tan(72°) = d / 94.4

To solve for "d", we can rearrange the equation:

d = tan(72°) * 94.4

Using a calculator, we can evaluate the expression:

d ≈ 4.345 * 94.4

d ≈ 408.932

Therefore, the distance between points A and B is approximately 408.932 meters.

The water Ms. Morales put in the pool in terms of π is  \(\pi\)6561inch^3

Suppose that the radius of considered right circular cylinder be 'r' units.

And let its height be 'h' units.

Then, its volume is given as:

\(V = \pi r^2 h \: \rm unit^3\)

Right circular cylinder is the cylinder in which the line joining center of top circle of the cylinder to the center of the base circle of the cylinder is perpendicular to the surface of its base, and to the top.

Given;

Diameter= 54 in.

Height of pool= 12ft

Now,

3/4 th height of pool;

3/4 x 12= 9inch

Volume= \(\pi r^{2}h\)

=\(\pi\)27x27x9

=\(\pi\)6561inch^3

Therefore, the volume of pool will be \(\pi\)6561inch^3

Learn more about volume of cylinder here:

https://brainly.com/question/12763699

#SPJ1

A graph which represents the number of outfits and shoes that Alejandra can pack while staying under the weight limit is shown in the image attached below.

A graph can be defined as a type of chart that's commonly used to graphically represent data on both the horizontal and vertical lines of a cartesian coordinate, which are the x-axis and y-axis.

In this scenario, the x-axis represents the number of outfits while the y-axis represents the number of shoes. Additionally, since one pair of shoes weighs three (3) pounds and one outfit weighs two (2) pounds, the x and y coordinates would be given by this inequality:

2x + 3y < 30

Making y the subject of formula, we have:

3y < -2x + 30

Dividing all through by 3, we have:

3y/3 < -2x/3 + 30/3

y < -2x/3 + 10

Note: For 30 pounds, there would be 10 shoes (0, 10) while for 30 pounds, there would be 15 outfits (15, 0).

In conclusion, the boundary line is dashed or dotted to indicate that the boundary is not part of the solution because the inequality symbol is less than (<).

Read more on graphs here: brainly.com/question/4546414

#SPJ1

The general solution of the partial differential equation is:

U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)

The partial differential equation (PDE) is given as:

Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)

Assume that the solution can be written as a product of two functions:

U(x, t) = X(x)T(t)

Substituting this into the PDE, we have:

X''(x)T(t) = (1/2)X(x)T'(t)

Dividing both sides by X(x)T(t), we get:

(X''(x))/X(x) = (1/2)(T'(t))/T(t)

Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:

(X''(x))/X(x) = -λ²

(1/2)(T'(t))/T(t) = -λ²

Simplifying the second equation, we have:

T'(t)/T(t) = -2λ²

Solving the second equation, we find:

T(t) = Ce^(-2λ²t)

Applying the boundary condition U(0, t) = 0, we have:

U(0, t) = X(0)T(t) = 0

Since T(t) ≠ 0, we must have X(0) = 0.

Applying the boundary condition U(3, t) = 0, we have:

U(3, t) = X(3)T(t) = 0

Again, since T(t) ≠ 0, we must have X(3) = 0.

Therefore, we can conclude that X(x) must satisfy the following boundary value problem:

X''(x)/X(x) = -λ²

X(0) = 0

X(3) = 0

The general solution to this ordinary differential equation is given by:

X(x) = Asin(λx) + Bcos(λx)

Applying the initial condition U(x, 0) = 5*sin(4πx), we have:

U(x, 0) = X(x)T(0) = X(x)C

Comparing this with the given initial condition, we can conclude that T(0) = C = 5.

Therefore, the complete solution for U(x, t) is given by:

U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)

where:

Σ represents the summation over all values of n

λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).

To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):

X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0

X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0

From the first equation, we have Bₙ = 0.

From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.

This implies that 3λₙ = nπ, where n is an integer.

Therefore, λₙ = (nπ)/3.

Substituting the eigenvalues into the general solution, we have:

U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)

where Aₙ are the coefficients that can be determined from the initial condition.

Read more about Partial Differential Equations at: https://brainly.com/question/28099315

#SPJ1

Answer:

205 sec

Step-by-step explanation:

x = sister

2x = Diana

2x = 410

x = 205

205 sec

hope this makes sense

Answer:

1.  14:9

2. 14 to 9

3. 14/9

Step-by-step explanation:

Answer:

9^1 has a power of 1.  it evaluates to 9

Step-by-step explanation:

The given function y = 2(x² - 1) is decreasing for all values in the domain and it has a horizontal asymptote along the x-axis so options (B) and (C) will be correct.

A certain kind of relationship called a function binds inputs to essentially one output.

The nature of the relationship between the variables that makes up a function, such as y = sinx and y = x +6, defines the function.

Given the function,

y = 2(x² - 1)

If we increase the value of x to positive then the denominator x² - 1 will go to increase and thus y will decrease.

If we increase the value of x in negative then denominator x² - 1 will go to increase and thus y will decrease.

Therefore it is decreasing for all values in the domain.

Now,

Lim at x tends to ∞ of function is 2/∞ = 0 so y = 0 means there is a horizontal asymptote along the x-axis.

Hence "The given function y = 2(x² - 1) is decreasing for all values in the domain and it has a horizontal asymptote along the x-axis".

For more about the function,

brainly.com/question/23712366

#SPJ2

The solution to the inequality 1 + 3r > 10 is r > 3.

This means that any value of r greater than 3 will satisfy the inequality.

To solve the inequality 1 + 3r > 10, we need to isolate the variable r on one side of the inequality sign.

Let's begin by subtracting 1 from both sides of the inequality:

1 + 3r - 1 > 10 - 1

This simplifies to:

3r > 9

Next, we can divide both sides of the inequality by 3 to solve for r:

(3r)/3 > 9/3

This simplifies to:

r > 3

For similar question on inequality.

https://brainly.com/question/30604125  

#SPJ8