There are 785 people seated in a large cafeteria. Six people can sit at each table. How many tables are in the cafeteria?

4.2 x 10^8 is  2*10^6  times the value of 2.1 x 10^2 when division is performed.

The concept that will be used to solve the question is division operation.

We were given 4.2 x 10^8 which is greater than  2.1 x 10^2

The operation can be expressed as :

4.2 x 10^8 =( n *2.1 x 10^2)

where n = the number of times that 4.2 x 10^8  is greater than 2.1 x 10^2

Then make n the subject of the formular which is

n = 4.2 x 10^8/2.1 x 10^2

n = 2*10^6

Therefore, the values of 4.2 x 10^8 is greater than 2.1 x 10^2 in 2*10^6 times.

Read more about division at:

brainly.com/question/11421834

#SPJ1

Answer:

Following are the responses to the given question:

Step-by-step explanation:

Level of Significance,\(\alpha = 0.05\)

Sample Size, \(n = 120\)          

Sample Proportion,   \(\hat{P} = 0.600\)      

\(z -value = Z_{\frac{\alpha}{2}} = 1.960 \ \ [excel formula =NORMSINV(\frac{\alpha}{2})]\)

Standard Error\(SE = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} = 0.0447\)        

margin of error \(E = Z\times SE = 1.960 \times 0.0447 = 0.0877\)

When \(95\%\) Confidence Interval              

Interval Lower Limit\(= \hat{p} - E = 0.600 - 0.0877 = 0.5123\)

Interval Upper Limit \(=\hat{p}+ E = 0.600 + 0.0877 = 0.6877\)

Answer:

Current Ratio

Step-by-step explanation:

The current ratio is a liquidity ratio that measures how able a company is to pay short-term obligations, or current liabilities, with its current assets.

The formula is \(Current\:Ratio=\frac{Current\:Assets}{Current\:Liabilities}\)

Answer:

m<T = 88

Step-by-step explanation:

7x + 4 + 5x + 3 + 2x + 5 = 180

14x + 12 = 180

14x = 168

x = 12

<T = 7x + 4

7(12) + 4

84 + 4

88

Solution:

Your problem → x + 45 = 97x

x+45=97x

⇒-96x+45=0

⇒96x=45

⇒x=45/96

⇒x=15/32

Answer:

a=25 b=100 c=17 d=68

Step-by-step explanation:

the test said so

The length of the curve segment y = 4x^2 from x = 0 to x = 1 can be calculated by evaluating the definite double integral over the region of the x-y plane bounded by the curve y = 4x^2 and the x-axis,

The square root of the sum of the squares of the partial derivatives of x and y with respect to the arclength parameter.

To evaluate this integral, we first note that

y = 4x^2, so dy/dx = 8x.

Thus, the integral with respect to x is:

s = ∫_0^1 sqrt(1 + (8x)^2) dx

To evaluate this integral,

we can use the substitution

u = 8x,

which gives us

du = 8 dx.

Thus,

the integral becomes:

s = (1/8) ∫_0^8 sqrt(1 + u^2) du

This can be evaluated using trigonometric substitution.

Letting v = arctan(u),

we have

dv = du / sqrt(1 + u^2),

and the integral becomes:

s = (1/8) ∫_{arctan(0)}^{arctan(8)} sqrt(1 + tan^2(v)) dv

This can be evaluated using the substitution

v = tan(v),

which gives us

dv = sec^2(v) dv.

Thus, the integral becomes:

s = (1/8) ∫_0^{arctan(8)} sec(v) dv

This can be evaluated using the substitution

u = tan(v),

which gives us

du = sec^2(v) dv.

Thus, the integral becomes:

s = (1/8) ∫_0^8 1 / sqrt(1 + u^2) du

This can be evaluated using the substitution

u = sinh(v),

which gives us

du = cosh(v) dv.

Thus, the integral becomes:

s = (1/8) ∫_0^8 cosh(v) dv

This can be evaluated using the identity

cosh(v) = (exp(v) + exp(-v)) / 2,

giving us:

s = (1/8) [exp(v) / 2 - exp(-v) / 2]

evaluated from 0 to 8

Finally, evaluating this expression gives us:

s = (1/8) [exp(8) / 2 - exp(-8) / 2]

This is the length of the curve segment y = 4x^2 from x = 0 to x = 1.

For such more question on derivatives

https://brainly.com/question/30396691

#SPJ4

a. The teacher can expect the batteries to last at least 92.09 days  on minimum average.

b. The teacher will need to spend at most $49.92 on batteries for calculators over the year.

What is minimum average day?

a. The margin of error of ‡9% means that we can be 95% confident that the true average number of days the batteries will last is within 9% of the sample average. To find the minimum average number of days a teacher can expect to have the batteries last in her classroom, we subtract the margin of error from the sample average:

Minimum average = 101 - (0.09)(101) = 92.09 days (rounded to two decimal places)

Therefore, the teacher can expect the batteries to last at least 92.09 days on average.

What is spend ?

b. The total number of batteries required for the 24 TI-84 calculators is:

24 calculators x 4 batteries per calculator = 96 batteries

The total cost of the batteries will be:

96 batteries x $0.52 per battery = $49.92 (rounded to two decimal places)

Therefore, the teacher will need to spend at most $49.92 on batteries for calculators over the year, assuming all batteries need to be replaced.

To know more about margin of error, visit:

https://brainly.com/question/29081172

#SPJ1

Answer:

\(P(21<X<28)=P(\frac{21-\mu}{\sigma}<\frac{X-\mu}{\sigma}<\frac{28-\mu}{\sigma})=P(\frac{21-24}{3}<Z<\frac{28-24}{3})=P(-1<z<1.33)\)

And we can find the probability with this difference

\(P(-1<z<1.33)=P(z<1.33)-P(z<-1)\)

And using the normal standard distribution or excel we got:

\(P(-1<z<1.33)=P(z<1.33)-P(z<-1)=0.908-0.159=0.749\)

Step-by-step explanation:

Let X the random variable that represent the soft drink machine outputs of a population, and for this case we know the distribution for X is given by:

\(X \sim N(24,3)\)  

Where \(\mu=24\) and \(\sigma=3\)

We want to find this probability:

\(P(21<X<28)\)

The z score is given by:

\(z=\frac{x-\mu}{\sigma}\)

Using this formula we got:

\(P(21<X<28)=P(\frac{21-\mu}{\sigma}<\frac{X-\mu}{\sigma}<\frac{28-\mu}{\sigma})=P(\frac{21-24}{3}<Z<\frac{28-24}{3})=P(-1<z<1.33)\)

And we can find the probability with this difference

\(P(-1<z<1.33)=P(z<1.33)-P(z<-1)\)

And using the normal standard distribution or excel we got:

\(P(-1<z<1.33)=P(z<1.33)-P(z<-1)=0.908-0.159=0.749\)

Answer:

Therefore, the correct statements are A, B, and E.

Explanation:

Based on my knowledge, a vector is a quantity that has both magnitude and direction. A scalar is a quantity that has only magnitude. When a vector is multiplied by a scalar, the magnitude of the vector is multiplied by the absolute value of the scalar, and the direction of the vector is either preserved or reversed depending on the sign of the scalar.

To answer your question, we need to find the component form, magnitude, and direction of the scalar product –4⇀

.

- The component form of −4⇀

is obtained by multiplying each component of ⇀

by –4. Therefore, −4⇀

= ⟨–8, –12⟩. This means that statement A is true.

- The magnitude of −4⇀

is obtained by multiplying the magnitude of ⇀

by 4. The magnitude of ⇀

is √(2^2 + 3^2) = √13. Therefore, the magnitude of −4⇀

is 4√13. This means that statement B is true.

- The direction of −4⇀

is opposite to the direction of ⇀

because the scalar –4 is negative. This means that statement C is false.

- The vector −4⇀

is in the third quadrant because its components are both negative. This means that statement D is false.

- The direction of −4⇀

is 180° greater than the inverse tangent of its components because it is opposite to ⇀

. The inverse tangent of its components is tan^(-1)(–12/–8) = tan^(-1)(3/2). Therefore, the direction of −4⇀

is 180° + tan^(-1)(3/2). This means that statement E is true.

Therefore, the correct statements are A, B, and E.

The x- and y-intercept values in the graph for the function f and in the table for the function g(x), indicates that the correct option is option C

The x-intercept is the point at which the y-value is 0, and the coordinates of the point is specified as the x-intercept.

The x-intercept is the point at which the x-value is 0, and the coordinates of the point is specified as the y-intercept

The question compares the x- and y-intercepts of the graph and the function in the table

The x-intercept of the function f in the graph are; (0, 3)

The y-intercept of the function f in the graph are; (4, 0)

The function g(x) in the table indicates that the x- and y-intercepts are;

The value of g(x) is 0 at the ordered pair (1, 0), therefore, the x-intercept of g(x) is (1, 0)

The value of x is 0 at the ordered pair (0, 4), therefore, the function, g(x) has a y-intercept at the point (0, 4)

Therefore, the function f and g have different intercepts, but the value in the table and the graph indicates that as x approaches infinity, the y-value, approaches -1, the correct option is therefore, option C

Learn more on the x- and y-intercept of a graph here: https://brainly.com/question/29252186

#SPJ1

Answer:

The first one

Step-by-step explanation:

She cant buy anything over $15, but she can buy something thats $15 :))

The length of e is 29.53 inches.

In the following, the law of sine is presented in detail: In a triangle, the sine of angle A divided by side "a" equals the sine of angle B divided by side "b" equals the sine of angle C divided by side "c".

Given:

f= 33 inches

<F= 140, <D = 5

Now,

<E= 180 - (<F+ <D) = 180 - (140 + 5) = 35

Using Sine law

sin F / f = sin E/ e

sin 140 / 33 = sin 35 / e

0.642/ 33 = 0.573 / e

0.0194 e= 0.573

e= 29.53 inches

Hence, the length of e is 29.53 inches.

Learn more about sine law here:

https://brainly.com/question/17289163

#SPJ1

According to the given values in the question:

The Amortization period is:

= \(8 \ years\times 12 \ months\)

= \(96 \ months\)

Number of months of Amortization is:

= \(3 \ months \ in \ 2020+(4 \ years\times 12 \ months)\)

= \(3+48\)

= \(51 \ months\)

Now,

On bonds payable, the premium will be:

= \(Issue \ price - Face \ value\)

= \((100000\times 103 \ percent)- 100000\)

= \(103000-100000\)

= \(3000\) ($)

The Unamortized premium will be:

= \(Premium - Unamortized \ premium\)

= \(3000-(3000\times \frac{51}{96} )\)

= \(3000-1593.75\)

= \(1406.25\) ($)

hence,

The carrying value as of December  31, 2024 will be:

= \(100000+1406.25\)

= \(101406.25\) ($)

Learn more about the bond carrying value here:

https://brainly.com/question/20630991

Answer:

Step-by-step explanation:

X = # of years

8% of 1100 = 88

88X =2000

X = 22.7

23 years

Type I error is "Megan's results show significant improvements in health associated with a whole foods diet."

A Type I error occurs when the null hypothesis is rejected, even though it is true.

In this case, the null hypothesis states that a whole foods diet would not have any impact on general health.

Therefore, a Type I error would occur if Megan's results show significant improvements in health associated with a whole foods diet.

This means that Megan would reject the null hypothesis and conclude that a whole foods diet does have an impact on general health, even though it is not true.

So, the statement that would indicate a Type I error is "Megan's results show significant improvements in health associated with a whole foods diet."

To learn more on Null hypothesis click:

https://brainly.com/question/30821298

#SPJ1

Answer:

D

Step-by-step explanation:

A triangle with sides 2, 4.5, and 6 is similar to a triangle with sides 4, 9, and 12.

\( \frac{4}{2} = \frac{9}{4.5} = \frac{12}{6} = 2\)

Answer:

Median ( Q2) = 6

Q1 ( lower quartile) = 4.5

Q3 ( upper quaartile) = 10.5

Step-by-step explanation:

3,4,4,5,5,6,  6,6  ,6,7,9,12,14,15

6,6 is the median but we only need I median. So 6 + 6 = 12, 12 divided 2 = 6.

3,4,4,5,5,6,  is the Q1 ( lower quartile ) and median of Q1, is 4,5. 4 + 5 = 9. 9 divided 2 = 4.5

6,7,9,12,14,15  is Q3 ( upper quartile) 9,12 is median but we only need one. So 9 + 12 =21. 21 divided 2 = 10.5

The correct answer is C. It is the graph of f(x) translated 11 units to the left.

The correct answer is:

C. It is the graph of f(x) translated 11 units to the left.

When we have a function of the form g(x) = f(x - a), it represents a horizontal translation of the graph of f(x) by 'a' units to the right if 'a' is positive and to the left if 'a' is negative.

In this case, g(x) = f(x - 11), which means that the graph of f(x) is being translated 11 units to the right. However, the answer options do not include this specific transformation. The closest option is option C, which states that the graph of g(x) is translated 11 units to the left.

The graph of f(x) = x is a straight line passing through the origin with a slope of 1. If we apply the transformation g(x) = f(x - 11), it means that we are shifting the graph of f(x) 11 units to the right. This results in a new function g(x) that has the same shape and slope as f(x), but is shifted to the right by 11 units.

Therefore, the correct answer is C. It is the graph of f(x) translated 11 units to the left.

for more such question on graph visit

https://brainly.com/question/19040584

#SPJ8

Step-by-step explanation:

\( {x}^{2} + 8x + 7 \\ \)

Answer:

£1.44

Step-by-step explanation:

N1 = £0.12

N12 = 12 × N1 = 12 × £0.12 = £1.44

The Code of Conduct is a moral guide for military members when isolated or held against their will by entities hostile to the U.S.

A code of conduct is a set of laid down rules that sets the standard for behavior under specific circumstances.

Hence, the Code of Conduct is a moral guide for military members when isolated or held against their will by entities hostile to the U.S.

Missing parts;

The Code of Conduct is a ____________ for military members when isolated or held against their will by entities hostile to the U.S. moral guide recommended procedure mandatory directive direct order

Learn more about code of conduct:https://brainly.com/question/12990307

#SPJ1

Therefore , the solution of the given problem of interest comes out to be

$4,962.93 money more made by Alexander.

Simple interest is calculated by dividing the principal by the borrowing cost, the remaining time, and other elements. The simple return formula in marketing is principal + interest plus hours. Utilizing this method is the simplest way to calculate interest. As a percentage of the principle sum is the most frequent way to calculate income. For instance, he will only pay his portion of the 100% cost if he borrows $100 from a friend and agrees to pay the loan back with 5% interest.. You have to pay interest on money you borrow, and you have to charge interest on money you lend.

Here,

Given :

Luke :

Principal amount = $86,000

and rate of interest =  5 ⅛ % or 41/8% or 5.125%

Alexander :

Principal amount = $86,000

rate of interest = 5 ⅝ % or 45/8% or 5.625%

To find the amount of money after time =8 years.

So ,

using compound formula :

=> A = P\((1 + r/n)^{nt}\)

For luke = P=86000\((1 + 41/8*1)^{1*8}\) = $42,276.33

For  Alexander =   P=86000\((1 + 45/8*1)^{1*8}\) = $47,239.26

The amount made by Alexander by luke

=> 47,239.26 - 42,276.33 = 4,962.93

Therefore , the solution of the given problem of interest comes out to be

$4,962.93 money more made by Alexander.

To know more about interest visit:

https://brainly.com/question/28792777

#SPJ1

Answer:

x3−12x2+38x−17x−7=x2−5x+3+4x−7           Brainliest pls???

Step-by-step explanation:

Write the problem in the special format:

x−7  

x3 −12x2 +38x −17

Step 1

Divide the leading term of the dividend by the leading term of the divisor:

x3

x

=x2.

Write down the calculated result in the upper part of the table.

Multiply it by the divisor: x2(x−7)=x3−7x2.

Subtract the dividend from the obtained result: (x3−12x2+38x−17)−(x3−7x2)=−5x2+38x−17.

x2  

x−7  

x3 −12x2 +38x −17

x3

x

=x2

−  

x3 −7x2

−5x2 +38x −17

x2(x−7)=x3−7x2

Step 2

Divide the leading term of the obtained remainder by the leading term of the divisor:

−5x2

x

=−5x.

Write down the calculated result in the upper part of the table.

Multiply it by the divisor: −5x(x−7)=−5x2+35x.

Subtract the remainder from the obtained result: (−5x2+38x−17)−(−5x2+35x)=3x−17.

x2 −5x  

x−7  

x3 −12x2 +38x −17

−  

x3 −7x2

−5x2 +38x −17

−  

−5x2 +35x

3x −17

−5x2

x

=−5x

−5x(x−7)=−5x2+35x

Step 3

Divide the leading term of the obtained remainder by the leading term of the divisor:

3x

x

=3.

Write down the calculated result in the upper part of the table.

Multiply it by the divisor: 3(x−7)=3x−21.

Subtract the remainder from the obtained result: (3x−17)−(3x−21)=4.

x2 −5x +3

x−7  

x3 −12x2 +38x −17

−  

x3 −7x2

−5x2 +38x −17

−  

−5x2 +35x

3x −17

−

3x −21

4

3x

x

=3

3(x−7)=3x−21

Since the degree of the remainder is less than the degree of the divisor, then we are done.

The resulting table is shown once more:

x2 −5x +3

 Hints

x−7  

x3 −12x2 +38x −17

x3

x

=x2

−  

x3 −7x2

−5x2 +38x −17

−  

−5x2 +35x

3x −17

−

3x −21

4

x2(x−7)=x3−7x2

−5x2

x

=−5x

−5x(x−7)=−5x2+35x

3x

x

=3

3(x−7)=3x−21

Therefore,

x3−12x2+38x−17

x−7

=x2−5x+3+

4

x−7

Answer:

x3−12x2+38x−17

x−7

=x2−5x+3+

4

x−7

Answer:

(-7/2, 3/2)

Step-by-step explanation:

picture below ;)

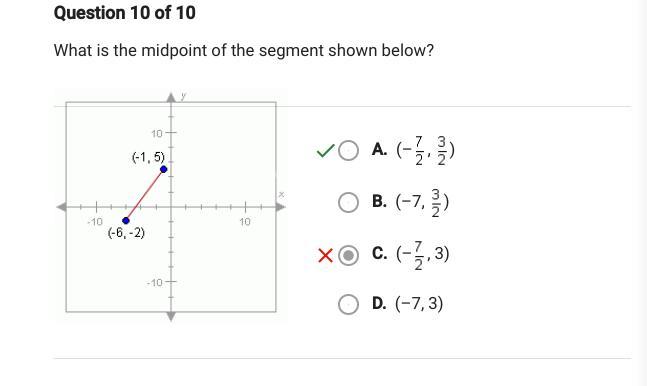
A line became by joining two coordinates, the midpoint of the given line segment is (-3.5,1.5).

A line segment is become by joining two points which has specific coordinates.

To find the midpoint coordinate between any two points then we have to add the x's coordinates and divide by two and similarly y's coordinates and divide by two.

For example, if you have two points as (a,b) and (c,d) then the coordinate of the midpoint joining this line will be (  \(\frac{a+c}{2}\), \(\frac{b+d}{2}\) ).

Since the points are  (-1,5) (-6,-2) so the midpoint joining this line segment will be

( \(\frac{-6-1}{2}\), \(\frac{5-2}{2}\) ) so (-3.5,1.5) will be the midpoint of the line segment.

For more information about line segment

https://brainly.com/question/25727583

#SPJ5

Let us first find the graph of the line of best fit using the given data.

Input the data into Desmos or any other graphing calculator

The graph of the line of best fit is shown below

As you can see from the above graph, the point (-2, 2) is not on the line of best fit, it is not very near the line of best fit but rather far away from it, it is not above the line of best fit but rather it is below the line of best fit.

Therefore, the correct statement is option D.

D. It is quite a bit below the line

Answerurdsrd d e

Step-by-step explanation:

The two values of y such that the barn is 50 yards from the well

The length of line in an ordered pair is calculated using the formula

d = √{(x₂ - x₁)² + (y₂ - y₁)²}

where

d = distance between the points

x₂ and x₁ = points in x coordinates

y₂ and y₁ = points in y coordinates

distance between points  (-1, 1) and (-1,, y) is calculated to be 50 yards and hence we solve for y

d = √{(x₂ - x₁)² + (y₂ - y₁)²}

50 =√{(-1 - -1)² + (1 - y)²}

50 =√{ (1 - y)²}

2500 = (1 - y) (1 - y)

2500 = 1 - 2y + y²

y² - 2y - 2499 = 0

solving the quadratic equation gives

y = 51 OR -49

Learn more about length of line segment here:

https://brainly.com/question/29706244

#SPJ1

The needed number of days at 10 degrees is given as follows:

11 days.

The slope-intercept equation for a linear function is presented as follows:

y = mx + b

In which:

For this problem, we have that when x decreases by 5, y increases by 2, hence the slope m is given as follows:

m = -2/5

m = -0.4.

Hence the time needed for a temperature of 10 degrees is given as follows:

9 + 2 = 11 days.

More can be learned about linear functions at https://brainly.com/question/15602982

#SPJ1