The sum of two times x and 3 times y is 5. The difference of x and y is 5. Write two equations and graph to find the value of y.
Answers
Answer:
x = 4 and y = -1
Step-by-step explanation:
Related Questions
write an algebraic equation for the followingn problem and then solve for it. Hilltop dormitory just purchased a new soft drink machine on sale for $480. The sale price was 75% of the original price. What was the original price of the soft drink machine?
Answers
Answer:
Step-by-step explanation:480 x o.75=360
and now you add this amount on payed
360 + 480=840 was original price
What is the y-intercept of the graph of the function f(x) = x2 + 3x + 5?
0 (0,-5)
0 (0, -3)
O (0,3)
0 (0,5)
Answers
Answer:
(0,5)
Step-by-step explanation:
f(x) = x^2 + 3x + 5
The y intercept is when x =0
f(0) = 0 + 3*0 + 5
f(0) = 5
(0,5)
Lisa randomly selected 30 adult dogs from two different breeds. She gathered data about their weights and created the dot plots
shown.
Select the true statement.
Breed A
24
Breed B
24
26
26
28
28
30 32
Weight (pounds)
34
po 32
Weight (pounds)
34
36
36
30
●
38
40
40
A.
Dogs of breed B typically weigh more than dogs of breed A
B.
Dogs of breed A and breed B typically weigh the same.
C. There is too much overlap to make a generalization comparing the weights of dogs of breed A and breed B.
D. Dogs of breed A typically weigh more than dogs of breed B.
Answers
The true statement is Statement A which is dogs of breed B typically weigh more than dogs of breed A using histogram in probability concept.
What is a histogram in probability?The likelihood of each possible occurrence is displayed on the y-axis of a probability histogram. A histogram is a statistical data display that makes use of rectangles to illustrate the frequency of data items in successive numerical intervals of equal size. The dependent variable is plotted along the vertical axis in the most typical type of histogram, while the independent variable is plotted along the horizontal axis. The distribution of data is depicted graphically in a histogram. A collection of neighboring rectangles, each with a bar that represents a certain type of data, is used to illustrate a histogram. Fill L1 with the values of the random variable (remember to use the class midpoints for continuous random variables). The associated percentages should be entered into L2 with a decimal format.
To know more about histograms in probability, visit:
https://brainly.com/question/16819077
#SPJ9
3. Observe this Input/Output table. Which rule describes the function? Please help

Answers
Answer: n^2
Step-by-step explanation:
The output for each input matches the function.
3²=9
5²=25
7²=49
wwhat is 21654731642137 x 726323327 +.00001238123-.8237102837 x 1999
Answers
Answer:
1.57283367316E22 ooooooooooooooo
Answer:
1.57283 × 10^{22}
Step-by-step explanation:
Multiply the numbers first, then calculate the difference.
Find the probability that a randomly selected point within the square falls in the red-shaded triangle. 3 3 4 P = [?] 4
Answers
The required probability is 3 √7 / 32.
Given, a square with sides of length 4 units and a red-shaded triangle with sides 3 units, 3 units and 4 units. We need to find the probability that a randomly selected point within the square falls in the red-shaded triangle.To find the probability, we need to divide the area of the red-shaded triangle by the area of the square. So, Area of square = 4 × 4 = 16 square units. Area of triangle = 1/2 × base × height.
Using Pythagorean theorem, the height of the triangle is found as: h = √(4² − 3²) = √7
The area of the triangle is: A = 1/2 × base × height= 1/2 × 3 × √7= 3/2 √7 square units. So, the probability that a randomly selected point within the square falls in the red-shaded triangle is: P = Area of triangle/Area of square= (3/2 √7) / 16= 3 √7 / 32.
for such more questions on probability
https://brainly.com/question/29070527
#SPJ8
What expression represents all solutions to cos(x)=0.15
Answers
Answer:
it od domedfg
Step-by-step explanation:
hihihi
what is the simplest from of the ratio 40:16 ?
Answers
Answer:
5 : 2
Step-by-step explanation:
40:16
Divide each side by 8
40/8:16/8
5 : 2
Answer:
5 :2
Step-by-step explanation:
40 : 16
= 40/16
= 4*10 / 4*4
= 10/4
= 5*2 / 2*2
=5/2
FIND EACH LENGHT BELOW ITS AN ALEX ASSIGNMENT UNDER THE CATEGORY SEGMENTS IN CIRCLES

Answers
The length in each circle is:
(a) CD = 19.5 units
(b) UZ = 12.8 units
How to find the length in each circle?(a) The Intersecting Secant-Tangent Theorem states that "if two secant lines intersect outside a circle, and a tangent line is drawn from the point of intersection to the circle, then the product of the lengths of the two secant segments is equal to the square of the length of the tangent segment".
Using the theorem, we have:
EC * ED = EG²
6.5 * ED = 13²
6.5ED = 169
ED = 169/6.5
ED = 26 units
ED = EC + CD
26 = 6.5 + CD
CD = 26 - 6.5
CD = 19.5 units
(b) The Secant-Secant Theorem states that "if two secant segments which share an endpoint outside of the circle, the product of one secant segment and its external segment is equal to the product of the other secant segment and its external segment".
Using the theorem above, we can say:
UZ * UW = UX * UY
UZ * 40 = 8 * 64
40UZ = 512
UZ = 512/40
UZ = 12.8 units
Learn more about Intersecting Secant-Tangent Theorem on:
brainly.com/question/27160891
#SPJ1
4 Write the following numbers in order from greatest to least. Student Distance Walked to School Christian 0.49 of a mile Athena 78% of a mile Lakyn of a mile Alexis of a mile Christian. Athera. Lokyn, Alexis O Athera, Christian, Alexis, Lokyn Athera. Christian. Lokyn. Alexis a Lokyn. Alexis, Christian, Athera
Answers
We have 4 numbers and we have to sort them from greatest to least.
\(\begin{gathered} 0.49 \\ 78\%=0.78 \\ \frac{3}{7}=0.\bar{428571}\text{ (periodic)} \\ \frac{7}{15}=0.4\bar{6} \end{gathered}\)If we ordered them we have: 0.78, 0.49, 0.46..., 0.428471...
This corresponds to Athena, Christian, Alexis, Lokyn.
Other way to solve it would have been to look for the common denominator for all this numbers, and then compare the numerators.
can you solve this question?

Answers
By the Mean Value Theorem, there exists a number c in (1, 7) such that ƒ'(c) = 2/c and 2/c = ln7 / 6, and c ≈ 0.909.
How to calculate the valueThe Mean Value Theorem (MVT) states that if a function ƒ(x) is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), then there exists a number c in (a, b) such that:
ƒ'(c) = [ ƒ(b) - ƒ(a) ] / (b - a)
ƒ(x) = 2lnx - 8 is continuous on the closed interval [1, 7], since it is the sum and composition of continuous functions.
ƒ(x) = 2lnx - 8 is differentiable on the open interval (1, 7), since its derivative ƒ'(x) = 2/x is defined and continuous on (1, 7).
Therefore, the Mean Value Theorem can be applied to ƒ(x) on [1, 7]. To find the value of c, we need to solve the equation:
ƒ'(c) = [ ƒ(b) - ƒ(a) ] / (b - a)
Substituting the given values, we get:
2/c = [ 2ln7 - 2ln1 ] / (7 - 1)
2/c = ln7
c = 2 / ln7
c ≈ 0.909
Therefore, by the Mean Value Theorem, there exists a number c in (1, 7) such that ƒ'(c) = 2/c and 2/c = ln7 / 6, and c ≈ 0.909.
Learn more about mean on:
https://brainly.com/question/1136789
#SPJ1
Katarina bought a package of 500 stickers. 25% of the stickers are hearts. The remaining stickers
are stars. Select 2 statements that are true.
A.Katarina has 100 heart stickers.
B.Katarina has 375 star stickers.
C.The package contains 20 sheets of stickers
3
D.75% of the stickers are stars.
E.The number of heart stickers is the same as the number of star stickers
Answers
25% of 500 is 125, 500-125 is 375 which is how many remaining star stickers there are.
The correct statement are;
B. Katarina has 375 star stickers.
D. 75% of the stickers are stars.
What is mean by Percentage?A number or ratio that can be expressed as a fraction of 100 or a relative value indicating hundredth part of any quantity is called percentage.
Given that;
Katarina bought a package of 500 stickers. 25% of the stickers are hearts. The remaining stickers are stars.
Now,
Since, Katarina bought a package of 500 stickers. 25% of the stickers are hearts. The remaining stickers are stars.
Hence, The number of hearts = 25% of 500
= 25/100 × 500
= 25 × 5
= 125
And, Number of stars = 500 - 125
= 375
= 75% of 500
Thus, The correct statement are;
B. Katarina has 375 star stickers.
D. 75% of the stickers are stars.
Learn more about the percent visit:
https://brainly.com/question/24877689
#SPJ2
A snake tank measures 1.8 m x 0.5 m x 0.5 m. What is the surface area of the tank including the top? Use the formula: SA = 2hl+2hw+2lw
Answers
Answer:
4.1
Step-by-step explanation:
1.8 x 0.5 = 0.9
0.5 x 0.5 = 0.25
2(0.9 + 0.9 + 0.25) = 2(1.8 + 0.25) = 2(2.05)
2 x 2.05 = 4.1
Therefore the answer is 4.1
I hope that was helpful!
Rewrite quotient log 29
Answers
The quotient log 29 can be rewritten as 1 + log 2.9.
The quotient of two numbers is the result of dividing one number by another. In mathematics, the logarithm is the inverse operation to exponentiation, just as division is the inverse of multiplication.
A logarithm is the exponent that a fixed base must be raised to produce a given number. The notation logx (read "log base x") denotes the logarithm of a number with respect to a base x.
Hence, when we say the quotient log 29, it implies that we need to determine the logarithm of 29, which we can represent as log 29, as there is no base specified. In general, we assume the base to be 10.
Now, we have:
`log 29`
To rewrite this quotient, we can consider the following steps:
Step 1: Break the number down into factors
29 is a prime number; it is not divisible by any other number except for 1 and itself. Therefore, we cannot break it down into factors.
Step 2: Find the prime factorization of the divisor
Since the divisor is not provided, we cannot perform this step.
Step 3: Apply the quotient rule of logarithms
The quotient rule of logarithms states that:
log (a / b) = log a - log b
We can use this rule to rewrite `log 29` as follows:
`log 29 = log (10 * 2.9)`
`log 29 = log 10 + log 2.9`
`log 29 = 1 + log 2.9`
To learn more about : quotient
https://brainly.com/question/11418015
#SPJ8
Which of these best explains the next step to simplify this expression?

Answers
Answer:
Make the -4 exponent in the denominator positive.
Approximate 1.50659165 to the nearest thousandth
Answers
Explanation
Given
\(1.50659165\)We can approximate to the nearest thousandth by rounding the number to 3 places after the decimal point.
Answer:
\(1.507\)I need help with this!

Answers
The length AC in the kite is 8.7 cm.
How to find the side AC in the kite?A kite is a quadrilateral that has two pairs of consecutive equal sides and
perpendicular diagonals. Therefore, let's find the length AC in the kite.
Hence, using Pythagoras's theorem, let's find CE.
Therefore,
7² - 4² = CE²
CE = √49 - 16
CE = √33
CE = √33
Let's find AE as follows:
5²- 4² = AE²
AE = √25 - 16
AE = √9
AE = 3 units
Therefore,
AC = √33 + 3
AC = 5.74456264654 + 3
AC = 8.74456264654
AC = 8.7 units
learn more on kite here: https://brainly.com/question/27975644
#SPJ9
Simplify the expression StartFraction a b Superscript 3 Baseline over a Superscript 4 Baseline b EndFraction plus left-parenthesis c Superscript 2 Baseline right-parenthesis Superscript 3 Baseline
Answers
The simplification of the expression ab³/a⁴b + (c²)³ is determined as b²/a³ + c⁶.
What is the simplification of the expression?The given expression is simplified as follows;
The given expression is written as;
ab³/a⁴b + (c²)³
To simplify the expression given above, we will divide the fraction with the common factor as follows;
From the numerator; ab³, we will factor out "ab"
From denominator; a⁴b, we will factor out "ab"
The resulting expression becomes;
ab³/a⁴b + (c²)³
= b²/a³ + c⁶
Note: for the power of c, we simplify by multiplying 2 and 3 = 6
Thus, the simplification of the expression ab³/a⁴b + (c²)³ is determined as b²/a³ + c⁶.
Learn more about simplification here: https://brainly.com/question/28008382
#SPJ1
A bucket contains six white balls and five red balls. A sample of four balls is selected
at random from the bucket, without replacement. What is the probability that the
sample contains...
Exactly two white balls and two red balls?
At least two white balls?
Answers
To solve this problem, we can use the formula for probability:
P(event) = number of favorable outcomes / total number of outcomes
First, let's find the total number of outcomes. We are selecting 4 balls from 11 without replacement, so the total number of outcomes is:
11C4 = (11!)/(4!(11-4)!) = 330
where nCr is the number of combinations of n things taken r at a time.
Now let's find the number of favorable outcomes for each part of the problem.
Part 1: Exactly two white balls and two red balls
To find the number of favorable outcomes for this part, we need to select 2 white balls out of 6 and 2 red balls out of 5. The number of ways to do this is:
6C2 * 5C2 = (6!)/(2!(6-2)!) * (5!)/(2!(5-2)!) = 15 * 10 = 150
So the probability of selecting exactly two white balls and two red balls is:
P(2W2R) = 150/330 = 0.45 (rounded to two decimal places)
Part 2: At least two white balls
To find the number of favorable outcomes for this part, we need to consider two cases: selecting 2 white balls and 2 red balls, or selecting 3 white balls and 1 red ball.
The number of ways to select 2 white balls and 2 red balls is the same as the number of favorable outcomes for Part 1, which is 150.
To find the number of ways to select 3 white balls and 1 red ball, we need to select 3 white balls out of 6 and 1 red ball out of 5. The number of ways to do this is:
6C3 * 5C1 = (6!)/(3!(6-3)!) * (5!)/(1!(5-1)!) = 20 * 5 = 100
So the total number of favorable outcomes for selecting at least two white balls is:
150 + 100 = 250
And the probability of selecting at least two white balls is:
P(at least 2W) = 250/330 = 0.76 (rounded to two decimal places)
The sample mean for the confidence interval 56 < μ < 62 is
Answers
Answer:
The sample mean is 59
Step-by-step explanation:
From the confidence interval given above, it can be said that the sample mean is between a lower limit of 56 and an upper limit of 62
Margin of Error (E) = (upper limit - lower limit) ÷ 2 = (62 - 56) ÷ 2 = 6 ÷ 2 = 3
Sample mean = lower limit + E = 56 + 3 = 59
Please help. The question is in the attached image

Answers
∠G+∠H+∠J=180 and ∠K+∠L+∠M=180 from the angle sum property of triangle, ∠H=∠L (3rd Angle Theorem) and ∆GHJ≅∆KLM from ASA congruency theorem.
In the given question we have to prove ∆GHJ congrurnce ∆KLM.
Given that: ∠G≅∠K, ∠J≅∠M, \(\over{HJ}\) ≅ \(\over{LM}\).
As given that;
∠G≅∠K
∠J≅∠M
\(\over{HJ}\) ≅ \(\over{LM}\)
So from the angle sum property of triangle
∠G+∠H+∠J=180................(1)
∠K+∠L+∠M=180.................(2)
Now equation equation 1 and 2
∠G+∠H+∠J=∠K+∠L+∠M
As we know that ∠G=∠K, ∠J=∠M
So now the expression is
∠G+∠H+∠J=∠G+∠L+∠J
After solving ∠H=∠L (3rd Angle Theorem)
Since, ∠H=∠L, HJ=LM and ∠G=∠K, so from the theorem Angle Side Angle(ASA) congruency,
∆GHJ≅∆KLM
To learn more about ASA congruency theorem link is here
brainly.com/question/1593616
#SPJ1
What does the net decimal equivalent (NDE) represent?
Answers
Answer:
the product of the decimal equivalents of all discount in the series
The points A, B, C and D lie in order on a straight line
such that
AB:BD = 1:2
AC:CD= 7:2
Find AB:BC:CD

Answers
Answer:
7 + 2 = 9, so AC = 7/9 and CD = 2/9
1 + 2 = 3, so AB = 1/3 = 3/9 and
BD = 2/3 = 6/9
AB + BC = AC
3/9 + BC = 7/9, so BC = 4/9
AB:BC:CD = (3/9):(4/9):(2/9) = 3:4:2
During halftime of a football game, a sling shot launches T-shirts at the crowd A T-shirt is launched from a height of 6 feet with an initial upward velocity of 72 feet per second Use the
equation h(t) = -16 +72t+6, where t is time in seconds and h(t) is height. How long will it take the T-shirt to reach its maximum height? What is the maximum height?
Answers
Answer:
Hope this helps ;)
Step-by-step explanation:
To find the time it takes the T-shirt to reach its maximum height, we need to find the value of t when the velocity of the T-shirt is zero, because at this point the T-shirt has reached its maximum height and starts falling back down. We can find the velocity of the T-shirt by taking the derivative of the height equation with respect to time:
v(t) = h'(t) = 72
The velocity of the T-shirt is a constant 72 feet per second, so it will never reach a velocity of zero and will never reach its maximum height. The T-shirt will keep going up indefinitely.
If the problem had specified that the T-shirt was launched with an initial upward velocity of -72 feet per second (meaning it was launched downward), then we could have found the time it takes the T-shirt to reach its maximum height by setting v(t) = 0 and solving for t. In this case, we would find that t = 1, so it would take the T-shirt 1 second to reach its maximum height. The maximum height would be h(1) = -16 + 72(1) + 6 = 62 feet.
Solve for X. Write down what type of solution the equation has.1) -48 (X-24) + 12 (X + 4) = X + 15 2) 12 (X + 2) - 4x = 4 (2X + 11 ) -20
Answers
Use the properties of the real numbers to simplify each side of each equation. Then, use the properties of equalities to solve for x.
1)
\(-48(x-24)+12(x+4)=x+15\)Use the distributive property to expand each parenthesis on the left hand side of the equation:
\(\begin{gathered} \Rightarrow-48(x)-48(-24)+12(x+4)=x+15 \\ \Rightarrow-48(x)-48(-24)+12(x)+12(4)=x+15 \end{gathered}\)Simplify each term by multiplying the coefficients times the expressions inside the parenthesis:
\(\begin{gathered} \Rightarrow-48x-48(-24)+12(x)+12(4)=x+15 \\ \Rightarrow-48x+1152+12(x)+12(4)=x+15 \\ \Rightarrow-48x+1152+12x+12(4)=x+15 \\ \Rightarrow-48x+1152+12x+48=x+15 \end{gathered}\)Use the commutative property to change the order of the terms on the left hand side of the equation to bring like terms together. Then, add them:
\(\begin{gathered} \Rightarrow-48x+12x+1152+48=x+15 \\ \Rightarrow-36x+1152+48=x+15 \\ \Rightarrow-36x+1200=x+15 \end{gathered}\)Substract x from each side of the equation:
\(\begin{gathered} \Rightarrow-36x+1200-x=x+15-x \\ \Rightarrow-37x+1200=15 \end{gathered}\)Substract 1200 from each side of the equation:
\(\begin{gathered} \Rightarrow-37x+1200-1200=15-1200 \\ \Rightarrow-37x=-1185 \end{gathered}\)Divide both sides by -37:
\(\begin{gathered} \Rightarrow-\frac{37x}{-37}=-\frac{1185}{-37} \\ \Rightarrow x=\frac{1185}{37} \end{gathered}\)Since 1185/37 is a rational number, then this equation has a rational solution.
2)
\(12(x+2)-4x=4(2x+11)-20\)
Use the distributive property to expand the parenthesis on each side of the equation, and simplify the resulting expressions:
\(\begin{gathered} \Rightarrow12(x)+12(2)-4x=4(2x)+4(11)-20 \\ \Rightarrow12x+24-4x=8x+44-20 \\ \Rightarrow8x+24=8x+24 \end{gathered}\)Since the expression 8x+24=8x+24 is an identity (the coefficients and constant terms are the same on both sides), then any number is a solution for this equation on the variable x.
Therefore, this equations has infinitely many solutions.
if y= x+3/6-x, what is the value of y when x =7i?
Answers
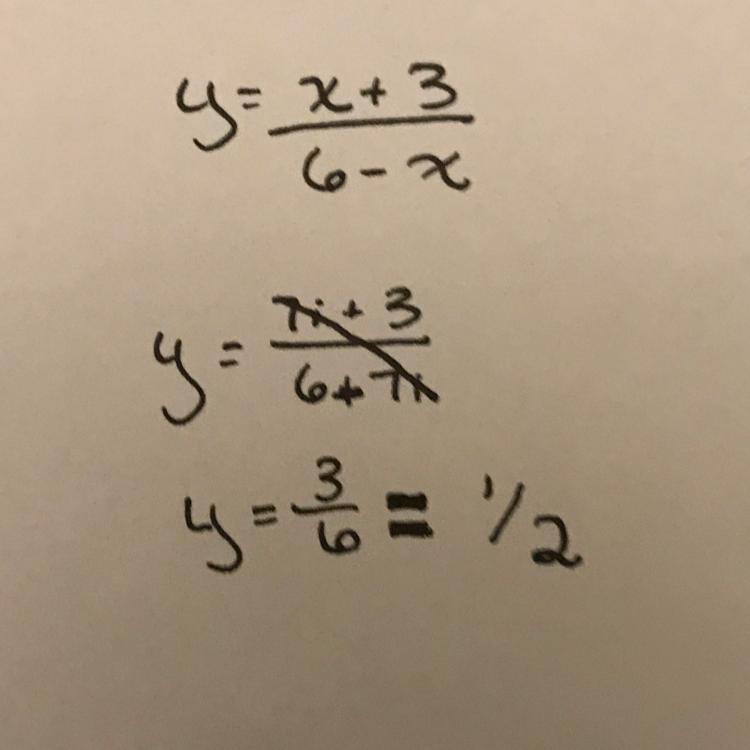
A side of the triangle below has been extended to form an exterior angle of 74°. Find the value of x.

Answers
Answer:
Step-by-step explanation:
The adjacent angle to the missing angle must sum to 180 degrees. So a=180-74=106 degrees. The sum of the three angles of the triangle must also sum to 180.
x+49+106=180
x+155=180
x=25
Answer:
106
Step-by-step explanation:
x+49=74
x=74-49=25
y=74=180
y=180-74=106
im sorry im late if u see this yw!
Pam kicked a soccer ball down the field. Part of the ball's path, including its highest
point, is described by the function below, where f(x) is the height of the ball in feet.
According to the function, what is the ball's maximum height, in feet? (Use only the
digits 0-9 to enter the height.)
f(x) =
12x2+2x
Answers
Answer:
maximum height is 45/4 in feet
The maximum height of the ball is 45/4 in feet
What is the unitary method?The unitary method is a method for solving a problem by the first value of a single unit and then finding the value by multiplying the single value.
Given tha Pam kicked a soccer ball down the field. Part of the ball's path, including its highest point, is described by the function below, where f(x) is the height of the ball in feet.
F(x)= 12x^2+2x
Thus for this quadratic , the max value will occur at x= -b/2a
= - 2 / (2 x 1/12) = -12
Plug in -12 to find the max height
= (-12)^2 + 2 x-12
= 45/4 in feet
Learn more about the unitary method, please visit the link given below;
https://brainly.com/question/23423168
#SPJ2
i need help on this stuck on it

Answers
Answer:
5=148 and 8=32
Step-by-step explanation:
For this equation we know since the lines are parelle that they will produce the same angle degrees.
so 2,4,6,and 8 are all 32
if we subtract 180 (the dregree of a stright line) from 32 we get 148
so 148 is for 1,3,5, and 7
Suppose we modeled the world population in the second half of the 20th century by the equation
P(t)=2560e0.017185t. Use this equation to estimate the average world population during the time period of 1950 to 2000. (Round your answer to the nearest million.)
Answers
The average world population during the time period of 1950 to 2000 is approximately 4.7 billion.
To estimate the average world population, we need to evaluate the population at both endpoints and then take the average.
Substituting t = 0 (which corresponds to the year 1950) into the equation, we get:
P(0) = 2560e^(0.017185*0) = 2560
So the estimated world population in 1950 was 2560 million.
Substituting t = 50 (which corresponds to the year 2000) we get:
P(50) = 2560e^(0.017185*50) = 6789.9...
Rounding to the nearest million, we get P(50) ≈ 6790 million.
The average world population during the time period of 1950 to 2000 is approximately (2560+6790)/2 = 4675 million, or 4.7 billion (rounded to the nearest billion).
To know more about Average:
https://brainly.com/question/2906096
#SPJ4