The sides of the base of this square right prism are 16 centimeters each and the height of the prism is 10 centimeters. What is the surface area of the prism?
a)964 cm^2
b)1000 cm^2
c)1152 cm^2
d)1232 cm^2
Answers
The surface area of a prism is calculated by adding the areas of all of its faces. In this square right prism, there are two congruent rectangular faces with an area of 16 x 10 = 160 cm^2 each, and four congruent square faces with an area of 16 x 16 = 256 cm^2 each. Thus, the total surface area of the prism can be calculated by adding the areas of all the faces, which is 2 x 160 cm^2 + 4 x 256 cm^2 = 1152 cm^2.
Therefore, the correct answer is c) 1152 cm^2. It is important to remember the formula for the surface area of a prism and to carefully calculate the area of each face before adding them together.
To learn more about prism click here : brainly.com/question/12649592
#SPJ11
Related Questions
Jeffrey has already run 3/8 of the race. What fraction of the race does Jeffrey have left?
Answers
Answer:
5/8
Step-by-step explanation:
1 whole race (8/8) - 3/8 = 5/8
consider the sample data (1, 1),(3, 2),(2, 4). find the equation of the regression line for these sample data.
Answers
The equation of the regression line for the sample data (1, 1), (3, 2), (2, 4) is y = (1/2) × x + 4/3.
To find the equation of the regression line for the given sample data, we can use the method of linear regression.
The regression line represents the best-fitting line that minimizes the sum of the squared differences between the observed data points and the predicted values on the line.
Let's denote the independent variable as x and the dependent variable as y.
We have three data points: (1, 1), (3, 2), and (2, 4).
Calculate the mean of x and y:
Mean of x (\($\bar{x}$\)) = (1 + 3 + 2) / 3 = 2
Mean of y (\($\bar{y}$\)) = (1 + 2 + 4) / 3 = 7/3
Calculate the deviations from the means for x and y:
Deviations from the mean of x (x - \($\bar{x}$\)): (-1, 1, 0)
Deviations from the mean of y (y - \($\bar{y}$\)): (-4/3, -1/3, 5/3)
Calculate the product of the deviations for x and y:
Product of deviations (x - \($\bar{x}$\))(y - \($\bar{y}$\)): (4/3, -1/3, 0)
Calculate the sum of the product of deviations:
Sum of (x - \($\bar{x}$\))(y - \($\bar{y}$\)) = (4/3) + (-1/3) + 0 = 1
Calculate the squared deviations for x:
Squared deviations for x \((x - \bar{x} )^2\): (1, 1, 0)
Calculate the sum of the squared deviations for x:
Sum of \((x - \bar{x} )^2\) = 2
Calculate the slope of the regression line (b):
b = sum of (x - \($\bar{x}$\))(y - \($\bar{y}$\)) / sum of \((x - \bar{x} )^2\) = 1 / 2 = 1/2
Calculate the y-intercept of the regression line (a):
a = \($\bar{y}$\) - b × \($\bar{x}$\) = 7/3 - (1/2) * 2 = 7/3 - 1 = 4/3
Therefore, the equation of the regression line for the given sample data is: y = (1/2) × x + 4/3
Learn more about regression line here:
https://brainly.com/question/30243761
#SPJ11
A cuboid has dimensions x + 2 cm, 2x - 1 cm and 2x + 3 cm. Show that the volume of the cuboid is 4x3 + 12x² + 5x-6 cm³.
Answers
Answer:
\((x+2)(2x-1)(2x+3)\)
Start by multiplying the first two terms:
\((2x^2+3x-2)(2x+3)\)
Now multiply these two terms to prove:
\((4x^3+6x^2+6x^2+9x-4x-6)\)
Simplify:
\((4x^3+12x^2+5x-6)\)
(c) A non-uniform but spherically symmetric charge distribution has a charge density: rho(r)=rho 0
(1−r/R)
rho(r)=0
for r≤R
for r>R
where rho 0
=3Q/πR 3
is a positive constant. Show that the total charge contained in this charge distribution is Q. [4] Show that the electric field in the region r>R is identical to that created by a point charge Q at r=0 [2] Derive an expression for the electric field in the region r≤R. [5]
Answers
To show that the total charge contained in the charge distribution is Q, we integrate the charge density over the entire volume. The charge density is given by:
ρ(r) = ρ₀(1 - r/R) for r ≤ R,
ρ(r) = 0 for r > R,
where ρ₀ = 3Q/πR³.
To find the total charge, we integrate ρ(r) over the volume:
Q = ∫ρ(r) dV,
where dV represents the volume element.
Since the charge density is spherically symmetric, we can express dV as dV = 4πr² dr, where r is the radial distance.
The integral becomes:
Q = ∫₀ᴿ ρ₀(1 - r/R) * 4πr² dr.
Evaluating this integral gives:
Q = ρ₀ * 4π * [r³/3 - r⁴/(4R)] from 0 to R.
Simplifying further, we get:
Q = ρ₀ * 4π * [(R³/3) - (R⁴/4R)].
Simplifying the expression inside the parentheses:
Q = ρ₀ * 4π * [(4R³/12) - (R³/4)].
Simplifying once more:
Q = ρ₀ * π * (R³ - R³/3),
Q = ρ₀ * π * (2R³/3),
Q = (3Q/πR³) * π * (2R³/3),
Q = 2Q.
Therefore, the total charge contained in the charge distribution is Q.
To show that the electric field in the region r > R is identical to that created by a point charge Q at r = 0, we can use Gauss's law. Since the charge distribution is spherically symmetric, the electric field outside the distribution can be obtained by considering a Gaussian surface of radius r > R.
By Gauss's law, the electric field through a closed surface is given by:
∮E · dA = (1/ε₀) * Qenc,
where ε₀ is the permittivity of free space, Qenc is the enclosed charge, and the integral is taken over the closed surface.
Since the charge distribution is spherically symmetric, the enclosed charge within the Gaussian surface of radius r is Qenc = Q.
For the Gaussian surface outside the distribution, the electric field is radially directed, and its magnitude is constant on the surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q,
Simplifying:
E = Q / (4πε₀r²).
This is the same expression as the electric field created by a point charge Q at the origin (r = 0).
To derive an expression for the electric field in the region r ≤ R, we can again use Gauss's law. This time we consider a Gaussian surface inside the charge distribution, such that the entire charge Q is enclosed.
The enclosed charge within the Gaussian surface of radius r ≤ R is Qenc = Q.
By Gauss's law, we have:
∮E · dA = (1/ε₀) * Qenc.
Since the charge distribution is spherically symmetric, the electric field is radially directed, and its magnitude is constant on the Gaussian surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q.
Simplifying:
E = Q / (4πε₀r²).
This expression represents the electric field inside the charge distribution for r ≤ R.
Learn more about charge here:
https://brainly.com/question/18102056
#SPJ11
A car travels at a constant speed of 112 km per hour. Calculate how far the car will travel in 15 minutes.
Answers
The distance, that car will travel in 15 minute, is 28 km.
What is speed, distance and time?The formula used to explain the relationship between speed, distance, and time is speed distance time.
That is speed = distance/ time
So, distance = speed * time
Alternatively, you can calculate the time by dividing the distance traveled by the speed. You can figure out the third input if you know two of the inputs.
Given Speed of car = 112 km per hour
Time = 15 minutes = 15/60 hour
Time = 1/4 hour
Distance traveled by car in 15 minute = Speed of car * time
Distance = 112 * 1/4
Distance = 28 km
To learn more about distance visit:
brainly.com/question/23634231
#SPJ1
I am confused on this problem and am looking for help. If anyone could help me it would be appreciated

Answers
Answer
\(g(x)=-2(x+5)^{2}-3\)0. Horizontal translation 5 units.
,1. Reflection over the x-axis
,2. Vertical compression 2 units
,3. Vertical translation down 3 units
\(y=-(x+5)^2\)Explanation
• Writing the function in completed-square form.
As a ≠ 1, where a is the coefficient of the leading term, to write it in the completed-square form we have to make a = 1:
\(g(x)=-2x^2-20x-53\)\(g(x)=-2(x^2+10x+\frac{53}{2})\)Now we have to take half of the x term and square it and add it to the function as follows:
\(\frac{10}{2}^2=5^2=25\)\(g(x)=-2((x^2+10x+25)+\frac{53}{2}-25)\)Finally, we have a Perfect Squared Trinomial in the left side that we can rewrite as follows, obtaining our function g(x):
\(g(x)=-2(x+5)^2+\frac{3\cdot-2}{2}\)\(g(x)=-2(x+5)^2-3\)As our parent function is:
\(f(x)=x^2\)Then, the transformations that suffered were:
• Horizontal translation to the left 5 units
\(y=(x+5)^2\)• Reflection over the x-axis
\(y=-(x+5)^2\)• Vertical compression 2 units
\(y=-2(x+5)^2\)• Vertical translation down 3 units
\(g(x)=-2(x+5)^{2}-3\)Need Help ASAP
Can someone help me with this problem

Answers
Answer:
Hopes it helps
Step-by-step explanation:
Len
Simplifying
5(3 + -8x) = 0
(3 * 5 + -8x * 5) = 0
(15 + -40x) = 0
Solving
15 + -40x = 0
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-15' to each side of the equation.
15 + -15 + -40x = 0 + -15
Combine like terms: 15 + -15 = 0
0 + -40x = 0 + -15
-40x = 0 + -15
Combine like terms: 0 + -15 = -15
-40x = -15
Divide each side by '-40'.
x = 0.375
Simplifying
x = 0.375
Monty
Simplifying
7 + -2(-5x) = 0
Remove parenthesis around (-5x)
7 + -2 * -5x = 0
Multiply -2 * -5
7 + 10x = 0
Solving
7 + 10x = 0
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-7' to each side of the equation.
7 + -7 + 10x = 0 + -7
Combine like terms: 7 + -7 = 0
0 + 10x = 0 + -7
10x = 0 + -7
Combine like terms: 0 + -7 = -7
10x = -7
Divide each side by '10'.
x = -0.7
Simplifying
x = -0.7
Nailany
Simplifying
7 + -6 + -16x = 0
Combine like terms: 7 + -6 = 1
1 + -16x = 0
Solving
1 + -16x = 0
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-1' to each side of the equation.
1 + -1 + -16x = 0 + -1
Combine like terms: 1 + -1 = 0
0 + -16x = 0 + -1
-16x = 0 + -1
Combine like terms: 0 + -1 = -1
-16x = -1
Divide each side by '-16'.
x = 0.0625
Simplifying
x = 0.0625
Given: g(x) = x-4 and
h(x) = 2x-8.
What are the restrictions on the domain of gh?
Answers
Answer:
Step-by-step explanation:
6
\( T C=\frac{1}{2} e^{2 x}+e^{y}-4 x-2 y \) where \( x= \) units of labour; \( y= \) units of human capital, \( x, y>0 \). a) Calculate \( \frac{\partial T C}{\partial x} \). Interpret this mathematic
Answers
The interpretation of this expression is that the partial derivative of TC w.r.t. x is the rate of change of TC with respect to x, considering all other variables constant. It means if we change one unit of labor, TC will increase by 2e2x - 4 units, considering all other variables remain constant.
T C = 1/2 e2x + ey - 4x - 2ywhere x = units of labor and y = units of human capital, x, y > 0.Calculate:We need to calculate dTC/dx.
Interpretation:First, we need to calculate partial derivative of T C w.r.t. x. We know that partial derivative of a function with respect to one of its variable means to find the derivative of that variable with respect to the function, considering the other variables constant. Hence, it is a rate of change of one variable with respect to other variables considered constant. This is used to find the slope of a surface in a given direction.
The partial derivative of T C w.r.t. x is given as:
∂/∂x (T C)
= 2e2x - 4.∂/∂x (T C)
= 2e2x - 4
The interpretation of this expression is that the partial derivative of TC w.r.t. x is the rate of change of TC with respect to x, considering all other variables constant. It means if we change one unit of labor, TC will increase by 2e2x - 4 units, considering all other variables remain constant.
For more information on partial derivative visit:
brainly.com/question/28751547
#SPJ11
What is the equation of the line that passes through the point (-6, -7) and
has a slope of o?
Answers
Answer:
\(y = 0x - 7\)
Step-by-step explanation:
I'm guessing you mean that the slope is 0??
Equation will then look like this
\(y = 0x + b\)
to get b insert the point into the equation so y will be replaced by -7 and x will be replaced by -6
\( - 7 = 0 \times( - 6) + b\)
\(b = - 7\)
Therefore the equation will be
\(y = 0x - 7\)
Probability.
It has been estimated that about 30% of frozen chickens contain enough salmonella bacteria to cause illness if improperly cooked. A consumer purchases 12 frozen chickens. What is the probability that the consumer will have more than 6 contaminated chickens.
Answers
Answer: 0.0386
Step-by-step explanation:
Given: The probability hat the frozen chickens contain enough salmonella bacteria to cause illness if improperly cooked : p= 0.30
Sample size : n = 12
Let x = Number of contaminated chickens
Here , two outcomes for any chicken (either contaminated or not) , so it follows binomial distribution.
Binomial probability formula:
\(P(X=x) = \ ^nC_x p^x(1-p)^{n-x}\)
The probability that the consumer will have more than 6 contaminated chickens :-
\(P(X>6)=P(X=7)+P(X=8)+P(X=9)+P(X=10)+P(X=11)+P(X=12)\\\\=^{12}C_6(0.3)^6(0.7)^6+^{12}C_7(0.3)^7(0.7)^5+^{12}C_8(0.3)^8(0.7)^4+^{12}C_9(0.3)^9(0.7)^3+^{12}C_{10}(0.3)^{10}(0.7)^2+^{12}C_{11}(0.3)^{11}(0.7)^1+^{12}C_0(0.3)^{12}(0.7)^0\)
\(=0.03860084306\approx0.0386\) (simplified)
Hence, the required probability = 0.0386
Given the following segment lengths find a length of the segment
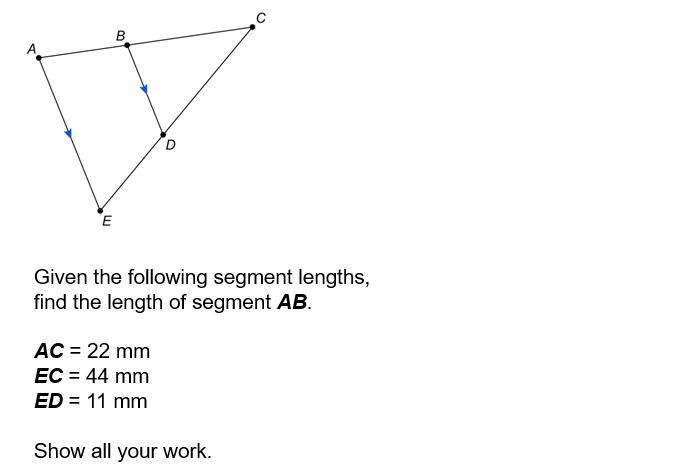
Answers
The length of the line segment AB is 11/2 mm.
What is a triangle?A triangle is a three-sided closed-plane figure formed by joining three noncolinear points.
Based on the side property triangles are of three types they are Equilateral triangle, Scalene triangle, and Isosceles triangle.
We know a line segment parallel to one side of a triangle divides the other two sides in the same ratio.
Therefore, AC/AB = EC/ED.
22/AB = 44/11.
2/AB = 4/11.
4AB = 22.
AB = 11/2.
learn more about triangles here :
https://brainly.com/question/14653505
#SPJ1
At a cookware party, 7 of the 25 items are made of glass. What percent of the cookware items are glass?
Answers
Answer:
28 %
Step-by-step explanation:
Percentage of glass cookware items = no. of glass cookware items / total no. of cook wares * 100
= 7 / 25 * 100
= 28 %
Determine if the sequence below is arithmetic or geometric and determine the
common difference / ratio in simplest form.
14, 10, 6, ...
Answers
Answer:
Step-by-step explanation:
Each term in the sequence is 4 less than the previous term. That indicates an arithmetic sequence, which has the form a(n) = a(1) + d(n -1), where d is the common difference. Here the common difference is -4, and so the appropriate sequence is
a(n) = 14 - 4(n - 1)
the length of a rectangle is 7 inches more than the width. the perimeter is 38 inches. find the length and the width of the rectangle.
Answers
A rectangle's length is 7 inches longer than its width. the perimeter is 38 inches. the length is 13 inches and the width of the rectangle is 12 inches
width = (38 - 14) / 2 = 12 inches
length = (38 - 12) / 2 = 13 inches
to find the length and width of the rectangle given that the length is 7 inches more than the width, and the perimeter is 38 inches, we can use the formula for perimeter (2 x length + 2 x width = perimeter). Plugging in the values given, we get 2 x length + 2 x width = 38. Solving for width, we get width = (38 - 14) / 2 = 12 inches. Plugging this value into the original equation, we get length = (38 - 12) / 2 = 13 inches. Therefore, the length and width of the rectangle are 13 inches and 12 inches, respectively.
Learn more about rectangle here
https://brainly.com/question/29068457
#SPJ4
What is the average rate of change for this exponential function for the interval from x = 2 to x = 4?

Answers
Answer:
The average rate of change over the interval is 120
Step-by-step explanation:
For a function f(x) the average rate of change over an interval [a,b] is given as;
f(b)-f(a)/b-a
in this case, a is 2 and b is 4
f(b) is 256 and f(a) is 16
Substituting these values in the equation for rate of change, we have;
(256-16)/(4-2) = 240/2 = 120
What was the average number of miles walked per day. (Round to the nearest tenth)

Answers
Ex.) for 2 miles, you would add it as 2+2+2 and continue for all except 0(because they didn’t walk any miles)
Then you are left with 57 miles in total and you divide by the 19 participants
57/19=3
(4) consider three sheep M1,M2,M3 playing leapfrog. We (4). will place the sheep in a flan and characterize them by their coordinates M1=(x10,y10),M2=(x20,y20),M3=(x30,y30) the rules of the game are as follows: - M1 jump over M2 and the new fosition of the first sheep is the mirrol image of M1 by the center symmetry M2. - M M2 jumps above M3 and the new position of the second sheep is the symmetric of M2 by the centas symmetry M3 - M3 Jumps Above M1 and the new position of the second sheep is the symmetry of M by the symmetry of center M1 (Attention M1 has ofready fumped, the symmetry is therefore made with to its mew Position!). We continue the process by following the previous rustes, we denate by (x1m,y1n),(x2n,y2m) and (x3m,y3n) the coordinates of the shcep M1,M2 and M3 after m iterations. Let xm and ym be the vectors defined by xn=⎝⎛x1mx2mx3m⎠⎞ym=⎝⎛y1my2my3m⎠⎞ 1. Give a link between xn+1 and xn for all n∈N. Same question for ym+1 and ym. 2. Deduce a link between xn and x0. Same question for yn and y0 3. Determine an explicit formula for x1n,x2n and x3n and function of x10,x20 and x30 4. Under what condition(s) on the imitial fositions of M1,M2 and M3 con the sheep fump to infinity in a bounded space of the plane?
Answers
The link between xn+1 and xn for all n ∈ N is xn+1 = 2xn - xn-1. The link between yn+1 and yn is yn+1 = 2yn - yn-1. The link between xn and x0 is xn = 2x0 - xn-1. The link between yn and y0 is yn = 2yn - yn-1.
The explicit formula for x1n, x2n, and x3n is as follows:
x1n = 2x10 - x1(n-1)
x2n = 2x20 - x2(n-1)
x3n = 2x30 - x3(n-1)
The sheep can jump to infinity in a bounded space of the plane if and only if the initial positions of M1, M2, and M3 form an equilateral triangle.
The link between xn+1 and xn can be found by considering the symmetry of the leapfrog game. When M1 jumps over M2, the new position of M1 is the mirror image of its previous position with respect to M2. This means that the x-coordinate of M1 will be the same as the x-coordinate of M2, but the y-coordinate will be the negative of the y-coordinate of M2.
The link between yn+1 and yn can be found by considering the symmetry of the leapfrog game. When M2 jumps over M3, the new position of M2 is the mirror image of its previous position with respect to M3. This means that the y-coordinate of M2 will be the same as the y-coordinate of M3, but the x-coordinate will be the negative of the x-coordinate of M3.
The explicit formula for x1n, x2n, and x3n can be found by using the recursive formulas for xn+1 and xn.
The condition for the sheep to jump to infinity in a bounded space of the plane can be found by considering the distance between the sheep. If the initial positions of M1, M2, and M3 form an equilateral triangle, then the distance between the sheep will remain constant. This means that the sheep will continue to jump forever, and they will never reach the boundary of the space.
To learn more about equilateral triangle click here : brainly.com/question/12990950
#SPJ11
A surveyor randomly interviewed 34,572 people who live in Scotland to gather information on whether national healthcare is accomplishing its goals.
Part A: What are the population and sample in this survey? (4 points)
Part B: The survey found that 70% of smokers and 87% of non-smokers visited a family doctor at least once in the past year. Do you think these approximations of the sample are close to approximations of the entire population? Explain. (6 points)
I NEED PART B
Answers
Answer:
Part A
Here the entire population is the total number of people who live in Scotland and the sample considered in this survey is the randomly chosen 34,572 people.
Part B
The approximations made out of the sample cannot be considered same as that of the entire population. Because here, only a random sample of 34,572 is taken whereas the total population here is the people who live in the Scotland, which can be quite large sample. The patient details recorded are used for survey. So in the sample surveyed we do not have the data about the rest of the population. The approximations made out of the sample become same as that of the entire population only if the entire population number is near to the randomly collected sample.
A theater has 1,464 seats. The seats are arranged into 62 equal-sized "regular" sections plus one "premium" front-row section. How many seats are in a regular section? How many seats are in the premium front-row section? Explain.
Answers
In the theater, that have 1,464 seats.
1426 seats are in "regular" sections
38 seats are "premium" front-row section
How to find the number of seats in the "regular" sectionsThe seat arrangement is solved by division. In this case the 62 equal spaced is the divisor while the number of seats is the in each row is the quotient
The division is as follows
1464 / 62
= 23 19/31
The number of seats in the regular section is 23 * 62 = 1426
The remainder will be arranged in premium front row
using equivalent fractions
19 / 31 = 38 / 62
the remainder is 38 and this is the seat for the premium front row section
OR 1464 - 1426 = 38 seats
Learn more about division here:
https://brainly.com/question/29401139
#SPJ1
i’m very confused on this can someone help?

Answers
Answer:
(x,y) -> (5,4)
Step-by-step explanation:
there is a positive slope.
Right triangle XYZ has right angle Z. If the sin(X)=1213
, what is the cos(X)
Answers
Given:
Right triangle XYZ has right angle Z.
\(\sin(x)=\dfrac{12}{13}\)
To find:
The value of \(\cos x\).
Solution:
We know that,
\(\sin^2(x)+\cos^2(x)=1\)
\(\cos^2(x)=1-\sin^2(x)\)
\(\cos(x)=\pm\sqrt{1-\sin^2x}\)
For a triangle, all trigonometric ratios are positive. So,
\(\cos(x)=\sqrt{1-\sin^2x}\)
It is given that \(\sin(x)=\dfrac{12}{13}\). After substituting this value in the above equation, we get
\(\cos(x)=\sqrt{1-(\dfrac{12}{13})^2}\)
\(\cos(x)=\sqrt{1-\dfrac{144}{169}}\)
\(\cos(x)=\sqrt{\dfrac{169-144}{169}}\)
\(\cos(x)=\sqrt{\dfrac{25}{169}}\)
On further simplification, we get
\(\cos(x)=\dfrac{\sqrt{25}}{\sqrt{169}}\)
\(\cos(x)=\dfrac{5}{13}\)
Therefore, the required value is \(\cos(x)=\dfrac{5}{13}\).
(Ignore this) I mean you can get the points if u want lol, I’m trying to test something.
Answers
Answer:
Answer:
Lol hi
Whathca tryin to test?
Step-by-step explanation:
Llololoo
Step-by-step explanation:
Answer:
Okok
Step-by-step explanation:
➊➋➌
❃
☟
➜↷↶
≅
lolololololol
AOB is a sector of a circle, centre O.
50°
6 cm
B
Not to scale
Calculate the length of arc AB, correct to 3 significant figures.
(3 marks)

Answers
Answer: 5π/3 (5,236)
Step-by-step explanation: Length of the whole circle arc is 2πr, in this case it is 12π. 50° is 50/360 = 5/36 part of the arc, so we can multiply 12π by 5/36 to get an answer. 12π * 5/36 = 5π/3.
How many gallons each of 30% alcohol and 5% alcohol should be mixed to obtain 25gal of 25% alcohol?

Answers
Let x be the amount of the 30% alcohol and let y be the amount of 5% alcohol.
We want the total amount to by 25 gal, then we have:
\(x+y=25\)We also want the resulting mix to be 25% alcohol, this is 0.25 in decimal form; also we know that the first type of alcohol is 30% and the second is 5%, then we have:
\(\begin{gathered} 0.3x+0.05y=0.25(25) \\ 0.3x+0.05y=6.25 \end{gathered}\)Hence we have the system of equations:
\(\begin{gathered} x+y=25 \\ 0.3x+0.05y=6.25 \end{gathered}\)To solve the system we solve the first equation for y:
\(y=25-x\)then we plug this value of y in the second equation:
\(\begin{gathered} 0.3x+0.05(25-x)=6.25 \\ 0.3x+1.25-0.05x=6.25 \\ 0.25x=6.25-1.25 \\ 0.25x=5 \\ x=\frac{5}{0.25} \\ x=20 \end{gathered}\)Once we have the value of x we plug it in the expression we found for y:
\(\begin{gathered} y=25-20 \\ y=5 \end{gathered}\)Therefore, the mixture will have 20 gallons of 30% alcohol and 5 gallons of 5% alcohol.
A ladder reaches 2 m up a wall. the foot of the ladder is 0.4 m from the wall. for safety reasons, the slope should be between 6.3 and 9.5. is this ladder within the safe range?
Answers
Answer:
No, the ladder is not within the safe range because the slope is 5.
Step-by-step explanation:
To solve, find the slope of the ladder using the slope formula and check if the slope is between 6.3 and 9.5.
What is slope?
Slope is how steep a line is. In this case, the line is the ladder. If the ladder is too steep, them it is not safe.
How do we calculate slope?You can calculate slope using the following formula:
\(slope = \frac{rise}{run}\)
Rise means how faraway vertically, or how high up the ladder is.
Run means the how faraway horizontally, or from the wall the ladder is.
Slope of the ladderLet's calculate slope using the formula.
\(\displaystyle {slope=\frac{rise}{run}}\)
\(\displaystyle {slope=\frac{2\ m}{0.4\ m}}\) Substitute the values, 2m for rise, 0.4m for run.
\(\displaystyle {slope=5}\) Final answer
Is the ladder safe?The question tells us that a safe ladder has a slope of 6.3 to 9.5. The slope, 5, is not between that range. Therefore, the ladder is not safe.
what is 7/9 divided by 6/8
Answers
Answer: \(\frac{28}{27}\) or \(1\frac{1}{27}\)
Step-by-step explanation:
\(\frac{7}{9} /\frac{6}{8} = \frac{7}{9}(\frac{8}{6})\)
\(\frac{7}{9} (\frac{8}{6} ) = \frac{28}{27}\)
\(\frac{28}{27} = 1 \frac{1}{27}\)
What is the weight of a square if a triangle weighs 4 grams?
Answers
Answer:
8 grams
Step-by-step explanation:
a triangle is half a square
Given the scatter plot, choose the function that best fits the data.
scatter plot with data points that form an upward curve staring at the origin and continuing to the right
f(x) = 2x
f(x) = 2x
f(x) = −2x
f(x) = 2x2
Answers
Hey love! <3
Answer:
f(x) = 2^x
Step-by-step explanation:
You can see the scatter plot increase by 2^x just by observations of the graph and statistic residuals (if you calculated them!)
Hope this brightens up your day/night! ╰(◡‿◡✿╰) Sincerely, Kelsey from Brainly.
~ #LearnWithBrainly ~
The function that best fits the data is \(y = 2^x\)
From the graph, we have the following ordered pairs
(0,1) and (1,2)
The graph represents an exponential function.
An exponential function is represented as:
\(y = ab^x\)
At (0,1), we have:
\(ab^0 = 1\)
\(a =1\)
At (1,2), we have:
\(ab^1 = 2\)
\(ab =2\)
Substitute 1 for a
\(1 * b = 2\)
\(b =2\)
Recall that:
\(y = ab^x\)
So, we have:
\(y = 1 * 2^x\)
\(y = 2^x\)
Hence, the function that best fits the data is \(y = 2^x\)
Read more about exponential functions at:
https://brainly.com/question/11464095
please help i dont know how to solve

Answers
Answer:
shouldn't it be all the same answer since it looks like a equilateral triangle