Answers
Answer: Option (4)
Step-by-step explanation:
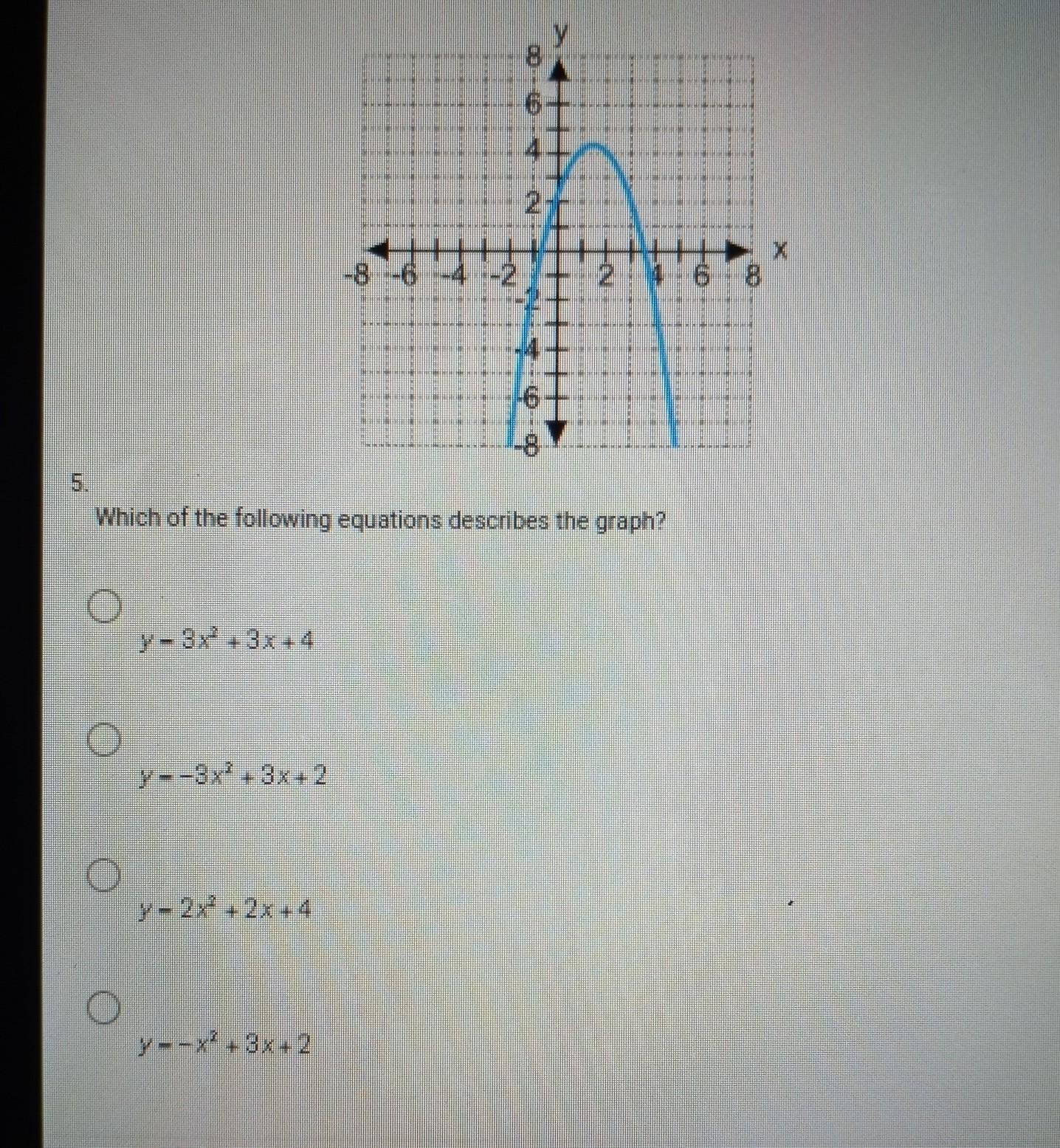
The graph has a y-intercept of 2.
Eliminate options (1) and (3).The graph passes through (2,4).
Eliminate option (2).This leaves option (4) as the correct answer.
Related Questions
Knowing that ΔBIG ≅ ΔFNS, an angle pair that is NOT necessarily congruent is:
Knowing that ΔDAL ≅ ΔEKS, a side pair that is NOT necessarily congruent is:

Answers
solutions:
1) G ≅ F
2) DA ≅ ES
Explanation:
Q)1
ΔBIG ≅ ΔFNS
pairs that are congruent:
B ≅ FI ≅ NG ≅ SFrom the list given,
→ G ≅ F is not necessarily congruent.
Q)2
ΔDAL ≅ ΔEKS
pairs that are congruent:
DA ≅ EKAL ≅ KSDL ≅ ESFrom the list given,
DA ≅ ES is not necessarily congruent.
Usually the congruence is done according to naming
So
∆BIG≅∆FNS<B=F
<I=<N
<G=<S
Option A#2
Check the naming
∆DAL≅∆EKSSo
DA=EK
And DA may not be equal to ESSo option D
A cone with radius 9 cm has the same surface area as a cylinder with a radius of 6 cm and height 18 cm. What is the height of the cone to the nearest tenth?
Answers
Answer: 3.5 cm
Step-by-step explanation:
SA for cone = \(\pi\)rs + \(\pi\)r² r=radius=9 s=slant height (not height)
A(cone) = 9\(\pi\)s + 81\(\pi\)
SA for a cylinder = 2\(\pi\)rh +2\(\pi r^{2}\) r=6 h = 18
A(cyl) = 2(\(\pi\))(6)(8) + 2(\(\pi\))6²
= 96\(\pi\) + 72\(\pi\)
=168\(\pi\)
Set the 2 areas equal to each other to solve for slant height
9\(\pi\)s + 81\(\pi\) = 168\(\pi\)
9\(\pi\)s=87\(\pi\)
s=87/9
this is slant height, now you use pythagorean to solve for h
(87/9)²=9²+h²
h=3.5
The prices of 4 jars of pasta sauce are shown below
Jar 1 : $1.60 Jar 2: $2.40
Jar 3: $2.64
Jar 4: $2.88
Which jar of pasta sauce has the greatest unit
price?
A. Jar 1
B. Jar 2
C. Jar 3
D. Jar 4
Answers
Answer:
Jar 4
Step-by-step explanation:
Jar 4 it has to be 20 charc
wall posters are usually sold curled up in cylindrical cardboard tubes. if the length of the tube is 84.5cm and the diameter of the tube is 2.40 cm, what is the area of the poster in cm2?
Answers
If the length of the tube is 84.5cm and the diameter of the tube is 2.40 cm, then area of poster is 636.7 cm² ~ 637 cm²
Given that ;
Length of the cylinder = 84.5 cm
Diameter of the cylinder = 2.40 cm
Then the radius is 1.20 cm
When the poster is uncurled it is in rectangle shape so, length of the poster is 84.5cm.
When poster is curled in cylinder, circumference of circle is breadth of poster = 2πr = 2(22/7)1.2 = 7.53 cm
So the area of poster is length × breadth
Area = 84.5cm × 7.53cm
Area = 636.7 cm²
Hence the area of poster is 636.7 cm² ~ 637 cm²
Visit here to learn more about rectangle: https://brainly.com/question/29123947
#SPJ4
3. The diagram on the right shows the pattern drawn on a Cartesian plane. The final line on the plan is parallel to the y-axis and passes through x = -10. Find the sum of the length of the overall pattern.

Answers
The sum of the length of the overall pattern in the given cartesian coordinate is calculated as; 44
How to find the lengths of a cartesian?We are told that The final line on the plan is parallel to the y-axis and passes through x = -10
Now, looking at the pattern, the lengths of each side are as follows;
1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5, 6, 6.5
Thus, the sum of the length of the overall pattern is calculated as;
1.5 + 2 + 2.5 + 3 + 3.5 + 4 + 4.5 + 5 + 5.5 + 6 + 6.5 = 44
Therefore we can conclude from all the deductions and calculations above that the sum of the length of the overall pattern in the given cartesian coordinate is calculated to be; 44
Read more about Cartesian plane at; https://brainly.com/question/2141683
#SPJ1
Johnny starts run at the 2 mile mark and runs 4 miles per hour. Javier starts at the 6 mile mark and runs 2 miles per hour. How long until Johnny catches up with Javier?
Answers
Answer:
2 hours
Step-by-step explanation:
A quantity with an initial value of 3400 grows exponentially at a rate of 1. 5% every 3 minutes. What is the value of the quantity after 1. 65 hours, to the nearest hundredth?
Answers
To the nearest tenth, 5,557.23 is the value of the quantity at 1. 65 hours when a 3400-valued quantity increases exponentially at a rate of 1.5% every three minutes.
Given that,
A 3400-valued quantity increases exponentially at a rate of 1.5% every three minutes.
We have to find to the nearest tenth, what is the value of the quantity at 1. 65 hours.
We know that,
Present value= 3,400
Growth rate (g)= 1.5% every 3 minutes
Number of periods (n)= (1.65×60) / 3= 33
To calculate the future value,
We know
Future Value= PV×(1+g)ⁿ
Future Value= 3,400×(1.015³³)
Future Value= 5,557.23
Therefore, To the nearest tenth, 5,557.23 is the value of the quantity at 1. 65 hours when a 3400-valued quantity increases exponentially at a rate of 1.5% every three minutes.
To learn more about minutes visit: https://brainly.com/question/15600126
#SPJ4
Laura conduce un patinete eléctrico a 45 km/h cuando no llueve y a 30 km/h cuando llueve. Hoy hacía sol por la mañana y llovía por la tarde e hizo un total de 24 km en 40 minutos. ¿Cuántos minutos condujo por la tarde?
Answers
If today it was sunny in the morning and raining in the afternoon, and Laura traveled a total of 24 km in 40 minutes, then she is calculated to have rode the electric scooter for 24 minutes in the afternoon.
Let's assume that Laura rode her scooter for x minutes in the morning and for (40 - x) minutes in the afternoon.
In the morning, she traveled a distance of 45 × (x/60) km.
In the afternoon, she traveled a distance of 30 × ((40-x)/60) km.
The total distance traveled is 24 km, so we can set up the equation:
45 × (x/60) + 30 × ((40-x)/60) = 24
Multiplying both sides by 60, we get:
45x + 30(40-x) = 1440
Simplifying and solving for x, we get:
15x + 1200 = 1440
15x = 240
x = 16
Therefore, Laura rode her scooter for (40-16) = 24 minutes in the afternoon.
Learn more about speed and distance :
https://brainly.com/question/29775794
#SPJ4
The question is :
Laura rides an electric scooter at 45 km/h when it is not raining and at 30 km/h when it is raining. Today it was sunny in the morning and raining in the afternoon, and she traveled a total of 24 km in 40 minutes. How many minutes did she ride in the afternoon?
Let f be the function with first derivative given by f'(x)=(3-2x-x^2) sin(2x-3). How many relative extrema does have on the open interval -4
(A) Two
(B) Three
(C) Four
(D) Five
(E))Six
Answers
The quadrants that satisfy the condition xy > 0 are quadrant I and quadrant III.
Quadrant I is the top-right quadrant, where both the x-coordinate and y-coordinate are positive. In this quadrant, the product of x and y will also be positive, since two positive numbers multiplied together always result in a positive number.
Quadrant III is the bottom-left quadrant, where both the x-coordinate and y-coordinate are negative. In this quadrant, the product of x and y will also be positive, since two negative numbers multiplied together also result in a positive number.
Quadrants II and IV do not satisfy the condition, since in quadrant II, the x-coordinate is negative while the y-coordinate is positive, resulting in a negative product. Similarly, in quadrant IV, the x-coordinate is positive while the y-coordinate is negative, also resulting in a negative product.
to know more about quadrants, click: brainly.com/question/30979352
#SPJ11
given the line 3x+4y=3 and y=mx+8 intersect at a 45° angle, find m
Answers
Answer:
We can begin by finding the slope of the line 3x+4y=3 by rearranging it into slope-intercept form, y=mx+b:
4y = -3x + 3
y = (-3/4)x + 3/4
Thus, the slope of this line is -3/4.
Since the line y=mx+8 intersects the first line at a 45° angle, we know that the product of their slopes must be -1 (since the tangent of a 45° angle is 1). Therefore, we can set up the equation:
(-3/4)(m) = -1
Solving for m, we get:
m = 4/3
Therefore, the value of m that would make y=mx+8 intersect the line 3x+4y=3 at a 45° angle is 4/3.
Shaylyn measured her house as 5 meters tall.Which of these is an equivalent measurement
A. 0.3 miles
B. 7.3 yards
C. 16.4 feet
D. 27.2 inches
Answers
Solve the system using substitution (1 point)
x + y = 8
y = 3x
(A). (4, 12)
(B). (2, 6)
(C). (1/2, 3/2)
(D). (-4, -12)
Answers
The solution to the system is x = 2 and y = 6, represented as the ordered pair (2, 6). This corresponds to option (B) in the answer choices.
To solve the system using substitution, we'll substitute the value of one variable from one equation into the other equation and solve for the remaining variable.
Given the system:
x + y = 8
y = 3x
Substituting the value of y from the second equation into the first equation, we have:
x + (3x) = 8
4x = 8
x = 2
Now, substitute the value of x into the second equation to solve for y:
y = 3(2)
y = 6
Therefore, the solution to the system is (2, 6). Option (B) is the correct answer.
To know more about variable click here
brainly.com/question/2466865
#SPJ11
Simplify - 5-V-44.
O-5-4 11
O-5-411
O-5-21 11
0-5-2 111

Answers
On simplification we get,
\( \sqrt{ - 121} \)\( \sqrt{ {i}^{2} \times 121} \)\(i \times 11\)\(11i\)correct option is B
is my answer correct or is it wrong


Answers
Answer:
Your answer is wrong, H is the correct answer.
Step-by-step explanation:
The Triangle Inequality Theorem states that the sum of any 2 sides of a triangle must be greater than the measure of the third side. Note: This rule must be satisfied for all 3 conditions of the sides.
will give brainliest

Answers
Answer:
40⁰
Step-by-step explanation:
Main principles:
1.Alternate angles equal
2.Vertically opposite angles are equal
If angle 2 is 40⁰, then using the second principle,angle 3 is also 40⁰
Then, using the first principle,(alternate angles/angles that form any variation of "z"), angle 6 is also 40⁰.
There are other ways to do this like using co-interior angles, straight angles and other methods, these are the easiest to understand
Pls help me with this question

Answers
Answer: It's the third rectangle
Step-by-step explanation: If you cut from the vertex vertically it would be a triangle but if you cut a pyramid horizontally its either a square or rectangle.
a statistics professor asked students in a class their ages. based on this information, the professor states that the average age of all the students in the university is 24 years. this is an example of a. an experiment. b. an observational study. c. statistical inference. d. descriptive statistics.\
Answers
The correct option is statistical inference (b).
The professor uses sample data from the population to determine the average age. Anytime inferential statistics or statistical inference is used to make inferences from samples.
Instead of gathering data from the entire institution, the professor took age samples from a class and used those data to draw conclusions about the entire university.
Descriptive statistics in statistics help you describe the facts, whereas inferential statistics assist you in drawing conclusions from the data.
Data from the sample are used in inferential statistics, which allows you to generalise about the population.
Inference generally refers to "guessing," which involves drawing conclusions about something.
So, drawing conclusions about the population is what is meant by statistical inference. It makes use of a number of statistical analytic tools to draw a conclusion about the population.
Therefore, the correct option is statistical inference.
For more such questions on Statistical inference
https://brainly.com/question/13752289
#SPJ4
Edward works as a waiter, where his monthly tip income is normally distributed with a mean of $2,000 and a standard deviation of $350. Use this information to answer the following questions. Record yo
Answers
The probability that Edward’s monthly tip income exceeds $2,350 is 0.8413.
Given that Edward works as a waiter, where his monthly tip income is normally distributed with a mean of $2,000 and a standard deviation of $350.
The z score formula is given by;`z = (x - μ) / σ`
Where; x is the raw scoreμ the mean of the populationσ is the standard deviation of the population.
The probability that Edward’s monthly tip income exceeds $2,350 is to be found.`z = (x - μ) / σ``z = (2350 - 2000) / 350``z = 1`
The value of z is 1.
To find the area in the right tail, use the standard normal distribution table.
The table value for z = 1.0 is 0.8413.
Therefore, the probability that Edward’s monthly tip income exceeds $2,350 is 0.8413.
Know more about probability here:
https://brainly.com/question/251701
#SPJ11
A and B are two events. Let P(A) = 0.65, P (B) = 0.17, P(A|B) = 0.65 and P(B|4) = 0.17 Which statement is true?
1. A and B are not independent because P(A|B) + P(A) and P(B|4) + P(B).
2. A and B are not independent because P (A|B) + P(B) and P(B|4) + P(A)
3. A and B are independent because P (A|B) = P(A) and P(BIA) = P(B).
4. A and B are independent because P (A|B) = P(B) and P(B|A) = P(A).
Answers
Answer:
the statement that is true is: A and B are not independent because P(AIB) + P(B) is not equal to P(BIA) + P(A)
Step-by-step explanation:
ur welcome
Can u answer this u are just making a equation and answering it?

Answers
reasoning:
34 - 10 = 24
24 / 2 = 12
Answer:
48 spinners
Step-by-step explanation:
Since he recently added 10 to his collection to make 34, we are going to start by subtracting 10.
34-10 = 24
Now, we understand that he sold half his set. So taking this number (24) we will multiply the "set" by 2.
24x2= 48
if this is right, and you like my answer, please mark me brainliest !! thx <3 !!
.In order to increase the value of the F statistic, which of the following must occur?
a. MSwithin > MSbetween
b. MSwithin = MSbetween
c. MSwithin < MSbetween
d. Ratio = 1
Answers
If MSwithin is smaller than MSbetween, then increasing MSwithin and/or decreasing MSbetween will lead to an increase in the F statistic.
How the F statistic is calculated?The F statistic is calculated by dividing the variance between groups (MSbetween) by the variance within groups (MSwithin). Therefore, to increase the value of the F statistic, either the numerator (MSbetween) needs to increase, or the denominator (MSwithin) needs to decrease.
So, the answer is:
a. MSwithin > MSbetween
If the variance within groups (MSwithin) is reduced or the variance between groups (MSbetween) is increased, the F statistic will increase. Therefore, if MSwithin is smaller than MSbetween, then increasing MSwithin and/or decreasing MSbetween will lead to an increase in the F statistic.
Learn more about statistic
brainly.com/question/31538429
#SPJ11
the null hypothesis is always a statement about what?
Answers
The null hypothesis is always a statement about the population parameter or the absence of a relationship or difference between variables in a statistical hypothesis test. It is typically denoted as "H0" and assumes no effect or no difference exists.
The null hypothesis can take different forms depending on the specific research question. For example, in a study comparing the mean scores of two groups, the null hypothesis might state that the means are equal. In a correlation study, the null hypothesis could assert that there is no correlation between variables.
The null hypothesis acts as a baseline for comparison in hypothesis testing. Researchers aim to gather evidence against the null hypothesis to support an alternative hypothesis. Statistical analysis helps determine the likelihood of observing the obtained data if the null hypothesis were true.
By specifying a null hypothesis, researchers can objectively evaluate the evidence and draw conclusions about the relationship or difference they are investigating.
In summary, the null hypothesis is a statement about the population parameter or lack of relationship/difference, which serves as a reference point for hypothesis testing. It helps researchers assess evidence and draw conclusions based on statistical analysis.
Know more about null hypothesis here,
https://brainly.com/question/30821298
#SPJ11
Cooling towers are used to remove or expel heat from a process. A cooling tower's walls are modeled by where the measurements are in meters. What is the width of the cooling tower at the base of the structure
Answers
The width of the cooling tower is 36 meters.
What is a cooling tower?A cooling tower is a vent that is built for the purpose of releasing waste heat back to the atmosphere.
Now we can model the system using; x²/324 - (y² - 90)²/1600. Thus, the width can be obtained from;
2 × ✓324
= 2 × 18
= 36 meters
Learn more about cooling tower:https://brainly.com/question/26654522
#SPJ1
Missing parts;
Cooling towers are used to remove or expel heat from a process. A cooling tower's walls are modeled by x squared over 324 minus quantity y minus 90 end quantity squared over 1600 equals 1 comma where the measurements are in meters. What is the width of the cooling tower at the base of the structure? Round your answer to the nearest whole number.
36 meters
48 meters
80 meters
89 meters
There are 8 players on a tennis team. The team is planning to play in a doubles tournament. How many different groups of players of 2 players can the coach make, if the position does not matter?
28
64
20,160
40,320
Answers
Answer:
the answer should be 28 ..
Answer:
The answer is 28!!!
Step-by-step explanation:
Use the combination formula to solve:
\(C = \frac{n!}{r!(n-r)!}\)
where
n = 8
and
r = 2
\(C = \frac{8!}{2! ~*~ 6!} = 28\)
I also got it right, look at the pic. Hope this helps!! :)

Solve for x.
2(x−3 1/2)=10 3/4
Enter your answer as a mixed number in simplest form in the box.
Answers
Answer:
x = 71/8
Step-by-step explanation:
Solve for x:
2 (x - (3 + 1/2)) = 10 + 3/4
Put 3 + 1/2 over the common denominator 2. 3 + 1/2 = (2×3)/2 + 1/2:
2 (x - (7/2)) = 10 + 3/4
2×3 = 6:
2 (x - (1/2 6 + 1/2)) = 10 + 3/4
6/2 + 1/2 = (6 + 1)/2:
2 (x - (7/2)) = 10 + 3/4
6 + 1 = 7:
2 (x - 1/2 7) = 10 + 3/4
Put each term in x - 7/2 over the common denominator 2: x - 7/2 = (2 x)/2 - 7/2:
2 ((2 x)/2 - 7/2) = 10 + 3/4
(2 x)/2 - 7/2 = (2 x - 7)/2:
2 (1/2 (2 x - 7)) = 10 + 3/4
(2 (2 x - 7))/2 = 2/2×(2 x - 7) = 2 x - 7:
(2 x - 7) = 10 + 3/4
Put 10 + 3/4 over the common denominator 4. 10 + 3/4 = (4×10)/4 + 3/4:
2 x - 7 = ((4×10)/4 + 3/4)
4×10 = 40:
2 x - 7 = 40/4 + 3/4
40/4 + 3/4 = (40 + 3)/4:
2 x - 7 = ((40 + 3)/4)
40 + 3 = 43:
2 x - 7 = 43/4
Add 7 to both sides:
2 x + (7 - 7) = 43/4 + 7
7 - 7 = 0:
2 x = 43/4 + 7
Put 43/4 + 7 over the common denominator 4. 43/4 + 7 = 43/4 + (4×7)/4:
2 x = (43/4 + (4×7)/4)
4×7 = 28:
2 x = 43/4 + 28/4
43/4 + 28/4 = (43 + 28)/4:
2 x = ((43 + 28)/4)
43 + 28 = 71:
2 x = 71/4
Divide both sides by 2:
x = (71/2)/4
4×2 = 8:
Answer: x = 71/8
Please answer, I will give brainliest

Answers
Step-by-step explanation:
Hey, there!!
Let's look in your question,
Firstly Mr.Ingerson was in Ghana and bought it in 35000 cedi for a djembedrum.
At that time 1 US dollar= 7000 Cedi.
He paid 35000 cedi.
Us dollar for 35000 cedi = 35000/7000 $.
So, he had bought it in $5.
now,
At present,
The value of 1$ is 5.79 cedi.
As he bought it on same value,
5$ is equal to 5.79×5
= 28.95 cedi.
{ here, as it told that it was bought in same value its value is $5 only but, as the value of $ will be changed into 5.79}.
Hope it helps...
structions: Drag and drop the correct name for each angle. Each angle has more than one name so be sure to identify all the correct names

Answers
Answer:
1) I, 4, HIJ
2) G, 1, HGF
3) J, 2, IJK
Step-by-step explanation:
A manufacturer determines that the number of toys it can sell is given by the formula
T=-4p2+160p-305, where p is the price of the toys in dollars.
At what price will the manufacturer sell the maximum number of toys and what is the maximum
number of toys that can be sold?
Answers
Answer:
The price where the manufacture sells the maximum number of toys is $20
Step-by-step explanation:
The given equation for that represents the number of toys the manufacturer can sell is given as follows;
T = -4·p² + 160·p - 305
Where;
p = The price of the toys in dollars
At the point where the manufacture sells the maxim number of toys on the graph of the equation T = -4·p² + 160·p - 305, which is the top of the graph, the slope = 0
Therefore, at the maximum point;
The slope = 0 = dT/dp = d(-4·p² + 160·p - 305)/dp = -8·p + 160
∴ -8·p + 160 = 0
160 = 8·p
8·p = 160
p = 160/8 = 20
The price where the manufacture sells the maximum number of toys is = p = 20 dollars
PLEASE HELP!! Graph the transformation on the graph picture, no need to show work or explain.

Answers
A graph of the polygon after applying a rotation of 90° clockwise about the origin is shown below.
What is a rotation?In Mathematics and Geometry, a rotation is a type of transformation which moves every point of the object through a number of degrees around a given point, which can either be clockwise or counterclockwise (anticlockwise) direction.
Next, we would apply a rotation of 90° clockwise about the origin to the coordinate of this polygon in order to determine the coordinate of its image;
(x, y) → (y, -x)
A = (-4, -2) → A' (-2, 4)
B = (-3, -2) → B' (-2, 3)
C = (-3, -3) → C' (-3, 3)
D = (-2, -3) → D' (-3, 2)
E = (-2, -5) → E' (-5, 2)
F = (-3, -5) → F' (-5, 3)
G = (-3, -4) → G' (-4, 3)
H = (-5, -4) → H' (-4, 5)
I = (-5, -3) → I' (-3, 5)
J = (-4, -3) → J' (-3, 4)
Read more on rotation here: brainly.com/question/28854313
#SPJ1

The congruent sides of an isosceles triangle are each 50
centimeters. The vertex angle measures 40°. What is the
length of the base of the triangle? Round to one decimal
place.
Select one:
O 34.2 cm
17.1 cm
28.3 cm
20.6 cm
Answers
The length of the base of the triangle is approximately 34.2 cm.
To find the length of the base of the isosceles triangle, we can use the cosine rule.
The cosine rule states that in a triangle with sides of lengths a, b, and c, and the angle opposite to side c is A, we have:
c² = a² + b² - 2ab × cos(A)
In this case, the congruent sides of the isosceles triangle are each 50 centimeters, so we have:
a = b = 50 cm
The vertex angle measures 40°, so A = 40°. Let's calculate the length of the base (c):
c² = 50² + 50² - 2 × 50 × 50 × cos(40°)
Now we can solve for c:
c² = 2500 + 2500 - 5000 × cos(40°)
c² = 5000 - 5000 × cos(40°)
c² = 5000 × (1 - cos(40°))
c = sqrt(5000 × (1 - cos(40°)))
Using a calculator, we find that c ≈ 34.2 cm.
Therefore, the length of the base of the triangle is approximately 34.2 cm.
So, the correct answer is: 34.2 cm
Learn more about cosine rule click;
https://brainly.com/question/28716982
#SPJ1