The area of a rectangle is 8811m if the width of the garden is 89 m what’s the length
Answers
The length of the garden is 99 m.
What’s the length?The formula for the area of a rectangle is:
Area = Length x Width
We are given that the area of the rectangle is 8811 \(m^{2}\) and the width is 89 m. Substituting these values into the formula, we get:
8811 \(m^{2}\) = Length x 89 m
To solve for the length, we can divide both sides of the equation by 89 m:
Length = 8811 \(m^{2}\) / 89 m
Simplifying, we get:
Length = 99 m
Therefore, the length of the garden is 99 m.
to know more about rectangle
brainly.com/question/29123947
#SPJ1
Related Questions
AB/DC = AC/CE and AC||CD
Prove: triangle abc is similar to triangle cde
Answers
Triangle ABC is indeed similar to Triangle CDE by the SAS (Side-Angle-Side) Congruence Postulate.
How are the triangles congruent ?Assume that we have the following to prove congruence:
AB/DC = AC/CE (proportional sides)
AB || CD (parallel lines)
This means that angle ABC is congruent to angle CDE.
Looking at this, we can infer that Side AB is proportional to side DC. We also see that Angle ABC is the same as Angle CDE.
Going by the SAS Congruence theorem, Triangle ABC is indeed similar to Triangle CDE because two sides of the triangle are similar and one angle is congruent.
Find out more on congruence at https://brainly.com/question/18922904
#SPJ1
ALGERBA 1 (SIMPLIFY ) PLS HELP :)) <3

Answers
Number 2 D
A cake is a rectangular prism with height 3 inches and bases 8 inches by 10 inches. Samantha wants to apply frosting to the sides and the top of the cake. What is the surface area of the part of the cake that will have frosting?
Answers
Answer:
268
Step-by-step explanation:
Area for surface area of a rectangular prism:
\(A=2(wl+hl+hw)\)
Assuming:
\(l=10\\w=8\\h=3\)
\(A=2(80+30+24)= 268\)
Hope this helps!
Answer:
A
352
Step-by-step explanation:
What is the final amount if 392 is increased by 9% followed by a 3% decrease?
Give your answer rounded to 2 DP.
Answers
Answer:
392/100 X 109 = 427.28
427.28/100 X 97 = 414.4616
414.46
A car is traveling along a road that makes a 13° angle with the ground. Find the elevation of the car on a stretch of road that extends horizontally 125 meters. Round your answer to the nearest tenth.
Answers
Answer:
Therefore, the elevation of the car on the stretch of road, rounded to the nearest tenth, is approximately 29.7 meters.
Step-by-step explanation:
To find the elevation of the car on a stretch of road that extends horizontally 125 meters, we can use trigonometry.
Given:
Angle of the road = 13°
Horizontal distance = 125 meters
We can use the tangent function to calculate the elevation:
tan(angle) = opposite / adjacent
In this case, the opposite side represents the elevation, and the adjacent side represents the horizontal distance.
Let's denote the elevation as "e". The equation becomes:
tan(13°) = e / 125
To solve for "e", we can rearrange the equation:
e = 125 * tan(13°)
Using a calculator, we can evaluate this expression:
e ≈ 125 * tan(13°) ≈ 29.7
Help ASAP! Timed! State the domain and range of the graph in interval notation.

Answers
Answer:
Step-by-step explanation:

3x-6y=24 y=Mx+b form
Answers
Answer:
y=0.5x-4 or y=\(\frac{1}{2}\)x-4
Step-by-step explanation:
For this equation, it is mostly just rearranging variables.
We start with 3x-6y=24.
By subtracting 3x from both sides, you get -6y=-3x+24.
From there, dividing both sides by -6 leaves you with y=0.5x-4 aka y=\(\frac{1}{2}\)x-4 depending what format is asked.
** You may want to revise simplifying linear equations and algebraic equations. I'm always happy to help!
The 52 cards in a deck are numbered 1, 2,.......,52. Alex, Blair, Corey, and Dylan each picks a card from the deck without replacement and with each card being equally likely to be picked. The two persons with lower numbered cards form a team, and the two persons with higher numbered cards form another team. Let p(a) be the probability that Alex and Dylan are on the same team, given that Alex picks one of the cards a and a + 9, and Dylan picks the other of these two cards. The minimum value of p(a) for which p(a) > 1/2 can be written as m/n, where m and n are relatively prime positive integers. Find m + n.
Answers
The value of m + n comes out to be 37
In order to get p(a), Let's consider the probabilities of the events that Alex and Dylan can choose from the set {a, a + 9}, so there are 8 other cards that they can not pick. This can be written as:
P(Alex chooses a) = 2/50 = 1/25 as there are two cards in {a, a + 9}.
P(Dylan chooses a+9) = 2/49 (since there are now 49 cards left)
Conditional Probability
What is conditional probability? It is defined as the probability of how likely an event is supposed to happen given the probabilities of events before that.
Conditional Probability Formula
For our case, A is "Alex and Dylan in the same team," and B is "Alex chooses a and Dylan chooses a+9". Hence, we can write the required probability P(A|B) as:
P(A|B) = P(A and B) / P(B)
where P(A and B) = the probability that Alex and Dylan end up in the same team and Alex chooses a and Dylan chooses a+9.
P(B) = the probability that Alex chooses a and Dylan chooses a+9.
P(B) = P(Alex chooses a) * P(Dylan chooses a+9) = (1/25) * (2/49) = 2/1225
Now, let's find the probability of (A and B) i.e. the probability that Alex and Dylan end up in the same team and Alex chooses a and Dylan chooses a+9.
P(A and B) = P(Alex and Dylan end up in the same team and Alex chooses a and Dylan chooses a+9)
P(A and B) = P(Alex and Dylan end up in the same team and Alex and Dylan pick two cards less than or equal to a + 9) + P(Alex and Dylan end up in the same team and Alex and Dylan pick two cards greater than or equal to a + 10)
For Alex and Dylan to end up on the same team, Blair and Corey must pick two cards greater than a + 9.
Hence, the probability of this happening is the probability of Blair and Corey choosing two cards from the set {a + 10, a + 11, . . ., 52}, and this can be written as:
P(Blair and Corey pick 2 cards from the set {a + 10, a + 11, . . ., 52}) = [(52 - a - 9) C 2] / [(52 - a) C 2] = [(43 - a) C 2] / [(43 + a) C 2]
Now we need to find the minimum value of p(a) for which p(a) > 1/2 can be written as m/n, where m and n are relatively prime positive integers. Let's solve this part of the question. We will equate the above equation with 1/2 and solve for a.
In other words, we need to solve the following equation:
2[(a - 1) C 2 / (52 - a) C 2] + 2[(43 - a) C 2 / (43 + a) C 2] = 1
Here, we can use the factorials method to find the combination:
\({(a-1)\choose2} = \frac{(a-1)!}{2!(a-1-2)!}\)
which simplifies to
\(\frac{(a-1)(a-2)}{2!}\)
\({(52-a)\choose2} = \frac{(52-a)!}{2!(50-a)!}\)
which simplifies to
\(\frac{(52-a)(51-a)}{2!}\)
\({(43-a)\choose2} = \frac{(43-a)!}{2!(41-a)!}\)
which simplifies to
\(\frac{(43-a)(42-a)}{2!}\)
We get the equation:
\((a-1)(a-2)(43-a)(42-a) + (52-a)(51-a)(a-1)(a-2) = \frac{1}{2}*(52-a)(51-a)(43-a)(42-a)\)
= \((a-1)(a-2)[(43-a)(42-a) + (52-a)(51-a)] = \frac{1}{2}*(52-a)(51-a)(43-a)(42-a)\)
= \((a-1)(a-2)(a^2 - 95a + 2230) = \frac{1}{2}(a-10)(a-9)(a-44)(a-43)\)
Now we can see that for the minimum value of p(a) for which p(a) > 1/2 can be written as m/n, where m and n are relatively prime positive integers, we will have the value of p(a) just greater than 1/2 as that will give the minimum value that satisfies the condition.
Hence, we need to find the smallest value of a that satisfies this equation.
Now we can solve for a using the above equation. If we solve this equation, we get a = 19 or a = 35. We can then compute p(a) for both values of a using the formula we derived above. For a = 19, we get p(a) = 14/23, and for a = 35, we get p(a) = 13/23.
Hence, the minimum value of p(a) for which p(a) > 1/2 can be written as m/n, where m and n are relatively prime positive integers, is 14 + 23 = 14+23 = 37.
Learn more about conditional probability:
https://brainly.com/question/30144287
#SPJ11
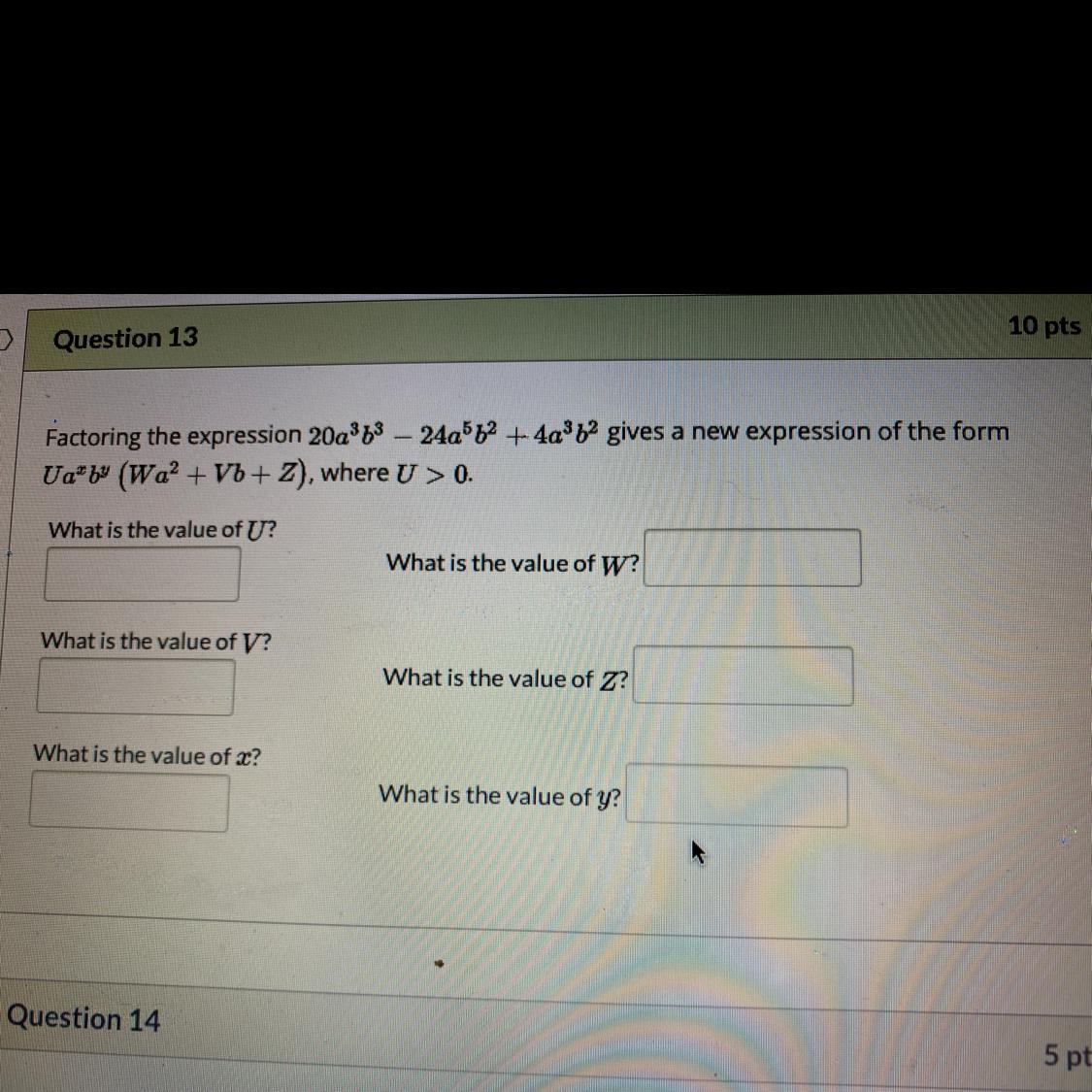
Factoring the expression 20a^3b^3 – 24a^5b^2 + 4a^3b^2 gives a new expression of the form
Ua^xb^y (Wa^2 + Vb+ z), where U > 0.
What is the value of U?
What is the value of W?
What is the value of V?
What is the value of Z?
What is the value of x?
What is the value of y?
Answers
Answer:
\(U = 4\\W = -6\\V = 5\\Z = 1\\x = 3\\y = 2\)
Step-by-step explanation:
Then given expression is:
\(20a^3b^3-24a^5b^2+4a^3b^2\)
To express the given expression in the form:
\(Ua^xb^y(Wa^2+Vb+Z)\)
and to find the values of \(U, W, V, Z, x, y\).
First of all, let us check the maximum common powers of \(a, b\) in each term from the given expression.
The maximum common power of \(a\) is 3 and
The maximum common power of \(b\) is 2.
So, we can take \(a^3b^2\) common out of each term.
And maximum common coefficient that can be taken out common is 4.
Taking 4\(a^3b^2\) common from each term of given expression, we get:
\(4a^3b^2(-6a^2+5b+1)\)
Now, let us compare the given term with:
\(4a^3b^2(-6a^2+5b+1)\) = \(Ua^xb^y(Wa^2+Vb+Z)\)
Now, the values that we get the following values:
\(U = 4\\W = -6\\V = 5\\Z = 1\\x = 3\\y = 2\)
which is our answer.
Which is the simplified form of the expression ((x^-3)(y^2)/(x4)(y^6))^3

Answers
Answer:
i think X^3y^12
Step-by-step explanation:
.......
The rates for a go-Kart course are shown.
NUMBER OF LAPS n | 1 | 2 | 3 | 4 | .
___________________________________
TOTAL COST ($) f(n) | 7 | 9 | 11 | 13 |
What is the total cost for the 15 laps?
Answers
Answer:
I am pretty late but eh
Step-by-step explanation:
1:7
2:9
3:11 and so on
proption 1:7 15:x
x=105
Does anyone know how to solve these types of triangles?

Answers
Answer:
x= 101
Step-by-step explanation:
Exterior angle of triangle states that the exterior angle of a triangle is the sum of the 2 opposite interior angles. This is abbreviated as 'ext. ∠ of ∆'. Thus using the exterior angle theorem,
x°= 64° +37° (ext. ∠ of ∆)
x°= 101°
x= 101
_____
Alternative method:
Let the third angle in the triangle be y°.
Since the sum of the angles in a triangle is 180°,
y° +64° +37°= 180° (∠ sum of ∆)
Simplify:
y° +101°= 180°
y°= 180° -101°
y°= 79°
The sum of the angles on a straight line is 180°.
x° +y°= 180° (adj. ∠s on a str. line)
Substitute y°= 79°:
x° +79°= 180°
x°= 180° -79°
x°= 101°
x= 101
In Mr. Senter's classroom, 2/3 of the students play sudoku. Of the students who play sudoku, 3/8 also play chess. If there are 24 students in his class, how many play sudoku and chess?
Answers
Answer:
9 students play sodoku and chess.
Step-by-step explanation:
What do we have?
2/3; play sudoku
3/8; play chess
24; students total
Find a common denominator for the fractions:
2/3x8/8
3/8x3/3
Now we have:
16/24
9/24
This also makes sense because we have a total of 24 students, now we want to know how many of them play sodoku AND chess; which was originally 3/8.
It's 9 students!
There are 16 students playing chess and 6 students playing sudoku.
What is the fraction?A fraction is defined as a numerical representation of a part of a whole that represents a rational number.
Given that 2/3 of the students play sudoku. of the students who play sudoku, 3/8 also play chess.
And there are 24 students in his class
First, we must determine how many students play chess, which is: In this scenario, we must multiply the total number of students by fractions to reach the answer.
⇒ 2/3×24 = 16
So 16 students are playing chess, and now, 3/8 of them are playing sudoku.
⇒ 3/8×16 = 6
Hence, there are 16 students playing chess and 6 students playing sudoku.
Learn more about the fraction here:
brainly.com/question/10354322
#SPJ2
which coordinate plane is closest to the point (8, 4, 6)? correct xz-plane yz-plane xy-plane correct: your answer is correct. find an equation of the sphere with center (8, 4, 6) that just touches (at one point) that coordinate plane.
Answers
The point t (8, 4, 6) in xyz plane is closest to xz plane.
What is a three-dimensional coordinate plane?In three-dimensional space, the Cartesian coordinate system is based on three mutually perpendicular coordinate axes,
the x-axis, the y-axis, and the z-axis.
Given, A point (8, 4, 6) in xyz plane.
We know in xz plane y is constant and similar for the other two xy and yz planes.
Now the point (8, 4, 6) is, 8 units on the x-coordinate, 4 units on the
y-coordinate, and 6 units on the z-coordinate.
Therefore, It is 4 units away from xz plane and it is the closest distance.
learn more about x-y-z coordinate here :
https://brainly.com/question/28563092
#SPJ1
The null hypothesis in an independent-samples t-test would be stated as which of the following:
Group of answer choices
a. The mean of the sample is not equal to the mean of the population.
b. The mean of sample 1 is not equal to the mean of sample 2.
c. The mean of sample 1 is equal to the mean of sample 2.
d. The mean of the sample is equal to the mean of the population.
Answers
The null hypothesis in an independent-samples t-test refers to the assumption that there is no significant difference between the means of two independent populations. In this context, "independent-samples" denotes that the two samples come from different populations and are not related. "Population" refers to the larger group from which the samples are taken.
Given the group of answer choices, the correct option for the null hypothesis in an independent-samples t-test is:
c. The mean of sample 1 is equal to the mean of sample 2.
This statement asserts that there is no significant difference between the means of the two samples. The null hypothesis serves as a starting point in the analysis, and the purpose of the t-test is to determine whether there is enough evidence to reject the null hypothesis in favor of an alternative hypothesis, which states that the means of the two samples are significantly different. The other answer choices do not accurately represent the null hypothesis for an independent-samples t-test.
Learn more about null hypothesis here: brainly.com/question/28920252
#SPJ11
Help please! I don't understand.

Answers
Answer:
Question 13: is Side-Side-Angel
Question 14: laws sines.
Question 15: is 1 (which b.)
there my brother tried his best, have a great day TwT
The Garcia family drives 3/4 of the distance to their. grandparents house in 3/4 hour. How many hours will it take to drive to their grandparents house at the same rate? A-9/16 B-1. C- 1 7/9
Answers
Answer:
B
Step-by-step explanation:
Finding Congruent Figures Two of these three triangles are congruent. Choose the triangle that is not congruent to the other two. A triangle has 1 side length of 2.8 centimeters and 2 side lengths of 2.6 centimeters. The angles opposite to sides with length of 2.6 centimeters are 58 degrees. The other angle is 64 degrees. A triangle has side lengths of 2.1 centimeters, 2.8 centimeters, and 2.6 centimeters. The angle opposite to side with length 2.1 centimeters is 45 degrees, opposite to side length of 2.6 centimeters is 62 degrees, and opposite to side length of 2.8 centimeters is 73 degrees. A triangle has side lengths of 2.1 centimeters, 2.8 centimeters, and 2.6 centimeters. The angle opposite to side with length 2.1 centimeters is 45 degrees, opposite to side length of 2.6 centimeters is 62 degrees, and opposite to side length of 2.8 centimeters is 73 degrees.
Answers
The lengths of the sides and the measure of the interior angles of the
three triangles determines which of the triangles are congruent.
Correct response;
The first triangle is not congruent to the other two trianglesWhich method is used to determine the triangles that are congruent?According to Side-Side-Side postulate, two triangles are congruent if
the lengths of the three sides of one triangle are equal to the lengths of
the three sides of the other triangle
The lengths of the sides of the second triangle are;
2.1 centimeters, 2.8 centimeters, and 2.6 centimetersThe side length of the third triangle are;
2.1 centimeters, 2.8 centimeters, and 2.6 centimetersTherefore; the second and the third triangles are congruent.
However, the side lengths of the first triangle are;
2.8 centimeters, 2.6 centimeters, and 2.6 centimetersGiven that the two of the sides of the first triangle are equal to 2.6
centimeters, while non of the sides of the second and third triangle are
equal, we have;
The first triangle is not congruent to the second and third triangles.Learn more about the rules of congruency here;
https://brainly.com/question/8531982
I am sorry, I am late but for future people here is the answer. :))

What series of transformations that maps one triangle onto the other. What does this tell us about the triangles

Answers
a group of 25 students spent 1,625 minutes studying for an upcoming test. what prediction can you make about the time it will take 130 students to study for the test?
Answers
Thus, it will take 130 students approximately 8,450 minutes to study for the test.
Based on the information provided, we can predict the time it will take for 130 students to study for the test. A group of 25 students spent 1,625 minutes studying. To find the average time per student, we divide the total time by the number of students:
Using unitary method:
1,625 minutes ÷ 25 students = 65 minutes per student
Now, we can use this average time to predict the time for 130 students:
65 minutes per student × 130 students = 8,450 minutes
Therefore, it will take 130 students approximately 8,450 minutes to study for the test.
Know more about the unitary method
https://brainly.com/question/23423168
#SPJ11
Please help, thank you
In a box are 6 purple and 4 pink socks. You randomly pick up two socks from the box. What is the probability that the socks have the same color? Answer with a quarrel in the simplest
Answers
Answer: Total number of socks = 6+4 = 10
There are 6 purple socks out of 10 total socks
as 6/10
There are now 9 socks total because he pulled one out, and 5 purple socks left because we assumed he pulled a purple sock out
So the next pull's is:
5/9
So the probability that he will pull two purple socks is:
(6/10)*(5/9) = 1/3 or 33.3% if you convert it to a percentage.
Step-by-step explanation:
Consider the ordered bases B = {1,x,x²} and C = {1, (2-1), (x - 1)²} for P2. (a) Find the transition matrix from C to B. ge 2 of 1 (b) Find the transition matrix from B to C. pages after page (c) Write p(x) = a + bx + cx² as a linear combination of the polynomials in C.
Answers
a) The transition matrix from C to B is [1 0 0], [0 1 0], [0 0 1] b) The transition matrix from C to B is [1 0 0], [0 1 0], [0 0 1] c) p(x) = a + bx + cx² as a linear combination of the polynomials in C can be defined as p(x) = a + b + c(x - 1)²
(a) Finding the transition matrix from C to B
To find the transition matrix from C to B, we need to express the vectors in the basis C as linear combinations of the vectors in basis B.
Let's express each vector in basis C in terms of basis B
1 = 1(1) + 0(x) + 0(x²)
(2 - 1) = 0(1) + 1(x) + 0(x²)
(x - 1)² = 0(1) + 0(x) + 1(x²)
The coefficients of the linear combinations are the entries of the transition matrix from C to B. Thus, the transition matrix is
[1 0 0]
[0 1 0]
[0 0 1]
(b) Finding the transition matrix from B to C:
To find the transition matrix from B to C, we need to express the vectors in the basis B as linear combinations of the vectors in basis C.
Let's express each vector in basis B in terms of basis C
1 = 1(1) + 0(2 - 1) + 0((x - 1)²)
x = 0(1) + 1(2 - 1) + 0((x - 1)²)
x² = 0(1) + 0(2 - 1) + 1((x - 1)²)
The coefficients of the linear combinations are the entries of the transition matrix from B to C. Thus, the transition matrix is
[1 0 0]
[0 1 0]
[0 0 1]
(c) Writing p(x) = a + bx + cx² as a linear combination of the polynomials in C
To write p(x) = a + bx + cx² as a linear combination of the polynomials in C, we need to express the polynomial p(x) in terms of the basis C.
We have the basis C = {1, (2 - 1), (x - 1)²}
p(x) = a + bx + cx² = a(1) + b(2 - 1) + c((x - 1)²) = a + b(2 - 1) + c((x - 1)²)
Thus, the polynomial p(x) = a + bx + cx² can be written as a linear combination of the polynomials in C as
p(x) = a + b(2 - 1) + c((x - 1)²)
Simplifying further
p(x) = a + b + c(x - 1)²
To know more about transition matrix here
https://brainly.com/question/30034998
#SPJ4
Madison took a taxi from her house to the airport. The taxi company charged a pick-up fee of $3.20 plus $5 per mile. The total fare was $98.20, not including the tip. Write and solve an equation which can be used to determine
m, the number of miles in the taxi ride.
Answers
Answer:
19 miles
Step-by-step explanation:
hope this helps!!

W= 4/p+2 solve for p
Answers
Answer:
(w-2)x4 = p (i think)
Step-by-step explanation:
A line segment has endpoints at (–4, –6) and (–6, 4). Which reflection will produce an image with endpoints at (4, –6) and (6, 4)? a reflection of the line segment across the x-axis a reflection of the line segment across the y-axis a reflection of the line segment across the line y = x a reflection of the line segment across the line y = –x
Answers
Answer:
reflection in the y- axis
Step-by-step explanation:
Under a reflection in the y- axis
a point (x, y ) → (- x, y )
Note the x- coordinate is opposite in sign and the y- coordinate remains unchanged.
Thus
(- 4, - 6 ) → (4, - 6 )
(- 6, 4 ) → (6, 4 )
The endpoints have been reflected in the y- axis
We want to see which reflection we need to use to transform the given segment into the desired one.
The correct answer is:
"a reflection of the line segment across the y-axis"
First, we want to change the segment with endpoints at (-4, -6) and (-6, 4) to a segment with endpoints (4, -6) and (6, 4).
Note that the only thing that changes is the x-value of the endpoints, so we need to apply a reflection that only changes the x-value.
That reflection is a reflection across the y-axis.
For a general point (x, y), a reflection across the y-axis transforms the point to (-x, y).
Then the correct option is:
"a reflection of the line segment across the y-axis"
If you want to learn more, you can read:
https://brainly.com/question/15476267
Which graph represents the function f(x)=2x/x²-1?
(TIMED)



Answers
Answer:
The graph in the bottom right corner.
Step-by-step explanation:
Answer: B. The second one. The one that has 3 lines on on the top right, one in the middle and one in the bottom left.
Step-by-step explanation:
Just graph it on a piece if paper like I did, you'll see
urn a contains six white balls and seven black balls. urn b contains five white balls and three black balls. a ball is drawn from urn a and then transferred to urn b. a ball is then drawn from urn b. what is the probability that the transferred ball was white given that the second ball drawn was white?
Answers
Using the Bayes' theorem, we find the probability that the transferred ball was white given that the second ball drawn was white to be 52/89, or approximately 0.5843.
To solve this problem, we can use Bayes' theorem, which relates the conditional probability of an event A given an event B to the conditional probability of event B given event A:
P(A|B) = P(B|A) * P(A) / P(B)
where P(A|B) is the probability of event A given that event B has occurred, P(B|A) is the probability of event B given that event A has occurred, P(A) is the prior probability of event A, and P(B) is the prior probability of event B.
In this problem, we want to find the probability that the transferred ball was white (event A) given that the second ball drawn was white (event B). We can calculate this probability as follows:
P(A|B) = P(B|A) * P(A) / P(B)
P(B|A) is the probability of drawing a white ball from urn b given that the transferred ball was white and is now in urn b. Since there are now six white balls and three black balls in urn b, the probability of drawing a white ball is 6/9 = 2/3.
P(A) is the prior probability of the transferred ball being white, which is the number of white balls in urn a divided by the total number of balls in urn a, or 6/13.
P(B) is the prior probability of drawing a white ball from urn b, which can be calculated using the law of total probability:
P(B) = P(B|A) * P(A) + P(B|not A) * P(not A)
where P(B|not A) is the probability of drawing a white ball from urn b given that the transferred ball was black and P(not A) is the probability that the transferred ball was black, which is 7/13.
To calculate P(B|not A), we need to first calculate the probability of the transferred ball being black and then the probability of drawing a white ball from urn b given that the transferred ball was black.
The probability of the transferred ball being black is 7/13. Once the transferred ball is moved to urn b, there are now five white balls and four black balls in urn b, so the probability of drawing a white ball from urn b given that the transferred ball was black is 5/9.
Therefore, we can calculate P(B) as follows:
P(B) = P(B|A) * P(A) + P(B|not A) * P(not A)
= (2/3) * (6/13) + (5/9) * (7/13)
= 89/117
Now we can plug in all the values into Bayes' theorem to find P(A|B):
P(A|B) = P(B|A) * P(A) / P(B)
= (2/3) * (6/13) / (89/117)
= 52/89
Therefore, the probability that the transferred ball was white given that the second ball drawn was white is 52/89, or approximately 0.5843.
To know more about Bayes' theorem refer here :
https://brainly.com/question/29598596#
#SPJ11
For each of the solutions of the equations find two consecutive integers between
which the solution is located :
x²=3
Answers
Answer:
0 and 1
Step-by-step explanation:
x² = 3
take the square root of both sides
x = {-√3, √3}
x ≈ {-1.73, 1.75}
Two consecutive integers between 1.73 and 1.75
0 and 1
A parking garage in charges a flat rate of $5.00 for 2 hours or less, and $0.25 per hour for each additional hour.
1. Write an equation to model this relationship.
2. How much do you have pay to park for 10 hours?
3. How many hours will $10 buy?
Answers
Answer:
Let's denote the total cost as C and the number of hours as h. The equation to model this relationship can be written as:
C = 5 + 0.25(h - 2)
The first part, 5, represents the flat rate for 2 hours or less. The second part, 0.25(h - 2), represents the additional hours beyond 2 hours, where each hour costs $0.25.
To calculate the cost of parking for 10 hours, we can substitute h = 10 into the equation:
C = 5 + 0.25(10 - 2)
C = 5 + 0.25(8)
C = 5 + 2
C = $7.00
Therefore, you would have to pay $7.00 to park for 10 hours.
To find out how many hours $10 will buy, we can set the equation equal to $10 and solve for h:
10 = 5 + 0.25(h - 2)
0.25(h - 2) = 10 - 5
0.25(h - 2) = 5
h - 2 = 5 / 0.25
h - 2 = 20
h = 20 + 2
h = 22
Therefore, $10 will buy you 22 hours of parking
find the square roots of 9604
Answers
Answer:
98
You have to use prime factor decompisition. I hope this helps
Answer:
it is either 98 or -98
Step-by-step explanation:
Given the number 9604
Taking the square root
=> \(\sqrt{9604}\)
=> ±98
So, it is either 98 or -98