Spend $1.85 & pay with a
$10.00 bill & you get $8.15 in
change. The digits in the
change are the same as the
digits in what you spent. Can
you find other amounts that
work this way?
Answers
Related Questions
Drag each term to the correct location on the expression. Each term can be used more than once, but not all terms will be used.
Completely factor this quadratic expression:
4x²2² +12x-72.
3
x² 2 4 4x 1 8
Reset
90
Next
+6)
Answers
The completely factored form of the quadratic expression 4x^2 + 12x - 72 is (x + 6) * 4(x - 3).
To completely factor the quadratic expression 4x^2 + 12x - 72, we can follow these steps:
Step 1: Find the product of the coefficient of the quadratic term (4) and the constant term (-72). In this case, the product is -288.
Step 2: Look for two numbers whose product is the same as the result obtained in Step 1 (-288) and whose sum is equal to the coefficient of the linear term (12). In this case, the numbers are 24 and -12.
Step 3: Rewrite the middle term (12x) using the two numbers found in Step 2:
4x^2 + 24x - 12x - 72
Step 4: Group the terms:
(4x^2 + 24x) - (12x + 72)
Step 5: Factor out the greatest common factor from each group:
4x(x + 6) - 12(x + 6)
Step 6: Notice that we have a common factor of (x + 6) in both terms. Factor it out:
(x + 6)(4x - 12)
Step 7: Simplify further by factoring out 4 from the second term:
(x + 6) * 4(x - 3)
The completely factored form of the quadratic expression 4x^2 + 12x - 72 is (x + 6) * 4(x - 3).
Simplify the equation (picture attatched)

Answers
Answer:
x°3 + x°2 + 4x - 48
( ° = it's the number at the top )
Please help, i dont quite understand this problem :(

Answers
6 sided shape=720
19. X and Y is 92
20.X and Y is 142
21. X and Y is 100.5
22.X and Y is 135
I believe this is correct
Find the inverse of the linear transformation y_1 = x_1 + 7x_2 y_2 = 3x_1 + 20x_2. In Exercises 9 through 12, decide whether the given matrix is invertible. Find the inverse if it exists. In Exercise 12, the constant k is arbitrary. [1 k 0 1] a. For which values of the constant k is the matrix [2 3 5 k] invertible? b. For which values of the constant k are all entries of [2 3 5 k]^-1 integers?
Answers
a) The matrix is invertible for all values of k except 7.5.
b) The only values of k that make all entries of [2 3 5 k]^-1 integers are 7 and 8.
To find the inverse of a linear transformation, we need to represent it in matrix form. The given linear transformation can be represented as a matrix:
[1 7]
[3 20]
To find the inverse of a matrix, we need to use the formula:
A^-1 = (1/det(A)) * adj(A)
Where det(A) is the determinant of the matrix A and adj(A) is the adjugate (transpose of the cofactor matrix) of A.
Using this formula, we can find the inverse of the given matrix as follows:
det([1 7][3 20]) = (1*20) - (7*3) = 1
adj([1 7][3 20]) = [20 -7][-3 1]
Therefore, the inverse of the matrix is:
[20 -7]
[-3 1]
To check that this is the correct inverse, we can verify that the product of the two matrices is the identity matrix:
[1 7][20 -7] = [1 0]
[3 20][-3 1] [0 1]
For exercise 9, we need to determine if the matrix [1 k 0 1] is invertible. To do this, we can find the determinant of the matrix:
det([1 k][0 1]) = (1*1) - (k*0) = 1
Since the determinant is not equal to zero, the matrix is invertible.
For exercise 12a, we need to find the values of k that make the matrix [2 3 5 k] invertible. To do this, we can again find the determinant of the matrix:
det([2 3][5 k]) = (2*k) - (3*5) = 2k - 15
For the matrix to be invertible, the determinant must be non-zero. Therefore, we need:
2k - 15 ≠ 0
2k ≠ 15
k ≠ 7.5
Therefore, the matrix is invertible for all values of k except 7.5.
For exercise 12b, we need to find the values of k that make all entries of [2 3 5 k]^-1 integers. To do this, we can find the inverse of the matrix:
[2 3][5 k]^-1 = (1/((2*k) - (3*5)))[k -3][-5 2]
We need all entries of this matrix to be integers. Therefore, we need:
1/((2*k) - (3*5)) to be an integer (i.e. the denominator is a factor of 1)
(k - 3)/((2*k) - (3*5)) and -5/((2*k) - (3*5)) to be integers
Simplifying the denominator, we get:
(2*k) - (3*5) = 2k - 15
Therefore, the denominator must be a factor of 1, which means it can only be 1 or -1.
If the denominator is 1, then:
2k - 15 = 1
2k = 16
k = 8
If the denominator is -1, then:
2k - 15 = -1
2k = 14
k = 7
Therefore, the only values of k that make all entries of [2 3 5 k]^-1 integers are 7 and 8.
To learn more about Matrix visit: brainly.com/question/12138961
#SPJ11
The owner of a small store buys coats for $40.00 each .she sells the coats for $7200 each. What percent of the purchase price is the sale price?
Answers
Use method of reduction of order to find a second solution y2(x) of the homogeneuos equation and a particular solution of the given nonhomogeneous equation:
y" - 4y = 2; y1 = e^-2x
Please use equation and not substitution
Answers
The homogeneous equation and a particular solution of the given nonhomogeneous equation is \(& y=c_1 e^{-2 x}+c_2 e^{2 x}-\frac{1}{2}\).
The given nonhomogeneous equation is y" - 4y = 2
We are given \($y_1=e^{-2 x}$\)
Let \($y_2=u y_1$\)
A linear differential equation is homogeneous if it is a homogeneous linear equation in the unknown function and its derivatives.Non-homogeneous differential equations are simply differential equations that do not satisfy the conditions for homogeneous equations. In the past, we’ve learned that homogeneous equations are equations that have zero on the right-hand side of the equation.
The two most common methods when finding the particular solution of a non-homogeneous differential equation are:
The method of undetermined coefficients. The method of variation of parameters.\($$\begin{aligned}& y_2=u e^{-2 x} \\& y_2^{\prime}=u^{\prime} e^{-2 x}-2 u e^{-2 x} \\& y_2^{\prime \prime}=u^{\prime \prime} e^{-2 x}-2 u^{\prime} e^{-2 x}-2 u^{\prime} e^{-2 x}+4 u e^{-2 x} \\& y_2^{\prime \prime}=u^{\prime \prime} e^{-2 x}-4 u^{\prime} e^{-2 x}+4 u e^{-2 x}\end{aligned}$$\)
Substitute in \($y^{\prime \prime}-4 y=0$\), we get
\($$\begin{aligned}& u^{\prime \prime} e^{-2 x}-4 u^{\prime} e^{-2 x}+4 u e^{-2 x}-4 u e^{-2 x}=0 \\& u^{\prime \prime} e^{-2 x}-4 u^{\prime} e^{-2 x}=0 \\& e^{-2 x}\left(u^{\prime \prime}-4 u^{\prime}\right)=0 \\& u^{\prime \prime}-4 u^{\prime}=0 \\& u^{\prime \prime}=4 u^{\prime}\end{aligned}$$\)
Substitute \($$u^{\prime}=v$ and $u^{\prime \prime}=v^{\prime}$\), we get
\($$\begin{aligned}& v^{\prime}=4 v \\& \frac{d v}{d x}=4 v \\& \frac{1}{v} d v=4 d x\end{aligned}$$\)
Integrate both sides, we get
\($u=\frac{1}{4} C_1 e^{4 x}+C_2$$\)
put in \($y_2=u y_1$\)
\($$y_2=\left(\frac{1}{4} C_1 e^{4 x}+C_2\right) e^{-2 x}$$\)
Choose \($$C_1=4$ and $C_2=0$\), we get
\($$y_2=e^{2 x}$$\)
\($$\begin{aligned}& y_c=c_1 y_1+c_2 y_2 \\& y_c=c_1 e^{-2 x}+c_2 e^{2 x}\end{aligned}$$\)
Particular Solution
\($$\begin{aligned}& y_y=A \\& y_y{ }^{\prime}=0 \\& y_y{ }^{\prime \prime}=0\end{aligned}$$\)
Substitute in \($y^{\prime \prime}-4 y=2$\), we get
\($$\begin{aligned}& 0-4 A=2 \\& -4 A=2 \\& A=-\frac{1}{2} \\& \therefore y_y=-\frac{1}{2}\end{aligned}$$\)
General Solution
\($$\begin{aligned}& y=y_6+y_y \\& y=c_1 e^{-2 x}+c_2 e^{2 x}-\frac{1}{2}\end{aligned}$$\)
Therefore, the second equation is \(& y_{2} =c_1 e^{-2 x}+c_2 e^{2 x}-\frac{1}{2}\).
For more such questions on homogeneous & nonhomogeneous equation
https://brainly.com/question/15839620
#SPJ4
Which is a simplified form of the expression -6a + 2(2a + 2)?
A.-2a + 4
B. -2a - 4
C. 2a + 4
D. 2a - 4
Answers
Answer:
-2a +4
Step-by-step explanation:
-6a + 2(2a + 2)
Distribute
-6a +4a +4
Combine like terms
-2a +4
Answer:
Answer A is correct
Step-by-step explanation:
First Solve the brackets
\( - 6a + 2(2a + 2) \\ - 6 a+ 4a + 4\)
Then combine like terms
\( - 6 a+ 4a + 4 \\ - 2 a + 4\)
The floor of a storage unit is 15 feet long and 8 feet wide. What is the distance between two opposite corners of the floor?
Answers
The distance between two opposite corners of the given floor is 17 feet.
What is Pythagoras's theorem?Pythagoras's theorem states that in a right-angled triangle, the square of one side is equal to the sum of the squares of the other two sides.
Given that the floor of a storage unit is 15 feet long and 8 feet wide.
Let x would be the distance between two opposite corners of the floor
As per the figure, We have a right triangle with legs 15 and 8 and with hypotenuse x.
According to Pythagoras's theorem,
x² = 15² + 8²
x² = 225 + 64
x² = 289
x = √289
x = 17
Thus, the distance is 17 feet between two opposite corners.
Learn more about Pythagoras's theorem here:
brainly.com/question/343682
#SPJ9

Find the value of X.
The chart is in the photo.

Answers
Answer:
x=8 bowls
Step-by-step explanation:
Answer:
8
Step-by-step explanation:
2K=14
K=7
7×8=56
this is the solution
In a Healthy Jogging event, a few hundred participants were expected to jog 7 800 000 metres altogether. They had jogged 25 000 metres in the first few minutes. How many thousands must be added to 25 000 to make 7 800 000?
Answers
we have to add 7775000 to make 7800000 from 25000 which is calculated by using Substraction method.
Subtraction in mathematics is the process of subtracting one integer from another. In other terms, the result of subtracting two from five is three. After addition, subtraction is usually the second process you learn in math class.Subtraction is the action or procedure of determining the difference between two quantities or figures. The phrase "taking away one number from another" is also used to describe the process of subtracting one number from another.
Distance to be covered altogether= 7800000 m
THE distance has covered= 25000 m.
We can calculate the thousands needs to be added in 25000 to make it 7800000 by using Substraction method:-
7800000-25000= 7775000m
hence, to make 7800000 from 25000 we have to add 7775000.
To know more about Substraction method go through:-
https://brainly.com/question/17301989
#SPJ4
I am not sure how to solve this. I have tried many times.

Answers
Answer:
,,,,,,,,,,,,,,,,,,,,,

Convert each measure to radians. 1. 225 2. 20 3.-255 4.-140" 5. 75 6.-300 Convert each measure to degrees. 7. 23x/128. -31x/369. x/1210. 5x/911.-x/-212. –7x/-613. 115014. 350015. -40016. -4600
Answers
The following can be answered by the concept of Trigonometry.
To convert degrees to radians, you need to use the formula:
radians = (degrees x pi)/180
1. 225 degrees = (225 x pi)/180 = (5/4)pi radians
2. 20 degrees = (20 x pi)/180 = (1/9)pi radians
3. -255 degrees = (-255 x pi)/180 = (-17/12)pi radians
4. -140 degrees = (-140 x pi)/180 = (-7/9)pi radians
5. 75 degrees = (75 x pi)/180 = (5/12)pi radians
6. -300 degrees = (-300 x pi)/180 = (-5/3)pi radians
To convert radians to degrees, you need to use the formula:
degrees = (radians x 180)/pi
7. 23x/128 radians = (23x/128 x 180)/pi degrees
8. -31x/369 radians = (-31x/369 x 180)/pi degrees
9. x/1210 radians = (x/1210 x 180)/pi degrees
10. 5x/911 radians = (5x/911 x 180)/pi degrees
11. -x/-212 radians = (-x/-212 x 180)/pi degrees
12. -7x/-613 radians = (-7x/-613 x 180)/pi degrees
13. 115014 radians = (115014 x 180)/pi degrees
14. 350015 radians = (350015 x 180)/pi degrees
15. -40016 radians = (-40016 x 180)/pi degrees
16. -4600 radians = (-4600 x 180)/pi degrees
To learn more about Trigonometry here:
brainly.com/question/15271751#
#SPJ11
Find the monthly house payment necessary to amortize the following loan. In order to purchase a home, a family borrows 335,000 at 2.375% for 30yc. What is their monthly payment?
Answers
The monthly payment necessary to amortize the loan is $1,306.09.
To calculate the monthly house payment necessary to amortize the loan, we need to use the loan amount, interest rate, and loan term.
Loan amount: $335,000
Interest rate: 2.375% per annum
Loan term: 30 years
First, we need to convert the annual interest rate to a monthly interest rate and the loan term to the number of monthly payments.
Monthly interest rate = Annual interest rate / 12 months
Monthly interest rate = 2.375% / 12 = 0.19792% or 0.0019792 (decimal)
Number of monthly payments = Loan term in years * 12 months
Number of monthly payments = 30 years * 12 = 360 months
Now we can use the formula for calculating the monthly payment on a fixed-rate mortgage, which is:
\(M = P * (r * (1+r)^n) / ((1+r)^n - 1)\)
Where:
M = Monthly payment
P = Loan amount
r = Monthly interest rate
n = Number of monthly payments
Substituting the given values into the formula:
\(M = 335,000 * (0.0019792 * (1+0.0019792)^{360}) / ((1+0.0019792)^{360} - 1)\)
Using this formula, the monthly payment comes out to approximately $1,306.09.
Therefore, the monthly payment necessary to amortize the loan is $1,306.09.
To learn more about annual interest rate visit:
brainly.com/question/22336059
#SPJ11
what is the square root of 45? What is the square root of 23? What is the square root of -23?
Answers
Answer:
square root of 45 is 6.71 when rounded up,
Step-by-step explanation:
square root of 45 is 6.7082093 we round up (numbers 5&up round up 4 and below go down) so we get 6.71
square root of 23 is 4.79583152 we round to 4.8
square root of -23 is 4.79583152 i . Yes,the i is part of the number.
Generally i means imaginary. also technically if this is for school they might accept this result as a negative number.
Hope this helps.
If the measure of arc WVX = 13x + 9 and m<WXZ = 5x + 36, find the m<WXY.
(Will give the correct answer the brainliest)
Answers
The measure of angle WXY can be found by setting up an equation using the given measures of arcs WVX and angles WXZ.
In a circle, the measure of an inscribed angle is equal to half the measure of its intercepted arc. We are given that the measure of arc WVX is 13x + 9 and the measure of angle WXZ is 5x + 36. To find the measure of angle WXY, we set up an equation:
m<WXY = 0.5 * (m<WVX)
Substituting the given values, we have:
m<WXY = 0.5 * (13x + 9)
Simplifying, we get:
m<WXY = 6.5x + 4.5
Therefore, the measure of angle WXY is represented by the expression 6.5x + 4.5, which depends on the value of x. Without additional information, we cannot determine the exact measure of angle WXY.
Learn more about Angles here: brainly.com/question/31818999
#SPJ11
Pls HELP I WILL MARK BRAINLIEST
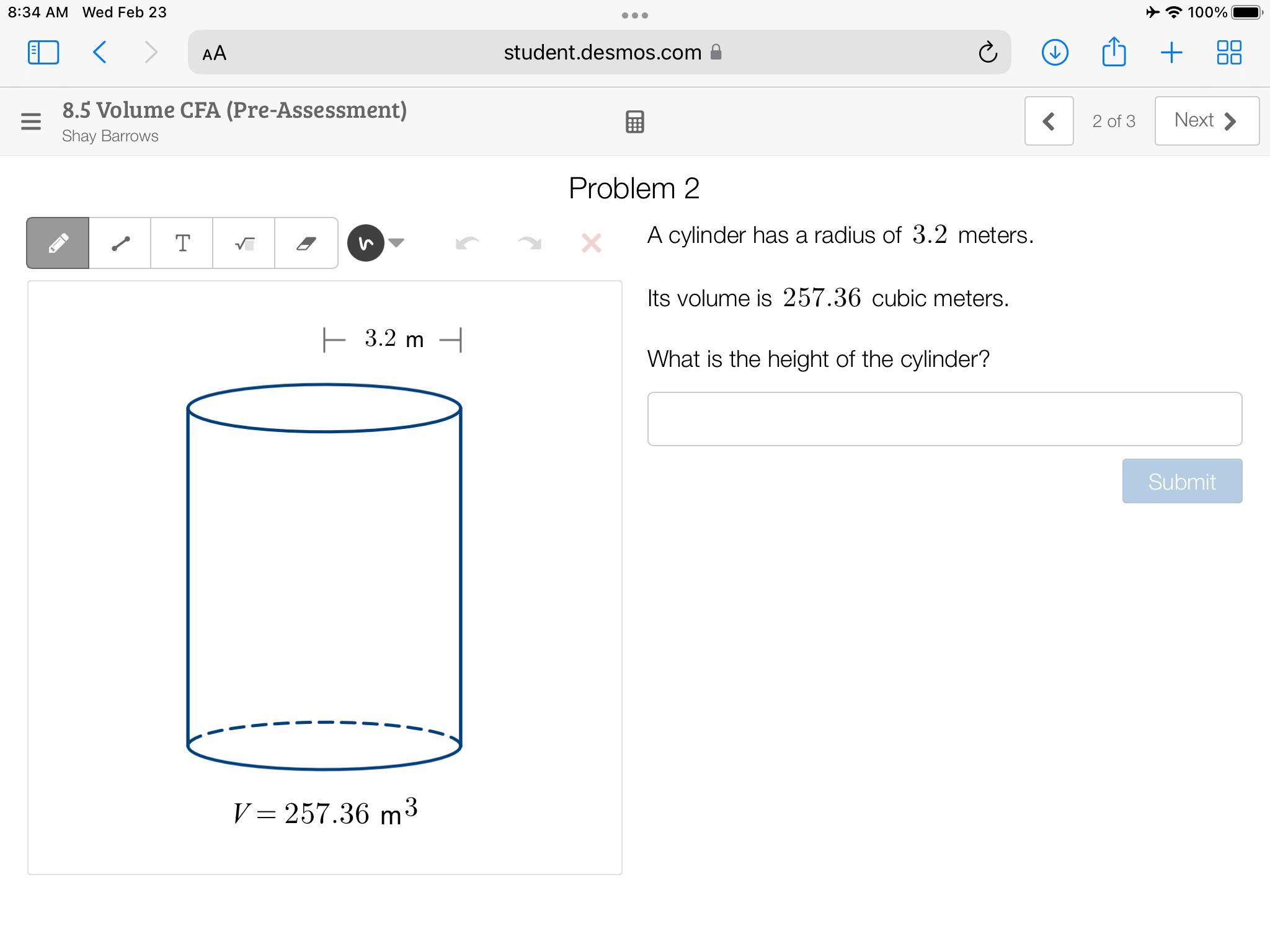
Answers
Answer:
h=8
Step-by-step explanation:
The height of the cylinder is approximately ≈ 8.00002
Or you can just put 8.
Step-by-step explanation:The reasoning for this is you can simply use the formula for a cylinder and just replace the variables.
h = V / π r²
Which then turns into
h = 257.36 / π 3.2²
and from there you get
≈ 8.00002
~Neo
if a sample of 7 keyboards is randomly selected, what is the probability that at least 6 of these will have a mechanical defect? (round your answer to four decimal places.)
Answers
The probability that at least 6 of the keyboards will have defects is 0.1429
These formal words are manipulated using logic and calculus rules, and any results are then comprehended or utilized in relation to the original problem domain. The study of patterns in biology and ecology, as well as financial analysis , can be done using probability.
Similar to finance, risk assessment can be used as a statistical technique to estimate the likelihood that unfavorable events will occur and can assist in putting processes in place to prevent encountering such circumstances. Probability is used to design games of chance so that owners may guarantee a profit while yet maintaining fairness.
A sample is picked. The sample contains 7 keyboards.
Now the probability that 6 of them are defective is 6/7
Now the probability that at least 6 are defective
= 1 -6/7
=0.14285...
≈ 0.1429
Like other theories, the theory of probability expresses its ideas using formal language or in terms that can be interpreted without regard to their meaning.
Hence the required probability is 0.1429
Learn more about probability visit:
brainly.com/question/24756209
#SPJ4
The point (−1,−√3) is given in Cartesian coordinates. A) Find the polar coordinates (r,θ) of the point, where r>0 and 0≤θ<2π. B) Find the polar coordinates (r,θ)
of the point, where r<0 and 0≤θ<2π.
Answers
For the given point (-1, -√3), we can only express its polar coordinates as (2, π/3), where r > 0 and 0 ≤ θ < 2π.
A) The polar coordinates (r, θ) of the point (-1, -√3) in Cartesian coordinates can be found using the formulas:
r = √(x^2 + y^2)
θ = arctan(y/x)
Substituting the given values, we have:
r = √((-1)^2 + (-√3)^2) = √(1 + 3) = 2
θ = arctan((-√3)/(-1)) = arctan(√3) = π/3
Therefore, the polar coordinates of the point (-1, -√3) are (2, π/3), where r > 0 and 0 ≤ θ < 2π.
B) If we consider r < 0, it means that the point lies in the opposite direction from the origin. However, in the polar coordinate system, r is always positive, so there are no polar coordinates for the point (-1, -√3) where r < 0. The polar coordinate system does not allow negative values for r.
To learn more about polar coordinates click here
brainly.com/question/31904915
#SPJ11
A coin weighs 7 ^-2 pounds. Find the either of 1000 of the coins. Round your answer to the nearest tenth.
Answers
Answer:
20.4 pounds
Step-by-step explanation:
Given that:
Weight of a coin = 7^-2 pounds
Weight of 1000 coins will be :
Weight per coin * number of coins
7^-2 * 1000
0.0204081 * 1000
= 20.408 pounds
= 20.4 pounds
PLEASE HELP WILL MARK BRAINEST!! THANK YOU!!

Answers
1) The polygons are not similar.
2) They polygons are similar.
3) They polygons are similar.
How to determine if the polygons are similar?Two polygons are similar if they have the same shape but different sizes. The corresponding angles are equal and the ratios of their corresponding sides are also equal.
Using the above concept, we can equate the ratio of the corresponding sides to see if the polygons are similar. That is:
No. 1
10/5 = 2
12/6 = 2
8/4.5 = 1.77
The ratios of the corresponding sides are equal. Thus, they are not similar.
No. 2
24/12 = 2
13.2/6.6 = 2
The ratios of the corresponding sides are equal. Thus, they are similar.
No. 3
22/5.5 = 4
26/6.5 = 4
12/3 = 4
The ratios of the corresponding sides are equal. Thus, they are similar.
Learn more about similar polygons on:
brainly.com/question/29492809
#SPJ1
36 divided by one-fifth equals what
Answers
Answer:
i looked it up and got 180/1 sorry if its not right
Step-by-step explanation:
Answer:180
Step-by-step explanation:
To divide by the fraction, multiply by the reciprocal of that fraction.
36 times 5 =180
180
if two events are independent, then their joint probability is computed with _________.
Answers
When two events are independent, their joint probability is computed by multiplying their individual probabilities.
When events are independent, it means that the occurrence of one event does not affect the probability of the other event happening. In such cases, the joint probability of both events occurring is calculated by multiplying their individual probabilities.
Let's consider two events, A and B, and assume they are independent. The probability of event A happening is denoted as P(A), and the probability of event B happening is denoted as P(B). To find the joint probability of both events occurring (P(A ∩ B)), we multiply their individual probabilities: P(A ∩ B) = P(A) * P(B).
This multiplication rule applies to any number of independent events. If there are more than two independent events, you would continue multiplying their individual probabilities to calculate the joint probability.
Note that this rule holds true only for independent events. If the events are dependent, the joint probability calculation becomes more complex and requires considering the conditional probability of one event given the occurrence of another event.
Learn more about multiply here: https://brainly.com/question/30875464
#SPJ11
10. Jacob ran at a rate of 7 miles per hour. At this rate, how far does he run in 30 minutes?
Answers
Answer: Jakob will run 3 1/2 miles in 30 min
Step-by-step explanation: you need to take 7 in half because half of an hpur is 30 minutes so half of seven is 3 1/2 so that is the answer
Answer:
3.5 miles
Step-by-step explanation:
1 hour = 60 minutes
Proportions:
7 miles = 60 minutes
J miles = 30 minutes
J = 7*30/60
J = 3.5 miles
NEED HELP IMMEDIATELY!
Simplify 10√2y + 5√2y + 3√2y.
A. 18√6y
B. 18√2y
C. 12√2y
D. 18√6y^3
(ANSWER IS NOT A)
Answers
18 root
2
Step-by-step explanation:
In this question imagine there is no y
It will be 10 root2 +5 root2 +3 root 2 it will be 18 root 2
Assume the weight of a randomly chosen American passenger car is a uniformly distributed random variable ranging from 2,180 pounds to 4,449 pounds.
[a] Mean weight of a randomly chosen vehicle
[b] Standard deviation of a randomly chosen vehicle
[c] Probability a vehicle will weigh less than 2,389 pounds
[d] Probability a vehicle will weigh more than 3,672 pounds
[e] Probability a vehicle will weigh between 2,389 and 3,672 pounds
Answers
The mean weight of a randomly chosen vehicle can be calculated by taking the average of the minimum and maximum weights:
Mean = (2,180 + 4,449) / 2 = 3,314.5 pounds
The standard deviation of a uniformly distributed random variable can be calculated using the following formula:
Standard Deviation = (Max - Min) / √12
Standard Deviation = (4,449 - 2,180) / √12 ≈ 652.48 pounds
To find the probability that a vehicle will weigh less than 2,389 pounds, we need to calculate the proportion of the total range that falls below 2,389 pounds:
Probability = (2,389 - 2,180) / (4,449 - 2,180) ≈ 0.317
To find the probability that a vehicle will weigh more than 3,672 pounds, we need to calculate the proportion of the total range that exceeds 3,672 pounds:
Probability = (4,449 - 3,672) / (4,449 - 2,180) ≈ 0.361
To find the probability that a vehicle will weigh between 2,389 and 3,672 pounds, we need to calculate the proportion of the total range that falls within this interval:
Probability = (3,672 - 2,389) / (4,449 - 2,180) ≈ 0.322
Know more about mean weight here:
https://brainly.com/question/16170417
#SPJ11
Malia is planting a garden in her yard.The dimensions are represented by x+4 feet and x+8 feet. She needs fencing to go around the perimeter of the garden to keep animals out. Which expression represents the amount of fencing she will need in feet. 4x+24 2x+12 (x+8)+(x+4) x^2+12
Answers
Answer:
I think you would have to do 2(x+4)+2(x+8) because it it talking about perimeter and if you imagine a square or rectangle, there are four sides, so just adding x+4 and x+8 wont be the whole perimeter. So, if you solve the expression 2(x+4)+2(x+8) it will give you 4x+24 XD
Step-by-step explanation:
a fair die is rolled times. find the probability that each of the final rolls is at least as large as the roll preceding it.
Answers
The probability that each of the final rolls is at least as large as the roll preceding it is \(1/6^6\) or 1/46656.
Given data,
A fair die is rolled n times. We have to find the probability that each of the final rolls is at least as large as the roll preceding it.The probability that each of the final rolls is at least as large as the roll preceding it means the probability of getting each number greater than the preceding one. So, there will be no duplicates.
First, find the total possible outcomes on a fair die. The total possible outcomes on a fair die are 6 because the numbers are 1,2,3,4,5,6. The number of possible outcomes for each roll of the die is 6. Then the total number of possible outcomes on the nth roll of a die is\(6^n\). There will be only one possible sequence in which each of the final rolls is at least as large as the roll preceding it. Let's check it from the following table.
Roller 1Roller 2Roller 3Roller 4Roller 5Roller 61-2-3-4-5-6
Here, we got only one sequence 1,2,3,4,5,6 to have each number greater than the preceding one. So, the probability of getting this sequence is \(1/6^6\).
for such more question on probability
https://brainly.com/question/24756209
#SPJ11
Suppose that for cast-iron pipe of a particular length, the expected number of failures is 1 (very close to one of the cases considered in the article). Then X, the number of failures, has a Poisson distribution with m 5 1.
Answers
P(X ≤ 4) by using the Cumulative Poisson Probabilities table in : P(X ≤ 4) = 0.785.
In this problem, we are given that the number of failures X in a cast-iron pipe of a particular length follows a Poisson distribution with an expected value (mean) of μ = 1.
To find P(X ≤ 4), we need to calculate the cumulative probability up to 4, which includes the probabilities of 0, 1, 2, 3, and 4 failures. We can use the Cumulative Poisson Probabilities table in the Appendix of Tables to find the cumulative probabilities.
From the table, we can look up the values for each number of failures and add them up to find P(X ≤ 4).
The cumulative probabilities for each value of k are:
P(X = 0) = 0.367
P(X = 1) = 0.736
P(X = 2) = 0.919
P(X = 3) = 0.981
P(X = 4) = 0.996
P(X ≤ 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) = 0.367 + 0.736 + 0.919 + 0.981 + 0.996 = 0.785
Therefore, P(X ≤ 4) is approximately 0.785 (rounded to three decimal places).
To know more about Poisson Probabilities, refer here:
https://brainly.com/question/33000341#
#SPJ11
Complete question
The article "Expectation Analysis of the Probability of Failure for Water Supply Pipes"† proposed using the Poisson distribution to model the number of failures in pipelines of various types. Suppose that for cast-iron pipe of a particular length, the expected number of failures is 1 (very close to one of the cases considered in the article). Then X, the number of failures, has a Poisson distribution with μ = 1. (Round your answers to three decimal places.)
(a) Obtain P(X ≤ 4) by using the Cumulative Poisson Probabilities table in the Appendix of Tables. P(X ≤ 4) =
Is 2/6 greater than 2/4?
Answers
Answer:
no
Step-by-step explanation:
2/6 simplifies to 1/3 and 2/4 simplifies to 1/3. 1/2 is greater than 1/3
x − 3y if x = 3 and y = −2.
Answers
Answer:
Step-by-step explanation:
x - 3y
3 - 3(-2) = 3 + 6 = 9