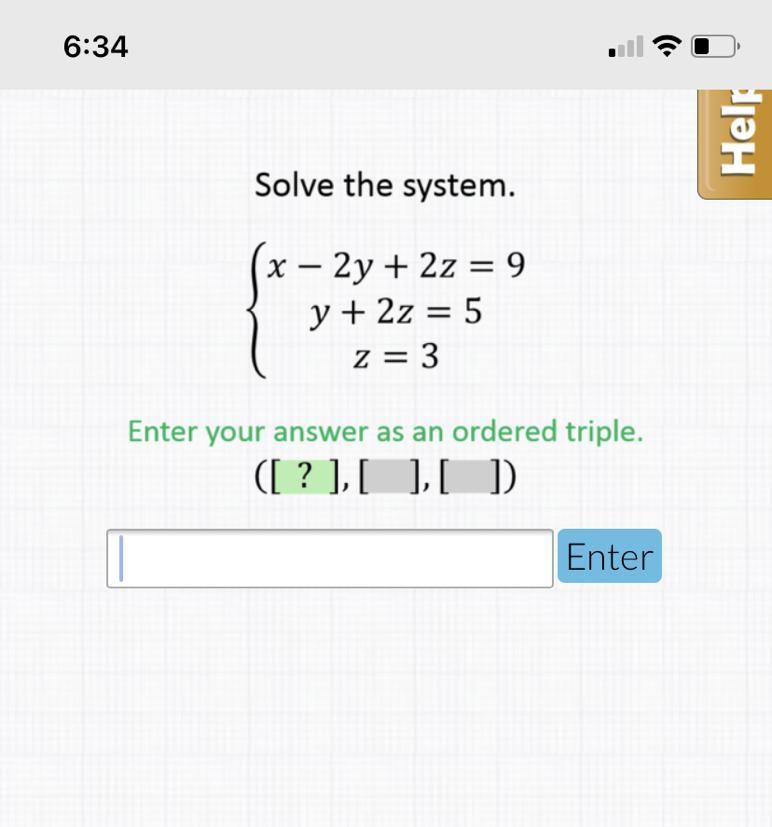
Answers
Answer:
x = 1, y = -1, z = 3
Step-by-step explanation:
x - 2y + 2z = 9
y + 2z = 5
z = 3
According to the last equation, z is equal to 3 so we can plug that in and our new 2 equations will be:
x - 2y + 6 = 9
y + 6 = 5
We can subtract 6 from both sides of the second equation to end up with:
y = -1
Now plugging this into the first equation, we have:
x + 2 + 6 = 9
x + 8 = 9
Subtract 8 from both sides
x = 1
Related Questions
What happens if you can write a function as a composite in different ways? Do you get the same derivative each time? The Chain Rule says you should. Find
dy/dx if y=x by using the Chain Rule with y as a composite of the following functions. Complete parts (a) and (b) below.

Answers
Using the Chain Rule, we have: dy/dx = f'(g(x)) * g'(x) = 1 * 1 = 1.The derivative of y with respect to x is 1.
When we compose a function, it may be possible to write it in a variety of different ways. Differentiating such functions can result in different derivatives, but the Chain Rule indicates that the derivatives of the compositions should be the same regardless of how the function is written, if the function is continuous and differentiable.For instance, consider the function f(x) = sin(x²). It can be written as f(g(x)) where g(x) = x² and f(x) = sin(x). Furthermore, it can be written as f(h(x)) where h(x) = x² and f(x) = sin(x). These are both compositions of functions, but they are different compositions that lead to different derivatives.However, if the function is a composite of differentiable functions, the Chain Rule tells us that the derivative of a composite function is the derivative of the outer function multiplied by the derivative of the inner function.
To find dy/dx if y = x using the Chain Rule with y as a composite of the following functions, we must first rewrite y as a composite function: y = f(g(x)) where g(x) = x and f(x) = x. This composite function can be written in a variety of different ways, such as y = f(h(x)) where h(x) = x and f(x) = x, or y = f(k(x)) where k(x) = x and f(x) = x. However, regardless of how we write it, the Chain Rule tells us that the derivative of y is equal to the derivative of the outer function (f(x) = x) multiplied by the derivative of the inner function (g(x) = x).
For more such questions on derivative
https://brainly.com/question/26369159
#SPJ8
Which statements are correct? Select all that apply.
Expanding is the same as using the distributive property.
Factoring means going from ab + ac to a(b + c).
Factoring can only be done when an expression has two terms.
Factoring can only be done when an expression has plus signs.
Answers
Statement 1, 2 and 3 are correct about using the distributive property.
Expanding is the same as using the distributive property. Factoring means going from ab + ac to a(b + c).Factoring can only be done when an expression has two terms.
Statement 1: Expanding is the same as using the distributive property. The distributive property states that a(b + c) = ab + ac. When we expand an expression, we are multiplying everything out. So, expanding an expression is the same as using the distributive property. Therefore, this statement is correct.
Statement 2: Factoring means going from ab + ac to a(b + c).When we factor an expression, we are essentially undoing the distributive property. In other words, we are going from a common factor in the two terms to a product. This is exactly what happens when we factor ab + ac to a(b + c). Therefore, this statement is correct.
Statement 3: Factoring can only be done when an expression has two terms. Factoring is the process of breaking down an expression into simpler factors. However, in order to do that, the expression needs to have two or more terms. If the expression only has one term, then we cannot factor it. Therefore, this statement is correct.
Statement 4: Factoring can only be done when an expression has plus signs. This statement is incorrect. Factoring can be done when an expression has either plus signs or minus signs. For example, we can factor x² - 4 to (x + 2)(x - 2). Therefore, this statement is incorrect.
For more such questions on distributive property , Visit:
https://brainly.com/question/2807928
#SPJ8
Suppose that 45% of students in a college have a smart phone. If you select three students at random, what is the probability that all three have a smart phone? Give your answer as a decimal (to at least 3 places) or fraction
Answers
Answer:
\( P(X=3)\)
And we can use the probability mass function and we got:
\(P(X=3)=(3C3)(0.45)^3 (1-0.45)^{3-3}=0.091\)
Then the probability that all three have a smart phone is 0.091
Step-by-step explanation:
Let X the random variable of interest "number of students with smartphone", on this case we now that:
\(X \sim Binom(n=3, p=0452)\)
The probability mass function for the Binomial distribution is given as:
\(P(X)=(nCx)(p)^x (1-p)^{n-x}\)
Where (nCx) means combinatory and it's given by this formula:
\(nCx=\frac{n!}{(n-x)! x!}\)
And we want to find this probability:
\( P(X=3)\)
And we can use the probability mass function and we got:
\(P(X=3)=(3C3)(0.45)^3 (1-0.45)^{3-3}=0.091\)
Then the probability that all three have a smart phone is 0.091
please solve for both parts

Answers
(a) The differential equation
\(y' + \dfrac14 y = 3 + 2 \cos(2x)\)
is linear, so we can use the integrating factor method. We have I.F.
\(\mu = \displaystyle \exp\left(\int \frac{dx}4\right) = e^{x/4}\)
so that multiplying both sides by \(\mu\) gives
\(e^{x/4} y' + \dfrac14 e^{x/4} y = 3e^{x/4} + 2 e^{x/4} \cos(2x)\)
\(\left(e^{x/4} y\right)' = 3e^{x/4} + 2 e^{x/4} \cos(2x)\)
Integrate both sides. (Integrate by parts twice on the right side; I'll omit the details.)
\(e^{x/4} y = 12 e^{x/4} + \dfrac8{65} e^{x/4} (8\sin(2x) + \cos(2x)) + C\)
Solve for \(y\).
\(y = 12 + \dfrac8{65} (\sin(2x) + \cos(2x)) + Ce^{-x/4}\)
Given that \(y(0)=0\), we find
\(0 = 12 + \dfrac8{65} (\sin(0) + \cos(0)) + Ce^0 \implies C = -\dfrac{788}{65}\)
and the particular solution to the initial value problem is
\(\boxed{y = 12 + \dfrac8{65} (\sin(2x) + \cos(2x)) - \dfrac{788}{65} e^{-x/4}}\)
As \(x\) gets large, the exponential term will converge to 0. We have
\(\sin(2x) + \cos(2x) = \sqrt2 \sin\left(2x + \dfrac\pi4\right)\)
which means the trigonometric terms will oscillate between \(\pm\sqrt2\). So overall, the solution will oscillate between \(12\pm\sqrt2\) for large \(x\).
(b) We want the smallest \(x\) such that \(y=12\), i.e.
\(0 = \dfrac8{65} (\sin(2x) + \cos(2x)) - \dfrac{788}{65} e^{-x/4}\)
\(\dfrac{788}{65} e^{-x/4} = \dfrac{8\sqrt2}{65} \sin\left(2x + \dfrac\pi4\right)\)
\(\dfrac{197}{\sqrt2} e^{-x/4} = \sin\left(2x + \dfrac\pi4\right)\)
Using a calculator, the smallest solution seems to be around \(\boxed{x\approx21.909}\)
it is the rate of change in angle measure of a unit of time
Answers
Answer:
j
Step-by-step explanation:
j
please help i will give brainliest

Answers
Answer:
1 5/12
Step-by-step explanation:
You can do the opposite of this problem to get the answer. 2/3 + 3/4 = 1 5/12. You can confirm this answer by doing 1 5/12 - 3/4. Therefore, 1 5/12 is your answer.
The governor of state A earns $54,900 more than the governor of state B. If the total of their salaries is $310,850, find the salaries of each.
need to find a and b
Answers
Answer:
$127975, $182875
Step-by-step explanation:
Let the salary in state A be x. Then, the salary in state B is x+54900.
\(x+x+54900=310850 \\ \\ 2x=255950 \\ \\ x=127975 \\ \\ x+54900=182875\)
What is the midpoint between (8,-5) and (2,-2)?
O (3,-1.5)
O (10,-7)
O (5, -1.5)
O (5,-3.5)

Answers
Answer:
O (5,-3.5)
Step-by-step explanation:
The volume of a rectangular prism is 5,890.625 cm3. If the height is 14.5 cm and the length is 25 cm, what is the value of the width?
Answers
Answer:
Step-by-step explanation:
The formula for the volume of a rectangular prism is V = lwh, where V is the volume, l is the length, w is the width, and h is the height.
We know that V = 5,890.625 cm^3, h = 14.5 cm, and l = 25 cm.
Substituting these values into the formula, we get:
5,890.625 = 25w(14.5)
5,890.625 = 362.5w
w = 16.25
Therefore, the width of the rectangular prism is 16.25 cm.
Answer:
It's A
Step-by-step explanation:
well all you have to do is divide like 5,890.625 dvided by 14.5 then divide again by 25 them bam you got 16.25
As an introduction to probability, a student asked to roll a fair, six sided number cube seven times the results of those seven rolls are shown below 1,4,4,4,4,6,5 what is the standard deviation of the data?
Answers
Using it's concept, the standard deviation of the data is of 3.742.
What are the mean and the standard deviation of a data-set?The mean of a data-set is given by the sum of all values in the data-set, divided by the number of values.The standard deviation of a data-set is given by the square root of the sum of the differences squared between each observation and the mean, divided by the number of values.For this data-set, the mean is:
M = (1 + 4 + 4 + 4 + 4 + 6 + 5)/7 = 4.
Hence the standard deviation is:
\(S = \sqrt{\frac{(1 - 4)^2 + (4 - 4)^2 + (4 - 4)^2 + (4 - 4)^2 + (4 - 4)^2 + (6 - 4)^2 + (5 - 4)^2}{7}} = 3.742\)
More can be learned about the standard deviation of a data-set at brainly.com/question/12180602
#SPJ1
The area of a rectangle is 48 m^2 the length is (x+2) and width is (x). What is the value of x?
Answers
Answer:
Please find attached pdf
Step-by-step explanation:
EMERGENCY PLEASE HELP
A company deposits $5,000 in a bank account that earns 3%
compound interest each year. Which function represents the value,
V(t), in dollars, of the bank account after t years?
Answers
Answer:
5150
Step-by-step explanation:
Answer: v(t) = 5,000(1.03)t
Step-by-step explanation:
A rectangular room is
4
times as long as it is wide, and its perimeter is
50
meters. Find the dimension of the room.
Answers
The width of the room is 5 meters and its length is 20 meters.
What is the formula for the Perimeter of Rectangle?A rectangle is a plane figure with four straight sides and four right angles, especially one with unequal adjacent sides, in contrast to a square.
The Perimeter of rectangle is -
P = 2(x + y)
The Area of rectangle is -
A = xy
We can write -
P = 2x + 2y
Py = 2xy + 2y²
Py = 2A + 2y²
2y² - Py + 2A = 0
y = ± (P² - 16A)/4
Given is a rectangular room is 4 times as long as it is wide. Its perimeter is 50.
Perimeter of the room -
2(x + y) = 50
and
x = 4y
Then, the perimeter of the room -
2(x + y) = 50
2(5y) = 50
5y = 25
y = 5 m
Then -
x = 20 m
Hence, the width of the room is 5 meters and its length is 20 meters.
To solve more questions on Rectangles and their Dimensions, visit the link below -
brainly.com/question/26183930
#SPJ1
An arrow is shot from 3 ft above the top of a hill with a vertical upward velocity of 108 ft/s. If it strikes the plain below after 9.5 s, how high is the hill?
If the arrow is launched at t0, then write an equation describing velocity as a function of time?
Answers
The height of the hill is approximately 25.73 ft. Where v0 is the initial velocity (108 ft/s), g is the acceleration due to gravity \((-32.2 ft/s^2)\),
To find the height of the hill, we can use the formula for the vertical position of an object under constant acceleration:
h = h0 + v0t + 1/2at^2
where h is the final height, h0 is the initial height, v0 is the initial velocity, t is the time, and a is the acceleration due to gravity (-32.2 ft/s^2).
In this case, we are given that the initial height h0 is 3 ft, the initial velocity v0 is 108 ft/s, and the time t is 9.5 s. We want to find the height of the hill, which we can denote as h_hill. The final height is the height of the plain, which we can denote as h_plain and assume is zero.
At the highest point of its trajectory, the arrow will have zero vertical velocity, since it will have stopped rising and just started to fall. So we can set the velocity to zero and solve for the time it takes for that to occur. Using the formula for velocity under constant acceleration:
v = v0 + at
we can solve for t when v = 0, h0 = 3 ft, v0 = 108 ft/s, and a = -32.2 ft/s^2:
0 = 108 - 32.2t
t = 108/32.2 ≈ 3.35 s
Thus, it takes the arrow approximately 3.35 s to reach the top of its trajectory.
Using the formula for the height of an object at a given time, we can find the height of the hill by subtracting the height of the arrow at the top of its trajectory from the initial height:
h_hill = h0 + v0t + 1/2at^2 - h_top
where h_top is the height of the arrow at the top of its trajectory. We can find h_top using the formula for the height of an object at the maximum height of its trajectory:
h_top = h0 + v0^2/2a
Plugging in the given values, we get:
h_top = 3 + (108^2)/(2*(-32.2)) ≈ 196.78 ft
Plugging this into the first equation, we get:
h_hill = 3 + 108(3.35) + 1/2(-32.2)(3.35)^2 - 196.78
h_hill ≈ 25.73 ft
If the arrow is launched at t0, the equation describing velocity as a function of time would be:
v(t) = v0 - gt
For such more questions on velocity
https://brainly.com/question/25749514
#SPJ8
Which number is closest to zero on the number line?

Answers
Answer:
the answer is .5 I think I'm sorry if I'm wrong
Six plus five times a number is more than the
number plus eight. Write an inequality and
solve it.
Answers
Answer:
x > 0.5
Step-by-step explanation:
Let the number be x.
6 + 5x > x + 8
4x > 2
x > 0.5
This is a question on inequalities. If you wish to venture further into it/understand this topic better, you may want to follow my Instagram account (learntionary), where I post some of my own notes on certain topics and also some tips that may be useful to you :)
Put these numbers in order from least to greatest.
-5
14
20
12
15
10
25
Submit
Answers
Answer:
-5, 10, 12, 14, 15, 20, 25
Suppose a population grows according to the logistic equation but is subject to a constant total harvest rate of H. If N(t) is the population size at time t, the population dynamics are dN dt = r 1 − N K N − H. Different values of H will result in different equilibrium population sizes, and if H is large enough we might expect extinction.(a) Suppose r = 2, K = 1000, and H = 100. Find all equilibria. (Round your answers to the nearest integer. Enter your answers as a comma-separated list.) N hat =(b) Determine whether each of the equilibria found in part is locally stable or unstable. (Round your answers to the nearest whole number. Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.) stable N hat = unstable N hat =Is the population predicted to go extinct?YesNo
Answers
Answer:
a) Equilibrium point : [ 947, 53 ]
b) N = 947 is stable equilibrium, N = 53 is unstable equilibrium
c) N0, the population will not go extinct
Step-by-step explanation:
a)
Given that;
r = 2, k = 1000, H = 100
dN/dT = R(1 - N/k)N - H
so we substitute
dN/dt = 2( 1 - N/1000)N - 100
now for equilibrium solution, dN/dt = 0
so
2( 1 - N/1000)N - 100 = 0
((1000 - N)/1000)N = 50
N^2 - 1000N + 50000 = 0
N = 1000 ± √(-1000)² - 4(1)(50000)) / 2(1)
N = 947.213 OR 52.786
approximately
N = 947 OR 53
Therefore Equilibrium point : [ 947, 53 ]
b)
g(N) = 2( 1 - N/1000)N - 100
= 2N - N²/500 - 100
g'(N) = 2 - N/250
SO AT 947
g'(N) = g'(947) = 2 - 947/250 = -1.788 which is less than (<) 0
so N = 947 is stable equilibrium
now AT 53
g'(N) = g"(53) = 2 - 53/250 = 1.788 which is greater than (>) 0
so N = 53 is unstable equilibrium
The capacity k=1000
If the population is less than 53 then the population will become extinct but since the capacity is equal to 1000 then the population will not go extinct.
Find the area of the square whose side length is 5s.
Answers
ANSWER
25s²
EXPLANATION
The area of a square with side length a is the square of its side length:
PLEASE HELP!!!!! MIDDLE SCHOOL MATH!!!!!!!!!!!!
Use the figure shown. Match each angle to the correct angle measure. Some angle measures may be used more than once or not at all.
PLEASE LOOK AT THE PICTURE BELOW!!!!! SHOW WORK!!!!!!!!

Answers
The values of all angles \( \angle \: GAL, \angle \: LAO, \angle CAO, \: angle \: KAC\) are 71°, 90°, 90°, 90° respectively.
Given angle GAK is 19°.
It is clear that angle KAL is equal to 90°.
So,
\( \angle KAL = {90}^{o} \)
Now,
\( \angle \: KAL = \angle KAG+ \angle \: GAL\)
So,
\( \angle \: GAL = {90}^{o} - {19}^{o} \\ = {71}^{o} \)
Now,
\( \angle \: KAO = 180°\)
Now
\( \angle \: KAL + \angle \: LAO = {180}^{o} \\ \angle \: LAO = {180}^{o} - {90}^{o} \\ \angle \: LAO = {90}^{o} \)
Again,
\( \angle \: CAO = {180}^{o} - \angle \: LAO \\ \angle \: CAO = {180}^{o} - {90}^{o} = {90}^{o} \)
Similarly,
\( \angle \: KAC = \angle \: KAO - \angle \: CAO \\ \angle \: KAC = {180}^{o} - {90}^{o} \\ = {90}^{o} \)
Learn more about angles:
https://brainly.com/question/30147425
#SPJ1
Solve the two simultaneous equations.
You must show all your working.
3t+2p=15.5
5t+4p=28.5
Answers
Answer:
Given equations are,
5x+2y=−2 (1)
3x−5y=17.4 (2)
Multiply equation (1) by 5 and equation (2) by 2, we get,
5(5x+2y)=5×−2
∴25x+10y=−10 (3)
2(3x−5y)=2×17.4
∴6x−10y=34.8 (4)
Adding equations (3) and (4), we get,
31x=24.8
∴x=
31
24.8
Put this value in equation (1), we get,
5(
31
24.8
)+2y=−2
∴
31
124
+2y=−2
∴2y=−2−
31
124
∴2y=
31
−186
∴y=
31
−93
Step-by-step explanation:
In the diagram below, AD EB, m/ABD = 115° and m/D = 27°.
Find m < ABE

Answers
The value of angle ABE is 52°
What are interior angle of a triangle ?A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted by triangle ABC.
The interior angles of a triangle are the inside angles formed where two sides of the triangle meet.
The sum of interior angle in a triangle is 180°
Angle EBD = 180-(90+27)
= 180-117
= 63°
angle ABE + EBD = ABD
ABE = ABD - EBD
ABE = 115-63
= 52°
Therefore the value of angle ABE is 52°
learn more about interior angle of triangle from
https://brainly.com/question/25215131
#SPJ1
b) 8xy +4y² factorise
Answers
Answer:
The answer is: 4y(2x+y)
Step-by-step explanation:
How do I find x? It’s for a riddle

Answers
Answer:
106
Step-by-step explanation:
174-68=106
Nathaniel would like to establish a trust fund that will provide R380 000 a year, forever, for his descendants. The trust fund will be invested very conservatively, so the expected rate of return is only 6,45%. How much money must he deposit today, to fund this gift for his descendants?
Answers
Answer:
Step-by-step explanation:
To calculate the amount of money Nathaniel needs to deposit today to fund this gift for his descendants, we can use the present value formula for a perpetuity:
Present Value = Annual Payment / Discount Rate
In this case, the annual payment is R380 000 and the discount rate (expected rate of return) is 6.45% in decimals, or 0.0645 as a fraction. So we can plug these values into the formula:
Present Value = R380 000 / 0.0645
This gives us a present value of approximately R5,899,225.68. Therefore, Nathaniel would need to deposit R5,899,225.68 today into the trust fund to provide R380 000 a year forever for his descendants, assuming a 6.45% expected rate of return.
What effect will replacing x with (x - 4)have on the
graph of the equation y = (x - 3)²?
A. slides the graph 4 units up
B. slides the graph 7 units down
OC. slides the graph 4 units right
D. slides the graph 1 unit right
Answers
Answer: D. slides the graph 1 unit right
Step-by-step explanation:
See attached image.

The question is asked in the attached file,. Kindly someone answer it in the best way.

Answers
According to the Empirical Rule, 99.7% of the measures fall within 3 standard deviations of the mean in the normal distribution.
What does the Empirical Rule state?The Empirical Rule states that, for a normally distributed random variable, the symmetric distribution of scores is presented as follows:
The percentage of scores within one standard deviation of the mean of the distribution is of approximately 68%.The percentage of scores within two standard deviations of the mean of the distribution is of approximately 95%.The percentage of scores within three standard deviations of the mean off the distribution is of approximately 99.7%.More can be learned about the Empirical Rule at https://brainly.com/question/10093236
#SPJ1
Which expression is equivalent to 2.8×107+2.7×106?
A
5.5×1015
B
5.5×107
C
3.07×107
D
7.56×106
Answers
Answer:
B or D
Step-by-step explanation:
I would go with D
Solve the equation x-4/2=10
Answers
x+-2=10
x-2=10
x-2+2=10+2
x=12
Answer:
x=12
Step-by-step explanation:
x-4/2=10
x-2=10
+2. +2
x=12
Please help me answer this with the correct answer :)
Explain your answer
I will give braisnlt :)
Answers
Answer:
Hey
Step-by-step explanation:
Where is the question