Simplify as far as possible.
2√125−5√5
Answers
Answer:
5
Step-by-step explanation:
Simplify (-10- square root of 125)/5. −10−√1255 - 10 - 125 5. Simplify the numerator.
Surd functions are expressed as a function of square root. The simplified form of the surd expression is 5√5
Simplifying surd functionsSurd functions are expressed as a function of square root.
Given the surd expression
2√125−5√5
Simplify √125
√125 = √25 * 5
√125 = 5√5
Take the difference
2√125−5√5 = 2(5√5) - 5√5
2√125−5√5 = 10√5 - 5√5
2√125−5√5 = 5√5
Hence the simplified form of the surd expression is 5√5
Learn more on surd here: https://brainly.com/question/840021
Related Questions
What are the domain and range of the function represented by the set of ordered pairs? \ (-6,5),(-3,2),(-1,0),(5,-4)\
Answers
Answer:
The domain and the range of the function represented by the set of ordered pairs are {-6, -3, -1, 5} and {5, 2, 0, -4}
Step-by-step explanation:
In any set of ordered pairs,
The domain is the values of x (set of x) ⇒ the first number in each ordered pairThe range is the value of y (set of y) ⇒ the second number in each ordered pairLet us solve the question
∵ The set of ordered pairs is {(-6, 5), (-3, 2), (-1, 0), (5, -4)}
∵ The first number in each ordered pair represents x
∴ x = -6, -3, -1, 5
∵ The set of x is the domain of the function
∴ The domain of the set of ordered pairs = {-6, -3, -1, 5}
∵ The second number in each ordered pair represents y
∴ y = 5, 2, 0, -4
∵ The set of y is the range of the function
∴ The range of the set of ordered pairs = {5, 2, 0, -4}
The domain and the range of the function represented by the set of ordered pairs are {-6, -3, -1, 5} and {5, 2, 0, -4}
Answer:
Domain: {-6,-3,-1,5}
Range: {-4,0,2,5}
Step-by-step explanation:
Find the average (mean) of the following test scores
83,92,47,78,80
A.76
B.70
C.72
D.83
E.68
Answers
Answer:
A
Step-by-step explanation:
Step by step explanation
In Exercises 35 through 42, the slope f'(x) at each point (x, y) on a curve y = f(x) is given along with a particular point (a, b) on the curve. Use this information to find f(x). 35. f'(x) = 4x + 1; (1, 2) 36. f'(x) = 3 – 2x; (0, -1) 37. f'(x) = -x(x + 1); (-1, 5) 38. f'(x) = 3x² + 6x – 2; (0, 6) 2 39. f'(x) = x? + 2; (1, 3) 2 - 1/2 + x; (1, 2) 40. f'(x) = x 41. f'(x) = e-* + x?; (0, 4) 3 42. f'(x) 4; (1, 0) х
Answers
The respective functions f(x) obtained from the given derivatives and points are
35. f(x) = 2x² + x - 1.
36. f(x) = 3x - x² - 1.
37. f(x) = -x²/2 - x³/3 + 9/2.
38. f(x) = x³ + 3x² - 2x + 6.
39. f(x) = (1/4)x⁴ + 2/x + 2x - 19/4.
40. f(x) = 2x⁽¹/²⁾ + (1/2)x² + 1/2.
41. f(x) = -e⁽⁻ˣ⁾ + (1/2)x² + 5.
42. f(x) = 3ln|x| - 4x + 4.
To find the function f(x) based on the given derivative f'(x) and a particular point (a, b), we can integrate f'(x) with respect to x and then use the given point to determine the constant of integration.
Let's go through each exercise:
35. f'(x) = 4x + 1; (1, 2)
Integrating f'(x) gives:
f(x) = 2x² + x + C
Using the given point (1, 2), we can substitute x = 1 and y = 2 into the equation:
2 = 2(1)² + 1 + C
2 = 2 + 1 + C
C = -1
Therefore, f(x) = 2x² + x - 1.
36. f'(x) = 3 - 2x; (0, -1)
Integrating f'(x) gives:
f(x) = 3x - x² + C
Using the given point (0, -1), we can substitute x = 0 and y = -1 into the equation:
-1 = 0 + 0 + C
C = -1
Therefore, f(x) = 3x - x² - 1.
37. f'(x) = -x(x + 1); (-1, 5)
Integrating f'(x) gives:
f(x) = -x²/2 - x³/3 + C
Using the given point (-1, 5), we can substitute x = -1 and y = 5 into the equation:
5 = -(-1)²/2 - (-1)³/3 + C
5 = -1/2 + 1/3 + C
C = 27/6 = 9/2
Therefore, f(x) = -x²/2 - x³/3 + 9/2.
38. f'(x) = 3x² + 6x - 2; (0, 6)
Integrating f'(x) gives:
f(x) = x³ + 3x² - 2x + C
Using the given point (0, 6), we can substitute x = 0 and y = 6 into the equation:
6 = 0 + 0 - 0 + C
C = 6
Therefore, f(x) = x³ + 3x² - 2x + 6.
39. f'(x) = x³ - 2/x² + 2; (1, 3)
Integrating f'(x) gives:
f(x) = (1/4)x⁴ + 2/x + 2x + C
Using the given point (1, 3), we can substitute x = 1 and y = 3 into the equation:
3 = (1/4)(1)⁴ + 2/1 + 2(1) + C
3 = 1/4 + 2 + 2 + C
C = -19/4
Therefore, f(x) = (1/4)x⁴ + 2/x + 2x - 19/4.
40. f'(x) = x⁽⁻¹/²⁾ + x; (1, 2)
Integrating f'(x) gives:
f(x) = 2x⁽¹/²⁾ + (1/2)x² + C
Using the given point (1, 2), we can substitute x = 1 and
y = 2 into the equation:
2 = 2(1)⁽¹/²⁾ + (1/2)(1)² + C
2 = 2 + 1/2 + C
C = 1/2
Therefore, f(x) = 2x⁽¹/²⁾ + (1/2)x² + 1/2.
41. f'(x) = e⁽⁻ˣ⁾ + x; (0, 4)
Integrating f'(x) gives:
f(x) = -e⁽⁻ˣ⁾ + (1/2)x² + C
Using the given point (0, 4), we can substitute x = 0 and y = 4 into the equation:
4 = -e⁽⁻⁰⁾+ (1/2)(0)² + C
4 = -1 + 0 + C
C = 5
Therefore, f(x) = -e⁽⁻ˣ⁾ + (1/2)x² + 5.
42. f'(x) = 3/x - 4; (1, 0)
Integrating f'(x) gives:
f(x) = 3ln|x| - 4x + C
Using the given point (1, 0), we can substitute x = 1 and y = 0 into the equation:
0 = 3ln|1| - 4(1) + C
0 = 0 - 4 + C
C = 4
Therefore, f(x) = 3ln|x| - 4x + 4.
These are the respective functions f(x) obtained from the given derivatives and points.
Learn more about Derivatives here
https://brainly.com/question/29020856
#SPJ4
a linear function has an x-intercept of −8 − 8 and a y-intercept of 4 4 . which of these is an equation of the linear function?
Answers
So, y = (1/2)(x + 8) is the equation of the linear function.
To write the equation of a linear function with a given x-intercept and y-intercept, we can use the point-slope form of a linear equation:
y - y1 = m(x - x1)
In this case, we are given that the x-intercept is (-8, 0) and the y-intercept is (0, 4). We can use the coordinates of the x-intercept as (x1, y1) and the slope of the line as m to write the equation:
y - 0 = m(x - (-8))
y = m(x + 8)
We can then substitute the y-intercept into this equation to find the value of m:
4 = m(0 + 8)
4 = 8m
m = 1/2
Substituting the value of m back into the equation, we get:
y = (1/2)(x + 8)
This is the equation of the linear function.
To learn more about Linear Function,
visit; brainly.com/question/20286983
#SPJ4
y - y1 = m(x - x1)
y - 0 = m(x - (-8))
y = m(x + 8)
We can then substitute the y-intercept into this equation to find the value of m:
4 = m(0 + 8)
4 = 8m
m = 1/2
Substituting the value of m back into the equation, we get:
y = (1/2)(x + 8)
Which statement correctly describes the relationship between the graph of f(x)= x and the graph of g(x) = f (x-10)
The graph of g (x) is the graph of f (x) translated 10 units right.
The graph of g(x) is the graph of f (x) vertically compressed by a factor of 10
The graph of g (x) is the graph of f(x) translated 10 units left
The graph of g (x) is the graph of f (x) vertically stretched by a factor of 10
Answers
Answer:
C The graph of g (x) is the graph of f(x) translated 10 units left
Step-by-step explanation:
9 of 119 of 11 Items
Question
Jillian and Jacob are playing a game where they have to collect blue and yellow tokens. Blue and yellow tokens are worth a different amount of points. Jillian has collected 4 blue tokens and 7 yellow tokens and has 95 points. Jacob has collected 4 blue tokens and 3 yellow tokens and has 75 points. How many points are a blue token and a yellow token worth?
Answers
Using the unitary method, we found that one yellow token is worth 13.57 points and one blue token is worth 8.57 points.
Let's first find the value of one yellow token. We know that Jillian has collected 7 yellow tokens and has a total of 95 points. Therefore, the value of 1 yellow token can be found using the unitary method as follows:
1 yellow token = 95 / 7
1 yellow token = 13.57
Therefore, one yellow token is worth 13.57 points.
Therefore, the value of 4 blue tokens can be found using the unitary method as follows:
4 blue tokens = 75 - (3 x 13.57)
4 blue tokens = 34.29
Now, we know that 4 blue tokens are worth 34.29 points. To find the value of one blue token, we can use the unitary method again as follows:
1 blue token = 34.29 / 4
1 blue token = 8.57
Therefore, one blue token is worth 8.57 points.
To know more about unitary method here
https://brainly.com/question/28276953
#SPJ4
(Chapter 14) If f(x,y) has two local maximal, then f must have a local minimum.TrueFalse
Answers
It is true that the existence of two local maxima does not guarantee the presence of a local minimum. It is possible for a function to have multiple local maxima and no local minimum.
For example, consider the function f(x,y) = x^4 - 4x^2 + y^2. This function has two local maxima at (2,0) and (-2,0), but no local minimum. Therefore, the statement "if f(x,y) has two local maximal, then f must have a local minimum" is false. The presence or absence of local maxima and minima depends on the behavior of the function in the immediate vicinity of a point, and cannot be determined solely based on the number of local maxima. It is possible for a function to have an infinite number of local maxima and minima, or none at all. Therefore, it is important to carefully analyze the behavior of a function in order to determine the presence or absence of local extrema.
Know more about maxima here:
https://brainly.com/question/31387277
#SPJ11
Helppp!!!!!!!!!!!!!!!!!!!!!

Answers
The value of x is equal to 15°
How to determine the value of x?In Mathematics and Geometry, the sum of the exterior angles of both a regular and irregular polygon is always equal to 360 degrees.
Note: The given geometric figure (regular polygon) represents a pentagon and it has 5 sides.
By substituting the given parameters, we have the following:
3x + 4x + 8 + 5x + 5 + 6x - 1 + 5x + 3 = 360°.
3x + 4x + 5x + 6x + 5x + 8 + 5 - 1 + 3 = 360°.
23x + 15 = 360°.
23x = 360 - 15
23x = 345
x = 345/23
x = 15°.
Read more on sum of interior angles here: brainly.com/question/13293407
#SPJ1
what is 3/16 x 6 in simplest form as fraction
how do u solve dis
Answers
Answer:
9/8
Step-by-step explanation:
3/16 x 6
= 3/16 x 6/1
= 18/16
= 9/8
I am very confused about this but only need the answer.
Please Help


Answers
Answer:
C
Step-by-step explanation:
The radius of circle 2 is bigger than circle one, so the diameter will be bigger too.
The circumference of the circle 1 is less than the circumference of the circle 2.
What is circumference?Circumference is "a distance around the circle".
According to the question,
The area of the circle 1 is 6π and the area of the circle 2 is 7π.
Area of the circle = π.r²
Radius of the circle 1 is less than the radius of the circle 2 this implies diameter of the circle 2 is greater than diameter of the circle 1.
Hence, the circumference of the circle 1 is less than the circumference of the circle 2.
Learn more about circumference here
https://brainly.com/question/15446091
#SPJ2
3. When x = 6, which number is closest to the value of y on the line of best fit in the graph below?
09
01
07
10
0987
65
432
2
1
➤X
0 1 2 3 4 5 6 7 8 9 10
Answers
Answer:
9
Step-by-step explanation:
PLS HELP AND EXPLAINNN
Find the area of a circle with a radius of 9
i know the formula but im doing something wrong i need help
Answers
Answer:
A≈254 cm^2
Step-by-step explanation:
The area of a circle is given by formula: π r^2
π has a constant value of 3.14 And the radius of the circle is 9 c m
the area= π r^2 = 3.14 x (9)^2 cm^2
= 3.14 × ( 81 )
= 254.34 c m^2
≈ 254 c m^2
use the binomial theorem to find the binomial expansion of the given expression. (2x-3y)^5.
show work
Answers
Answer:
(a + b)^n = C(n, 0)a^n b^0 + C(n, 1)a^(n-1) b^1 + C(n, 2)a^(n-2) b^2 + ... + C(n, n-1)a^1 b^(n-1) + C(n, n)a^0 b^n
The binomial expansion of (2x - 3y)^5 is:
32x^5 - 240x^4y + 720x^3y^2 - 1080x^2y^3 + 810xy^4 - 243y^5
The binomial expansion of the given expression is 32x⁵+240x⁴y+720x³y²+1080x²y³+810xy⁴+243y⁵.
The given expression is (2x-3y)⁵.
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial.
(2x)⁵+⁵c₁(2x)⁴(3y)¹+⁵C₂(2x)³(3y)²+⁵C₃(2x)²(3y)³+⁵C₄(2x)(3y)⁴+⁵C₅(3y)⁵
= 32x⁵+5(16x⁴)(3y)+10.(8x³)(9y²)+10(4x²)(27y³)+5(2x)(81y⁴)+243y⁵
= 32x⁵+240x⁴y+720x³y²+1080x²y³+810xy⁴+243y⁵
Therefore, the binomial expansion of the given expression is 32x⁵+240x⁴y+720x³y²+1080x²y³+810xy⁴+243y⁵.
To learn more about the binomial expansion visit:
https://brainly.com/question/31363254.
#SPJ2
Shondra was unsure about what career to go into. Her high school counselor suggested a personal assessment to point out Shondra’s interests. The assessment revealed that Shondra is very passionate about justice and making sure that people stay safe and treat each other fairly. Shondra also enjoys physical fitness and can handle risky high-pressure situations well.
Shondra would be well suited for which career cluster. Select three options.
Answers
Answer:
lawer, Police officer criminal justice
Solve the equation for the indicated variable.
1/R = 1/R1+1/R2 ; for R2
R2 = ?
Answers
The solution for R2 is:
R2 = (R1*R)/(R1+R)
We can begin by multiplying both sides of the equation by the product of R2 and R1 to eliminate the denominators:
1/R = 1/R1 + 1/R2
Multiplying both sides by R1*R2:
R1R2(1/R) = R1R2(1/R1) + R1R2(1/R2)
Simplifying:
R2 = (R1*R)/((R1+R))
Therefore, the solution for R2 is:
R2 = (R1*R)/(R1+R)
Learn more about equation here:
https://brainly.com/question/29657983
#SPJ11
House Loan
Cost: $450,000
Length of Loan: 30 Years
Simple Interest Rate: 6.00%
Yearly Taxes: $2,000
Yearly Insurance: $1,500
What are your Monthly Payments with taxes & insurance:
Answers
Step-by-step explanation:
Your monthly payments with taxes and insurance included would be $2,903.71. This is calculated by taking the loan amount of $450,000 and multiplying it by the simple interest rate of 6.00%. The result is $27,000, which is then divided by the length of the loan, 30 years. This gives you
the principal and interest portion of your monthly payment, which is $2,033.33. To that, you add your yearly taxes of $2,000 and insurance of $1,500, divided by 12 months, to get an additional $416.67 and $125, respectively. Adding these two numbers together gives you your total monthly payment of $2,903.71.
A builder wants to build a sump to store water in an apartment. The volume of the
rectangular sump will be modelled by V(x) = x3 + x2 - 4x - 4.
He planned in such a way that its length and breadth are (x + 1) and (x - 2) respectively.
How much he has to dig?
(a) (x + 1]
(b) (x - 2)
(c) (x-3)
(d) (x + 2)
(ii) If x = 4 meter, what is the storage capacity (in litres) of this sump?
(iii) A ladder is kept a point halfway from the base as shown in the figure. It just touches
the top of the sump. Find the length of the ladder, assuming x-42 (correct to 1 dp)
Answers
Answer:
1) b, 2) d, 3) dStep-by-step explanation:
The volume is the product of three dimensions
V = lwhGiven:
w = x + 1, l = x + 2 and V(x) = x³ + x² - 4x - 4
1) Let's find the height:
x³ + x² - 4x - 4 =x²(x + 1) - 4(x + 1) = (x² -4)(x + 1) = (x + 2)(x - 2)(x + 1)We got h = x - 22) x = 4 m
Volume is:
V = 4³ + 4² - 4*4 - 4 = 60 m³3) x = 4 m
Dimensions are:
w = x + 1 = 5 m, l = x + 2 = 6 m, h = x - 2 = 2 mFull surface area is:
2(lw + lh + wh) =2(5*6 + 6*2 + 5*2) = 104 m²Solve for b
a) 2b x 3 = 6 c) 6 + 7b = 41
b) 32 - 3b = 2 d) 100/ 5b = 2
Answers
a) The solution for b in the equation 2b × 3 = 6 is b = 1.
b) The solution for b in the equation 32 - 3b = 2 is b = 10.
c) The solution for b in the equation 6 + 7b = 41 is b = 5.
d) The solution for b in the equation 100/5b = 2 is b = 10.
a) To solve for b in the equation 2b × 3 = 6, we can start by dividing both sides of the equation by 2 to isolate b.
2b × 3 = 6
(2b × 3) / 2 = 6 / 2
3b = 3
b = 3/3
b = 1
Therefore, the solution for b in the equation 2b × 3 = 6 is b = 1.
c) To solve for b in the equation 6 + 7b = 41, we can start by subtracting 6 from both sides of the equation to isolate the term with b.
6 + 7b - 6 = 41 - 6
7b = 35
b = 35/7
b = 5
Therefore, the solution for b in the equation 6 + 7b = 41 is b = 5.
b) To solve for b in the equation 32 - 3b = 2, we can start by subtracting 32 from both sides of the equation to isolate the term with b.
32 - 3b - 32 = 2 - 32
-3b = -30
b = (-30)/(-3)
b = 10
Therefore, the solution for b in the equation 32 - 3b = 2 is b = 10.
d) To solve for b in the equation 100/5b = 2, we can start by multiplying both sides of the equation by 5b to isolate the variable.
(100/5b) × 5b = 2 × 5b
100 = 10b
b = 100/10
b = 10.
Therefore, the solution for b in the equation 100/5b = 2 is b = 10.
In summary, the solutions for b in the given equations are:
a) b = 1
c) b = 5
b) b = 10
d) b = 10
For similar question on equation.
https://brainly.com/question/30451972
#SPJ8
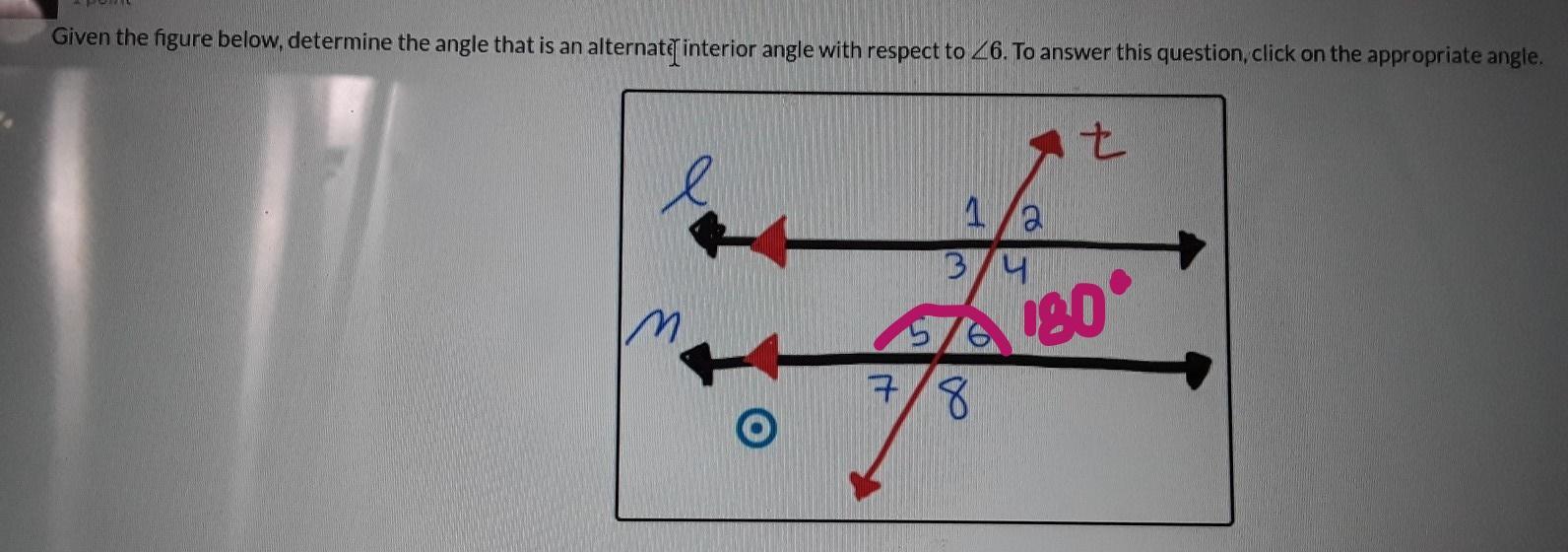
Given the figure below, determine the angle that is an alternate interior angle with respect to. 1. To answer this question, click on the appropriate angle.

Answers
In this case, the alternate interior angles are for example angles 6 and 3 because they are on the inner side of each of the lines (m and l) but on opposite sides of the transversal (t).
m∠6 = m∠3
or
m∠4 = m∠5
If each dimension of the cylinder is doubled, how many
times larger will the volume of the cylinder be?
Answers
An animal rescue group recorded the number of adoptions that occurred each week for three weeks:
. There were x adoptions during the first week.
• There were 10 more adoptions during the second week than during the first week.
There were twice as many adoptions during the third week as during the first week.
There were a total of at least 50 adoptions from the animal rescue group during the three weeks.
Write an inequality that represents all possible values of x, the number of adoptions from the animal rescue group during the first week.
Answers
An inequality that represents all possible values of x is; x ≤ 10
How to solve Inequality word problems?We are given that there were x number of adoptions during the first week.
We are told that there were 10 more adoptions during the second week than during the first week. Thus;
number of adoptions in second week = 10 + x adoptions
There were twice as many adoptions during the third week as during the first week. Thus;
Number of adoptions in third week = 2x adoptions
There were a total of 50 adoptions from the animal rescue group during the three weeks. Thus, we can say that;
x + 10 + x + 2x ≤ 50
4x ≤ 50 - 10
4x ≤ 40
x ≤ 10
Read more about Inequality Word Problems at; https://brainly.com/question/25275758
#SPJ1
I WILL GIVE YOU BRAINLY PLSS
There are 256 vehicles in a car dealership’s lot. At least 113 of them are hybrid
vehicles. Which inequality describes how many vehicles, at most, are not hybrid?
A. ≤ 143
B. 143
D. ≥ 143
PLSS SHOW YOUR WORK PLS
Answers
Answer:
B. 143
Step-by-step explanation:
Subtract 113 from 256 and you get 143. 143 is not less than or greater than 143 so it is equal.
rea and Bryan are auditioning for a part in the school play. There are 15 people auditioning, and the order of their auditions are chosen at random. Find the probability that Drea auditions last and Bryan auditions second to last.]
Answers
Explanation:
The positions of Drea and Bryan are locked in as last, and 2nd to last respectively. This means the 15 slots drops to 15-2 = 13 slots.
There are 13 other people and 13 slots to fill.
That gives 13*12*11*10*9*8*7*6*5*4*3*2*1 = 6,227,020,800 different permutations where Drea is last and Bryan is 2nd to last. Order matters in a permutation.
This is out of 15*14*13*12*11*10*9*8*7*6*5*4*3*2*1 = 1,307,674,368,000 different ways to arrange the 15 people. This larger count will have Drea and Bryan move to other slots.
If you divide the smaller number over the larger, then the block "13*12*11*10*9*8*7*6*5*4*3*2*1" cancels out.
We'll be left with 1/(15*14) = 1/210 as the final answer
Please help mee!!! Will give brainliest!

Answers
Answer:
B.11+7=18
Step-by-step explanation:
its B because since its 7 days AFTER it means your going to have to add the 11 days plus this 7 days. Which would give you 18 days left till Susie's concert.
A single number that estimates the value of an unknown parameter is called a _______ estimate.
Answers
Answer:
A single number that estimates the value of an unknown parameter is called a point estimate.
Step-by-step explanation:
Don't see the point (haha) of elaborating
Lee's paper clip is 32 feet long. He is going to add paper clips continually for the next eight hours. At the end of eight hours, the chain is 80 feet long. Find the unite rate of growth in feet per hour. Be sure to show your work and label your answer!
PLEASE HELP ME !
Answers
Answer:
6ft/hour
Step-by-step explanation:
Answer:
6 feet/hour
Step-by-step explanation:
I first found out exactly the amount of feet that was added. \(80-32=48\)
Then I divided that by the amount of hours. 48 ÷ 8 = 6
Jayden had pizza delivered. Jayden tips $5 for deliveries or 10% of the purchase, whichever is higher. The pizza delivered cost $29.50.
How much will Jayden tip?
Answers
Answer:
Five dollars?
Step-by-step explanation:
I don’t fully understand the question, so apologies if I am incorrect!
Choose all the numbers that are common multiples of 8 and 3.
3
12
24
38
48
72
Answers
Answer:
24, 48, and 72 are all multiples of 8
3, 12, and 24 are multiples of 3
Step-by-step explanation:
(Find the mean from the group of numbers) Help me please and thank you!

Answers
Answer:
mean = 3
Step-by-step explanation:
The mean of a data set is the average of all the elements in the set. This can be calculated using the formula:
\(\text{mean} = \dfrac{\text{sum of elements}}{\text{number of elements}}\)
From the bar graph, we can determine the total number of elements in the data set by counting the number of Xs.
We can see that there are 11 elements in the data set.
We can also determine the number of Xs for each number of times that a person played mini-golf last summer:
0, 1, 2, (5 × 3), 4, 5, 6
Now, we can plug these values into the above formula to calculate the mean.
\(\text{mean} = \dfrac{0+1+2+5(3) + 4 + 5 + 6}{11}\)
\(\text{mean} = \dfrac{33}{11}\)
\(\boxed{\text{mean} = 3}\)
the bob of a pendulum 0.4m long is 4cm higher at the top of its swing than its bottom. Find the angle of swing on each side of the vertical
Answers
Answer:
\(\theta=25.84^\circ\)
Step-by-step explanation:
Pendulum
The length of the pendulum is 0.4 m or 40 cm. When swinging, it reaches the top height of 4 cm from the bottom. The geometric construction of this situation is shown in the image below.
The right triangle is formed by the length of the pendulum (40 cm), its horizontal displacement, and the vertical height projected by the pendulum.
This last distance is calculated subtracting the total length of the pendulum and the vertical displacement reached in its higher position.
We need to calculate the angle θ, for which we'll use the cosine since we know the adjacent leg and the hypotenuse:
\(\displaystyle \cos\theta=\frac{36}{40}=0.9\)
The angle is
\(\theta=\cos^{-1}(0.9)=25.84^\circ\)
\(\boxed{\theta=25.84^\circ}\)
