si un angulo mide t6 cual es su medida en grados
Answers
Step-by-step explanation:
No sé la respuesta exactamente, pero cuando la traduje decía T6, ¿qué es eso?
Related Questions
One runner had a personal best time, and the other runner neither trained nor had a personal best time
Answers
While one runner demonstrated dedication and improvement through a personal best time, the other runner's lack of training and absence of a personal best time suggest a more casual or unprepared approach to the race.
In a race between two runners, one of them had a personal best time, while the other runner neither trained nor had a personal best time.
The runner who had a personal best time implies that they had trained and put in effort to improve their performance. A personal best time suggests that they have achieved their highest level of performance in a race. This indicates that the runner has dedicated time and effort to their training regimen, focusing on improving their speed and endurance.
On the other hand, the runner who neither trained nor had a personal best time implies that they did not invest effort in training or actively seek to improve their performance. They may have participated in the race casually or without specific training goals in mind. As a result, they did not achieve a personal best time, indicating that they did not put in the necessary effort to reach their full potential.
In summary, while one runner demonstrated dedication and improvement through a personal best time, the other runner's lack of training and absence of a personal best time suggest a more casual or unprepared approach to the race.
For more such questions on dedication, click on:
https://brainly.com/question/30160240
#SPJ8
Angle TLN equals (3X -18)°, angle MZQ equals (5X +14)° and

Answers
For the given figure, x = 23° and y = 129°
Parallel lines:
Parallel lines are lines that always stay the same distance apart and never meet.
Transversal line :
A transversal is a line that crosses two or more other lines.
given,
∠TLN = (3x - 18)°
∠MZQ = (5x + 14)°
∠NLM = y°
Now,
∠MZP + ∠MZQ = 180° (Linear Pair)
∠MZP = 180° - ∠MZQ ...........(I)
again,
∠NLM + ∠TLN =180° ...........(II) (Linear Pair)
As, ∠TLN = ∠MZP (Corresponding Angle)
(3x - 18)° = 180° - ∠MZQ
(3x - 18)° = 180° - (5x + 14)°
3x + 5x = 180° - 14° + 18°
8x = 184°
x = 184 / 8
x = 23°
From (II),
∠NLM + ∠TLN =180°
y° + 3x - 18° = 180°
y = 180 - 3x + 18
= 180 - 3* 23 + 18
= 180 - 69 +18
y = 129°
For the given figure,
x = 23° and y = 129°
To learn more about Parallel line visit:
https://brainly.com/question/17432060
#SPJ9
The area model shows 2 1 4
What is 2 x 2 1/4?
2 1/2
2 3/4
4 1/4
4 1/2
Answers
Answer:
4 1/2
Step-by-step explanation:Because 2x2 =4 and 2x1/4 = 1/2 so it is 4 1/2
Two glasses of milk and three snack bars have a total of 72 carbs. and 4 glasses of milk and 2 snack bars have a total of 88 carbs. Determine how many carbs are one glass of mild and one snack bar.
Answers
Answer:
one glass of milk = 15 carbs
one bar = 14 carbs
Step-by-step explanation:
let 'm' = one glass of milk
let 'b' = one snack bar
system of equations:
2m + 3b = 72
4m + 2b = 88
I used the elimination method and multiplied the 1st equation by -2
-4m - 6b = -144
+ 4m + 2b = 88
-4b = -56
b = 14
now solve for 'm'
2m + 3(14) = 72
2m + 42 = 72
2m = 30
m = 15
If diameter EF bisects BC, what is the angle of intersection?

Answers
Answer:
The angle of the intersection is 90 degrees
Step-by-step explanation:
How I know this is because EF is the diameter, which means that arc EF is equal to 180 degrees. Because we know this that means when it is spilt into two parts, the arc and angle measure has to be 90 degrees.
Another way to do this is to remember that a circle is 360 degrees and the circle is split into 4 parts. So all you have to do is divide 360/4 to get 90. Your answer.
Write an equation of the line satisfying the given conditions. Write the answer in slope-intercept form or standard form. Express numbers as integers or
simplified fractions.
The line contains the point (-3, 6) and is parallel to 3x+3y=2.
The equation of the line is
Answers
The equation of the line is : y = -1x + 3
What is Equation of line?
A straight line's general equation is y = mx + c, where m denotes the gradient and y = c denotes the point at which the line crosses the y-axis. On the y-axis, this value c is referred to as the intercept. Y = mx + c represents the equation of a straight line with gradient m and intercept c on the y-axis.
Given,
3x + 3y = 2
3y = -3x + 2
y = -x + 2/3
Comparing it with
y = mx + c
we get,
m = -1
Now, let the equation of line be
y = mx + c
where, m = -1
Now we have to check for point (0,0) that it satisfies
0 = -1(0) + c
c = 0
So, the equation of line will be y = -1x
Now, let y = mx + c be the equation of line of point (-3, 6) should satisfy]
6 = -1(-3) + c
6 = 3 + c
c = 6 - 3
c = 3
So the equation of line is y = -1x + 3
Hence, The equation of the line is y = -1x + 3
To learn more about Equation of line click on the link
https://brainly.com/question/18831322
#SPJ1
I need help bad! Will give 5 stars asap i need help

Answers
Answer:
5 or 6 I hope i helped YOU!!!!!
Step-by-step explanation:
Helpppppp once again plssss?! Thank you

Answers

Heeeelp please, Can be zero or not?
with all steps and explanay.

Answers
The value of integral is 3.
Let's evaluate the integral over the positive half of the interval:
∫[0 to π] (cos(x) / √(4 + 3sin(x))) dx
Let u = 4 + 3sin(x), then du = 3cos(x) dx.
Substituting these expressions into the integral, we have:
∫[0 to π] (cos(x) / sqrt(4 + 3sin(x))) dx = ∫[0 to π] (1 / (3√u)) du
Using the power rule of integration, the integral becomes:
∫[0 to π] (1 / (3√u)) du = (2/3) . 2√u ∣[0 to π]
Evaluating the definite integral at the limits of integration:
(2/3)2√u ∣[0 to π] = (2/3) 2(√(4 + 3sin(π)) - √(4 + 3sin(0)))
(2/3) x 2(√(4) - √(4)) = (2/3) x 2(2 - 2) = (2/3) x 2(0) = 0
So, the value of integral is
= 3-0
= 3
Learn more about Definite integral here:
https://brainly.com/question/30760284
#SPJ1
Answer:
\(3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x\approx 0.806\; \sf (3\;d.p.)\)
Step-by-step explanation:
First, compute the indefinite integral:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x\)
To evaluate the indefinite integral, use the method of substitution.
\(\textsf{Let} \;\;u = 4 + 3 \sin x\)
Find du/dx and rewrite it so that dx is on its own:
\(\dfrac{\text{d}u}{\text{d}x}=3 \cos x \implies \text{d}x=\dfrac{1}{3 \cos x}\; \text{d}u\)
Rewrite the original integral in terms of u and du, and evaluate:
\(\begin{aligned}\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\int \dfrac{\cos x}{\sqrt{u}}\cdot \dfrac{1}{3 \cos x}\; \text{d}u\\\\&=\int \dfrac{1}{3\sqrt{u}}\; \text{d}u\\\\&=\int\dfrac{1}{3}u^{-\frac{1}{2}}\; \text{d}u\\\\&=\dfrac{1}{-\frac{1}{2}+1} \cdot \dfrac{1}{3}u^{-\frac{1}{2}+1}+C\\\\&=\dfrac{2}{3}\sqrt{u}+C\end{aligned}\)
Substitute back u = 4 + 3 sin x:
\(= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
Therefore:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
To evaluate the definite integral, we must first determine any intervals within the given interval -π ≤ x ≤ π where the curve lies below the x-axis. This is because when we integrate a function that lies below the x-axis, it will give a negative area value.
Find the x-intercepts by setting the function to zero and solving for x in the given interval -π ≤ x ≤ π.
\(\begin{aligned}\dfrac{\cos x}{\sqrt{4+3\sin x}}&=0\\\\\cos x&=0\\\\x&=\arccos0\\\\\implies x&=-\dfrac{\pi }{2}, \dfrac{\pi }{2}\end{aligned}\)
Therefore, the curve of the function is:
Below the x-axis between -π and -π/2.Above the x-axis between -π/2 and π/2.Below the x-axis between π/2 and π.So to calculate the total area, we need to calculate the positive and negative areas separately and then add them together, remembering that if you integrate a function to find an area that lies below the x-axis, it will give a negative value.
Integrate the function between -π and -π/2.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_1=-\displaystyle \int^{-\frac{\pi}{2}}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=- \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{-\frac{\pi}{2}}_{-\pi}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(-\pi\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (-1)}+\dfrac{2}{3}\sqrt{4+3 (0)}\\\\&=-\dfrac{2}{3}+\dfrac{4}{3}\\\\&=\dfrac{2}{3}\end{aligned}\)
Integrate the function between -π/2 and π/2:
\(\begin{aligned}A_2=\displaystyle \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\\\\&=\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}\\\\&=\dfrac{2}{3}\sqrt{4+3 (1)}-\dfrac{2}{3}\sqrt{4+3 (-1)}\\\\&=\dfrac{2\sqrt{7}}{3}-\dfrac{2}{3}\\\\&=\dfrac{2\sqrt{7}-2}{3}\end{aligned}\)
Integrate the function between π/2 and π.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_3=-\displaystyle \int^{\pi}_{\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= -\left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\pi}_{\frac{\pi}{2}}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(\pi\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (0)}+\dfrac{2}{3}\sqrt{4+3 (1)}\\\\&=-\dfrac{4}{3}+\dfrac{2\sqrt{7}}{3}\\\\&=\dfrac{2\sqrt{7}-4}{3}\end{aligned}\)
To evaluate the definite integral, sum A₁, A₂ and A₃:
\(\begin{aligned}\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\dfrac{2}{3}+\dfrac{2\sqrt{7}-2}{3}+\dfrac{2\sqrt{7}-4}{3}\\\\&=\dfrac{2+2\sqrt{7}-2+2\sqrt{7}-4}{3}\\\\&=\dfrac{4\sqrt{7}-4}{3}\\\\ &\approx2.194\; \sf (3\;d.p.)\end{aligned}\)
Now we have evaluated the definite integral, we can subtract it from 3 to evaluate the given expression:
\(\begin{aligned}3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x&=3-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9}{3}-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9-(4\sqrt{7}-4)}{3}\\\\&=\dfrac{13-4\sqrt{7}}{3}\\\\&\approx 0.806\; \sf (3\;d.p.)\end{aligned}\)
Therefore, the given expression cannot be zero.

If the circumference of a circle is known, how can the radius be found?

Answers
Answer:
the equation to find radius from circumference is r = C2pi
B
Step-by-step explanation:
i need help. this is algebra 2 and im currently going “bootcamp for it*

Answers
Answers:
8
6
1
3
Reason:
Add 5 to each value in the f(x) column.
Example: 3+5 = 8 for the first row.
This will shift each point 5 units up. This is because we're moving 5 units up the y axis.
Harshini rode her bicycle 13.76 kilometers on Monday, 9.8 kilometers on Wednesday, and 16.415 kilometers on Friday. She used the addition below to determine the total distance she rode over the three days. 13.76 + 9.8 + 16.415 = 39.975. All decimal points are aligned. Which method determines whether her answer is reasonable?
A.) Remove the decimal points and add 137 + 98 + 16415 = 17,889; since 17,889 is not close to 39.975, her answer is not reasonable.
B.) Round all the numbers to 20; since 20 + 20 + 20 = 60 and 60 is not close to 39.975, her answer is not reasonable.
C.) Round all the numbers to 10; since 10 + 10 + 10 = 30 and 30 is close to 39.975, her answer is reasonable.
D.) Round 13.76 to 14, round 9.8 to 10, and round 16.415 to 16; since 14 + 10 + 16 = 40 and 40 is close to 39.975, her answer is reasonable.
Answers
Answer: AKA B
Step-by-step explanation:
Answer:
B
Step-by-step explanation:
Find the value of f(3) for the function. f(3)=-5(x+5)
Answers
Answer:
Step-by-step explanation:
f(3)=-5(x+5)
=5(3) +5
=15+5
f(3) =20
A bag contains n counters.
One counter is blue and the rest are red.
Two counters are taken at random from the bag.
a) Express, in terms of n, the probability that a counter of each colour is taken.
Give your answer as a fraction in its simplest form.
b) The probability that a counter of each colour is taken is 0.125
How many red counters are in the bag?
Answers
Answer:
Step-by-step explanation:
a) If we denote the number of red counters as R and the number of blue counters as B, then the probability of selecting one counter of each color is:
P(one red and one blue) = (R/(R+B)) * (B/(R+B-1)) = R * B / (R+B)(R+B-1)
We can simplify this expression by canceling the common factors of R and B:
P(one red and one blue) = (R * B) / (R+B)(R+B-1) = (R * B) / (R^2 + 2RB + B^2 - R - B)
Simplifying further, we get:
P(one red and one blue) = (R * B) / (R^2 - R + B^2 - B)
Since we want to express this probability in terms of n, we can substitute R + B = n to get:
P(one red and one blue) = (R * (n-R)) / (R^2 - R + (n-R)^2 - (n-R))
Simplifying again, we get:
P(one red and one blue) = (R * (n-R)) / (R^2 - 2Rn + n^2 + R)
Finally, we can simplify this expression to get:
P(one red and one blue) = (R * (n-R)) / (n(n-1))
This is the probability of selecting one red and one blue counter.
b) If the probability of selecting one red and one blue counter is 0.125, then we can substitute this value into the expression we derived above to solve for the number of red counters:
0.125 = (R * (n-R)) / (n(n-1))
Multiplying both sides by n(n-1) gives:
(0.125) * (n(n-1)) = R * (n-R)
Expanding the right side gives:
(0.125) * (n(n-1)) = R * n - R^2
Rearranging the terms gives:
R^2 - R*n + (0.125) * (n(n-1)) = 0
This is a quadratic equation in R, which we can solve using the quadratic formula:
R = (n +/- sqrt(n^2 - 4*(0.125)*(n(n-1)))) / 2
Substituting the value of (0.125) into the equation gives:
R = (n +/- sqrt(n^2 - 0.5n(n-1))) / 2
We want the positive solution for R, since R must be a positive integer. Therefore, the number of red counters is:
R = (n + sqrt(n^2 - 0.5n(n-1))) / 2
To find the integer value of R, we can round this expression to the nearest integer. For example, if n = 8, then the number of red counters is:
R = (8 + sqrt(8^2 - 0.587)) / 2 = 4.29... ~ 4
If we substitute this value of R back into the equation for the probability of selecting one red and one blue counter, we get:
P(one red and one blue) = (4 * (8-4)) / (8(8-1)) = 0.125
We can check that this value is indeed equal to the given probability of 0.125, so our solution is correct.
Note that we could also have solved for R by substituting the given probability of 0.125 directly into the equation for the probability of selecting one red and one blue counter and solving for R. This would give us the same result.
Find the value of x for the following

Answers
Answer:
x = -2
Step-by-step explanation:
Given angles are,
→ 9x + 96°
→ 7x + 92°
Now we have to,
→ Find the required value of x.
We know that,
→ Vertically opposite angles are equal.
Forming the equation,
→ 9x + 96° = 7x + 92°
Then the value of x will be,
→ 9x + 96° = 7x + 92°
→ 9x - 7x = 92° - 96°
→ 2x = -4
→ x = -4/2
→ [ x = -2 ]
Hence, the value of x is -2.
PLEASE ANWSER QUICK
What is the approximate distance between the points (9,2) and (4,8)?
Answers
Answer:
(5,6)
Step-by-step explanation:
Answer with step-by-step explanation:
(9,2) - (4,8) = (5,-6)
Hope this was helpful! (brainliest please)
Melissa's flower shop got a shipment of 158 roses. She wants to make bouquets of 6 roses each. How many bouquets can Melissa make?
bouquets
How many roses will she have left over?
Answers
A company surveyed 2400 men where 1248 of the men identified themselves as the primary grocery shopper in their household. a) Estimate the percentage of all males who identify themselves as the primary grocery shopper. Use a 98% confidence interval. Check the conditions first. b) A grocery store owner believed that only 43% of men are the primary grocery shopper for their family, and targets his advertising accordingly. He wishes to conduct a hypothesis test to see if the fraction is in fact higher than 43%. What does your confidence interval indicate? Explain. c) What is the level of significance of this test? Explain.
Answers
Answer:
a) With a confidence level of 98%, the percentage of all males who identify themselves as the primary grocery shopper are between 0.4962 and 0.5438.
b) The lower limit of the confidence interval is higher that 0.43, so if he conduct a hypothesis test, he will find that the data shows evidence to said that the fraction is higher than 43%.
c) \(\alpha =1-0.98=0.02\)
Step-by-step explanation:
If np' and n(1-p') are higher than 5, a confidence interval for the proportion is calculated as:
\(p'-z_{\alpha/2}\sqrt{\frac{p'(1-p')}{n} }\leq p\leq p'+z_{\alpha/2}\sqrt{\frac{p'(1-p')}{n} }\)
Where p' is the proportion of the sample, n is the size of the sample, p is the proportion of the population and \(z_{\alpha/2}\) is the z-value that let a probability of \(\alpha/2\) on the right tail.
Then, a 98% confidence interval for the percentage of all males who identify themselves as the primary grocery shopper can be calculated replacing p' by 0.52, n by 2400, \(\alpha\) by 0.02 and \(z_{\alpha/2}\) by 2.33
Where p' and \(\alpha\) are calculated as:
\(p' = \frac{1248}{2400}=0.52\\\alpha =1-0.98=0.02\)
So, replacing the values we get:
\(0.52-2.33\sqrt{\frac{0.52(1-0.52)}{2400} }\leq p\leq 0.52+2.33\sqrt{\frac{0.52(1-0.52)}{2400} }\\0.52-0.0238\leq p\leq 0.52+0.0238\\0.4962\leq p\leq 0.5438\)
With a confidence level of 98%, the percentage of all males who identify themselves as the primary grocery shopper are between 0.4962 and 0.5438.
The lower limit of the confidence interval is higher that 0.43, so if he conduct a hypothesis test, he will find that the data shows evidence to said that the fraction is higher than 43%.
Finally, the level of significance is the probability to reject the null hypothesis given that the null hypothesis is true. It is also the complement of the level of confidence. So, if we create a 98% confidence interval, the level of confidence \(1-\alpha\) is equal to 98%
It means the the level of significance \(\alpha\) is:
\(\alpha =1-0.98=0.02\)
Write and algebraic expression for 10 less than the product of seven and F
Answers
Answer:
f(x) = 7x-10
Step-by-step explanation:
Complete question;
Write and algebraic expression for 10 less than the product of seven and a number.
Let the number be x;
The product of seven and the number is expressed as;
= 7 * x
= 7x
If 10 is less than the product of seven and a number then the expression becomes
7x - 10
The required algebraic expression is f(x) = 7x-10
Use the information given below to find tan(a + B)
cos a = 3/5, with a in quadrant IV
tan B = 4/3, with B in quadrant I I I
Give the exact answer, not a decimal approximation.
tan(a + B) = ?
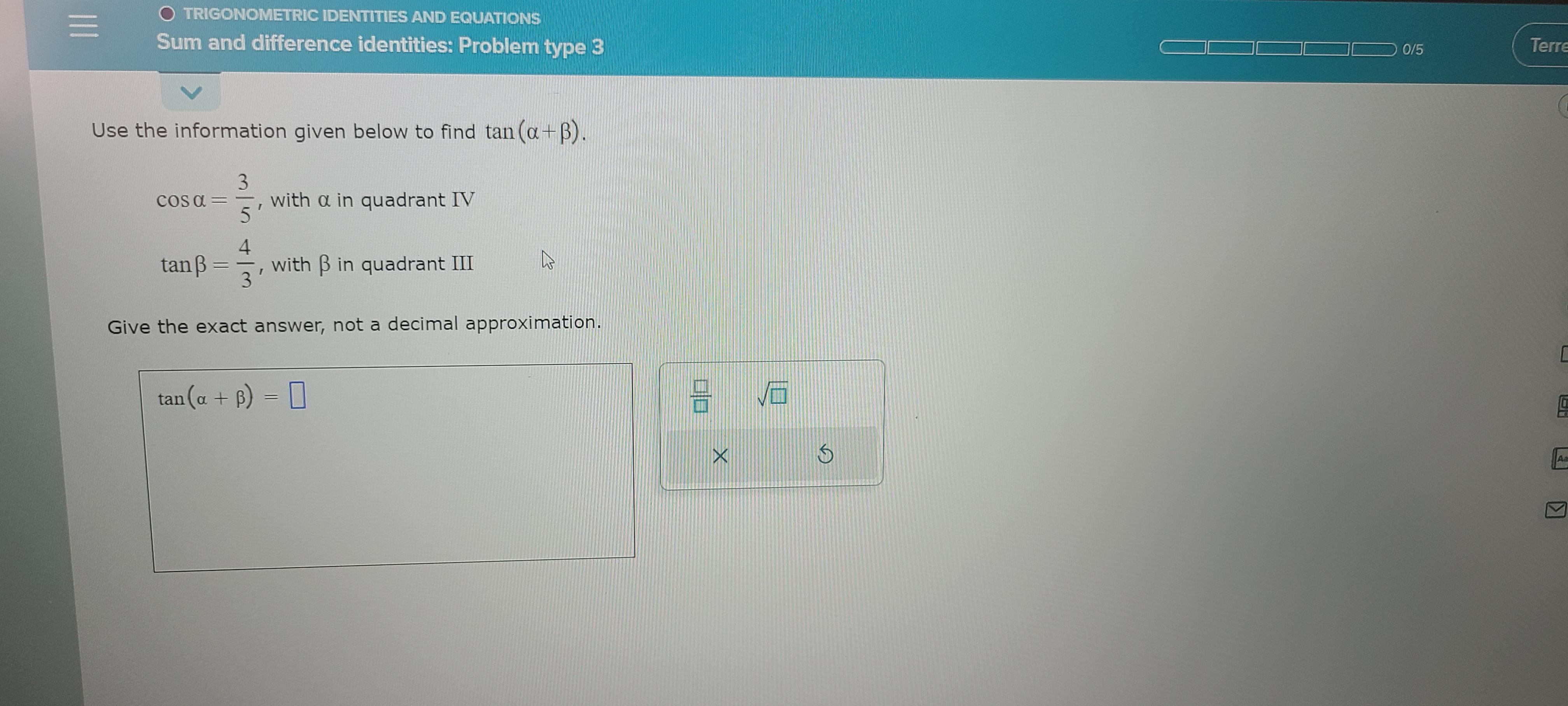
Answers
let's bear in mind that on the III Quadrant, sine and cosine are both negative, whilst on the IV Quadrant, sine is negative and cosine is positive, that said
\(\cos(\alpha )=\cfrac{\stackrel{adjacent}{3}}{\underset{hypotenuse}{5}}\hspace{5em}\textit{let's find the \underline{opposite side}} \\\\\\ \begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies o=\sqrt{c^2 - a^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{5}\\ a=\stackrel{adjacent}{3}\\ o=opposite \end{cases} \\\\\\ o=\pm \sqrt{ 5^2 - 3^2} \implies o=\pm \sqrt{ 16 }\implies o=\pm 4\implies \stackrel{IV~Quadrant }{o=-4} \\\\[-0.35em] ~\dotfill\)
\(\tan(\beta )=\cfrac{\stackrel{opposite}{4}}{\underset{adjacent}{3}}\implies \tan(\beta )=\cfrac{\stackrel{opposite}{-4}}{\underset{adjacent}{-3}} \\\\[-0.35em] ~\dotfill\\\\ \tan(\alpha + \beta) = \cfrac{\tan(\alpha)+ \tan(\beta)}{1- \tan(\alpha)\tan(\beta)} \\\\\\ \tan(\alpha + \beta)\implies \cfrac{ ~~\frac{-4}{3}~~ + ~~\frac{-4}{-3} ~~ }{1-\left( \frac{-4}{3} \right)\left( \frac{-4}{-3} \right)}\implies \cfrac{0}{1-\left( \frac{-4}{3} \right)\left( \frac{-4}{-3} \right)}\implies \text{\LARGE 0}\)
Sammy wants to buy a new stereo priced at $413. He enters into an
agreement to pay $20 a month for 24 months. How much will the finance
charge be for this purchase?
Answers
Answer:
$840
Step-by-step explanation:
20×24=840 so you divide $20 and 24 months and get 840
Suppose that $1000 is deposited into an account where the interest is compounded annually. This situation can be modeled by the function, f(t) = 1000(1.06), where f(t) represents the value (in dollars) of the account at t years after depositing the $1000. 1. In how many years will the money in the account double? 2. According to this model, how much money will the account have in 10 years? 3. According to this model, what is interest rate being earned per year.

Answers
As the initial deposited is $1000
1. In how many years will the money in the acount be 2000
\(\begin{gathered} f(t)=2000 \\ \\ 2000=1000(1.06)^t \end{gathered}\)To solve for t:
-Divide both sides of the equation into 1000
\(\begin{gathered} \frac{2000}{1000}=\frac{1000(1.06)^t}{1000} \\ \\ 2=(1.06)^t \end{gathered}\)- As:
\(\begin{gathered} a^b=c \\ \text{Log}_ac=b \end{gathered}\)\(\begin{gathered} (1.06)^t=2 \\ \log _{1.06}2=t \end{gathered}\)-As:
\(\log _ac=\frac{\log c}{\log a}\)\(\log _{1.06}2=\frac{\log 2}{\log 1.06}=11.89\)Then, after 11.89 or approximately 12 years the money will be 2000.---------------------------To find the amount of money after 10 years you substitute the t in the equation for 10 and evaluate the function:
\(\begin{gathered} f(t)=1000(1.06)^t \\ f(10)=1000(1.06)^{10} \\ f(10)=1000(1.7908)=1790.8 \end{gathered}\)Then, after 10 years the amount of money in the account is $1790.8-----------------------The general equation for a compounded interest is:
\(f(t)=C(1+i)^t\)Where C is the initial deposit
i is the interest (in decimal)
As you have:
\(1+i=1.06\)the interest in decimal will be:
\(\begin{gathered} 1.06-1=i \\ 0.06=i \end{gathered}\)Then, the interest rate is: 6%\(\begin{gathered} i\cdot100 \\ =0.06\cdot100 \\ =6 \end{gathered}\)The graph shows a swimming pool being filled at a rate of 2,000 gallons of water
per hour. How will the graph change if the rate doubles?

Answers
From the presentation of the graph in the question, we can see that the graph would become steeper. Option A
Does the line of the graph become steeper when the rate doubles?When the rate of change of a graph doubles, the line becomes steeper.
The rate of change of a graph is also known as the slope, which is defined as the change in the y-coordinate divided by the change in the x-coordinate between two points on the line. When the rate of change doubles, the change in the y-coordinate for a given change in the x-coordinate also doubles, which means that the line becomes steeper.
Learn more about graph:https://brainly.com/question/17267403
#SPJ1
Please help me so stressed

Answers
6 = 37 degrees
7 = 143 degrees
Why should I probably get my first credit card from the same institution that has my checking and/or savings account?Because building a relationship with a financial institution makes good OA sense You should not. You should get your first card at one of those really cool OB. student websites. A better idea is to pick your credit card company based on which gift I like Oc the best. OD Because local institutions offer better gifts
Answers
I probably get my first credit card from the same institution that has my checking and/or savings account because that is the right thing to do.
What is a credit card?The credit card is a type of card that could be used to pay for utilities. The credit card is a thin plastic card that is issued by a person's financial institution and is recognized for financial transaction.
However, the credit car should be used with caution so that a person do not accumulate a lot of debt on the credit card that could lead to the bankruptcy of the individual that is using the cards in question.
Now, I probably get my first credit card from the same institution that has my checking and/or savings account because that is the right thing to do.
Learn more about credit card:https://brainly.com/question/27350251
#SPJ1
determine the value of x and find measure of both angles

Answers
Given:
m∠1 = 20 - 8x
m∠2 = 30 - 16x
From the image we can see that m∠1 and m∠2 are corresponding angles, and corresponding angles are equal.
Therefore, we have:
m∠1 = m∠2
20 - 8x = 30 - 16x
Let's solve for x:
Add 16x to both sides:
20 - 8x + 16x = 30 - 16x + 16x
20 + 8x = 30
Subtract 20 from both sides:
20 - 20 + 8x = 30 - 20
8x = 10
Divide both sides by 8:
\(\begin{gathered} \frac{8x}{8}=\frac{10}{8} \\ \\ x\text{ = }1.25 \end{gathered}\)x = 1.25
m∠1 = 20 - 8x = 20 - 8(1.25) = 20 - 10 = 10
m∠1 = 10
m∠2 = 30 - 16x = 30 - 16(1.25) = 30 - 20 = 10
m∠2 = 10
ANSWER:
x = 1.25
m∠1 = 10 degrees
m∠2 = 10 degrees
If an investment company pays 6% compounded semiannually, how much will you have 5 years from now if you deposit $900?
How much would you earn if it were simple interest instead of compound interest?
Answers
With compound interest of 6% paid semiannually, a deposit of $900 would result in $1,191.02 after 5 years, while simple interest would earn $270, resulting in a total of $1,170.
To calculate the future value of an investment with compound interest, we can use the following formula:
FV =\(PV * (1 + r/n)^{(n*t)}\)
where FV, PV, r, n and t is the future value, present value, annual interest rate, number of compounding periods per year and number of years respectively.
In this case, the present value (PV) is $900, the annual interest rate (r) is 6%, and the interest is compounded semiannually, so there are 2 compounding periods per year (n=2). The period (t) of investment is 5 years.
Using these values, we can calculate the future value (FV) as follows:
FV = \(\$900 * (1 + 0.06/2)^{(2*5)\)
= \(\$900 * (1.03)^{10\)
= $1,191.02
Therefore, the future value of the investment after 5 years with compound interest would be $1,191.02.
If the interest were simple interest instead of compound interest, the calculation would be simpler. Simple interest is calculated as follows:
I = P x r x t
where I is the interest, P is the principal or present value, r is the interest rate, and t is the time period.
In this case, the interest rate is still 6% and the investment period is still 5 years, but the interest is calculated only on the principal amount of $900. Therefore, the interest earned would be:
I = $900 x 0.06 x 5
= $270
Therefore, the total amount after 5 years with simple interest would be the sum of the principal and the interest earned, which is:
Total = $900 + $270
= $1,170
Therefore, if the interest were simple interest instead of compound interest, the total amount after 5 years would be $1,170, and the interest earned would be $270.
Leaen more about simple interest here:
https://brainly.com/question/30824126
#SPJ1
A computer programmer receives a weekly wage of $1350, and &229.50 is deducted for income tax. Find the percent of the computer programmer’s salary deducted for income tax.
Answers
The percent of the computer programmer’s salary deducted for income tax is 17%.
What is percentage of a number?
A percentage is a ratio or number that can be expressed as a fraction of 100. In order to calculate a percentage of a number, we must divide it by 100 and then multiply the resulting number by 100. The proportion therefore denotes a component per 100. A percentage of one hundred is what is meant by the word "percent."
Given, weekly wage is $1350 and deduction amount for income tax is $229.50.
The percent of deduction is
\(\frac{229.50}{1350} \times 100\\=0.17 \times 100\\=17\)
Therefore, the percent of the computer programmer’s salary deducted for income tax is 17%.
To learn more about percentage from the given link
https://brainly.com/question/843074
#SPJ9
The table gives estimates of the world population, in millions, from 1750 to 2000. (Round your answers to the nearest million.)
Year Population
1750 790
1800 980
1850 1260
1900 1650
1950 2560
2000 6080
(a) Use the exponential model and the population figures for 1750 and 1800 to predict the world population in 1900 and 1950 1900 1950 million people million people
(b) Use the exponential model and the population figures for 1800 and 1850 to predict the world population in 1950 million people
(c) Use the exponential model and the population figures for 1900 and 1950 to predict the world population in 2000 million people
Answers
Answer:
A.) 1508 ; 1870
B.) 2083
C.) 3972
Step-by-step explanation:
General form of an exponential model :
A = A0e^rt
A0 = initial population
A = final population
r = growth rate ; t = time
1)
Using the year 1750 and 1800
Time, t = 1800 - 1750 = 50 years
Initial population = 790
Final population = 980
Let's obtain the growth rate :
980 = 790e^50r
980/790 = e^50r
Take the In of both sides
In(980/790) = 50r
0.2155196 = 50r
r = 0.2155196/50
r = 0.0043103
Using this rate, let predict the population in 1900
t = 1900 - 1750 = 150 years
A = 790e^150*0.0043103
A = 790e^0.6465588
A = 1508.0788 ; 1508 million people
In 1950;
t = 1950 - 1750 = 200
A = 790e^200*0.0043103
A = 790e^0.86206
A = 1870.7467 ; 1870 million people
2.)
Exponential model. For 1800 and 1850
Initial, 1800 = 980
Final, 1850 = 1260
t = 1850 - 1800 = 50
Using the exponential format ; we can obtain the rate :
1260 = 980e^50r
1260/980 = e^50r
Take the In of both sides
In(1260/980) = 50r
0.2513144 = 50r
r = 0.2513144/50
r = 0.0050262
Using the model ; The predicted population in 1950;
In 1950;
t = 1950 - 1800 = 150
A = 980e^150*0.0050262
A = 980e^0.7539432
A = 2082.8571 ; 2083 million people
3.)
1900 1650
1950 2560
t = 1900 - 1950 = 50
Using the exponential format ; we can obtain the rate :
2560 = 1650e^50r
2560/1650 = e^50r
Take the In of both sides
In(2560/1650) = 50r
0.4392319 = 50r
r = 0.4392319/50
r = 0.0087846
Using the model ; The predicted population in 2000;
In 2000;
t = 2000 - 1900 = 100
A = 1650e^100*0.0087846
A = 1650e^0.8784639
A = 3971.8787 ; 3972 million people
Why is cube root of 9 equal to 9 to the one third power question mark (1 point)
9 to the one third power all cubed equals 9 to the one third times 3 power equals 9 to the first power equals 9
9 to the one third power all cubed equals 9 to the one third plus 3 power equals 9 to the first power equals 9
9 to the one third power all cubed equals 9 to the one third divided by 3 power equals 9 to the first power equals 9
9 to the one third power all cubed equals 9 to the one third minus 3 power equals 9 to the first power equals 9
Answers
Answer:
3
Step-by-step explanation:
because 3*3ʕっ•ᴥ•ʔっ(づ。◕‿‿◕。)づ(づ。◕‿‿◕。)づ