Set up the appropriate form of a particular solution y, for the following differential equation, but do not determine the values of the coefficients. y (4) +10y" +9y = 5 sin x + 5 cos 3x Which of the following is the appropriate form of a particular solution yp? O A. yp = (A+BX+Cx? + Dxº) e* OB. Yp = Ax cos x + Bx sin x + Cx cos 3x + Dx sin 3x Oc. Yo = (A + Bx) e*+Csin 3x + Dcos 3X OD. Yp = A cos x +B sin x +C cos 3x + D sin 3x Click to select your answer. BI Type here to search
Answers
The values of these coefficients to set up the appropriate form of the particular solution is A cos(x) + B sin(x) + C cos(3x) + D sin(3x)
The correct option is: Yp = A cos(x) + B sin(x) + C cos(3x) + D sin(3x)
To set up the appropriate form of a particular solution for the given differential equation, we need to first determine the type of the forcing function. The forcing function in this case is 5sinx + 5cos3x, which is a combination of sine and cosine functions with different frequencies. Therefore, the appropriate form of the particular solution would be a combination of sine and cosine functions with coefficients that need to be determined.
The general form of the particular solution can be written as:
yp = A cos(x) + B sin(x) + C cos(3x) + D sin(3x)
Here, A, B, C, and D are the coefficients that need to be determined using the method of undetermined coefficients or variation of parameters. We do not need to determine the values of these coefficients to set up the appropriate form of the particular solution.
Therefore, the correct option is:
D. Yp = A cos(x) + B sin(x) + C cos(3x) + D sin(3x)
To know more about coefficients.
https://brainly.com/question/30845099
#SPJ11
The appropriate form of a particular solution for a differential equation is the form of the solution that matches the form of the non-homogeneous term in the equation. In this case, the non-homogeneous term is 5sin(x) + 5cos(3x), which is a sum of trigonometric functions.
Therefore, the appropriate form of a particular solution would be a linear combination of trigonometric functions, as seen in options B and D. However, we cannot determine the values of the coefficients without further information. It is important to note that the choice of the appropriate form of a particular solution is crucial in finding the complete solution to a differential equation, as it allows us to separate the homogeneous and non-homogeneous parts and solve them separately.
To set up the appropriate form of a particular solution, yp, for the given differential equation y(4) + 10y'' + 9y = 5sinx + 5cos3x, you need to consider the terms on the right-hand side of the equation. Since the right-hand side contains sin(x) and cos(3x) terms, the particular solution should also include these trigonometric functions.
The appropriate form of a particular solution, yp, is: yp = A cos x + B sin x + C cos 3x + D sin 3x (option D). In this form, A, B, C, and D are coefficients to be determined later, and the solution contains the necessary trigonometric functions that match the right-hand side of the given differential equation.
Learn more about trigonometric functions here: brainly.com/question/31962064
#SPJ11
Related Questions
solve for :
a_2=2(a_2+1)
Answers
Step-by-step explanation:
a_2=2a_4+2
a=_2+4_2
a=0
Find the equation of the hyperbola with the following properties. Express your answer in standard form.Foci at (7, 0) and (7, 10)Asymptotes ofy -5 = t;( -7

Answers
Answer:
\(\frac{(y-5)^2}{16}-\frac{(x-7)^2}{9}=1\)
Explanation:
The standard form of an hyperbola is:
\(\frac{(y-k)^2}{a^2}-\frac{(x-h)^2}{b^2}=1\)Where (h, k) are the coordinates of the center.
We are given the asyptotes and the foci.
The foci are (7, 0) and (7, 10)
The y value of the center of the parabola is midway from the two foci. Then, the y-coordinate of the center is 5
The coordinated of the center are (7, 5)
Now, we can use that the form of the asymptotes are:
\(y=k\pm\frac{a}{b}(x-h)\)We have:
\(y-5=\frac{4}{3}(x-7)\)Then:
\(\frac{a}{b}=\frac{4}{3}\)a = 4
b = 3
Now we can write:
\(undefined\)Calculate each Poisson probability: a. P(X = 7), λ = 6 (Round your answer to 4 decimal places.) b. P(X = 11), λ = 12 (Round your answer to 4 decimal places.) c. P(X = 6), λ = 8 (Round your answer to 4 decimal places.)
Answers
P(X = 7), λ = 6: The Poisson probability of X = 7, with a parameter (λ) value of 6, is 0.1446. P(X = 11), λ = 12: The Poisson probability of X = 11, with a parameter (λ) value of 12, is 0.0946. P(X = 6), λ = 8: The Poisson probability of X = 6, with a parameter (λ) value of 8, is 0.1206.
The Poisson probability is used to calculate the probability of a certain number of events occurring in a fixed interval of time or space, given the average rate of occurrence (parameter λ). The formula for Poisson probability is P(X = k) = (e^-λ * λ^k) / k!, where X is the random variable representing the number of events and k is the desired number of events.
To calculate the Poisson probabilities in this case, we substitute the given values of λ and k into the formula. For example, for the first case (a), we have λ = 6 and k = 7: P(X = 7) = (e^-6 * 6^7) / 7!
Using a calculator, we can evaluate this expression to find that the probability is approximately 0.1446. Similarly, for case (b) with λ = 12 and k = 11, and for case (c) with λ = 8 and k = 6, we can apply the same formula to find the respective Poisson probabilities.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
Solve the inequality 4/3|1/4x+3|<4
Ox>-13 and x < -11
Ox<-13 and x > -11
Ox>-24 and x < 0
Ox>-24 and x > 0
Answers
The inequality 4/3|1/4x+3|<4 are Ox>-13 and x < -11 or Ox<-24 and x > 0
How do we determine the absolute values?We can begin by isolating the absolute value on one side of the inequality:
4/3|1/4x+3|<4
|1/4x+3|<3/2
We can then split this inequality into two cases, one for when 1/4x+3 is positive and one for when it is negative:
1/4x+3>0: 1/4x+3>3/2, so multiplying both sides by 4, we get x>-13 and x<-11
1/4x+3<0: 1/4x+3<-3/2, so multiplying both sides by -4, we get x<-24 and x>0
So, the solution is: Ox>-13 and x < -11 or Ox<-24 and x > 0
learn more about inequality: https://brainly.com/question/246993
#SPJ1
which of the following is the solution to the equation x^2-10x+16=0?
1.{2,8}
2.{-4,4}
3.{-16,10}
4. {-8,-2}
Answers
Answer:
1.{2,8}
Step-by-step explanation:
that's my answer
Answer :
1. { 2, 8 }
x² - 10x + 16 = 0
x² - 2x - 8x + 16 = 0
x ( x - 2 ) - 8 ( x - 2 ) = 0
( x - 2 ) ( x - 8 ) = 0
x - 2 = 0
x = 2
x - 8 = 0
x = 8
Therefore,
the solution to the equation x² - 10x + 16 = 0 is { 2, 8 }.
Please help :) thank you



Answers
The value of angle is 1/2 * mGDE=90° and 1/2 * mEFG=90°.
We are given that;
The quadrilateral DEFG
Now,
Since the sum of the arcs EG and GD is equal to the measure of arc ED, we can write:
arc ED = arc EG + arc GD
mEFG + mGDE = 1/2 * arc EG + 1/2 * arc GD
mEFG + mGDE = 1/2 * (arc EG + arc GD)
mEFG + mGDE = 1/2 * arc ED
Since we know that mEFG + mGDE = 180°, we can substitute this into the equation above:
180° = 1/2 * arc ED
arc ED = 360°
So,
1/2 * mGDE = 1/2 * arc GD = (360° - arc ED)/2 = (360° - 180°)/2 = 90°
1/2 * mEFG = 1/2 * arc EG = (360° - arc ED)/2 = (360° - 180°)/2 = 90°
Therefore, by the quadrilaterals answer will be 1/2 * mGDE=90° and 1/2 * mEFG=90°.
Learn more about quadrilaterals here:
https://brainly.com/question/1365755
#SPJ1
how to find the height of a cone given the volume and radius
Answers
Answer:
h = 3V/(πr²)
Step-by-step explanation:
You want to find the height of a cone given the volume and radius.
Volume formulaYou can find the height by using the volume formula and solving it for height.
V = 1/3πr²h
HeightMultiplying by the inverse of the coefficient of h gives ...
3V/(πr²) = h
You can use this formula to find the height from the volume and radius:
h = 3V/(πr²)
<95141404393>
an american society of investors survey found 30% of individual investors have used a discount broker. in a random sample of nine individuals, what is the probability:
Answers
The probability of at most six individuals in the sample having used a discount broker is calculated to be approximately 0.997.
To solve this problem, we need to use the binomial distribution formula. Let X be the number of individuals in the sample who have used a discount broker. Then, X follows a binomial distribution with parameters n = 9 and p = 0.3.
The probability of at most six individuals in the sample having used a discount broker can be calculated as follows:
P(X ≤ 6) = P(X = 0) + P(X = 1) + P(X = 2) + ... + P(X = 6)
Using a binomial probability table or calculator, we can find the individual probabilities and sum them up. Alternatively, we can use a normal approximation to the binomial distribution if the sample size is large enough (np and n(1-p) are both greater than 5).
Using the normal approximation, we have:
mean = np = 9 x 0.3 = 2.7
variance = np(1-p) = 9 x 0.3 x 0.7 = 1.89
standard deviation = √(variance) = 1.374
To standardize the distribution, we calculate the z-score:
z = (6.5 - 2.7) / 1.374 = 2.75
Using a standard normal distribution table or calculator, we find that the probability of a z-score less than or equal to 2.75 is approximately 0.997.
Therefore, the probability of at most six individuals in the sample having used a discount broker is approximately 0.997.
Learn more about Probability :
https://brainly.com/question/18882393
#SPJ4
The complete question is :
What is the probability that in a random sample of nine individual investors, at most six have used a discount broker, given that the American Society of Investors survey found that 30% of individual investors have used a discount broker?
The graph shows the function 7(x) = 2*
What is the value of xwhen x) = 4?
o A. 1
B. 2
C. 0
D. 3
HELP PLEASE

Answers
Answer:
is it 2 because because 4÷2=2
Answer:
B. 2
Step-by-step explanation:
f(x) = 4 and 2 times 2 = 4
Answer for the following questions

Answers
Answer:
H(2) = 7
H(-1) = -2
Step-by-step explanation:
(2)^4-2(2)^2-1
16-2(4)-1
16-8-1
8-1
7
(-1)^4-2(-1)^2-1
1-2(1)-1
-1-1
-2
\(-Xx^{4 }+HX-2x^{2}\)
help me with this question please

Answers
Answer:
N+1
Step-by-step explanation:
It begins with = 2
then n+1=3
then n+2=4 and so on it is n+1
"Matlab
The gradient method was used to find the minimum value of the
function north
f(x,y)=(x^2+y^2−12x−10y+71)^2 Iterations start at the point
(x0,y0)=(2,2.6) and λ=0.002 is used. (The number λ"
Answers
1) The first iteration, n, turns out to be (x1, y1) = ( , ).
2) If the second iteration, n, is (x2, y2) = ( , ).
To find the values of (x1, y1) and (x2, y2), we need additional information or the specific steps of the gradient method applied in MATLAB. The gradient method is an optimization algorithm that iteratively updates the variables based on the gradient of the function. Each iteration involves calculating the gradient, multiplying it by the learning rate (λ), and updating the variables by subtracting the result.
3) After s many iterations (and perhaps changing the value of λ to achieve convergence), it is obtained that the minimum is found at the point (xopt, yopt) = ( , ).
To determine the values of (xopt, yopt), the number of iterations (s) and the specific algorithm steps or convergence criteria need to be provided. The gradient method aims to reach the minimum of the function by iteratively updating the variables until convergence is achieved.
4) The value of the minimum, once the convergence is reached, will be determined by evaluating the function at the point (xopt, yopt). The specific value of the minimum is missing and needs to be provided.
Learn more about gradient method here:
brainly.com/question/28016665
#SPJ11
the complete question is:
Matlab The Gradient Method Was Used To Find The Minimum Value Of The Function North F(X,Y)=(X^2+Y^2−12x−10y+71)^2 Iterations Start At The Point (X0,Y0)=(2,2.6) And Λ=0.002 Is Used. (The Number Λ Is Also Known As The Size Or Step Or Learning Rate.) 1)The First Iteration N Turns Out To Be (X1,Y1)=( , ) 2)If The Second Iteration N Is (X2,Y2)=( ,
Matlab
The gradient method was used to find the minimum value of the function north
f(x,y)=(x^2+y^2−12x−10y+71)^2 Iterations start at the point (x0,y0)=(2,2.6) and λ=0.002 is used. (The number λ is also known as the size or step or learning rate.)
1)The first iteration n turns out to be (x1,y1)=( , )
2)If the second iteration n is (x2,y2)=( , )
3)After s of many iterations (and perhaps change the value of λ to achieve convergence), it is obtained that the minimum is found at the point (xopt,yopt)=( , );
4)Being this minimum=
Each day, Deanne starts working at 10:00 a.m. and Stephanie starts working at noon. At which time each day are the earnings for Deanne equal to the earnings for Stephanie?

Answers
Answer:
Time when both earnings are equal = 5:00 Pm
Step-by-step explanation:
Given:
Total earning of Deanne = 6.50x
Total earning of Stephanie = 9.10(x -2)
Work started at 10:00 am
Find:
Time when both earnings are equal
Computation:
Total earning of Deanne = Total earning of Stephanie
6.50x = 9.10(x - 2)
6.5x = 9.1(x-2)
6.5x = 9.1x - 18.2
9.1x - 6.5x = 18.2
2.6x = 18.2
x = 18.2 / 2.6
x = 7 hour
So,
Time when both earnings are equal = Work started at 10:00 am + 7 hour
Time when both earnings are equal = 5:00 Pm
Frank started the summer with $60 in his account. He
earned $35 working, spent $48 at the beach, spent $24
on movies, spent $50 on new clothes and received $15
for his birthday. What was the final balance of his account
at the end of the summer?
Answers
Answer:
The answer should be 12
Step-by-step explanation
he has 60 in his account already so add 35 and 15 (60+35+15=110) then add 48+24+50 which equals 122. Now subtract 110-122 and you'll get 12. so the answer is 12.
If we are told ab=0, then what can we infer? by the zero product property we know = 0 = 0
Answers
If we are told that ab=0, then we can infer that either a or b (or both) must be equal to 0.
This is because when the product of two numbers is 0, at least one of the numbers must be 0 according to the zero product property.
One of the most crucial concepts for pupils to understand in maths and science is the zero product property.
The greatest educators, mathematicians, and recognized scientists in the fields of physics and chemistry have worked with Vedantu to provide their insights on the subject.
Their suggestions helped us develop materials for your understanding that would make it simple for you to put these ideas into practice.
Know more about zero product property here:
https://brainly.com/question/1626209
#SPJ11
Use the point on the line and the slope of the line to find three additional points that the line passes through. (There is more than one correct answer.) Point / (6,6) Slope / m=0
Answers
Given the point (6,6) on the line and a slope of m = 0, three additional points that the line passes through can be determined. One possible set of points is (6,6), (5,6), (7,6), and (6,0).
When the slope (m) of a line is zero, it indicates that the line is a horizontal line. In this case, the line is parallel to the x-axis and does not have any vertical change. Therefore, the y-coordinate of any point on the line will remain constant.
Given the point (6,6) on the line, we can see that the y-coordinate is 6. Since the slope is zero, the y-coordinate will remain the same for any x-coordinate. Hence, three additional points on the line can be determined by varying the x-coordinate while keeping the y-coordinate constant at 6.
One possible set of points is (6,6), (5,6), (7,6), and (6,0). In this case, we keep the y-coordinate constant at 6 and choose different x-coordinates to form the points. These points lie on the horizontal line passing through (6,6) and have the same y-coordinate.
Learn more about slope here:
https://brainly.com/question/3605446
#SPJ11
find the sum of series 3+5+7+9+.............50 terms
Answers
Answer: 2600
Step-by-step explanation:
\(u_1=3\\u_2=5=3+2=3+2*(2-1)\\u_3=7=5+2=3+2*2=3+2*(3-1)\\u_4=9=3+2*3=3+2*(4-1)\\...\\u_n=3+2*(n-1)\\\\u_{50}=3+2*49=101\\\\\displaystyle \sum_{i=1}^{50}(3+2*i)=\dfrac{3+101}{2} *50=2600\\\)
A survey was conducted on 800 students regarding the number of automobiles in their household. The population mean is 2.7 automobiles with a standard deviation of 0.7.
Which statement is true?
A.
There is a 95% certainty that the sample mean will fall within the interval 2.68 to 2.72.
B.
There is a 95% certainty that the sample mean will fall within the interval 2.67 to 2.73.
C.
There is a 95% certainty that the sample mean will fall within the interval 2.62 to 2.77.
D.
There is a 95% certainty that the sample mean will fall within the interval 2.65 to 2.75.
Answers
What is Shakespeare's most famous love sonnet?
Answers
Answer:
Sonnet 18. One of Shakespeare's best known and most loved sonnets, this reading explains that the stability of love will immortalize a partners beauty and youth. 'Shall I compare three to a summers day? And summers lease hath all too short a date.
Step-by-step explanation:
Which of the following is NOT true of a finite Markov decision process ? You are repeatedly faced with a choice of k different actions that can be taken. The goal is the maximize rewards. The goal is to minimize regret. Each choice's properties and outcomes are fully known at the time of allocation.
Answers
"The goal is to minimize regret" is not true of a finite Markov decision process. A finite Markov decision process is a mathematical model that deals with decision-making problems.
Markov decision processes are used to solve decision-making issues in the fields of economics, finance, operations research, artificial intelligence, and other fields. The following are the properties of a finite Markov decision process: You are repeatedly faced with a choice of k different actions that can be taken. The goal is to maximize rewards. Each choice's properties and outcomes are fully known at the time of allocation. The goal is not to minimize regret. The objective is to maximize rewards or minimize losses. Markov decision processes can be used to model a wide range of decision-making scenarios. They are used to evaluate and optimize plans, ranging from simple scheduling problems to complex resource allocation problems. A Markov decision process is a finite set of states, actions, and rewards, as well as transition probabilities that establish how rewards are allocated in each state. It's a model for decision-making in situations where results are only partly random and partly under the control of a decision-maker.
Note: In a finite Markov decision process, the decision-making agent faces a sequence of decisions that leads to a reward. In contrast to the setting of a reinforcement learning problem, the agent has a specific aim and is not attempting to learn an unknown optimal policy. The decision-making agent knows the transition probabilities and rewards for each state-action pair, allowing it to compute the optimal policy.
To know more about decision process visit :
https://brainly.com/question/1657544
#SPJ11
MatnYou are dealt one card from a 52 card deck. Find the probability that you are dealt a ten or a black card.The probability is I (Type an integer or a fraction. Simplify your answer.)re
Answers
We have to find the probability that you are dealt a ten or a black card.
Out of the 52 card deck, there are 26 black cards.
There are also 4 cards that are tens, but there are 2 cards that are both black and tens.
Then, if we define B: the event of a black card and T: the event of a ten, we can calculate the probability of B or T as:
\(P(B\cup T)=P(B)+P(T)-P(B\cap T)\)Replacing with the values of the probability (success events divided by the total possible events), we can solve this as:
\(\begin{gathered} P(B\cup T)=P(B)+P(T)-P(B\cap T) \\ P(B\cup T)=\frac{21}{52}+\frac{4}{52}-\frac{2}{52} \\ P(B\cup T)=\frac{21+4-2}{52} \\ P(B\cup T)=\frac{23}{52} \end{gathered}\)Answer: the probability of getting a black or a ten is 23/52.
Juan Fuentes is a computer programmer. His annual salary is
$32,190.00. Benefits he receives consist of $1,881.73 in vacation time,
holidays worth $1,287.60, health insurance premiums of
$2,300.00 paid by the employer, Social Security of $1,995.78,
Medicare of $466.76, and unemployment insurance of $541.06.
a. What are the total benefits?
b. What is the rate of benefits?
Answers
In linear equation,$7185.33 is the total benefits.
What are a definition and an example of a linear equation?
An equation with only one variable is referred to as a linear equation in one variable. It has the mathematical formula Ax + B = 0, where A and B can be any two real numbers, and x is an unknowable variable with just one possible value. One such linear equation in one variable is 9x + 78 = 18.the total benefits of Juan Fuentes = $1,881.73 + $2,300.00 + $1,995.78 +
$466.76 + $541.06
= $7185.33
the rate of benefits of Juan Fuentes = $1,287.60
Learn more about linear equation
brainly.com/question/11897796
#SPJ13
A homeowner has 32 feet of fencing to build three sides of a rectangular chicken coup. One side of the chicken coup will be against the barn, so the 32 feet of fence will only be used for three sides.
What are the ideal length and width of the chicken coup that would maximize its area?
Answers
Answer:
The ideal length is 16 feet
The ideal width is 8 feet
Step-by-step explanation:
The given parameters are;
The length of the fencing available to the homeowner = 32 feet
The number of sides of the rectangular chicken coup the fence will be applied = 3 sides
Let L represent the length and W, represent the width
Therefore, we have;
The perimeter of the fence = 2W + L = 32 feet
L = 32 - 2·W
The area is given by, A = Length, L × Width, W
A = (32 - 2·W) × W = 32·W - 2·W²
Differentiating with respect to W and equating to 0 to find the maximum point gives;
dA/dW = d(32·W - 2·W²)/dW = 0
32 - 4·W = 0
4·W = 32
W = 32/4 = 8
W = 8 feet
Given that the sign of the variable in the equation of the derivative is negative, the value we get is the maximum point
The ideal width W = 8 feet
The length, L = 32 - 2·W = 32 - 2 × 8 = 16 feet
Therefore, the ideal length, L = 16 feet.
following and propo Out of 250 coins, 50 are in mint condition. What is the ratio of mint condition coins to the total number of coins?
Answers
Reason:
We have 50 mint condition coins out of 250 total
This forms the ratio 50:250, in which we divide both parts by the GCF 50 to end up with 1:5
The ratio 1:5 tells us that the total is 5 times that of the number of mint condition.
Which expression is equivalent to the expression 5b+16?
3b-6+2b+22
5b-6+b+ 22
2b+4+2b+ 12
7b+3-2b+9
Answers
Answer:
the firsst one trust bruv
Step-by-step explanation:
Option A is correct. The expression that is equivalent to the expression 5b+16 is 3b-6+2b+22
Sum of numbers is a way by which numbers or functions are added together.
According to the given question, we are to find the expression that is equivalent to 5b + 16.
Checking the first option 3b-6+2b+22.
Collecting the like terms
\(= 3b-6+2b+22\\= (3b+2b)-6+22\\=5b+16\\\)
Since the resulting expression is equivalent to 5b+16, this shows that the required expression is 3b-6+2b+22.
Learn more here: https://brainly.com/question/16398026
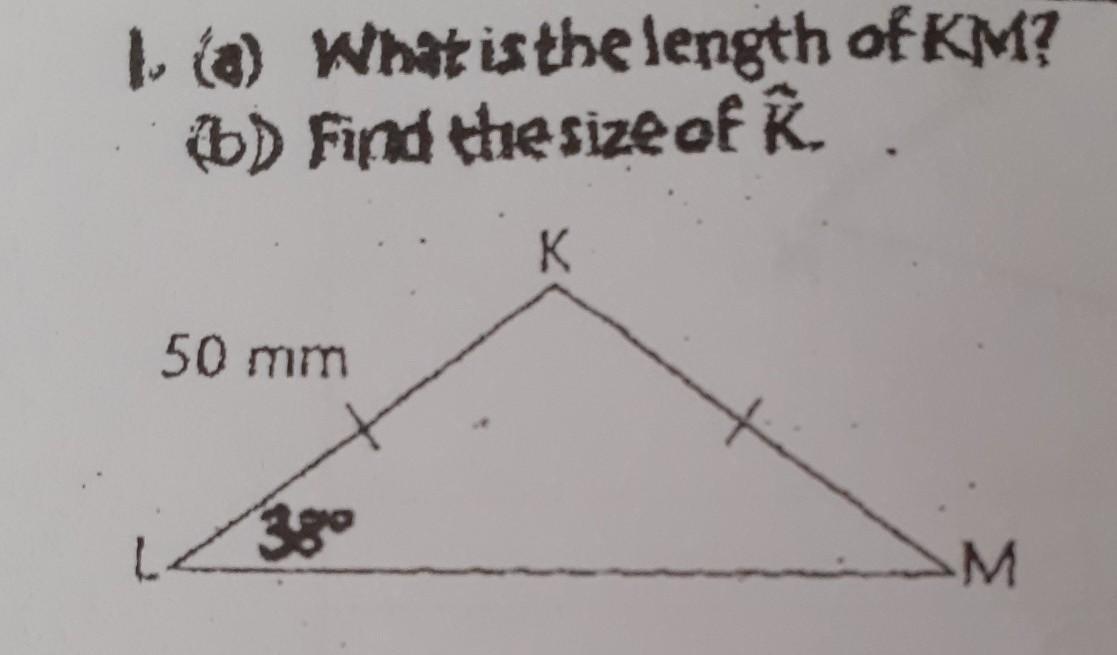
pls help !! answer both 1a and 1b pls
Answers
Answer:
KM = 50 mm , ∠ K = 104°
Step-by-step explanation:
Note that KM = KL = 50mm ( congruent legs )
This indicates the triangle is isosceles with base angles congruent, both 38°
∠ K = 180° - (38 + 38)° = 180° - 76° = 104°
Answer:
So the answer is 398°
Step-by-step explanation:
hope it helps

(1 point) Determine whether the integral is divergent or convergent. If it is convergent, evaluate it. If not, state your answer as "divergent". 147, 4 - = dx (x + 7)3/2
Answers
The integral is convergent.
∫(4 - 147)/(x + 7)^(3/2) dx = -2(143)/(x + 7)^(1/2) + C
To determine the convergence of the given integral:
∫(4 - 147)/(x + 7)^(3/2) dx
We can use the substitution method where we let u = x + 7, then du/dx = 1, and dx = du.
Substituting these values, we get:
∫(4 - 147)/u^(3/2) du
Simplifying the integrand, we get:
∫(-143)/u^(3/2) du
Using the power rule of integration, we get:
-2(143)/u^(1/2) + C
Substituting back u = x + 7, we get:
-2(143)/(x + 7)^(1/2) + C
Since the integral has a finite value, we can say that the integral is convergent. Therefore,
∫(4 - 147)/(x + 7)^(3/2) dx = -2(143)/(x + 7)^(1/2) + C
For more question on convergence
https://brainly.com/question/31385908
#SPJ11
When x is -1.5, what value of y makes the equation true?
Answers
The value of the equation at x = 1, x = -1.5, and x = 8.5 will be 0.5, 7, and -20, respectively.
What is a linear equation?A connection between a number of variables results in a linear model when a graph is displayed. The variable will have a degree of one.
The linear equation is given as,
y = mx + c
Where m is the slope of the line and c is the y-intercept of the line.
The equation is given below.
y = - 3x + 2.5
The value of the equation at x = 1 will be given as,
y = - 3 × (1) + 2.5
y = - 3 + 2.5
y = - 0.5
The value of the equation at x = - 1.5 will be given as,
y = - 3 × (-1.5) + 2.5
y = 4.5 + 2.5
y = 7
The value of the equation at x = 8.5 will be given as,
y = - 3 × (8.5) + 2.5
y = - 22.5+ 2.5
y = - 20
The value of the equation at x = 1, x = -1.5, and x = 8.5 will be 0.5, 7, and -20, respectively.
More about the linear equation link is given below.
brainly.com/question/11897796
#SPJ1
Complete question:

Dan buys a car for £700.
It depreciates at a rate of 5.5% per year.
How much will it be worth in 6 years?
Give your answer to the nearest penny where appropriate
Answers
Answer:
£469
Step-by-step explanation:
Given the following
Original cost of car = £700.
Depreciation rate = 5.5%
Depreciation amount after 1 year = 5.5% * 700
Depreciation amount after 1 year = 0.055 * 700
Depreciation amount after 6 year =6 * 38.5 = £231
Worth after 6 years = £700 - £231
Worth after 6 years = £469
The correct answer is:
£498.53
pls answer along with steps
Thanks

Answers
The angle ACB is tan⁻¹(80/a), the range of tan⁻¹(x) is (0, 90) and the time taken to reach the shore is a/30
Calculating the measure of ACBThe measure of ACB can be calculated using the following tangent trigonometry ratio
tan(ACB) = Opposite/Adjacent
So, we have
tan(β) = 80/a
Take the arc tan of both sides
So, we have
β = tan⁻¹(80/a)
So, the angle is tan⁻¹(80/a)
The range of tan⁻¹(x)Given that the angle is an acute angle
The range of tan⁻¹(x) for acute angles can be found by considering the values of the tangent function for angles between 0 and 90 degrees.
Since tan(0) = 0 and tan(90) is undefined, the tangent function takes on all positive values in this range.
So, the range of tan⁻¹(x) for acute angles is (0, 90) degrees.
The time taken to reach the shoreHere, we have
Distance = a
Speed = 30 km/h
The time taken to reach the shore can be calculated using the formula:
time = distance / speed
Substituting the given values, we get:
time = a / 30 km/h
Simplifying this expression, we get:
time = a / 30 hours
Therefore, the time taken to reach the shore is a/30 hours, where a is the distance to the shore in kilometers.
Read more about bearing distance at
https://brainly.com/question/22719608
#SPJ1