Reviews of call center representatives over the last 8 years showed that 40% of all call center representatives were rated as satisfactory. For a sample of 10 reps selected at random, what is the probability that more than 2 will be rated as satisfactory? a. 0.1672 b. 0.8327 c. 0.1209 d. 0.0123
Answers
The probability that more than 2 out of 10 randomly selected call center representatives will be rated as satisfactory, given a 40% satisfactory rate, is approximately 0.8327.
How can we calculate the probability of having more than 2 satisfactory-rated representatives out of a random sample of 10?To solve this problem, we can use the binomial distribution. The binomial distribution describes the probability of having a certain number of successes in a fixed number of independent Bernoulli trials.
In this case, we have a sample of 10 representatives, and the probability of each representative being rated as satisfactory is 40% or 0.4. We want to find the probability of having more than 2 representatives rated as satisfactory.
The probability mass function (PMF) of the binomial distribution is given by:
\(P(X = k) = C(n, k) * p^k * (1 - p)^(n - k)\)
where:
- P(X = k) is the probability of having exactly k successes
- n is the number of trials (sample size)
- k is the number of successes
- p is the probability of success in a single trial (probability of a representative being rated as satisfactory)
- C(n, k) is the binomial coefficient, calculated as C(n, k) = n! / (k! * (n - k)!)
To find the probability of having more than 2 representatives rated as satisfactory, we need to calculate the probabilities of having 3, 4, 5, ..., 10 successes and sum them up.
Let's calculate the probability:
P(X > 2) = P(X = 3) + P(X = 4) + ... + P(X = 10)
P(X > 2) = ∑[k = 3 to 10] C(10, k) * \((0.4)^k * (1 - 0.4)^(10 - k)\)
We can use software or a calculator to perform this calculation. The result is approximately 0.8327.
Learn more about binomial distribution
brainly.com/question/29163389
#SPJ11
Related Questions
Write only the number answer use the table of values to idetify the value of a for this function

Answers
The value of a for the given function as required in the task content is; 3.
What is the value of a as required in the task content?It follows from the task content that the value of a as in the task content is to be determined;
By convention; the vertex form equation of a quadratic function takes the form;
y = a (x - h)² + k
However, by observing the table, it follows that the vertex of the graph of the function is; ( 0, -48 ).
Therefore, the required equation takes the form;
y = a ( x - 0 )² - 48
Therefore, to determine the value of a using the pair of coordinates; ( -1, -45 ).
By substitution; we have;
-45 = a (-1 - 0)² - 48
-45 + 48 = a
a = 3.
Ultimately, the required value of a as required in the task content is; 3.
Read more on quadratic functions;
https://brainly.com/question/26627449
#SPJ1
george is an engineer in a design company. when the weather is nice he walks to work and sometimes he cycles. in bad weather he takes the bus or he drives. based on past habits there is a 10% probability that george walks, 30% he uses his bike, 20% he drives, and 40% of the time he takes the bus. if george walks, there is a 15% probability of being late to the office. if he cycles there is a 10% chance of being late, a 55% chance of being late if he drives, and a 20% chance of being late if he takes the bus. given that george is late 1 day, what is the probability that he drove?
Answers
The probability that George drove given that he is late is approximately 0.355 or 35.5%.
Let's call the event of George being late "L". The problem is asking for P(Drives | L), which is the probability that George drove given that he is late.
We can use Bayes' theorem to find this probability:
P(Drives | L) = P(L | Drives) * P(Drives) / P(L)
P(L | Drives) is the probability that George is late given that he drove, which is given as 55%.
P(Drives) is the prior probability that George drives, which is given as 20%.
P(L) is the overall probability that George is late, which can be found by summing up the individual probabilities of George being late for each mode of transportation and weighting it by the corresponding prior probability of using that mode of transportation:
P(L) = P(L | Walks) * P(Walks) + P(L | Cycles) * P(Cycles) + P(L | Drives) * P(Drives) + P(L | Bus) * P(Bus)
P(L | Walks) is the probability that George is late given that he walks, which is given as 15%.
P(Cycles) is the prior probability that George cycles, which is given as 30%.
P(Bus) is the prior probability that George takes the bus, which is given as 40%.
P(L | Bus) is the probability that George is late given that he takes the bus, which is given as 20%.
Substituting these values into the formula for P(L) and simplifying:
P(L) = 0.15 * 0.10 + 0.10 * 0.30 + 0.55 * 0.20 + 0.20 * 0.40
= 0.155
Finally, substituting the values for P(L | Drives), P(Drives), and P(L) into the formula for P(Drives | L) and simplifying:
P(Drives | L) = 0.55 * 0.20 / 0.155 = 0.55 / 0.155 = 3.548
For more questions on Bayes' theorem
https://brainly.com/question/29546122
#SPJ4
What fraction of an hour is 32 minutes?
Give your answer in its simplest form
Answers
Answer:
533/1000 already in its simplest form.
How many marginal means would we have if we tested 3 levels of a factor A, 4 levels of a factor B and 2 levels of a factor C?
a. 7
b. 9
c. 24
d. 33
Answers
The number of marginal means would be 24.
How many marginal means would be obtained from testing 3 levels of factor A, 4 levels of factor B, and 2 levels of factor C?In a design that has 3 levels of factor A, 4 levels of factor B, and 2 levels of factor C, the total number of marginal means is 24.
Marginal means are the means for each factor level averaged across the other factors in the design. To calculate the number of marginal means, you simply multiply the number of levels for each factor together.
For example, in this design, there are 3 levels of factor A, 4 levels of factor B, and 2 levels of factor C, so there are 3 x 4 x 2 = 24 marginal means.
Each marginal mean represents the mean score for a particular combination of factor levels, averaged across the other factors in the design.
Learn more about Marginal means
brainly.com/question/31830236
#SPJ11
2 If sin (q) = {(1 – cos x), then lim COS X – 1 x2 = 11 1+0 A. 1 B. 1/2 C. 1/4 D. 0 tan x + sin x – 27x -Y 11 lim 2+0+ sinc - tanr
Answers
To find the limit of cos(x) - 1 / x^2 as x approaches 0, we can use L'Hôpital's rule. This rule allows us to evaluate the limit of an indeterminate form, such as 0/0 or ∞/∞, by taking.
the derivative of the numerator and denominator until we obtain a determinate form.
Taking the derivative of the numerator and , we have:
d/dx(cos(x) - 1) = -sin(x),
d/dx(x^2) = 2x.
Now we can evaluate the limit again:
lim(x→0) [cos(x) - 1 / x^2] = lim(x→0) [-sin(x) / 2x].
We can simplify the limit further:
lim(x→0) [-sin(x) / 2x] = lim(x→0) [-cos(x) / 2].
Finally, evaluating the limit as x approaches 0, we have:
lim(x→0) [-cos(x) / 2] = -cos(0) / 2 = -1/2.
learn more about approaches here :
https://brainly.com/question/30967234
#SPJ11
find the limit. (if the limit is infinite, enter '[infinity]' or '-[infinity]', as appropriate. if the limit does not otherwise exist, enter dne.) lim x→[infinity] x 7x2 4x − 1
Answers
The limit of the expression \(\lim_{x \to 0}\) [(7x² - 70x) / (x² - 100)] which x tends to 0 is equal to 0.
To find the limit of the given expression as x approaches 0,
Simplify the expression and apply algebraic methods.
Let's proceed step by step,
\(\lim_{x \to 0}\) [(7x² - 70x) / (x² - 100)]
First, factorize the numerator and denominator,
\(\lim_{x \to 0}\) [7x(x - 10) / (x + 10)(x - 10)]
Now we can cancel out the common factors of (x - 10) in the numerator and denominator,
\(\lim_{x \to 0}\) [7x / (x + 10)]
Now, substitute x = 0 into the expression,
[7(0) / (0 + 10)] = 0 / 10 = 0
Therefore, the limit of the given expression as x approaches 0 is 0.
learn more about limit here
brainly.com/question/11871065
#SPJ4
The above question is incomplete, the complete question is:
Use properties of limits and algebraic methods to find the limit, if it exists. (If the limit is infinite, enter '∞ ' or ' -∞ ', as appropriate. If the limit does not otherwise exist, enter DNE.)
lim x→0 [( 7x² -70x )/(x² -100)]
WILL GIVE BRAINLIEST

Answers
The time between arrivals of small aircraft at a county airport is exponentially distributed with a mean of one hour. Round the answers to 3 decimal places. (a) What is the probability that more than three aircraft arrive within an hour? Enter your answer in accordance to the item a) of the question statement (b) If 30 separate one-hour intervals are chosen, what is the probability that no interval contains more than three arrivals? Enter your answer in accordance to the item b) of the question statement (c) Determine the length of an interval of time (in hours) such that the probability that no arrivals occur during the interval is 0.27. Enter your answer in accordance to the item c) of the question statement
Answers
a) The probabilities for X = 0, 1, 2, and 3, and then summing them up, we find that P(X > 3) ≈ 0.019. b) The probability of zero successes is approximately 0.430. c) The length of an interval of time is 1.306 hours.
a) The time between arrivals of small aircraft is exponentially distributed with a mean of one hour. To find the probability that more than three aircraft arrive within an hour, we will use the Poisson distribution, where λ (lambda) represents the average number of arrivals per hour, which is 1 in this case. The probability formula is P(X > 3) = 1 - P(X ≤ 3), where X is the number of arrivals. Using the Poisson formula, we get:
P(X > 3) = 1 - [P(X=0) + P(X=1) + P(X=2) + P(X=3)]
Calculating the probabilities for X = 0, 1, 2, and 3, and then summing them up, we find that P(X > 3) ≈ 0.019.
b) To find the probability that no interval contains more than three arrivals in 30 separate one-hour intervals, we can use the binomial distribution. The probability of success (an interval with more than three arrivals) is 0.019 from part a), and the probability of failure (an interval with three or fewer arrivals) is 1 - 0.019 = 0.981. Using the binomial formula with n = 30 (number of intervals) and p = 0.981, we find the probability of zero successes (i.e., no interval with more than three arrivals) is approximately 0.430.
c) To determine the length of an interval of time (in hours) such that the probability that no arrivals occur during the interval is 0.27, we use the exponential distribution formula:
P(T > t) = e^(-λt), where T is the waiting time between arrivals, t is the time interval, and λ is the average number of arrivals per hour (1 in this case).
We want to find the value of t such that P(T > t) = 0.27. So:
0.27 = e^(-1 * t)
Taking the natural logarithm of both sides, we get:
ln(0.27) = -t
Solving for t, we find that t ≈ 1.306 hours.
To learn more about probability click here
brainly.com/question/30034780
#SPJ11
PLZZZ HELP!! 22 pts!!!
Given P(A)=0.5P, (A)=0.5, P(B)=0.24, P(B)=0.24, and P(A and B)=0.2, find the value of P(A or B), rounding to the nearest thousandth, if necessary.
Answers
Work Shown:
P(A or B) = P(A) + P(B) - P(A and B)
P(A or B) = 0.5 + 0.24 - 0.2
P(A or B) = 0.54
a gardener is designing a rectangular planter for a rose garden in front of the administration building on a university campus. the gardener has enough material to build a 300-foot fence to enclose the garden. he also has enough roses to fill a 5,200 square foot planter.
Answers
a. To represent the garden's width, w, in terms of its length, I, we can use the equation: w = 300 - 2I
b. g(l) = l * (300 - 2l) this function gives the area of the rose garden (g) as a function of its length (l)
a. To represent the garden's width, w, in terms of its length, I, we can use the equation:
w = 300 - 2I
The width is equal to the remaining fence length (300 feet) after subtracting twice the length (2I) because the rectangular planter has two equal sides and two equal ends.
b. To define a function g that represents the rose garden's area in terms of its length, l, we can use the equation:
g(l) = l * w
Substituting the expression for the width from part (a), the function becomes:
g(l) = l * (300 - 2l)
This function gives the area of the rose garden (g) as a function of its length (l), taking into account the relationship between length and width.
Learn more about area of rectangle here
https://brainly.com/question/8663941
#SPJ4
complete question is below
A gardener is designing a rectangular planter for a rose garden in front of the administration building on a university campus. The gardener has enough material to build a 300-foot fence to enclose the garden. He also has enough roses to fill a 5,200 square foot planter.
a. Define an expression to represent the garden's width, w, in terms of it length, I.
b. Define a function g to represent the rose garden's area in terms of its length, l.
the R9000 invested at 8%p.a simple interest for 3years show all the steps
Answers
Answer:
To calculate the interest earned on the R9000 invested at 8%p.a simple interest for 3 years, you'll need to use the formula I = Prt.
I = Interest earned
P = Principal amount (R9000)
r = Rate of interest (8% = 0.08)
t = Time (3 years)
Plugging in the values, we get: I = 9000 x 0.08 x 3 = R2160.
Therefore, the interest earned on the R9000 invested at 8%p.a simple interest for 3 years is R2160.
The Probability Density Function For A Uniform Distribution Ranging Between 3 And 5 Is o 2. o Any Positive Value. o 0.5. o Undefined.
Answers
The Probability Density Function (PDF) for a uniform distribution ranging between 3 and 5 is 0.5. Answer is option C.
In a uniform distribution, the probability of a random variable taking any value between the two endpoints of the interval is constant. The probability density function (PDF) of a uniform distribution is a constant value over the range of possible values, and is 0 outside that range. In this case, the PDF for the uniform distribution ranging between 3 and 5 is 0.5, which means that the probability of the random variable taking any value between 3 and 5 is the same, and is equal to 0.5.
The PDF being a constant value of 0.5 implies that the distribution is symmetric, with equal probability of the random variable taking any value between the two endpoints. Thus, option C is answer.
You can learn more about Probability Density Function (PDF) at
https://brainly.com/question/30403935
#SPJ11
The volume of this cone is 643,072 cubic inches. What is the radius of this cone?
Use ≈ 3.14 and round your answer to the nearest hundredth.
Answers
The radius of the cone is 783.84/√h
What is volume of a cone?A cone is the surface traced by a moving straight line (the generatrix) that always passes through a fixed point (the vertex).
Volume is defined as the space occupied within the boundaries of an object in three-dimensional space.
The volume of a cone is expressed as;
V = 1/3πr²h
643072 × 3 = 3.14 × r²h
r²h = 614400
r² = 614400/h
r = 783.84/√h
therefore the radius of the cone is 783.84/√h
learn more about volume of cone from
https://brainly.com/question/1082469
#SPJ1
8(y+4)-2(y-1)=70-3y
solve for y
Answers
Answer:
y = 4
Step-by-step explanation:
8(y + 4) - 2(y - 1) = 70 - 3y ← distribute parenthesis and simplify left side
8y + 32 - 2y + 2 = 70 - 3y
6y + 34 = 70 - 3y ( add 3y to both sides )
9y + 34 = 70 ( subtract 34 from both sides )
9y = 36 ( divide both sides by 9 )
y = 4
what is -2(5x + 1 ) + 3(3x - 9 )
Answers
Answer:
-x - 29
Step-by-step explanation:
-2(5x + 1) + 3(3x - 9) = First, distribute the numbers in the parenthesis
-10x - 2 + 9x - 27 = Then, combine like terms
(-10x + 9x) + (-2 - 27)= Next, distribute the digits
-x - 29
to 4 percent. If Calvin made monthly payments of $220 at the end of each month, how long would it take to pay off his credit card? a. If Calvin made monthly payments of $165 at the end of each month, how long would it take to pay off his credit card? months (Round up to the nearest unit.)
Answers
Rounding up to the nearest unit, it would take Calvin approximately 27 months to pay off his credit card with a monthly payment of $165.
To determine how long it would take Calvin to pay off his credit card, we need to consider the monthly payment amount and the interest rate. Let's calculate the time it would take for two different monthly payment amounts: $220 and $165.
a. Monthly payment of $220:
Let's assume the initial balance on Calvin's credit card is $3,000, and the annual interest rate is 4 percent. To calculate the monthly interest rate, we divide the annual interest rate by 12 (number of months in a year):
Monthly interest rate = 4% / 12 = 0.3333%
Now, we can calculate the time it would take to pay off the credit card using the monthly payment of $220 and the monthly interest rate. We'll use a formula for the number of months required to pay off a loan with fixed monthly payments:
n = -(log(1 - (r * P) / A) / log(1 + r))
Where:
n = number of months
r = monthly interest rate (as a decimal)
P = initial balance
A = monthly payment
Plugging in the values:
n = -(log(1 - (0.003333 * 3000) / 220) / log(1 + 0.003333))
Using a calculator, we can find:
n ≈ 15.34
Rounding up to the nearest unit, it would take Calvin approximately 16 months to pay off his credit card with a monthly payment of $220.
b. Monthly payment of $165:
We can repeat the same calculation using a monthly payment of $165:
n = -(log(1 - (0.003333 * 3000) / 165) / log(1 + 0.003333))
Using a calculator, we find:
n ≈ 26.39
Please note that these calculations assume that Calvin does not make any additional charges on his credit card during the repayment period. Additionally, the interest rate and the balance are assumed to remain constant. In practice, these factors may vary and could affect the actual time required to pay off the credit card balance.
Learn more about interest rate at: brainly.com/question/28236069
#SPJ11
The Florida Everglades welcome about 2×10³ visitors per day. Based on this, about how many visitors come to the Everglades per week?
Answers
Answer:
2000
Step-by-step explanation:
Multiply. Scientific Notation:
2 ⋅ 10-3
Rebekah uses a balance scale to measure the weight of a rock in science class. She finds that its weight is 380 grams. If the actual weight is 363 grams, which of the following is closest to her percent error? Show how you made your choice.
Answers
Answer:
Step-by-step explanation:
4.5 %
Find the area of the rectangle below
length = 11 in
width = 17 in
Answers
Answer:187
Step-by-explanation: width multiply by height
=11 times 17
=187
the picture below shows the shape of a design painted on the side of a building. The design was formed by combining triangles and rectangles.
What is the area of the wall covered by the design?

Answers
Therefore , the solution of the given problem of surface area comes out to be 212 square feet of the wall are therefore covered by the design.
What exactly does an area mean?The total size of the object can be determined by calculating how much room would be required to completely cover its exterior. When choosing a similar product with a cylindrical form, the environment is taken into account. Anything's total dimensions are determined by its surface area. The amount of water that a cuboid can hold depends on the number of sides that link its four trapezoidal shapes.
Here,
We must first determine the area of each individual form before adding them together to determine the portion of the wall that the design covers.
Taking a look at the rectangle first, we can observe that it has the following area:
=> 120 square feet= 10 feet x 12 feet.
=> 40 square feet = (1/2)(10 ft)(8 ft).
Consequently, the two triangles' combined area is:
=> 80 square feet = 2 x 40 square feet.
=> (12 square feet) = (1/2)(6 ft)(4 ft).
The total area of all the shapes is as follows:
=> 212 square feet= 120 square feet, 80 square feet, and 12 square feet.
=> 212 square feet of the wall are therefore covered by the design.
To know more about surface area visit:
https://brainly.com/question/2835293
#SPJ1
Answer: the answer is 261 ^2 ft!
Step-by-step explanation:
Find the square root of the following decimal numbers.
(b) 0.0016
Answers
The square root of the decimal number is √0.0016 = 0.04
How to find the square root of the decimal number?Here we can find the square root of the decimal number:
N = 0.0016
Notice that we can write this number as:
0.0016 = 16*10⁻⁴
Now we can take the square root of that, so we will get:
√(16*10⁻⁴)
We can distribute the square root to get:
√16*√10⁻⁴
These two are easy, we will get:
√16*√10⁻⁴ = 4*10⁻² = 0.04
That is the square root.
Learn more about square roots at:
https://brainly.com/question/428672
#SPJ1
I buy a new TV. The tax rate is 8%. If the total I pay (including tax) is $799.20, how much was the TV before tax
Answers
Answer:
$735.264
Step-by-step explanation:
First, we need to find 8% of the total payment of the TV:
8% of $799.20
\(\frac{8}{100}\) x $799.20
= $63.936
Finally, subtract $63.936 from $799.20:
= $735.264.
Therefore, if I bought a TV and the tax rate is 8% and the total payment of the TV is $799.20, the before tax of the TV is $735.264.
In reference to line items, how many permutations are possible with the letters "ABC"?
Answers
So there are 6 permutations possible with the letters "ABC". These are: ABC, ACB, BAC, BCA, CAB, CBA.
Permutations are a way of arranging objects in a specific order. The number of permutations of a set of n distinct objects is given by n!, where n! denotes the factorial of n.
In the case of the letters "ABC", there are three distinct objects: A, B, and C. Therefore, the number of permutations possible with these letters is:
3! = 3 x 2 x 1 = 6
This means that there are 6 possible ways of arranging the letters "ABC" in a specific order. These permutations are:
ABC
ACB
BAC
BCA
CAB
CBA
To see why there are 6 possible permutations, consider the first position. There are three letters to choose from, so there are three possible choices for the first position. Once the first letter is chosen, there are two letters left to choose from for the second position. Finally, there is only one letter left to choose from for the third position. Therefore, the total number of permutations is:
3 x 2 x 1 = 6
In summary, the number of permutations of a set of n distinct objects is given by n!, and in the case of the letters "ABC", there are 3! = 6 possible permutations: ABC, ACB, BAC, BCA, CAB, and CBA.
To know more about permutation,
https://brainly.com/question/30649574
#SPJ11
A point is chosen uniformly at random from the triangle that is formed by joining the three points (0,0), (0,1), and (1.0). Let X and Y be the coordinates of the point.
(a) What is the joint pdf f(x,y) describing these variables?
(b) What is the probability that X > .5?
(c) What is E(X)?What is E(Y)?
(d) What is Cov(X,Y)?
Answers
(a) The triangle formed by joining the three points (0,0), (0,1), and (1,0) has area 1/2, so the probability density function (PDF) for a point chosen uniformly at random from this triangle is 2 over the area of the triangle, which is 4. Therefore, the joint PDF of X and Y is given by:
f(x,y) = 2, 0 <= x <= 1, 0 <= y <= 1-x
(b) The probability that X > 0.5 is:
P(X > 0.5) = ∫∫_{x>0.5} f(x,y) dx dy
= ∫_{0.5}^1 ∫_{0}^{1-x} 2 dy dx
= ∫_{0.5}^1 2(1-x) dx
= [2x - x^2]_{0.5}^1
= 1/4
Therefore, the probability that X > 0.5 is 1/4.
(c) The marginal PDF of X can be found by integrating the joint PDF over y:
f_X(x) = ∫_{0}^{1-x} 2 dy
= 2(1-x), 0 <= x <= 1
Using this, we can find the expected value of X:
E(X) = ∫_{0}^1 x f_X(x) dx
= ∫_{0}^1 x(2-2x) dx
= [x^2 - x^3/3]_{0}^1
= 2/3
Similarly, the marginal PDF of Y can be found by integrating the joint PDF over x:
f_Y(y) = ∫_{0}^{1-y} 2 dx
= 2(1-y), 0 <= y <= 1
Using this, we can find the expected value of Y:
E(Y) = ∫_{0}^1 y f_Y(y) dy
= ∫_{0}^1 y(2-2y) dy
= [y^2 - y^3/3]_{0}^1
= 1/3
Therefore, E(X) = 2/3 and E(Y) = 1/3.
(d) The covariance of X and Y can be found using the formula:
Cov(X,Y) = E(XY) - E(X)E(Y)
To find E(XY), we can use the joint PDF:
E(XY) = ∫∫_{x,y} xy f(x,y) dx dy
= ∫_{0}^1 ∫_{0}^{1-x} 2xy dy dx
= ∫_{0}^1 (1-x)^2 dx
= [x - 2x^2/3 + x^3/3]_{0}^1
= 1/6
Therefore, the covariance of X and Y is:
Cov(X,Y) = E(XY) - E(X)E(Y)
= 1/6 - (2/3)(1/3)
= -1/18
Therefore, Cov(X,Y) = -1/18.
For more details about covariance click here:
https://brainly.com/question/14300312#
#SPJ11
a) The joint PDF f(x,y) describing the variables X and Y of a point chosen uniformly at random from the triangle that is formed by joining the three points (0,0), (0,1), and (1.0) is given by :The area of the triangle is 1/2 base x height, which in this case is 1/2 x 1 = 1/2.
Therefore, the joint PDF of X and Y is f(x,y) = 2, for 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 and 0 ≤ x+y ≤ 1.
b) What is the probability that X > 0.5?The probability of X > 0.5 is the area of the triangle above the line X = 0.5. Since the height of the triangle is 1 and the base is 0.5, its area is 1/2 x 0.5 x 1 = 1/4.
Therefore, the probability of X > 0.5 is 1/4.
c) What is E(X)? What is E(Y)?E(X)
The marginal PDF of X can be found by integrating the joint PDF over y:
E(X) = ∫∫ x f(x,y) dy dx = ∫∫ 2x dy dx = ∫ (x=0 to 1)
= [x^2 - x^3/3] from 0 to 1 = 2/3
Therefore, E(X) = 2/3
Similarly, E(Y) is given by : E(Y) = ∫∫ y f(x,y) dy = ∫∫ 2y dy dx = ∫ (x=0 to 1) ∫ (y=0 to 1-x) 2y dy dx= ∫ (x=0 to 1) (1-x)^2 dx = [x - x^2/2 + x^3/3] from 0 to 1 = 1/3
Therefore, E(Y) = 1/3
d) What is Cov(X,Y)?
The covariance of X and Y can be found using the formula:
Cov(X.Y)=E(xy)-E(X)E(Y)
Cov(X,Y) = E(XY) - E(X)E(Y) E(XY) is given by : E(XY) = ∫∫ xy f(x,y) dy dx = ∫∫ 2xy dy dx = ∫ (x=0 to 1) ∫ (y=0 to 1-x) 2xy dy dx= ∫ (x=0 to 1) x(1-x)^2 dx = [x^2/2 - x^3/3 + x^4/4] from 0 to 1 = 1/12Therefore, E(XY) = 1/12
Therefore, Cov(X,Y) = E(XY) - E(X)E(Y) = 1/12 - (2/3) x (1/3) = -1/18
To know more about convariance click here:
https://brainly.com/question/14300312#
#SPJ11
What is the range for this set of data?
7, 15, 12
O 3
O 5
O 8
O 12
Answers
Answer:
C/8
Step-by-step explanation:
Because the range is the biggest number subtracted by the lowest number and in our data sat 7,15,and 12 15 is the biggest number and 7 is the smallest so what's 15-7?
8 so C
Have a great day.
I am fairly new to this, and I am having trouble. This is from my ACT prep guide, I will attach another image with the rest of the answer options (total of four answer options *graphs*)


Answers
Given:
\(f(x)=\tan x\)1st graph suits the equation.
Above graph is the final answer.


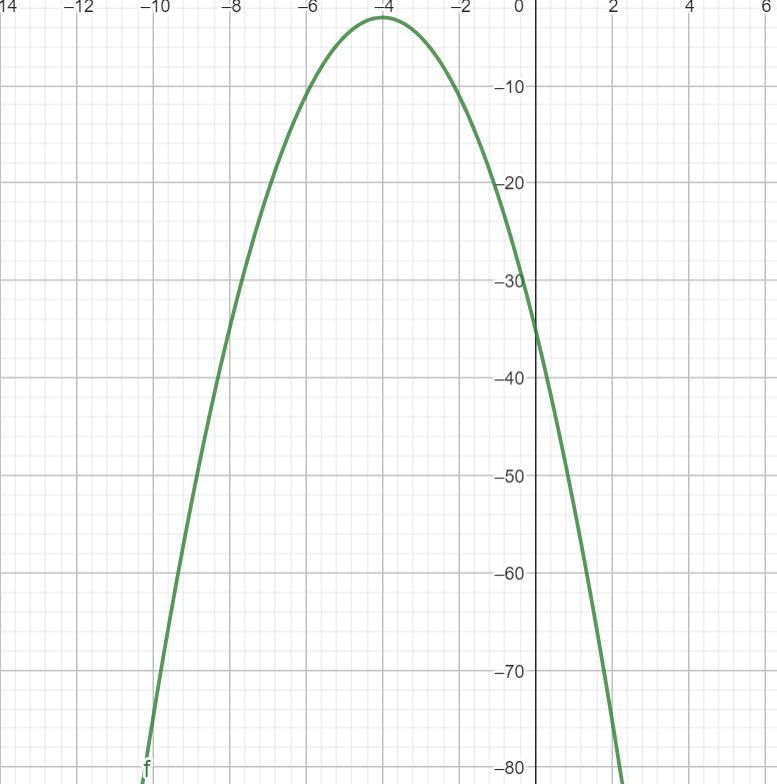
Use the parabola to graph the quadratic function f(x)=-2(x+4)^2-3
Graph the parabola by first plotting its vertex and then plotting a second point on the parabola.
*i’ve been trying to understand this question for so long and when i try to find the answer they don’t make sense!!*

Answers
Given that the directrix is -2 and the vertex is (-4,-3), the graph will be the parabola plotted in the negative quadrant.
What is parabola?Any point on a parabola is at an equal distance from both the focus, a fixed point, and the directrix, a fixed straight line. A parabola is a U-shaped plane curve. Three crucial components make up a parabola: a focus, a directrix, and a vertex. This upward-opening parabola illustrates how all points along its curve will be equally distant from the directrix and the focus.
Here,
The equation of the parabola is,
f(x)=-2(x+4)²-3
a=-2
(h,k)=(-4,-3)
The graph will be the parabola plotted in the negative quadrant as the directrix is -2. and the vertex is (-4,-3).
To know more about parabola,
https://brainly.com/question/21685473?referrer=searchResults
#SPJ1
Systems of equations are often used to model real-life situations. List 2 examples where a system of equations could describe a real-life situation. Elaborate on why you think a system of equations would be useful for each example.
Answers
2 examples where a system of equations could describe a real-life situation are given below.
What is equation?Equation is a physical and mathematical statement that describing physical phenomena and the relationship between different physical quantity typically consist of variable simple presenting physical quantity and then it personal variable may be pointed such as your energy.
1.Modeling a business’s profit: A business can be represented by a system of equations to find the maximum profit. The equations can include the cost of the product, the price of the product, the number of units of the product sold, and other variables such as taxes and shipping costs. By representing the business with a system of equations, a business can optimize the equation to achieve the maximum profit.
2. Modeling the housing market: A system of equations can be used to model the housing market. The equations can include variables such as housing prices, the number of houses on the market, the number of buyers, the supply of housing, and the demand for housing. By using a system of equations, economists can better understand the housing market and make predictions about future trends in the market.
To know more about the equation click-
https://brainly.com/question/26408808
#SPJ1
The endpoints of a diameter of a circle are (7,-4) and (-3,2).
What is the equation of the circle in standard form?
Answers
Answer:
Step-by-step explanation:
-21x - 8y = 0
For a standard normal distribution, find the approximate value of p (z greater-than-or-equal-to negative 1.25). use the portion of the standard normal table below to help answer the question. z probability 0.00 0.5000 0.25 0.5987 1.00 0.8413 1.25 0.8944 1.50 0.9332 1.75 0.9599 11% 39% 61% 89%
Answers
For a standard normal distribution, the approximate value of p
( z≥-1.25 ) is 0.8945.
What is a standard normal distribution?The standard normal distribution is a normal distribution with a mean of zero and a standard deviation of 1. The standard normal distribution is centered at zero and the degree to which a given measurement deviates from the mean is given by the standard deviation.
As we know that Z-score is a numerical measurement that describes a value's relationship to the mean of a group of values.
It is given that z-score≥-1.25
From the standard normal table, the p-value corresponding to z≥-1.25 is
0.8945.
Therefore, For a standard normal distribution, the approximate value of p ( z≥-1.25 ) is 0.8945.
To get more about standard normal distribution visit:
https://brainly.com/question/6758792
Answer:
89%
Step-by-step explanation:
To make it easy. Hope this helps