Pls ans I will beg u I will mark u as brilliant who ever answers by explaining and first only u will give brilliant

Answers
Set 2k+2= 14
2k = 14 - 2
2k = 12
So. k = 6
Andy bought 6 packets of crisps
Related Questions
What is the answer I’m dying here and need to graduate

Answers
We can conclude that -5 is not the domain of f o g.
What is function?A function is a relation between a dependent and independent variable.
Mathematically, we can write → y = f(x) = ax + b.
Given are two functions -
f(x) = 5x - 7
g(x) = √(x - 2)
We can write the functions as -
f o g = f(g{x}) = 5√(x - 2) - 7
Now, refer to the graph attached. At {x} = - 5, the function does not exist. So, we can write that -5 is not the domain of f o g.
Therefore, we can conclude that -5 is not the domain of f o g.
To solve more questions on functions, visit the link-
https://brainly.com/question/29014197
#SPJ9

Solve for x. -3x + 9 = -15
I’m struggling it’s either
8
6
-8
-6
Answers
Hope this helps
Answer:
8 is the answer
Step-by-step explanation:
-3x+9=-15
9+-15=-24 (a plus and a minus always equals a minus)
-3x=-24
-24 divided by -3 = 8
b/4+ 2= -1
help me with this find b
Answers
Answer:
-12
Step-by-step explanation:
Write the equation of each line in slope intercept form. Slope is -6, and (1,-2) is on the line
Answers
See the attached photo for further reference.
Hope this helps! Please make me the brainliest, it’s not necessary but appreciated, I put a lot of effort and research into my answers. Have a good day, stay safe and stay healthy.

What is 4,788 divided by 54?
Answers
Answer:
88.7 rounded and 88.66 not rounded
cos 2x= ___. Check all that apply.
A. sin² x - cos²x
B. 1-2 cos²x
C. 1-2 sin² x
D. 2 cos²x - 1

Answers
Answer:
C and D
Step-by-step explanation:
\(\cos(2x)\\=\cos(x+x)\\=\cos(x)\cos(x)-\sin(x)\sin(x)\\=\cos^2(x)-\sin^2(x)\\=\cos^2(x)-(1-\cos^2(x))\\=2\cos^2(x)-1 \,\,\,\,\,\,\,\,\,\,\leftarrow \text{Option D}\\=2(1-\sin^2(x))-1\\=2-2\sin^2(x)-1\\=1-2\sin^2(x)\,\,\,\,\,\,\,\,\,\,\,\leftarrow \text{Option C}\)
HELP PLEASE URGENT!!!
A Ferris wheel is 50 meters in diameter and boarded from a platform that is 4 meters above the ground. The six o'clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 2 minutes. How many minutes of the ride are spent higher than 38 meters above the ground?
answer in minutes.
Answers
The number of minutes spent higher than 38 meters above the ground on the Ferris wheel ride is approximately 1.0918 minutes.
To solve this problem, we need to determine the angular position of the Ferris wheel when it is 38 meters above the ground.
The Ferris wheel has a diameter of 50 meters, which means its radius is half of that, or 25 meters.
When the Ferris wheel is at its highest point, the radius and the height from the ground are aligned, forming a right triangle.
The height of this right triangle is the sum of the radius (25 meters) and the platform height (4 meters), which equals 29 meters.
To find the angle at which the Ferris wheel is 38 meters above the ground, we can use the inverse sine (arcsine) function.
The formula is:
θ = arcsin(h / r)
where θ is the angle in radians, h is the height above the ground (38 meters), and r is the radius of the Ferris wheel (25 meters).
θ = arcsin(38 / 29) ≈ 1.0918 radians
Now, we know the angle at which the Ferris wheel is 38 meters above the ground.
To calculate the time spent higher than 38 meters, we need to find the fraction of the total revolution that corresponds to this angle.
The Ferris wheel completes one full revolution in 2 minutes, which is equivalent to 2π radians.
Therefore, the fraction of the revolution corresponding to an angle of 1.0918 radians is:
Fraction = θ / (2π) ≈ 1.0918 / (2π)
Finally, we can calculate the time spent higher than 38 meters by multiplying the fraction of the revolution by the total time for one revolution:
Time = Fraction \(\times\) Total time per revolution = (1.0918 / (2π)) \(\times\) 2 minutes
Calculating this expression will give us the answer in minutes.
For similar question on diameter.
https://brainly.com/question/28162977
#SPJ8
two - way frequency tables
Answers
Answer: Two-way frequency tables are especially important because they are often used to analyze survey results. Two-way frequency tables are also called contingency tables. Two-way frequency tables are a visual representation of the possible relationships between two sets of categorical data.
Step-by-step explanation:
The Bremen City School System is opening an all girls academy next school year. The girls choose one top (Green or Yellow), one pant (Khaki or Blue, and one pair of shoes (dress or white), What is the probability of choosing white shoes and a green shirt?
Answers
Answer:
0.25 = 25% probability of choosing white shoes and a green shirt
Step-by-step explanation:
A probability is the number of desired outcomes divided by the number of total outcomes.
In this question:
The probability of choosing a shoe is independent of the shirt. So we find each separate probability, and then multiply them.
Probability of choosing white shoes:
2 shoes option, one of which is white. So
\(P(A) = \frac{1}{2}\)
Probability of choosing a green shirt:
2 shirts options, one of which is green. So
\(P(B) = \frac{1}{2}\)
What is the probability of choosing white shoes and a green shirt?
\(P(A \cap B) = P(A)*P(B) = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}\)
0.25 = 25% probability of choosing white shoes and a green shirt
If you have 32 DVD’s how many more do you need to equal 50
Answers
Let i be the imaginary number √-1. Determine whether the expression a+bi, where a and b are real numbers, represents a real number or a non-real complex number for each case below. Select Real Number or Non-Real Complex number for each case.

Answers
Case 1: a = 0; b = 0 --> Real Number
Case 2: a = 0; b ≠ 0 --> Non-Real Complex Number
Case 3: a ≠ 0; b = 0 --> Real Number
Case 4: a ≠ 0; b ≠ 0 --> Non-Real Complex Number
Understanding Complex NumberFor each case, we can determine whether the expression a + bi represents a real number or a non-real complex number based on the values of a and b.
Case 1: a = 0; b = 0
In this case, both a and b are zero. The expression a + bi simplifies to 0 + 0i, which is equal to 0. Therefore, the expression represents a real number.
Case 2: a = 0; b ≠ 0
Here, a is zero, but b is nonzero. The expression a + bi becomes 0 + bi, where b is a nonzero real number multiplied by the imaginary unit i. Since the expression contains a nonzero imaginary part, it represents a non-real complex number.
Case 3: a ≠ 0; b = 0
In this case, a is nonzero, but b is zero. The expression a + bi simplifies to a + 0i, which is equal to a. As there is no imaginary part in the expression, it represents a real number.
Case 4: a ≠ 0; b ≠ 0
Here, both a and b are nonzero. The expression a + bi contains both a real part (a) and an imaginary part (bi). Thus, it represents a non-real complex number.
Learn more about complex number here:
https://brainly.com/question/5564133
#SPJ1

Evaluate the function f(x) at the given numbers (correct to six decimal places).
f(x) =
x2 − 2x
x2 − 4
,
x = 2.1, 2.05, 2.01, 2.001, 2.0001,
1.9, 1.95, 1.99, 1.999, 1.9999
x f(x)
2.1
0.512195
Correct: Your answer is correct.
2.05
0.5062
Incorrect: Your answer is incorrect.
2.01
0.5012
Incorrect: Your answer is incorrect.
2.001
0.5000
Incorrect: Your answer is incorrect.
2.0001
0.500012
Correct: Your answer is correct.
x f(x)
1.9
0.487179
Correct: Your answer is correct.
1.95
0.493670
Incorrect: Your answer is incorrect.
1.99
0.498746
Incorrect: Your answer is incorrect.
1.999
0.499874
Incorrect: Your answer is incorrect.
1.9999
0.499987
Correct: Your answer is correct.
Answers
Answer:
\(f(2.1) = 0.512195\)
\(f(2.05) = 0.506173\)
\(f(2.01)=0.501247\)
\(f(2.001) = 0.500125\)
\(f(2.0001) = 0.500012\)
\(f(1.9) = 0.487179\)
\(f(1.95) = 0.493671\)
\(f(1.99) = 0.498747\)
\(f(1.999) = 0.499875\)
\(f(1.9999) = 0.499987\)
Step-by-step explanation:
Given
\(f(x) = \frac{x^2 - 2x}{x^2 - 4}\)
Solve for f(x) for all given values of x
First, we need to simplify f(x)
\(f(x) = \frac{x^2 - 2x}{x^2 - 4}\)
\(f(x) = \frac{x(x - 2)}{x^2 - 2^2}\)
\(f(x) = \frac{x(x - 2)}{(x- 2)(x + 2)}\)
\(f(x) = \frac{x}{x + 2}\)
When \(x = 2.1\)
\(f(x) = \frac{x}{x + 2}\)
\(f(2.1) = \frac{2.1}{2.1 + 2}\)
\(f(2.1) = \frac{2.1}{4.1}\)
\(f(2.1) = 0.512195\)
When \(x = 2.05\)
\(f(x) = \frac{x}{x + 2}\)
\(f(2.05) = \frac{2.05}{2 + 2.05}\)
\(f(2.05) = \frac{2.05}{4.05}\)
\(f(2.05) = 0.506173\)
When \(x = 2.01\)
\(f(x) = \frac{x}{x + 2}\)
\(f(2.01)=\frac{2.01}{2.01 +2}\)
\(f(2.01)=\frac{2.01}{4.01}\)
\(f(2.01)=0.501247\)
When \(x = 2.001\)
\(f(x) = \frac{x}{x + 2}\)
\(f(2.001) = \frac{2.001}{2.001 +2}\)
\(f(2.001) = \frac{2.001}{4.001}\)
\(f(2.001) = 0.500125\)
When \(x = 2.0001\)
\(f(x) = \frac{x}{x + 2}\)
\(f(2.0001) = \frac{2.0001}{2.0001 + 2}\)
\(f(2.0001) = \frac{2.0001}{4.0001}\)
\(f(2.0001) = 0.500012\)
When \(x = 1.9\)
\(f(x) = \frac{x}{x + 2}\)
\(f(1.9) = \frac{1.9}{1.9 + 2}\)
\(f(1.9) = \frac{1.9}{3.9}\)
\(f(1.9) = 0.487179\)
When \(x = 1.95\)
\(f(x) = \frac{x}{x + 2}\)
\(f(1.95) = \frac{1.95}{1.95 + 2}\)
\(f(1.95) = \frac{1.95}{3.95}\)
\(f(1.95) = 0.493671\)
When \(x = 1.99\)
\(f(x) = \frac{x}{x + 2}\)
\(f(1.99) = \frac{1.99}{1.99 + 2}\)
\(f(1.99) = \frac{1.99}{3.99}\)
\(f(1.99) = 0.498747\)
\(f(x) = \frac{x}{x + 2}\)
When \(x = 1.999\)
\(f(x) = \frac{x}{x + 2}\)
\(f(1.999) = \frac{1.999}{1.999 + 2}\)
\(f(1.999) = \frac{1.999}{3.999}\)
\(f(1.999) = 0.499875\)
When x = 1.9999
\(f(x) = \frac{x}{x + 2}\)
\(f(1.9999) = \frac{1.9999}{1.9999 + 2}\)
\(f(1.9999) = \frac{1.9999}{3.9999}\)
\(f(1.9999) = 0.499987\)
Note that all values of f(x) are approximated to 6 decimal places
I'll Give brainliest to whoever answers is correct
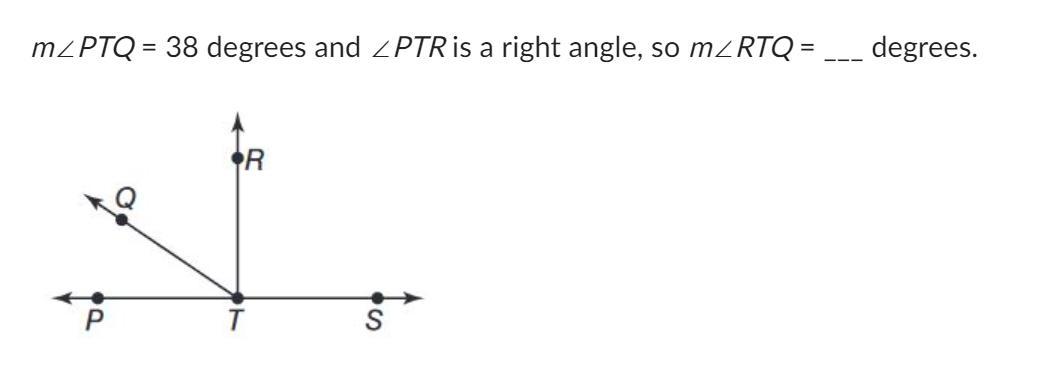
Answers
Answer:
52
Step-by-step explanation:
RTQ is 52 because if PTR is a right angle, right angles equal 90 degrees. So if PTQ is 38 degrees, we subtract 38 from 90 to get RTQ. 90-38 equals 52.
Answer:
52 degrees
Step-by-step explanation:
right angle = 90
90-38=52
So RTQ = 52 degrees
A customer at the mall is shopping for holiday gifts, and is considering having them wrapped He can get them wrapped at the department store, which charges $5 per gift Alternatively, the customer can pay his niece a flat fee of $50 to wrap all of his gifts. If he has a certain number of small packages, it would cost the same amount either way What would be the total cost to have all the gifts wrapped? Write a system of equations, graph them, and type the solution. ____ dollars
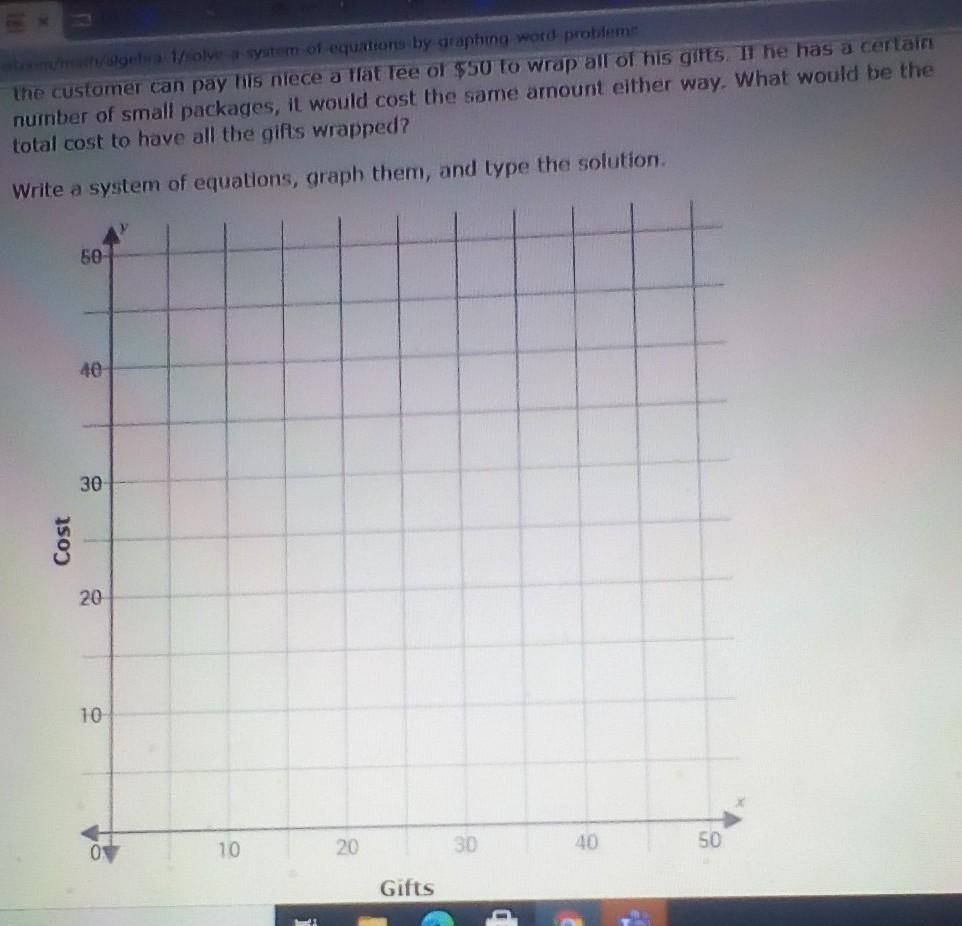
Answers
x is the number of gifts to be wrapped
the cost at the department store is $5 per gift
cost at the department store = 5x
the customer can pay his niece a flat fee of $50
cost of the niece: 50
cost of the niece= cost at department store
5x=50
x=50/5
x=10
y= cost
x=is the number of gifts to be wrapped
the system of equation is
y=5x ---- equation of the department store
y=50 --- equation of the niece
the graph will be
as we can see the two lines intercept when the number of gifts is equal to 10

Write the fraction as a mixed number 10/20
Answers
A chicken farmer started his summer with 6
chickens. By fall, he counted 36 chickens,
and by
winter he counted 216 chickens Which expression
represents the number of chickens he had by
winter?
Need help asap!
Answers
Answer: It is multiplying by 6 each time
A line passes though two points A(-2, 2). B(-1, 2). What is the slope:
Answers
Answer:
The slope is 0
Step-by-step explanation:
Slope = (y2 - y1) / (x2 - x1)
Where the values of x and y are from the known points
Here the points are (-2,2) and (-1,2)
So we have (x1,y1) = (-2,2) and (x2,y2) = (-1,2)
This means, x1 = -2 , x2 = -1 , y1 = 2 and y2 = 2
We now plug these values into the slope formula
Recall slope = (y2 - y1) / (x2 - x1)
==> plug in x1 = -2 , x2 = -2 , y1 = 2, y2 = 2
Slope = (2 - 2) / (-1 - (-2)
==> remove parenthesis
Slope = (2-2) / (-1 + 2)
==> simplify addition and subtraction
Slope = 0 / 1 = 0
can jack built 1/5 of a shed in the same time that kyle can build 5/8 of shed,
how much of a shed will jack have built when kyle finished building 1 shed?
Answers
=============================================================
Explanation:
Let's say the shed comes in 40 equal pieces. Each piece takes the same amount of time to assemble. Why am I picking 40? Because 8*5 = 40.
This will allow us to rewrite the fractions with a common denominator.
1/5 = 8/40 .... multiply top and bottom by 85/8 = 25/40 .... multiply top and bottom by 5So Jack can build 8/40 of the shed in the same amount of time Kyle can build 25/40 of the shed.
Instead of writing fractions (which honestly are a pain to deal with), I'm going to write "8 pieces" and "25 pieces" to represent "8/40" and "25/40" respectively. Just keep in mind that there are 40 pieces total.
So again, Jack can assemble 8 pieces in the time it takes Kyle to assemble 25 pieces.
---------------
The ultimate goal is to have Kyle assemble 40 pieces while Jack puts together some unknown number of pieces (some number between 8 and 40). Let's say it's x.
We can then form this proportion
\(\frac{\text{Jack's initial 8 pieces}}{\text{x pieces}}=\frac{\text{Kyle's initial 25 pieces}}{\text{goal of 40 pieces}}\)
which simplifies or cleans up to
5/x = 25/40
-----------------
Let's solve for x using cross multiplication
8/x = 25/40
8*40 = x*25
320 = 25x
25x = 320
x = 320/25
x = 12.8
So in the time it takes Kyle to assemble all 40 pieces, Jack can put together 12.8 pieces of the shed. However, we can't have Jack put together some fractional piece, because each "piece" is as small as it gets. We can't get any smaller. It would be like saying a fractional part of an atom or a lego block.
So we'll round 12.8 down to 12.
Jack can assemble 12 pieces in the time it takes Kyle to assemble 40 pieces.
Let's then convert this back to fraction form
12 pieces = 12/40 of a shed = 3/10 of a shed.
"A fair die is successively rolled. Let X and Y denote,
respectively, the number of rolls necessary to obtain a 6 and a 5.
Find (a) E[X]; (b) E[X|Y=1]; (c) E[X|Y=5]."
X and Y have a geometric distribution, for part b and c we have E[X|Y = 1] = summation P{X=x, Y=1}/P[Y=1} and E[X|Y = 5] = summation P{X=x, Y=5}/P[Y=5}. Can anyone explain how to find P{X=x, Y=1} and P{X=x, Y=5}?
Answers
The value of the required probabilities are:
(a) E[X] = 6
(b) E[X|Y=1] = 1/36
(c) E[X|Y=5] = 5/36.
To find the values of P{X=x, Y=1} and P{X=x, Y=5}, we need to understand the concept of conditional probability and the properties of geometric distributions.
First, let's recall some properties of geometric distributions:
The probability of success (rolling a specific number on a fair die) in a single trial is denoted by p, and for a fair die, p = 1/6.
The probability of failure (not rolling the specific number) in a single trial is denoted by q, and for a fair die, q = 1 - p = 5/6.
The geometric distribution is the number of trials required to achieve the first success (rolling the specific number) in a sequence of independent trials.
For the random variable X (number of rolls necessary to obtain a 6), X follows a geometric distribution with parameter p = 1/6.
Now, let's find the values of P{X=x, Y=1} and P{X=x, Y=5}.
(a) E[X]:
The expected value of X (denoted as E[X]) for a geometric distribution is given by E[X] = 1/p. For a fair die, p = 1/6, so E[X] = 1 / (1/6) = 6.
(b) E[X|Y=1]:
This represents the expected number of rolls necessary to obtain a 6 given that the first roll resulted in a 5.
To find E[X|Y=1], we need to consider the conditional probability.
The event "Y=1" represents that the first roll resulted in a 5.
The probability of rolling a 6 in the next roll (X=1) given that Y=1 is P{X=1, Y=1}.
Since the rolls are independent, P{X=1, Y=1} = P{X=1} * P{Y=1}.
The probability of rolling a 6 in a single roll (P{X=1}) is 1/6, and the probability of rolling a 5 in a single roll (P{Y=1}) is also 1/6 (since we want the first roll to be a 5).
So, P{X=1, Y=1} = (1/6) * (1/6) = 1/36.
Now, to find E[X|Y=1], we need to sum the products of the number of rolls (x) and the corresponding probabilities for all possible values of x, given that Y=1:
E[X|Y=1] = ∑(x * P{X=x, Y=1})
Since the geometric distribution is defined over all non-negative integers, we need to consider all possible values of x (0, 1, 2, 3, ...).
E[X|Y=1] = (0 * P{X=0, Y=1}) + (1 * P{X=1, Y=1}) + (2 * P{X=2, Y=1}) + ...
Now, we already know that P{X=1, Y=1} = 1/36. For all other values of x, P{X=x, Y=1} = 0 because we cannot have any rolls beyond the first roll when Y=1 (since Y=1 means the first roll was a 5).
So, E[X|Y=1] = (1 * 1/36) + (0 * 0) + (0 * 0) + ... = 1/36.
(c) E[X|Y=5]:
This represents the expected number of rolls necessary to obtain a 6 given that the first roll resulted in a 5 followed by four rolls that resulted in other numbers (not 6).
Similarly to part (b), we need to consider the conditional probability.
The event "Y=5" represents that the first five rolls resulted in numbers other than 6.
The probability of rolling a 6 in the next roll (X=1) given that Y=5 is P{X=1, Y=5}.
Again, since the rolls are independent, P{X=1, Y=5} = P{X=1} * P{Y=5}.
The probability of rolling a 6 in a single roll (P{X=1}) is 1/6, and the probability of rolling a number other than 6 in a single roll (P{Y=5}) is 5/6 (since we want the first five rolls to be numbers other than 6).
So, P{X=1, Y=5} = (1/6) * (5/6) = 5/36.
To find E[X|Y=5], we need to sum the products of the number of rolls (x) and the corresponding probabilities for all possible values of x, given that Y=5:
E[X|Y=5] = ∑(x * P{X=x, Y=5})
Similarly to part (b), for all values of x other than 1, P{X=x, Y=5} = 0 because we cannot have any rolls beyond the first roll when Y=5 (since Y=5 means the first five rolls were other numbers).
So, E[X|Y=5] = (1 * 5/36) + (0 * 0) + (0 * 0) + ... = 5/36.
Hence, The value of the required probabilities are:
(a) E[X] = 6
(b) E[X|Y=1] = 1/36
(c) E[X|Y=5] = 5/36.
To learn more on probability click:
brainly.com/question/11234923
#SPJ12
Find the area of the yellow triangle shown below.

Answers
The height is 12 and the length is 6. After multiplying both they are equal to 72.
Based on the information marked in the diagram

Answers
Answer:
I believe the answer is A. true
Answer:
True
Step-by-step explanation:
What segment is congruent to CD?
Answers
Answer:
we need a picture of the problem
Step-by-step explanation:
If you mix the blue cheese and the cream cheese together, how many cups will there be in all? Write your answer as a reduced fraction in the form a/b. Type your answer with a space between the fraction and whole number.
_______cups?

Answers
this is the working
The answer will be one and three eighth cups
Step-by-step explanation:
hope this helps

An older person is three years older than eight times the age of a younger person. The sum of their age is 21. Find their ages.
Answers
Lets have the younger person be x.
The older person will be 8x + 3.
The sum of their ages is 21, so we can get this equation:
x + (8x+3) = 21
9x+3 = 21
Subtract 3 from both sides
9x = 21
x=3 --> The younger person is 3 years old, and now we can substitute that for the older person (8x+3):
(3 * 8) + 3 = 27
The younger person is 3 years old, and the older person is 27.
whats equivalent to 3:4
Answers
Answer:
6:8
Step-by-step explanation:
if you double the question you get your answer
What is (4×3)÷2+1+2×6
Answers
Answer:
(4×3)÷2+1+2×6
=12÷2+1+2×6
=6+1+2×6
=6+1+12
=19
is the answer
Answer:
19
Step-by-step explanation:
(4*3)/2+1+2*6
=12/2+1+2*6
=6+1+2*6
=6+1+12
=19
Need help to answer question.

Answers
Answer:
0.1
Step-by-step explanation:
There are 1,000 grams in 1 kilogram. Nate is mailing a package that has a mass of 8,000 grams.
He wants to know the mass of the package in kilograms.
1.000
8,000
12,000
grams
kilograms
0
1
12
Multiply or divide?
What is the unit rate. ?
I give brainless!!!!!!!!
Answers
Nate's package is 8 kilograms. This is because, if there are 1,000 grams in 1 kilogram, 8,000/ 1,000= 8 Therefore, the mass of his package is 8 kilograms.
Have a Merry Christmas!
Which is an x-intercept of the continuous function in the
table?
O (-1,0)
O (0, -6)
O (-6, 0)
O (0, -1)

Answers
Answer:
(-1, 0)
Step-by-step explanation:
output = 0 the function’s graph will have an x-intercept
The solution is : (-1, 0), (2, 0), (3, 0) are the x-intercepts of the continuous function f(x).
What are x-intercepts of quadratic function?The zero of the function is where the y-value is zero. The zero of a function is any replacement for the variable that will produce an answer of zero. Graphically, the real zero of a function is where the graph of the function crosses the x‐axis; that is, the real zero of a function is the x‐intercept(s) of the graph of the function.
here, we have,
we know that,
x-intercept of a line is defined by a point where y = 0.
So the point in the form of (x, 0) will be the x-intercept of the given continuous function.
From the table attached,
For x = -1, f(-1) = 0
For x = 2, f(2) = 0
For x = 3, f(3) = 0
Points (-1, 0), (2, 0) and (3, 0) are the x-intercepts of the continuous function f(x).
To learn more on x-intercepts of quadratic function click:
brainly.com/question/28822774
#SPJ7
solve for the missing values in the table below:

Answers
Answer:
The answers to your questions are given below.
Step-by-step explanation:
A. Determination of the length.
Length (cm) = 32
Length (m) =?
Length (mm) =?
I. Determination of the length in m.
100 cm = 1 m
Therefore,
32 cm = 32 × 1 m / 100 cm
32 cm = 0.32 m
II. Determination of the length in mm
1 cm = 10 mm
Therefore,
32 cm = 32 cm × 10 mm / 1 cm
32 cm = 320 mm
B. Determination of the height.
Height (m) = 1.58 m
Height (cm) =?
Height (mm) =?
I. Determination of the height in cm.
1 m = 100 cm
Therefore,
1.58 m = 1.58 m × 100 cm / 1 m
1.58 m = 158 cm
II. Determination of the height in mm
1 m = 1000 mm
Therefore,
1.58 m = 1.58 m × 1000 mm / 1 m
1.58 m = 1580 mm
C. Determination of the width.
Width (mm) = 36 mm
Width (m) =?
Width (cm) =?
I. Determination of the width in m.
1000 mm = 1 m
Therefore,
36 mm = 36 mm × 1 m / 1000 mm
36 mm = 0.036 m
II. Determination of the width in cm
10 mm = 1 cm
Therefore,
36 mm = 36 mm × 1 cm / 10 mm
36 mm = 3.6 cm
D. Determination of the length.
Width (mm) = 105 mm
Width (m) =?
Width (cm) =?
I. Determination of the width in m.
1000 mm = 1 m
Therefore,
105 mm = 105 mm × 1 m / 1000 mm
105 mm = 0.105 m
II. Determination of the width in cm
10 mm = 1 cm
Therefore,
105 mm = 105 mm × 1 cm / 10 mm
105 mm = 10.5 cm
E. Determination of the length.
Length (m) = 2 m
Length (cm) =?
Length (mm) =?
I. Determination of the length in cm.
1 m = 100 cm
Therefore,
2 m = 2 m × 100 cm / 1 m
2 m = 200 cm
II. Determination of the length in mm
1 m = 1000 mm
Therefore,
2 m = 2 m × 1000 mm / 1 m
2 m = 2000 mm
Summary:
Item >>>>>>>> m >>>> cm >>>> mm
A. Lenght >>> 0.32 >> 32 >>>> 320
B. Height >>> 1.58 >> 158 >>>> 1580
C. Width >>> 0.036 >> 3.6 >>>> 36
D. Length >> 0.105 >> 10.5 >>> 105
E. Width >>> 2 >>>>>> 200 >>> 2000