Answers
Answer:
i think Chope its help
C is my answer
Related Questions
Points A(3, 8) and B(–4, 8) are located on a coordinate plane. Graph the pair of points. Then find the distance between them. Use numbers and words to explain your answer.
Answers
Answer:
Step-by-step explanation:
This distance can be calculated by using the distance formula. The distance between two points ( x 1 , y 1 ) and ( x 2 , y 2 ) can be defined as d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 .Jun 2, 2017
Multiply.
3⋅3/5
Enter your answer as an improper fraction, in simplified form, by filling in the boxes.

Answers
Answer:
9/5 or 1 \(\frac{4}{5}\)
Step-by-step explanation:
when multiplying a whole number and a fraction, a fun trick i learned is multiply by the top and divide by the bottom.
3·3=9
9÷5=\(\frac{9}{5}\)
as an improper fraction it would be
1 \(\frac{4}{5}\)
Plz mark as brainliest and rate if i was correct.
Answer:
\(\frac{9}{5}\)
Step-by-step explanation:
3 * 3/5
~Make the 3 improper fraction (note that you can make any whole number a fraction if you put a 1 as the denominator)
3/1 * 3/5
~Multiply both numerators and denominators
9/5
Best of Luck!
The perimeter of a triangle is 54 in. The longest side is 12
in. longer than the medium side, and the medium side is 6
in. more than the shortest side. Find the length of each side
of the triangle.
Answers
The length of the sides of the triangle in discuss as required are; 28 in., 16 in., and 10 in.
What are the lengths of the sides of the triangle?It follows from the task content that the length of the sides of the triangle as described are to be determined.
Let the longest side be; x
The medium side be; x - 12
The smallest side be; (x - 12) - 6.
Therefore, since the perimeter is the sum of all side lengths;
x + x - 12 + x - 12 - 6 = 54
3x = 84
x = 28
Therefore, the longer side is; 28 in.
The medium side is; 28 - 12 = 16 in.
The shortest side is; 16 - 6 = 10 in.
Read more on perimeter of a triangle;
https://brainly.com/question/24299023
#SPJ1
let f(x)=4(1/4)^x+2. what is f(1)? answer in fraction form.
Answers
The value of the function, f(1) is 3. Note that the answer is already in its simplest form and cannot be expressed as a fraction.
First, let's start by understanding what the function f(x) represents. The function f(x) takes an input value x and returns an output value based on a specific rule. In this case, the rule is defined by the equation f(x) = 4(1/4)^x+2.
To find f(1), we need to substitute 1 in place of x in the equation for f(x). So, we get:
f(1) = 4(1/4)^1 + 2
Now, we need to simplify this expression. Recall that any number raised to the power of 1 is just that number itself. So, (1/4)^1 is just 1/4.
Therefore, we can simplify the expression as follows:
f(1) = 4(1/4) + 2
= 1 + 2
= 3
Click the below link, to learn more about the function:
https://brainly.com/question/12431044
#SPJ11
what feature(s) about a relationship can be observed from examining a scatterplot of two quantitative variables x and y?
Answers
By examining a scatterplot, you can gain valuable insights into the relationship between the two quantitative variables x and y, such as direction, strength, form, and outliers.
From examining a scatterplot of two quantitative variables x and y, you can observe the following features about the relationship between the variables:
1. Direction: You can determine whether the relationship between the variables is positive (both variables tend to increase or decrease together) or negative (one variable tends to increase while the other tends to decrease).
2. Strength: You can assess the strength of the relationship by observing how closely the data points are clustered around an imaginary line (e.g., a straight or curved line). A strong relationship has points closely clustered, while a weak relationship has points more scattered.
3. Form: You can identify the form of the relationship, such as linear (points form a straight line) or nonlinear (points form a curve).
4. Outliers: You can detect any outliers, which are data points that do not follow the general pattern of the relationship between the variables.
To learn more about scatterplot: https://brainly.com/question/29785227
#SPJ11
Gina is having a party and wants to spend less than $580. She has already spent $400. The only item left on her list is pizzas, which cost $15 each. How many pizzas, x, can she purchase and stay under her budget? Select the inequality that includes the largest number of pizzas she can purchase and still stay under her budget.
Answers
Answer:
. .
Step-by-step explanation:;
find the absolute maximum value of g(x)=−2x2 x−1 over [−3,5].
Answers
To find the absolute maximum value of the function g(x)=−2x^2/x−1 over the closed interval [−3,5], we will use the Extreme Value Theorem (EVT).EVT states that if a function is continuous over a closed interval, then the function will have an absolute maximum and minimum over that interval.
So, for finding the absolute maximum value of the given function, we will follow these steps:Step 1: Check the function's domain.We know that the denominator of the function g(x) is x - 1, so the function is not defined at x = 1. However, the closed interval we are working with is [-3, 5], which does not include x = 1. Hence, the function is defined over this interval.Step 2: Find the critical points of the functionTo find the critical points, we need to differentiate the function g(x) and equate it to zero:g'(x) = (-4x(x-1) + 2x^2)/(x-1)^2= 2x(3-x)/(x-1)^2=0So, the critical points of g(x) are x = 0 and x = 3.Step 3: Find the end-point values of the functiong(-3) = -2/5, g(5) = -50/9.
To know more about maximum value visit :-
https://brainly.com/question/22562190
#SPJ11
Which of the following is the solution to lx-13 k 18 ?
A. x < 31
B. x < 31 and x > -5
C. X<31 and x < -5
D. X<31 or x > -5
Answers
calculate the volume when the area completely enclosed by the graphs y=x^2 and y= (3/(1 x^3)) is revolved about the x-axis
Answers
The volume enclosed by the two curves when revolved about the x-axis is \(\(\frac{6\pi}{5} \ln 3 - \frac{3\pi}{2} \cdot 3^{\frac{4}{5}}\).\) To find the volume when the area enclosed by the graphs of \(\(y = x^2\)\)and \(\(y = \frac{3}{x^3}\)\) is revolved about the x-axis, we can use the method of cylindrical shells.
First, let's find the points of intersection between the two curves by setting them equal to each other:
\(\[x^2 = \frac{3}{x^3}\]\)
To simplify this equation, we can multiply both sides by \(\(x^3\)\):
\(\[x^5 = 3\]\)
Now, taking the fifth root of both sides:
\(\[x = \sqrt[5]{3}\]\)
So the two curves intersect at \(\(x = \sqrt[5]{3}\)\).
To calculate the volume area enclosed by the graphs of \(\(y = x^2\)\)and \(\(y = \frac{3}{x^3}\)\) is revolved about the x-axis, we need to integrate the circumference of each cylindrical shell multiplied by its height. The height of each shell is the difference in the y-values of the two curves, and the circumference is\(\(2\pi x\)\).
Let's integrate from \(\(x = 0\)\) to \(\(x = \sqrt[5]{3}\)\):
\(\[V = \int_0^{\sqrt[5]{3}} 2\pi x \left(\frac{3}{x^3} - x^2\right) \, dx\]\)
Simplifying this expression:
\(\[V = 2\pi \int_0^{\sqrt[5]{3}} \left(\frac{3}{x} - x^3\right) \, dx\]\)
Integrating each term separately:
\(\[V = 2\pi \left[3 \ln|x| - \frac{x^4}{4}\right]_0^{\sqrt[5]{3}}\]\)
Plugging in the limits of integration:
\(\[V = 2\pi \left[3 \ln|\sqrt[5]{3}| - \frac{\sqrt[5]{3}^4}{4}\right] - 2\pi \left[3 \ln|0| - \frac{0^4}{4}\right]\]\)
Since \(\(\ln|0|\)\)is undefined, the second term on the right side is zero:
\(\[V = 2\pi \left[3 \ln|\sqrt[5]{3}| - \frac{\sqrt[5]{3}^4}{4}\right]\]\)
Simplifying further:
\(\[V = 2\pi \left[3 \ln 3^{\frac{1}{5}} - \frac{3}{4} \cdot 3^{\frac{4}{5}}\right]\]\)
Using the properties of logarithms, we can simplify the first term:
\(\[V = 2\pi \left[3 \cdot \frac{1}{5} \ln 3 - \frac{3}{4} \cdot 3^{\frac{4}{5}}\right]\]\)
\(\[V = \frac{6\pi}{5} \ln 3 - \frac{3\pi}{2} \cdot 3^{\frac{4}{5}}\]\)
So the volume enclosed by the two curves when revolved about the x-axis is \(\(\frac{6\pi}{5} \ln 3 - \frac{3\pi}{2} \cdot 3^{\frac{4}{5}}\).\)
Learn more about area here: https://brainly.com/question/16151549
#SPJ11
Planes the fly at high speeds and low elevations have radar systems that can determine the range of an obstacle and the angle of elevation to the top of the obstacle. The radar of a plane flying at an altitude of 20,000 feet detects a tower that is 25,000 feet away, with an angle of elevation of 1∘. a. How many feet must the plane rise to pass over the tower? The plane must rise at least feet to pass over the tower. Question 2 b. Planes cannot come closer than 1000 feet vertically to any object. At what altitude must the plane fly in order to pass over the tower? The plane must fly at an altitude of at least feet to pass over the tower.
Answers
a) The plane must descend about 19,860.58 feet to pass over the tower. b) To fly 1000 feet above the tower, the plane must fly at an altitude of 1139.42 feet.
a) To find the height of the tower, we can use the tangent function in trigonometry.
Let's call the height of the tower "h".
We know that:
tan(1°) = h / 25000
Solving for h, we get:
h = 25000 * tan(1°)
Using a calculator, we find that:
h ≈ 139.42 feet
So the tower is about 139.42 feet tall.
To pass over the tower, the plane must rise an additional 139.42 - 20,000 = -19,860.58 feet.
That is, the plane must descend about 19,860.58 feet to pass over the tower.
b) To fly 1000 feet above the tower,
The plane must fly at an altitude of 139.42 + 1000 = 1139.42 feet.
Learn more about tangent function here brainly.com/question/22161213
#SPJ4
when finding a minimum in a linear programming problem, it is possible to find more than one minimum value. yes or no
Answers
The statement 'when finding a minimum in a linear programming problem, it is possible to find more than one minimum value' is True.
In this question, we have been given a statement - 'when finding a minimum in a linear programming problem, it is possible to find more than one minimum value.'
We need to state whether it is true or false.
We know that, the minimum value of the objective function Z = ax + by in a linear programming problem can also occur at more than one corner points of the feasible region.
Therefore, when finding a minimum in a linear programming problem, it is possible to find more than one minimum value.
Learn more about linear programming here:
https://brainly.com/question/29405467
#SPJ4
What is the measure of an exterior angle of a regular hexagon?
Enter your answer in the box.
Answers
Answer:
60°
Step-by-step explanation:
each interior angle of a regular hexagon measures 120° (720° divided by 6 sides)
therefore, each exterior angle measures 180-120 = 60°
Roger and Rita each drive at a constant speed between Phoenix and San Diego. Each driver’s distance (miles) is shown for the same elapsed time (hours) of the trip. Who had a head start, and how many miles was the head start?
Answers
If each driver’s distance (miles) is shown for the same elapsed time (hours) of the trip. The person that had a head start is: Rita had a 28-mile head start.
Determining the speedSlope for speed = (y² - y1) / (x² - x1)
Slope for speed = (130 - 65) / (2 - 1)
Slope for speed= 65 / 1
Slope for speed= 65 mph
Determining Roger's starting position if Roger distance is 65.
Hence,
Mile of head start = Slope of speed - Roger distance
Mile of head start = 65 mph - 65 miles
Mile of head start = 0 miles
Rita starting position if Rita distance is 93
Slope for speed = (y² - y1) / (x² - x1)
Slope for speed = (158 - 93) / (2 - 1)
Slope for speed = 65 / 1
Slope for speed = 65 mph
Mile of head start = Slope of speed - Rita distance
Mile of head start = 93 - 65
Mile of head start= 28 miles
Therefore we can conclude that Rita has a head start of 28 miles.
Learn more about speed here : https://brainly.com/question/9623599
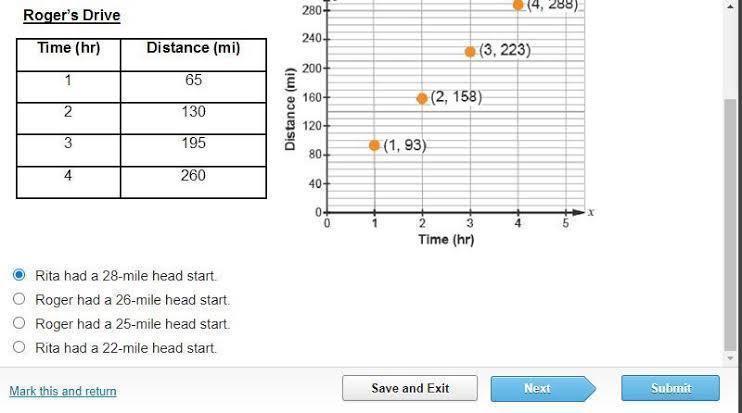
Answer:
Rita had a 28-mile head start.
Step-by-step explanation:
EDGE
Which statement best describes the graph of 2x−5y=−25 and the graph of y=5/2x+5?
Answers
Explanation:
2x - 5y = -25
-5y = -2x - 25
y = (-2/-5)x - 25/-5
y = (2/5)x + 5
y = 5/2x + 5
We can see that their slope is different but have the same y-intercept.
Answer the following questions using the information provided below and the decision tree.
P(s1)=0.56P(s1)=0.56 P(F∣s1)=0.66P(F∣s1)=0.66 P(U∣s2)=0.68P(U∣s2)=0.68
a) What is the expected value of the optimal decision without sample information?
$
For the following questions, do not round P(F) and P(U). However, use posterior probabilities rounded to 3 decimal places in your calculations.
b) If sample information is favourable (F), what is the expected value of the optimal decision?
$
c) If sample information is unfavourable (U), what is the expected value of the optimal decision?
$
Answers
The expected value of the optimal decision without sample information is 78.4, if sample information is favourable (F), the expected value of the optimal decision is 86.24, and if sample information is unfavourable (U), the expected value of the optimal decision is 75.52.
Given information: P(s1) = 0.56P(s1) = 0.56P(F|s1) = 0.66P(F|s1) = 0.66P(U|s2) = 0.68P(U|s2) = 0.68
a) To find the expected value of the optimal decision without sample information, consider the following decision tree: Thus, the expected value of the optimal decision without sample information is: E = 100*0.44 + 70*0.56 = 78.4
b) If sample information is favorable (F), the new decision tree would be as follows: Thus, the expected value of the optimal decision if the sample information is favourable is: E = 100*0.44*0.34 + 140*0.44*0.66 + 70*0.56*0.34 + 40*0.56*0.66 = 86.24
c) If sample information is unfavourable (U), the new decision tree would be as follows: Thus, the expected value of the optimal decision if the sample information is unfavourable is: E = 100*0.44*0.32 + 70*0.44*0.68 + 140*0.56*0.32 + 40*0.56*0.68 = 75.52
To know more about expected value visit:
https://brainly.com/question/13749480
#SPJ11
suppose set a contains 39 elements and the total number elements in either set a or set b is 80. if the sets a and b have 1 elements in common, how many elements are contained in set b?
Answers
Answer:
42 elements-----------------------
Using the formula for the union of two sets:
|A ∪ B| = |A| + |B| - |A ∩ B|where
|A| represents the number of elements in set A, |B| represents the number of elements in set B, and |A ∩ B| represents the number of elements in both sets A and B.We are given that:
|A| = 39|A ∩ B| = 1|A ∪ B| = 80Plugging in the values, we get:
80 = 39 + |B| - 1 |B| = 80 - 38|B| = 42Therefore, set B contains 42 elements.
American ladybugs have an average adult length of 1 cm with a known standard deviation of 0.2 cm. The population of American ladybugs in Raleigh was around 440000 last spring. Assume a normal distribution for the lengths of adult American ladybugs. Your niece asks you what's the probability of a random ladybug in Raleigh being bigger than 1.5 cm. Is it appropriate to calculate this probability? Select one: a. No, because the population distribution is skewed. b. No, because the sample size is less than 30. c. No, because the empirical rule is violated. d. Yes. Clear my choice
Answers
The correct answer is: d. Yes, the probability of a random ladybug in Raleigh being bigger than 1.5 cm and it is appropriate to calculate this probability.
It is appropriate to use a normal distribution to approximate the distribution of ladybug lengths since the sample size is large enough (440000) and the standard deviation is known. We can calculate the z-score for a ladybug with length of 1.5 cm as:
z = (1.5 - 1) / 0.2 = 2.5
Using a standard normal distribution table, we can find the probability of a z-score being greater than 2.5 to be approximately 0.0062. Therefore, the probability of a random ladybug in Raleigh being bigger than 1.5 cm is about 0.0062 or 0.62%.
To know more about probability:
https://brainly.com/question/18237821
#SPJ4
Use the models of f(x) and g(x) to compare the two functions.f(x) = { 3x + 4, x ≤ 1 { 1/3x + 8, x > 1Which comparison is correct?f(-3) < g(-3)f(-3) > g(-3)f(-3) = g(-3)

Answers
The correct option regarding the numeric values of the functions at x = -3 is given as follows:
f(-3) < g(-3).
How to find the numeric value of a function or of an expression?To find the numeric value of a function or of an expression, we replace each instance of the variable in the function or in the expression by the value at which we want to find the numeric value.
At x = -3, the definition of function f(x) for this problem is given as follows:
f(x) = 3x + 4.
(piece-wise function has different definitions depending on the input, -3 is less than 1 hence the first definition is applied).
Hence the numeric value is:
f(-3) = 3(-3) + 4 = -9 + 4 = -5.
From the table, the numeric value of function g(x) at x = -3 is given as follows:
g(-3) = 0.
0 is greater than -5, hence the correct option is given as follows:
f(-3) < g(-3).
A similar problem, also about the numeric values of a function, is given at brainly.com/question/28367050
#SPJ1
Fernando invested money in a 5-yr CD (certificate of deposit) that returned the equivalent of 4.4% simple interest. He invested S2000 less in a 18-month CD that had a 3% simple interest return. If the total amount of interest from these investments was $1102.50, determine how much was invested in ench CD, Fernando invested In the 5-yr CD and 5 in the 18-month CD
Answers
Let x be the amount invested in the 5-yr CD and y be the amount invested in the 18-month CD.
We have the following equations:
0.044x + 0.03(x - 2000) = 1102.50 (total interest equation)
x + (x - 2000) = Total amount invested
Solving this system of equations will give the values of x and y
To determine how much was invested in each CD, we can set up a system of equations. Let x represent the amount invested in the 5-yr CD and y represent the amount invested in the 18-month CD.
The interest earned from the 5-yr CD can be calculated using the formula I = Prt, where I is the interest, P is the principal (amount invested), r is the interest rate, and t is the time in years. In this case, the interest equation for the 5-yr CD is 0.044x.
The interest earned from the 18-month CD can be calculated in the same way, using the formula I = Prt. However, since the time is given in months, we need to convert it to years by dividing by 12. The interest equation for the 18-month CD is 0.03(x - 2000).
The total interest earned from both CDs is $1102.50, so we have the equation 0.044x + 0.03(x - 2000) = 1102.50.
Additionally, the total amount invested is the sum of the amounts invested in each CD, which is x + (x - 2000).
By solving this system of equations, we can determine the values of x and y, representing the amounts invested in each CD. The solution to the system will provide the specific amounts invested in the 5-yr CD and the 18-month CD.
To learn more about Investment
brainly.com/question/29222674
#SPJ11
find the distance traveled by a particle with position ( x, y ) as t varies in the given time interval. compare with the length of the curve?
Answers
The distance traveled by a particle with position (x, y) as t varies in a given time interval can be determined by integrating the speed of the particle with respect to time over that interval. This integration involves calculating the derivatives of x and y with respect to t, representing the rates of change in the x and y coordinates over time. By integrating the speed function, we obtain the total distance traveled by the particle within the given time interval.
To compare this distance with the length of the curve, we need to consider the curve traced by the particle's path in the (x, y) plane. The length of the curve represents the total distance along the curve, taking into account its shape and curvature. Comparing the distance traveled by the particle with the length of the curve allows us to assess if the particle deviates from a straight path or follows a more complex trajectory, providing insights into the particle's motion characteristics.
To learn more about particle motion, click here:
brainly.com/question/1908965
#SPJ11
The distance traveled by a particle with position (x, y) as t varies in a given time interval, we need to integrate the speed of the particle with respect to time over that interval. This will give us the length of the curve traced by the particle's position.
The distance traveled by a particle is determined by integrating its speed over a given time interval. The speed of the particle is the magnitude of its velocity, which can be calculated using the derivatives of the position function.
Let's assume the particle's position is given by a parametric equation x = f(t) and y = g(t), where t represents time. The velocity of the particle can be found by taking the derivatives of f(t) and g(t) with respect to t.
The speed of the particle is then calculated as the magnitude of the velocity vector, which is the square root of the sum of the squares of the derivatives: sqrt((dx/dt)^2 + (dy/dt)^2).
To find the distance traveled by the particle over a specific time interval, we integrate the speed function over that interval with respect to t. This will give us the length of the curve traced by the particle's position.
In summary, to find the distance traveled by a particle, we calculate the speed as the magnitude of its velocity and integrate the speed function over the given time interval. The result will be the length of the curve traced by the particle's position.
to learn more about length click here:
brainly.com/question/17153671
#SPJ11
Simplify the expression
3-(2x+5)
Answers
Answer:
-2x - 2
Step-by-step explanation:
Step 1: Write expression
3 - (2x + 5)
Step 2: Distribute negative
3 - 2x - 5
Step 3: Combine like terms
-2x - 2
JESSIE CAN MAKE 300 PHOTOCOPIES OF A PAGE IN 3 MINUTES. ELSA XANDO THE SAME JOB IN 6 MINUTES. IF BOTH OF THEM WORK TOGETHER, HOW LONG IT WILL TAKE THEM TO DO THE JOB?
Answers
Answer:
elsa can do 150 in 3 minutes.
so together they can do 450 in 3 minutes, or 150 in 1 minute
they would need two minutes
Answer:
4.5 minutes long to do their job.
A wholesaler sells 1 kg of green tea leaves for $8 and 600 g of assam black tea leaves for $7.20. A tea merchant wants to mix these two types of tea leaves to form 100 kg of classic blend. Determine the amount of each type of tea leaves he should order from the wholesaler such that his cost price is $10/kg.
Answers
Answer:
50 kg of green tea leaves and 50 kg of assam black tea leaves.
Step-by-step explanation:
Let x kg be the amount of green tea and y kg be the amount of Assam tea.
x+y=100 (1) [mass]
price for 1 kg of assam tea= 7.20/600×1000g
= $12/kg
total cost= 100×10
= $1000
8x+12y= 1000 (2) [cost]
(1)×8: 8x+8y= 800 (3)
(2)-(3): (8x+12y)-(8x+8y)= 1000-800
4y= 200
y= 50 (4)
sub (4) into (1):
x+50= 100
x= 50
Hi please can you help me this is a new topic and I’m very confused

Answers
Answer: the large jar is cheaper
Step-by-step explanation:
If you divide the £1.54 by 440g and £1.26 by 340g, you'll find which one is cheaper per gram :
1.54/440 = 0.0035
1.26/340 = 0.0037
So, by comparing both prices/gram, you've found that the large jar is cheaper.
Patricia bought 4 apples and 9 bananas for $12. 70. Jose bought 8 apples and 11 bananas for $17. 70 at the same grocery store.
What is the cost of one apple?
Answers
The cost of one apple is $0.70.
Let's assume that the cost of one apple is "a" dollars and the cost of one banana is "b" dollars. We can create two equations based on the information given:
4a + 9b = 12.70 ...(1)
8a + 11b = 17.70 ...(2)
To solve for "a", we can use elimination method by multiplying equation (1) by 8 and equation (2) by -4, so that the coefficients of "a" in both equations will be equal and opposite:
32a + 72b = 101.60
-32a - 44b = -70.80
Adding these two equations, we get:
28b = 30.80
Simplifying and solving for "b", we get:
b = 1.10
Now, we can substitute the value of "b" in equation (1) and solve for "a":
4a + 9(1.10) = 12.70
4a + 9.90 = 12.70
4a = 2.80
a = 0.70
Therefore, the cost of one apple is $0.70.
Learn more about cost ,
https://brainly.com/question/30045916
#SPJ4
Mariam has $560 to spend at a bicycle store for some new a gear
and
biking outfits. Assume all prices listed include tax.
•
She buys a new bicycle for $275.67.
She buys 3 bicycle reflectors for $16.32 each and a pair of bike
gloves for $24.39.
She plans to spend some or all of the money she has left to buy new
biking outfits for $27.40
each.
Write and solve an inequality which can be used to determine x, the
number of outfits Mariam can purchase while staying within her
budget.
Answers
\(\boxed{275.67+3(16.32)+24.39+27.40x \leq 560}\\\\27.40x +349.02 \leq 560\\\\27.40x \leq 210.98\\\\x \leq 7.7\)
Rounding down yields \(\boxed{x \leq 7}\).
Answer:
Step-by-step explanation:
560
Volume (look at the picture)

Answers
Answer:
72
Step-by-step explanation:
volume = l x w x h
4 x 3 x 6
Zeke goes to a skate shop with his friend Tristan. Tristan buys a helmet that costs $28.75. Zeke finds a helmet that is
3
5
of the cost of Tristan's helmet. If Zeke gives the cashier a $20 bill, how much change will he receive?
Answers
Answer:
Zeke will receive $2.75.
Step-by-step explanation:
Helmet cost: (3/5) x 28.75 = $17.25
Gives = $20
20 - 17.25 = 2.75
Original question:
Zeke goes to a skate shop with his friend Tristan. Tristan buys a helmet that costs $28.75. Zeke finds a helmet that is (3/5) of the cost of Tristan's helmet. If Zeke gives the cashier a $20 bill, how much change will he receive?
The function below represents the interest Kristina earns on an investment. Identify the term that represents the amount of money originally invested. f(x) = 5,000(1 + 0.04)x
Answers
Answer:
The amount of money originally invested which is the principal P = 5,000
Step-by-step explanation:
Using the compound interest formula, the return on investment can be represented on the interest function as;
f(x) = P(1+r)^x
Where
P is the principal which is the initial investment.
r = rate Proportion
x = time (number of years)
Comparing to the given function;
f(x) = 5,000(1 + 0.04)^x
We can see that;
Principal P = 5,000
Rate r = 0.04
time = x
The amount of money originally invested which is the principal P = 5,000
Suppose that you decide to buy a car for $57,000, including taxes and license fees. You saved $10,000 for a down payment. The dealer is offering you a choice between two incentives. Incentive A is $5000 off the price of the car, followed by a four-year loan at 6.06%. Incentive B does not have a cash rebate, but provides free financing (no interest) over four years. What is the difference in monthly payments between the two offers? Which incentive is the better deal? Use PMT= P r n 1−1+ r n−nt. The difference in monthly payments between the two offers is $nothing. (Round to the nearest cent as needed.)
Answers
Answer:
Following are the solution to this question:
Step-by-step explanation:
For incentive A
The car value = 57000
Calculating debt\(= 57000 - 10000\)
\(= 47000\)
Calculating the debt value after incentive \(= 47000 - 5000\)
\(= 42000\)
\(PMT = \frac{P(\frac{r}{n})}{(1 - (1 + (\frac{r}{n}))^(-nt))}\)
\(= \frac{42000 \times (\frac{6.06 \%}{12})}{(1-(1+(\frac{6.06 \%}{12}))^{(-12 \times 4)})}\)
\(= \frac{42000 \times (0.00505)}{(1-(1+(0.00505))^{(-48)})}\\\\= \frac{212.1}{(1-(1+(0.00505))^{(-48)})}\\\\=\frac{212.1}{-1.74}\\\\= - 121.89 \ \ or \ \ 121.89\)
For incentive B
The car value = 57000
Calculating the debt value \(= 57000 - 10000\)
\(= 47000\)
Calculating the monthly payment =\(\frac{47000}{(12*4)}\)
\(= \frac{47000}{(48)}\\\\= \frac{47000}{(48)}\\\\=979.166\)
difference:
\(=121.89 - 979.166\\\\ = - 854.276\)
