Answers
Related Questions
Use linear approximation, i.e. the tangent line, to approximate 3√ 125.2 as follows: Let f(x)=√x. The equation of the tangent line to f(x) at x = 125 can be written in the form
y=mx+b
Answers
Using linear approximation, the expression √125.2 can be approximated as approximately 10.02.
How to find linear approximation?To find the equation of the tangent line to the function f(x) = √x at x = 125, determine the slope (m) and the y-intercept (b) of the tangent line.
First, find the slope (m) using the derivative of the function f(x) = √x:
f'(x) = 1 / (2√x)
Evaluate the derivative at x = 125:
f'(125) = 1 / (2√125) = 1 / (2 × 5) = 1/10
Now, find the y-coordinate of the point on the function f(x) at x = 125:
f(125) = √125 = 5
So, the tangent line at x = 125 passes through the point (125, 5) and has a slope of 1/10.
Using the point-slope form of a linear equation, the equation of the tangent line can be written as:
y - 5 = (1/10)(x - 125)
To simplify, multiply through by 10:
10y - 50 = x - 125
Rearranging the equation, express it in the form y = mx + b:
y = (1/10)x - 75/10 + 5
Simplifying further:
y = (1/10)x - 75/10 + 50/10
Combining the terms:
y = (1/10)x - 25/10
Therefore, the equation of the tangent line to f(x) = √x at x = 125 is y = (1/10)x - 25/10.
Now, use this tangent line to approximate the value of √125.2:
Substitute x = 125.2 into the equation:
y = (1/10)(125.2) - 25/10
y = 12.52 - 2.5
y ≈ 10.02
So, using linear approximation, approximate √125.2 as approximately 10.02.
Find out more on linear approximation here: https://brainly.com/question/30403460
#SPJ1
The rocket reaches its maximum height at second(s) after launch. (Simplify your answer.) Save A toy rocket is shot vertically into the air from a launching pad 4 feet above the ground with an initial velocity of 40 feet per second. The height h, in feet, of the rocket above the ground at t seconds after launch is given by the function h(t)= - 16t² + 40t+4. How long will it take the rocket to reach its maximum height? What is the maximum height.
Answers
Answer:
Step-by-step explanation:
The function H(t) = -16t^2 + 64t + 9 is a quadratic function, whose plot is a parabola opened down.
This quadratic function has the maximum at the value of its argument t = -b%2F%282a%29, where "a" is the coefficient at t^2
and "b" is the coefficient at t.
In your case, a= -16, b= 64, so the function gets the maximum at t = -64%2F%282%2A%28-16%29%29 = 2 seconds.
So, the ball gets the maximum height 2 seconds after is hit straight up.
The maximum height is H(t) = -16*2^2 + 64*2 + 9 = 73 ft.
this figure shows Circle O with diameter QS.
mRSQ = 307°, what is the measure of ROQ.
Enter answer in the Box?

Answers
Katherine is 17 years younger than Joe. If Joe is 44 years old, how old is Katherine?
_____years old
Answers
Answer:
Katherine is 27 years old.
Step-by-step explanation:
44-17=27.
Answer:
27
Step-by-step explanation:
44 age of Joe
-17 years younger
______________
27 years of age
help me find the slope please
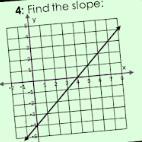
Answers
Answer:
3/4
Step-by-step explanation:
Ok, so I see that the x-intercept is (4,0), while the y-intercept is(-3,0)
Slope is rise/run
Between these two points, the line rose 3 and horizontally went 4 units to the right. Therefore, the slope is 3/4.
Feel free to tell me if I did anything wrong! :)
Also, if you're still confused, I could explain it another way.
Write a function g in terms of f so that the statement is true

Answers
Horizontal changes are often the opposite of what you'd expect to see in the formula.
12:
To shrink/compress horizontally by a factor of 2/3, you need \(g(x) = f(\frac{3}{2}x)\).
Notice we have the reciprocal inside of the function notation.
13:
To translate left 5 units, you have \(g(x) = f( x+5 )\).
Notice we have the opposite sign inside of the function notation.
Amphibian populations are in decline worldwide due to the increasing prevalence of ranavirus infections. Herpetologists (those that study amphibians and reptiles) are especially concerned with how ranavirus infections may be affecting Ozark and eastern hellbender populations.
Suppose both populations of hellbenders are known to have ranavirus infections at a rate of 25%. Suppose a random sample of size 118 is taken of the eastern hellbender population and a random sample of size 177 is taken of the Ozark hellbender population. Every hellbender in each sample is tested for ranavirus, and the sample proportions for each of the two samples are calculated.
Required:
Which of the two sample proportions is more likely to exceed 22% ?
Answers
Answer:
The sample proportion of size 177 is more likely to exceed 22%.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)
Suppose both populations of hellbenders are known to have ranavirus infections at a rate of 25%.
This means that \(\mu = p = 0.25\)
Sample of size 118:
\(n = 118, so \(s = \sqrt{\frac{0.25*0.75}{118}} = 0.0399\)
Probability of sample proportion above 22%.
This is 1 subtracted by the pvalue of Z when X = 0.22. So
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{0.22 - 0.25}{0.0399}\)
\(Z = -0.75\)
\(Z = -0.75\) has a pvalue of 0.2266
1 - 0.2266 = 0.7734
0.7734% probability that a random sample of size 118 exceeds 22%.
Sample of size 177:
\(n = 177, so \(s = \sqrt{\frac{0.25*0.75}{118}} = 0.0325\)
Probability of sample proportion above 22%.
This is 1 subtracted by the pvalue of Z when X = 0.22. So
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{0.22 - 0.25}{0.0325}\)
\(Z = -0.92\)
\(Z = -0.92\) has a pvalue of 0.1788
1 - 0.1788 = 0.8212
0.8212 = 82.12% probability that a random sample of size 177 exceeds 22%.
82.12% > 77.34%, so the sample proportion of size 177 is more likely to exceed 22%.
The sample proportion that is more likely to exceed 22% is; the sample proportion with a sample size of 177
Central Limit Theorem
We are given;
Population proportion; p = 25% = 0.25
Now, in central limit theorem, the formula for standard deviation is;
σ = √(p(1 - p)/n)
For a sample size of 118, we have;
σ = √(0.25(1 - 0.25)/118)
σ = √0.001588983
σ = 0.03986
Similarly, for a sample size of 177, we have;
σ = √(0.25(1 - 0.25)/177)
σ = √0.001059322
σ = 0.032547
Since we want to find which of the two sample proportions will likely exceed 22% which is p₀ = 0.2, we will use the formula;
z = (p₀ - p)/σ
For sample size of 118, we have;
z = (0.22 - 0.25)/0.03986
z = -0.75
From online p-value from z-score calculator, we have;
p-value = 0.7734 or 77.34%
For sample size of 177, we have;
z = (0.22 - 0.25)/0.032547
z = -0.92
From online p-value from z-score calculator, we have;
p-value = 0.8212 or 82.12%
The p-value of the sample of 177 is higher than the p-value for the sample of 118 and so we can say that the sample proportion with a sample size of 177 is more likely to exceed 22%
Read more about Central Limit theorem at; https://brainly.com/question/25800303
Complete the table and find the balance A if $3100 is invested at an annual percentage rate of 4% for 10 years and a compounded n times a year. Complete the table
Answers
The balance for each value of n is calculated by using the formula A = P(1 + r/n) ^nt. The rounded balance values are shown in the last column of the table above.
To complete the table and find the balance A if $3100 is invested at an annual percentage rate of 4% for 10 years and compounded n times a year.
The formula for calculating compound interest is as follows:
A = P(1 + r/n) ^nt,
where P represents the principal investment amount, r is the interest rate, n is the number of times the interest is compounded, t represents the time in years, and A represents the total amount, which includes the principal amount and the interest earned.
The table is given below:
\(\begin{array}{|c|c|c|} \hline \text{n} &
\text{A = P(1 + r/n) }^{nt} &
\text{Balance (rounded to nearest cent)} \\ \hline \text{1} &
\text{3100(1 + 0.04/1)}^{1*10} &
\text{\$4788.03} \\ \hline \text{2} &
\text{3100(1 + 0.04/2)}^{2*10} &
\text{\$4798.76} \\ \hline \text{4} &
\text{3100(1 + 0.04/4)}^{4*10} &
\text{\$4817.46} \\ \hline \text{12} &
\text{3100(1 + 0.04/12)}^{12*10} &
\text{\$4861.94} \\ \hline \end{array}\)
The balance is obtained by substituting the values of P, r, n, and t into the compound interest formula.
In this case, the investment is $3100, the annual interest rate is 4%, the investment is for 10 years, and n is the number of times the interest is compounded.
To learn more about : balance
https://brainly.com/question/23447356
#SPJ8
How much would $200 invested at 4% interest compounded continuously be worth after 5 years ?
Answers
200 x 1.04^5 = 243.33058048
rounded to 243.33
what is the appropriate measure of the missing angle of the triangle shown
Answers
Answer:
it's answer is D. 33°
Let the unknown angle be x Then.
x + 100° + 47° = 180° [ being sum of angles of triangle ]
x + 147° = 180°
x = 180° - 147°
x = 33°
Step-by-step explanation:
if WXYZ is a rectangle, z is located at (-4,-5) and y is located at (-1,-7), find the slope of WZ
Answers
The required slope of WZ is 3/2 for the given situation.
Since WXYZ is a rectangle, WZ is perpendicular to XY, and the slope of WZ is the negative reciprocal of the slope of XY.
The slope of the line is defined as the angle of the line. It is denoted by m
Consider two points on a line—Point 1 and Point 2. Point 1 has coordinates (x₁,y₁) and Point 2 has coordinates (x₂, y₂)
The slope of XY is:
m = (y₂ - y₁)/(x₂ -x₁ ) = (-7 - (-5))/(-1 - (-4)) = -2/3
The negative reciprocal of -2/3 is:
-1/(-2/3) = 3/2
Therefore, the slope of WZ is 3/2.
Learn more about the Slope of the Line here:
brainly.com/question/14511992
#SPJ1
Please help me. Please dont answer if you dont know. i will give brainliest. thankyou, have a great day! :)


Answers
Answer:
1. 3,077.2 cm³
2. 1,808.6 ft³
3. 602.9 in.³
4. 230.8 yd³
5. 191.8 m³
6. 70.3 in.³
Step-by-step explanation:
Recall: Volume of cylinder = πr²h
1. r = 7 cm
h = 20 cm
π = 3.14
Volume = 3.14*7²*20 = 3,077.2 cm³
2. r = 8 ft
h = 9 ft
π = 3.14
Volume = 3.14*8²*9 ≈ 1,808.6 ft³
3. r = ½(8) = 4 in.
h = 12 in.
π = 3.14
Volume = 3.14*4²*12 ≈ 602.9 in.³
4. r = 3½ yd = 3.5 yd
h = 6 yd
π = 3.14
Volume = 3.14*3.5²*6 ≈ 230.8 yd³
5. r = ½(5.3) = 2.65 m
h = 8.7 m
π = 3.14
Volume = 3.14*2.65²*8.7 ≈ 191.8 m³
6. r = 1.9 in.
h = 6.2 in.
π = 3.14
Volume = 3.14*1.9²*6.2 ≈ 70.3 in.³
6.X + 4 using the algebra
tiles.
What tiles need to be added to both sides to remove the
smaller x-coefficient?
What tiles need to be added to both sides to remove the
constant from the right side of the equation?
What is the solution?
Answers
Answer:
i
Step-by-step explanation:
is
coooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooool
Answer:
What tiles need to be added to both sides to remove the smaller x-coefficient?
✔ 5 negative x-tiles
What tiles need to be added to both sides to remove the constant from the right side of the equation?
✔ 4 negative unit tiles
What is the solution?
✔ x = –6
Step-by-step explanation:
3x-9=5+3x
Explain please
Answers
Answer:
x = no solutions
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightEquality Properties
Step-by-step explanation:
Step 1: Define equation
3x - 9 = 5 + 3x
Step 2: Solve for x
Subtract 3x on both sides: -9 ≠ 5Here we see that -9 does not equal 5.
∴ The equation has no solutions.
Star Time:7:30 A.M Elapsed Time:2 hours, 20 minutes End Time is
Answers
Answer:
9:50 A.M.!
Step-by-step explanation:
7 HRS +2 HRS = 9 HRS
30 MINS + 20 MINS = 50 MINS
si ABCD son los vertices de un cuadrado y A(2,2) y C (10,8) 2 vertices opuestos. Hallar los otros dos vertices, dar como respuesta la mayor de las ordenadas
Answers
The area of the square is given as 100 square unit
How to determine the area of square?You should be aware that the square has all its sides equal
The perpendicular from opposite vertices represent distance
The given vertices are
(2,2) and (10,8)
Using the formula for distance between two points
d=√(10-2)²+(8-2)²
d=√8²+6²
d = √64+36
d=√100
This implies that d=10
The area of a square is given as s²
Area = 10²
Atrea = 100 square units
In conclusion, the area of the square is 100 square units
Learn more about area of square on https://brainly.com/question/27683633
#SPJ1
Translated question:
The vertices of a square ABCD are A(2,2) and B(10,8), Find the area of the square

Draw a tape diagram that represent the unknown factor equation o
Answers
The value of x in the equation given as 4x - 3 = 9 will be 3.
How to calculate the valueA tape diagram is a rectangular visual representation that looks like a piece of tape and is widely used to help with addition, subtraction, and multiplication calculations. A divided bar model, fraction strip, length model, or strip diagram are other names for it.
It is a diagram that resembles a piece of tape that is used to show how numbers relate to one another. Also known as length model, fraction strip, bar model, and strip diagrams.
The value of x in 4x - 3 = 9 will be:
4x - 3 = 9
Collect the like terms
4x = 9 + 3
4x = 12
Divide
x = 3
Learn more about tape diagram in:
https://brainly.com/question/26354395
#SPJ1
Draw a tape diagram that represent the unknown factor of x in 4x - 3 = 9

Convert 10 pounds and 12 ounces to ounces.
Answers
Answer: 172 ounces
Step-by-step explanation:
We are given 10 pounds and 12 ounces to convert to ounces.
There are 16 ounces in 1 pound.
We can create a proportion to find out how much ounces 10 pounds is.
10 pounds / x ounces = 1 pound / 16 ounces
We need to solve for x by isolating the variable x.
10/x = 1/16
10 = x/16
10 * 16 = x
160 ounces = x
so 10 pounds is equivalent to 160 ounces. But we are not done yet.
We were asked to convert 10 pounds and 12 ounces.
So add together the ounces to find the total ounces:
160 ounces + 12 ounces = 172 ounces.
Please help I’m very confused on this question.

Answers
While starting salaries have fallen for college graduates in many of the top hiring fields, there is some good news for business undergraduates with concentrations in accounting and finance (Bloomberg Businessweek, July 1, 2010). According to the National Association of Colleges and Employers’ Summer 2010 Salary Survey, accounting graduates commanded the second highest salary at $50,402, followed by finance graduates at $49,703. Let the standard deviation for accounting and finance graduates be $6,000 and $10,000, respectively.
a. What is the probability that 100 randomly selected accounting graduates will average more than $52,000 in salary?
b. What is the probability that 100 randomly selected finance graduates will average more than $52,000 in salary?
c. Comment on the above probabilities.
Answers
Answer:
Step-by-step explanation:
According to the central limit theorem, if independent random samples of size n are repeatedly taken from any population and n is large, the distribution of the sample means will approach a normal distribution. The size of n should be greater than or equal to 30. Given n = 100 for both scenarios, we would apply the formula,
z = (x - µ)/(σ/√n)
a) x is a random variable representing the salaries of accounting graduates. We want to determine P( x > 52000)
From the information given
µ = 50402
σ = 6000
z = (52000 - 50402)/(6000/√100) = 2.66
Looking at the normal distribution table, the probability corresponding to the z score is 0.9961
b) x is a random variable representing the salaries of finance graduates. We want to determine P(x > 52000)
From the information given
µ = 49703
σ = 10000
z = (52000 - 49703)/(10000/√100) = 2.3
Looking at the normal distribution table, the probability corresponding to the z score is 0.9893
c) The probabilities of either jobs paying that amount is high and very close.
y - 7.8= 5.5 I got 2.9 but I want to be sure I understand and took the right steps
Answers
Given the equation:
\(y-7.8=5.5\)You need to solve for "y" in order to find its value. In this case, you need to apply the Addition Property of Equality, which states that, if:
\(a=b\)Then:
\(a+c=b+c\)Therefore, you need to add 7.8 to both sides of the equation in order to solve for "y":
\(\begin{gathered} y-7.8+(7.8)=5.5+(7.8) \\ y=13.3 \end{gathered}\)Hence, the answer is:
\(y=13.3\)Jordan plotted the graph below to show the relationship between the temperature of a city in the number of cups of hot chocolate is sold daily egg in your own words describe the relationship between the temperature of the city and the number cups of hot chocolate sold
Answers
The amount of hot chocolate served daily is inversely correlated with the temperature of the city, with more cups being sold once the temperature is between 40 and 50 F.
Explain about the direct relation?When two variables change in tandem, the relationship is said to be direct. The variable y increases as the variable x increases. A linear relationship denoted by the equation y = kx is directly proportional.
There is a direct correlation between a circle's radius and area, meaning that when the radius is increased or decreased, the area correspondingly changes. If one variable increases while the other declines or vice versa, the relationship between the two variables is inverse.
For given question-
Jordan created the graph below to illustrate the correlation between a city's temperature and the daily sales of hot chocolate.
As we can see that - when the temperature increases the demand for the ice cream also increases which is the direct relation.
Thus, the amount of hot chocolate served daily is inversely correlated with the temperature of the city, with more cups being sold once the temperature is between 40 and 50 F.
Know more about the direct relation
https://brainly.com/question/1266676
#SPJ1
The diagram for the question is attached:

A runner sprinted 103.76 yd to finish a race.
Use the table of facts to find the distance she sprinted in feet.
Round your answer to the nearest tenth.
Answers
Answer:
311.3 feet
Step-by-step explanation:
1 yard = 3 feet
Therefore, 103.76 yards = 311.28 feet (by multiplying 103.76 by 3)
Rounding to the nearest tenth gives us 311.3 feet.
Reflect on the concept of composite and inverse functions. What concepts (only the names) did you need to accommodate these concepts in your mind? What are the simplest composite and inverse functions you can imagine? In your day to day, is there any occurring fact that can be interpreted as composite and inverse functions? What strategy are you using to get the graph of composite and inverse functions?
Answers
The exponential and logarithmic functions are the best examples of inverse functions. I myself never had trouble understanding the idea of composite functions.
As polynomials are just the sum of all the terms with different powers, may they not be referred to as composite functions? I think that exponential functions can often be used to model the population expansion phenomenon. Just concentrate on the simplest examples of these principles if you're having trouble understanding them. If you are familiar with exponents and logarithms, you can use them to better comprehend inverse and composite functions. Graph the individual functions of a composite function if you're having trouble doing so. Then, create coordinate points where the sum of the outputs equals the y-value of the coordinate by adding the outputs of them at specific x-values. By reflecting with respect to the line y = x, you can graph the inverse of a function.
Learn more about inverse functions here
https://brainly.com/question/29497740
#SPJ4
Kaia says the graph does not represent a function. Is Kaia correct? Explain your reasoning.

Answers
Answer: Kaia is not correct
Step-by-step explanation: A function works as long as there is only one 'output' for every 'input', or for every x value, only one y value works. (There can be multiple x values for any y value). If you do the verticle line test on this graph, the line won't pass through two points at the same time anywhere. Therefore, Kaia is incorrect.
Given a graph for the transformation of f(x) in the format g(x) = f(kx), determine the k value.
Two parabolas open up with f of x passing through negative 3 comma negative 3 and g of x passing through negative 1 comma negative 3
k = negative one third
k = one third
k = −3
k = 3
Answers
Given statement solution:- g(x) = \(4(1/4 x^2 + 3/4 x + 9) - 3\)
g(x) = \(x^2 + 3x + 33\) , the Transforming Parabolas correct answer is k = 1/2.
Let's start with the general form of the transformation g(x) = f(kx). To find the value of k, we can use the information given about the graphs of f(x) and g(x).
First, we know that the vertex of the graph of f(x) is at (-3, -3) and that the parabola opens up. This means that the equation of f(x) can be written in the form f(x) = \(a(x + 3)^2\) - 3 for some value of a.
Next, we know that the vertex of the graph of g(x) is at (-1, -3) and that the parabola opens up. Using the transformation equation, we can write g(x) = \(f(kx) = a(kx + 3)^2 - 3.\)
To find the value of k, we need to determine the scaling factor that relates the x-coordinates of the vertex of f(x) to the vertex of g(x). Since the x-coordinate of the vertex of g(x) is 2 units to the right of the vertex of f(x), we have k = 1/2.
Substituting k = 1/2 into the equation for g(x), we get:
g(x) = \(f(kx) = a(1/2 x + 3)^2 - 3\)
Simplifying this equation, we get:
g(x) = \(a(1/4 x^2 + 3x + 9) - 3\)
g(x) = \(1/4 a x^2 + 3/4 a x + 3a + (-3)\)
Comparing this equation to the general form of a parabola, y = \(ax^2 + bx\)+ c, we can see that the coefficient of \(x^2\) is 1/4a, which means that a = 4. Therefore, we have:
g(x) = \(4(1/4 x^2 + 3/4 x + 9) - 3\)
g(x) = \(x^2 + 3x + 33\)
So the Transforming Parabolas correct answer is k = 1/2.
For such more questions on Transforming Parabolas
https://brainly.com/question/17069644
#SPJ11
Can someone help me? I’ll reward points + brainalist (btw only need help with number 13)

Answers
Which of the following statements with respect to political risk is true?
Oa. Political risk premiums are added to the required rate of return to adjust for political risks.
b. Companies cannot take any steps to reduce the potential from loss from expropriation since a foreign
government is involved.
Oc. The risk of expropriation of U.S. assets abroad is high even in traditionally friendly and stable countries.
Od. A company can reduce political risk by structuring operations so that the subsidiary has value only as a part of the
integrated corporate system.
Answers
This statement is true. Political risk is the risk of loss in an investment due to political instability or changes in government policy. Companies can adjust for the potential impact of political risk by adding a political risk premium to their required rate of return. This premium compensates investors for the additional risk associated with the investment due to political factors. The size of the premium will depend on the specific country, the nature of the investment, and the perceived level of political risk. Companies can also take steps to reduce political risk, such as diversifying their operations, investing in political risk insurance, or structuring operations to minimize the value of a subsidiary that might be subject to expropriation.
a number has the digits 2, 5, and 4. To the nearest 100, the number rounds to 200. What is the number?
Answers
Answer:
245
Step-by-step explanation:
if you're rounding to the nearest 100, 245 would be the only one that would round to 200. if it were 250 or above, it would round to 300, so 245 is the only one that would round to 200 because 245 is less than 250
Work out the volume of yhe cone answer to 3 sig fig

Answers
1/3*22/7*3.5*12.5/2*12/2
137.5cm3
