median home price in the west fell from 203400 to 192300 find the percent decrease
Answers
Answer:
Step-by-step explanation:
I took your points looooser hahahaha
Related Questions
14 The straight line, L, has the equation y = 5 - 2x
Write down
(a) the co-ordinates of the point where the line crosses the y-axis,
Answer
Answers
Answer:
When it crosses y-axis it means that x coordinate must be 0 so let substitute 0 to x, y=5-2*0
So coordinates are [0,5]
Maja manages a community garden which has rectangular garden plots that are 15 ft by 10 ft. She wants to add a uniform path around the garden plot so that the combined area of the path is 350 square feet. How wide, in feet, should the path be?
Answers
The path should be 6.38 feet wide
Let x be the width of the path.
Since the rectangular plot has an area with dimensions 15 ft by 10 ft, we add x to each dimension to give the dimensions of the rectangular plot plus uniform path.
So, the dimensions are 15 + x by 10 + x respectively.
So, the area of the rectangular plot plus uniform path is A
A = (15 + x)(10 + x)
Since the combined area of the path is 350 square feet, A = 350 ft²
So, (15 + x)(10 + x) = 350
Expanding the brackets, we have
150 + 15x + 10x + x² = 350
x² + 25x + 150 = 350
x² + 25x + 150 - 350 = 0
x² + 25x - 200 = 0
Using the quadratic formula, we find x, the width of the path
So,
\(x = \frac{-25 +/-\sqrt{25^{2} - 4X1 X (-200)} }{2 X1 } \\x = \frac{-25 +/-\sqrt{625 + 800)} }{2}\\x = \frac{-25 +/-\sqrt{1425} }{2}\\x = \frac{-25 +/-37.75 }{2}\\x = \frac{-25 + 37.75 }{2} or x = \frac{-25 - 37.75 }{2}\\x = \frac{12.75 }{2} or x = \frac{-62.75 }{2}\\x = 6.375 or x = -31.375\)
Since x cannot be negative, we choose the positive answer.
x = 6.375 ft
x ≅ 6.38 ft
So, the path should be 6.38 feet wide
Learn more about width of a path here:
https://brainly.com/question/15382035
Answer:5
Step-by-step explanation:
Let x represent the width of the path. Then the dimensions of the combined garden and path are 15+2x and 10+2x.
(15+2x)(10+2x)-15(10)=350
Simplify the left side.
150+30x+20x+4x^2-150=350
Combine like terms and set one side to zero.
4x^2+50x-350=0
Factor out the common factor, 2.
2(2x^2+25x-175)=0
Factor the resulting trinomial.
2(2x+35)(x-5)=0
Set each factor equal to zero and solve.
2x+35=0\rightarrow x=-35/2 or x-5=0\rightarrow x=5
The only solution that makes sense in this context is 5. Therefore, the path should be 5 ft wide.
Sorting algorithms no unread replies.no replies. we are using and interacting with sorting algorithms in every day life. in your chapter reading this week, you reviewed many sorting algorithms. find an example of a place in real, everyday life where you interact with, implement or use one of the sorting algorithms covered in chapter 3. for example, while playing cards you may have found yourself implementing the insertion sort algorithm (without knowing it). for this peer interaction, post your example of a place in real, everyday life where you interact with, implement or use one of the sorting algorithms. be sure to provide your us with enough information so that we will thoroughly understand your example and use of a sorting algorithm. once you have made your post, please respond to at least two of your classmates interacting and communicating on the sorting algorithm use in real world context.
Answers
A sorting algorithm is defined as an algorithm that sorts the elements of a list. The most commonly used sequences are numerical sequence and lexicographical sequence, ascending or descending.
A sorting algorithm is used to reorder an array or list of elements according to an element comparison operator. Comparison operators are used to define a new order of elements in that data structure. Consider example, The above list of characters is sorted in ascending order by their value. That is, characters with lower values are placed before characters with higher values. It is important in real life because it supports the development of the scientific concept that things can be owned and organized into distinct groups (e.g. creatures, cars, weather types, etc.). We will now discuss some real-world examples of using sorting algorithms.
1) Your phone's contact list is sorted. This means that your data is organized in this way so you can easily access the contacts you want from your phone. That is, "I ordered."
2) Paper sorting : Imagine a teacher sorting students' work alphabetically by student name. This type of operation is similar to the functionality of sorting algorithms such as bucket sort. Sorting is more efficient process.
3) Traffic lights : Traffic lights are a good example of how algorithms are used in the real world around us. Next time you get stuck in a car at a red light, think about the algorithm that traffic lights run." Most traffic lights don't automatically switch between green, yellow, and red. This algorithm is a well-established turn-by-turn algorithm that directs traffic correctly. It's in order (it may not seem that way when you're sitting at a red light).
To learn more about sorting algorithm, refer:
https://brainly.com/question/14698104
#SPJ4

graph each system. use the graph to find the solution and to determine the name of the system. system: y=2x+1 y=x-2. solution:____ name of the system:_______
Answers
Given:
\(\begin{gathered} y=2x+1\ldots\ldots\ldots(1) \\ y=x-2\ldots\ldots\ldots(2) \end{gathered}\)To find the solutions:
Let us find three points to plot the graph.
From equation (1),
From equation (2),
Then, the graph is,
Hence, the solution is (-3, -5).



A sign in a bakery gives these options:
15 cupcakes for $26
24 cupcakes for $42
40 cupcakes for $66
Find each unit price to the nearest cent, and show your reasoning.
Which option gives the lowest unit price?
Answers
write an equation for the line through the point (-7,-4) and parallel to the line y=8x-4 in point-slope form
Answers
The equation for the line through the point (-7,-4) and parallel to the line y = 8x - 4 in point-slope form is y = 8x + 52
How to determine the equation of the second line?The first equation is given as
y = 8x - 4
The slope of the above equation is
m = 8
Parallel lines have equal slope
So, the slope of the other line is
m = 8
The equation is then calculated as
y = m(x - x1) + y1
Where
m = 8
(x1, y1) = (-7, -4)
So, we have
y = 8(x + 7) - 4
Expand
y = 8x + 56 - 4
Evaluate the difference
y = 8x + 52
Hence, the equation for the line through the point (-7,-4) and parallel to the line y = 8x - 4 in point-slope form is y = 8x + 52
Read more about linear equation at:
brainly.com/question/14323743
#SPJ1
solve the triangle for which angle a =30\degree, angle b=45\degree, and a=20
Answers
The triangle for which angle a =30\degree, angle b=45\degree, and a=20, side a ≈ 20, side b ≈ 28.284, and side c ≈ 38.636
Two angles (a and b) and one side (a) are provided for us to solve the triangle. Let's call the side across from angle a side A, the side across from angle b side B, and the side across from the final angle (angle c) side C.
Here, it is given that,
angle a = 30 degrees
angle b = 45 degrees
side a = 20
angle c = 180 - (angle a + angle b)
angle c = 180 - (30 + 45)
angle c = 180 - 75
angle c = 105 degrees
We know that, a/sin(A) = b/sin(B) = c/sin(C)
a/sin(A) = b/sin(B) = c/sin(C)
20/sin(30) = b/sin(45) = c/sin(105)
b/sin(45) = 20/sin(30)
b = (sin(45) * 20) / sin(30)
b ≈ (0.7071 * 20) / 0.5
b ≈ 14.142 / 0.5
b ≈ 28.284
Now,
c/sin(105) = 20/sin(30)
c = (sin(105) * 20) / sin(30)
c ≈ (0.9659 * 20) / 0.5
c ≈ 19.318 / 0.5
c ≈ 38.636
Thus, side a ≈ 20, side b ≈ 28.284, and side c ≈ 38.636.
For more details regarding triangle, visit:
https://brainly.com/question/2773823
#SPJ1
Here are a few pairs of positive numbers whose sum is 34. (3 pts)
a. Find the product of each pair of numbers.
First
Number
1
4
8
14
Second
Number
33
30
26
20
b. Which pair of numbers that have a sum of 34 will produce the largest possible
product? What is that product?
Answers
Answer: 280
Step-by-step explanation:
The products of each pair of numbers are:
1 x 33 = 33
4 x 30 = 120
8 x 26 = 208
14 x 20 = 280
b. To find the pair of numbers that will produce the largest possible product, we need to look for the pair with the closest product to 340 (the square of 17, which is the average of the two numbers).
The pair of numbers with the closest product to 340 is 14 and 20, whose product is 280. Therefore, the pair of numbers that will produce the largest possible product is 14 and 20, and the product is 280.
PLEASE HELP ASAP WILL GIVE BRAINLEIST!!!
Mrs. Ross is going to invest $500. Her bank offers an interest rate of 4%. How much will be in her account after 4 years?
Answers
Answer:
$ 3125.00
Step-by-step explanation:
P=\(\frac{SI * 100 }{R*T}\)=
\(\frac{500*100 }{4*4}\) = \(\frac{50000}{16}\) = $3125.00
You roll a six-sided die.
Event A: Roll an odd number.
Event B: Roll a number less than 5.
Find P(A or B). Express you answer as a fraction in simplest form.
Answers
P(A or B) =
Formula: P(AUB)=P(A)+P(B)-P(A n B)
We roll six-sided die.
Then sample space ={1,2,3,4,5,6}
And
Event A: Roll an odd number.
Odd numbers are {1,3,5}
Event B: Roll a number less than 5
Number less than 5 are {1,2,3,4}
So, Probability P(A)=
Probability P(B)=
Now, the odd number which is less than 5 are {1,3}
So, P(A n B)=
Since P(AUB)=P(A)+P(B)-P(A n B)
Therefore, P(A or B) = 1/6
Let f(x) = 7x^2 - 7x(a) Use the limit process or derivative to find the slope of the line tangent to the graph of f at x = 4. Slope at x = 4:____(b) Find an equation of the line tangent to the graph of f at x = 4Tangent line: y =
Answers
We are given the following function:
\(f\mleft(x\mright)=7x^2-7x\)Part A. We are asked to determine the slope of the tangent line at "x = 4".
To determine the slope of the tangent line at a point "x = a" we use the following limit definition:
\(m=\lim _{x\rightarrow a}\frac{f(x)-f(a)}{x-a}\)Now, we substitute the value of "x = 4" in the limit definition, we get:
\(m=\lim _{x\rightarrow4}\frac{f(x)-f(4)}{x-4}\)Now, we determine the value of f(4) from the given function;
\(f(4)=7(4)^2-7(4)\)Solving the operations:
\(f(4)=84\)Now, we substitute the values in the limit:
\(m=\lim _{x\rightarrow4}\frac{7x^2-7x-84}{x-4}\)Now, we take 7 as a common factor:
\(m=\lim _{x\rightarrow4}\frac{7(x^2-x-12)}{x-4}\)Now, we factor de denominator, we get:
\(m=\lim _{x\rightarrow4}\frac{7(x+3)(x-4)}{x-4}\)Now, we cancel out the "x - 4":
\(m=\lim _{x\rightarrow4}7(x+3)\)Now, we substitute the values of "x = 4", we get:
\(m=\lim _{x\rightarrow4}7(x+3)=7(4+3)=49\)Therefore, the slope is 49.
Part B. We are asked to determine the equation of the tangent line. We have that the general form of a line equation is:
\(y=mx+b\)From part A we have that the slope is 49, therefore, we have:
\(y=49x+b\)Now, we need to determine a point on the line to determine the value of "b". We already have that the point "x = 4" is part of the line. To determine the corresponding value of "y" we substitute in the given function:
\(f(4)=7(4)^2-7(4)\)Solving we get:
\(f(4)=84\)Therefore, the point (x, y) = (4, 84) is on the line. Substituting we get:
\(84=49(4)+b\)Solving the product:
\(84=196+b\)Now, we subtract 196 from both sides:
\(\begin{gathered} 84-196=b \\ -112=b \end{gathered}\)Now, we substitute the value in the line equation:
\(y=49x-112\)Thus we have determined the equation of the tangent line.
Joe bought a box of laundry detergent that contains 195 scoops. Each load of laundry uses 2 1/2 scoops. How many loads of laundry can Joe do with this one box? The box of detergent cost $19.99. How much is he paying for each load of laundry that he washes? The question we are answering is: How much is he paying for each load of laundry that he washes? Round to the nearest cent. 0.25, 0.26, 0.30
Answers
Answer:
a) Number of laundries he can do with this box = 78 laundries.
b) Price he paying for each load = 0.26 $
Step-by-step explanation:
For f(x) = x + 4√
x
+
4
, what is the value of the function when x = 8? Round to the nearest hundredth.
Answers
f(8) = 8 + 4√(8+4) = 8 + 4√12 ≈ 12.03
Rounding this to the nearest hundredth gives 12.03.
solve the system of two linear inequalities graphically.
y≤−5x−10
y>x+2
Answers
y≤−5x−10 and y>x+2 The shaded region satisfies both inequalities and represents the solution to the system of linear inequalities.
To graphically solve this system of linear inequalities, we can start by graphing each inequality on the same coordinate system:
First, let's graph the inequality y ≤ -5x - 10. We can start by graphing the line y = -5x - 10, which is the boundary line of the inequality. We can plot two points on this line, say (-2,0) and (0,-10), and draw a straight line passing through them.
Next, we need to determine which side of the line satisfies the inequality y ≤ -5x - 10. We can choose any point on one side of the line, say (0,0), and test it in the inequality. If y ≤ -5x - 10 is true for (0,0), then that side of the line satisfies the inequality. Otherwise, the other side satisfies the inequality. Testing (0,0), we have:
0 ≤ -5(0) - 10
0 ≤ -10
This is false, so the side of the line containing the origin does not satisfy the inequality. The other side of the line does.
Now, let's graph the inequality y > x + 2. We can start by graphing the line y = x + 2, which is the boundary line of the inequality. We can plot two points on this line, say (-2,0) and (0,2), and draw a straight line passing through them.
Next, we need to determine which side of the line satisfies the inequality y > x + 2. We can choose any point on one side of the line, say (0,0), and test it in the inequality. If y > x + 2 is true for (0,0), then that side of the line satisfies the inequality. Otherwise, the other side satisfies the inequality. Testing (0,0), we have:
0 > 0 + 2
This is false, so the side of the line containing the origin does not satisfy the inequality. The other side of the line does.
Now, we can shade the region that satisfies both inequalities. The shaded region is the region that is below the line y = -5x - 10 (including the line itself) and above the line y = x + 2 (excluding the line itself).
The shaded region is shown below:
Graph of y≤−5x−10 and y>x+2
The shaded region satisfies both inequalities and represents the solution to the system of linear inequalities.
for such more question on linear inequalities.
https://brainly.com/question/5370236
#SPJ11

f(x)=x^2. What is g(x)?

Answers
Answer:
D, g(x) = 1/4 x^2
Step-by-step explanation:
You can try plugging in the x and y values into each equation. The answer to this would be D, where if you plug in 2 as the x value, you get 1/4 * 4 which equals 1. This also makes sense because 2x would have a narrower curve while 1/2x would have a wider curve.
4
Acellus
Find the lateral area of this cone.
Leave your answer in terms of pie
4ft
3ft
LA = [ ? ] pie ft2
Hint: Lateral Area of a Cone = mre
Where l = slant height
Enter
Answers
Answer:12
Step-by-step explanation: I multiplied 3 times 4
The Lateral Surface Area of cone is 12 π ft³
what is Lateral Surface area of Cone?The lateral area of a cone is defined as the area covered by the curved surface of the cone. It is also called lateral surface area (LSA) or curved surface area (CSA) of a cone. A cone is a 3-D object which tapers smoothly from the flat circular base to a point. In other words, it is a shape formed by a set of line segments coming from the base that connects to a common point
example:
Find the lateral area of a cone having base radius of 21 units and height of 20 units. (Use π = 22/7)
Solution: Given that r = 21 units and h = 20 units
Thus, slant height of the cone, l = √(r2 + h2) = √(212 + 202) = √(441 + 400) = √841 = 29 units
We know, the lateral area of the cone = πrL
Lateral area of a cone = (22/7) × 21 × 29
= 22 × 3 × 29
= 1914 units2
Answer: The lateral surface area of the given cone is 1914 units2
Given:
l= 4 ft
r= 3 ft
Lateral area = πrl
Lateral area = π * 3 * 4
Lateral area = 12 π ft³
Learn more about this concept here:
https://brainly.com/question/23720100
#SPJ2
The answer and how to do it

Answers
Answer:
v ≈ 4 cm
Step-by-step explanation:
using the Sine rule in Δ VWX
\(\frac{v}{sinV}\) = \(\frac{w}{sinW}\)
where v = WX and w = VX
∠ W = 180° - (126 + 21)° = 180° - 147° = 33° , then
\(\frac{v}{sin21}\) = \(\frac{6}{sin33}\) ( cross- multiply )
v × sin33° = 6 × sin21° ( divide both sides by sin33° )
v = \(\frac{6sin21}{sin33}\) ≈ 4 cm ( to the nearest cm )
is it possible to write vector (-5,6) as a linear combination of vectors (1,2) and (3,4)
Answers
Answer:
Step-by-step explanation:
-5i+6j=x(1i+2j)+y(3i+4j)
-5=x+3y(multiply by 2)
6=2x+4y
-10=2x+6y
subtract
16=-2y
y=-8
-5=x+3(-8)
x=-5+24=19
-5i+6j=19(i+2j)-8(3i+4j)
so we can write (-5,6) as a linear combination of (1,2) and (3,4)
A particle moves along line segments from the origin to the points (1, 0, 0), (1, 4, 1), (0, 4, 1), and back to the origin under the influence of the force field below. Find the work done.
F(x,y,z) = z2 i + 3xy j + 4y2 k
Answers
As per the given line segments, the work done by the particle is 78N.
Line segments:
In meth, then bounded by two distinct points on a line is called as line segment.
Given,
Here we have a particle moves along line segments from the origin to the points (1, 0, 0), (1, 4, 1), (0, 4, 1), and back to the origin under the influence of the force field below.
And we need to find the work done.
While we have the function in the given question as,
=> F(x,y,z) = z²i + 3xy j + 4y²k
Here we have consider that, If C is the path the particle follows, then work done is ∫ₓᵃ F dx.
Then according to the question the force F(x,y,z) = z²i + 3xy j + 4y²k and all four points are in the plane is written as,
z = 1/4 y
So, if S is the at surface with boundary C, so that S is the portion of the plane over the rectangle is calculated as,
=> D=[0,2] x [0,4].
Then as per the stroke's theorem,
=> ∫∫[2z(0) + 3z(1/4) + 4y]
=> ∫∫3z/4 + 4y
=> [39]₀²
=> 78
To know more about Line segments here.
https://brainly.com/question/25727583
#SPJ4
Which of the following sets of ordered pairs represents a function?
{(−3, −3), (−2, −2), (−1, −1), (0, 0), (1, 1)}
{(−3, −3), (−3, −2), (−3, −1), (−3, 0), (−4, −1)}
{(−3, −3), (−3, −1), (−1, −2), (−1, −1), (−1, 0)}
{(−3 −3), (−3, 0), (−1, −3), (0, −3), (−1, −1)}
Answers
The 1st one/Top one.
X value is different each time. Function can have the same y-value (3, 1), (2, 1) but can't have the same x-value (3, 1) (3, 3)
what is the value of the expression
(9+15) ÷ 3 + 2? I'm grandma and dont understand. I came up with 4.4
is that right?
Answers
(9+15) = 24
Divide the answer from the top ‘24’ by 3
24 divided by 3 = 8
And then add the answer from that which is ‘8’ to 2
8+2= 10 and you answer is 10
Y+2=1/3(x-8) what is the slope
Answers
The slope of the equation of the line described is equal to 1/3.
What is a slope?A slope is also referred to as gradient and it's typically used to describe both the ratio, direction and steepness of the function of a straight line.
How to calculate the slope of a line?Mathematically, the slope of any straight line can be calculated by using this formula;
\(Slope = \frac{Change\;in\;y\;axis}{Change\;in\;x\;axis}\\\\Slope = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}\)
Mathematically, the standard form of the equation of a straight line is given by;
y = mx + c
Where:
x and y are the points.m is the slope.c is the intercept.y + 2 = 1/3(x-8)
y + 2 = 1/3x - 8/3
y = 1/3x - 8/3 - 2
y = 1/3x - 2/3
Therefore, the slope of the equation of the line described is equal to 1/3.
Read more on slope here: brainly.com/question/3493733
#SPJ1
cot(sin-1) square rootx2
Answers
The algebric expression \(cot(sin^{(-1)}\sqrt{(x^2}\)simplifies to sqrt(1 - |x|^2) / |x|.
The expression "cot(sin^(-1)(sqrt(x^2)))" involves trigonometric and square root functions. Let's break it down step by step to simplify the expression.
Inside the square root: x^2.
The square root of x^2 is |x| (the absolute value of x), as the square root eliminates the square and keeps the positive value.
The expression sin^(-1)(sqrt(x^2)) is equivalent to arcsin(sqrt(x^2)).
Since we already know that the square root of x^2 is |x|, we can rewrite the expression as arcsin(|x|).
Now, we have cot(arcsin(|x|)).
The cotangent (cot) of an angle is equal to the reciprocal of the tangent (tan) of the same angle.
So, cot(arcsin(|x|)) can be written as 1 / tan(arcsin(|x|)).
Using the inverse trigonometric identity, tan(arcsin(x)) = x / sqrt(1 - x^2), we can simplify further.
In our case, x = |x|.
Therefore, tan(arcsin(|x|)) = |x| / sqrt(1 - |x|^2).
Substituting this result back into the expression, we have 1 / (|x| / sqrt(1 - |x|^2)).
To divide by a fraction, we multiply by its reciprocal.
Hence, the final simplification of the expression is sqrt(1 - |x|^2) / |x|.
For more such question on algebric expression visit:
https://brainly.com/question/4344214
#SPJ8
What change do you have to make to the graph of f (x) = 7x in order to graph the function g (x) = 7x+10?
Answers
To graph the function g(x) = 7x + 10, we shift the graph of f(x) = 7x vertically by adding a constant term of +10. This means every y-coordinate on the graph increases by 10 units. The slope of the line remains the same at 7. The resulting graph is a straight line passing through (0, 10) with a slope of 7.
To graph the function g(x) = 7x + 10, you need to make the following change to the graph of f(x) = 7x:
1. Translation: The graph of f(x) = 7x can be shifted vertically by adding a constant term to the equation. In this case, the constant term is +10.
Here's how you can do it step by step:
1. Start with the graph of f(x) = 7x, which is a straight line passing through the origin (0,0) with a slope of 7.
2. To shift the graph vertically, add the constant term +10 to the equation. Now, the equation becomes g(x) = 7x + 10.
3. The constant term of +10 means that every y-coordinate of the points on the graph will increase by 10 units. For example, the point (0,0) on the original graph will shift to (0,10) on the new graph.
4. Similarly, if you take any other point on the original graph, such as (1,7), the corresponding point on the new graph will be (1,17) since you add 10 to the y-coordinate.
5. Keep in mind that the slope of the line remains the same, as only the y-values are affected. So, the new graph will still have a slope of 7.
By making this change, you will have successfully graphed the function g(x) = 7x + 10.
For more such questions graph,Click on
https://brainly.com/question/19040584
#SPJ8
In how many ways can a quality-control engineer select a sample of3 transistors for testing frm a batch of 100 transistors?

Answers
Answer:
161700 ways.
Step-by-step explanation:
The order in which the transistors are chosen is not important. This means that we use the combinations formula to solve this question.
Combinations formula:
\(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
In this question:
3 transistors from a set of 100. So
\(C_{100,3} = \frac{100!}{3!(100-3)!} = 161700\)
So 161700 ways.
2 1/2 ÷ by 5/8=? Whats the answer
Answers
Answer:
4
Step-by-step explanation:
5/8 x 4 =2.5
2.5 is also 2 1/2
Explanation: 2 1
2
÷
5
8
=
5
2
÷
5
8
=
5
2
×
8
5
=
5 × 8
2 × 5
=
40
10
=
40 ÷ 10
10 ÷ 10
= 4
Ryan has 21 pencils. He wants to put the same number of pencils in each of 3 pencil holders. How many pencils will he put in each pencil holder
Answers
21 divided by 3 equals 7
7 pencils in each holder
:]
Ryan will put 7 pencils in each pencil holder.
What is the unitary method?The unitary method is a method for solving a problem by the first value of a single unit and then finding the value by multiplying the single value. If an event can occur in "m" in different ways and if following it, a second event can occur in "n" ways; then the two events in succession can occur in m × n ways.
Given that Ryan has 21 pencils, wants to put the same number of pencils in each of the 3 pencil holders.
Pencil = 21
Pencil holder = 3
Therefore, we will do as 21 divided by 3
21/3 = 7
Hence, there are 7 pencils in each pencil holder.
To learn more about the unitary method, please visit the link below;
https://brainly.com/question/23423168
#SPJ2
Which set of three angles could represent the interior angles of a triangle?

Answers
Answer:
As a claustrophobia, I can ????
O 35°, 35°, 20°
GIVING BRAINLIST PLEASE HELP!!!
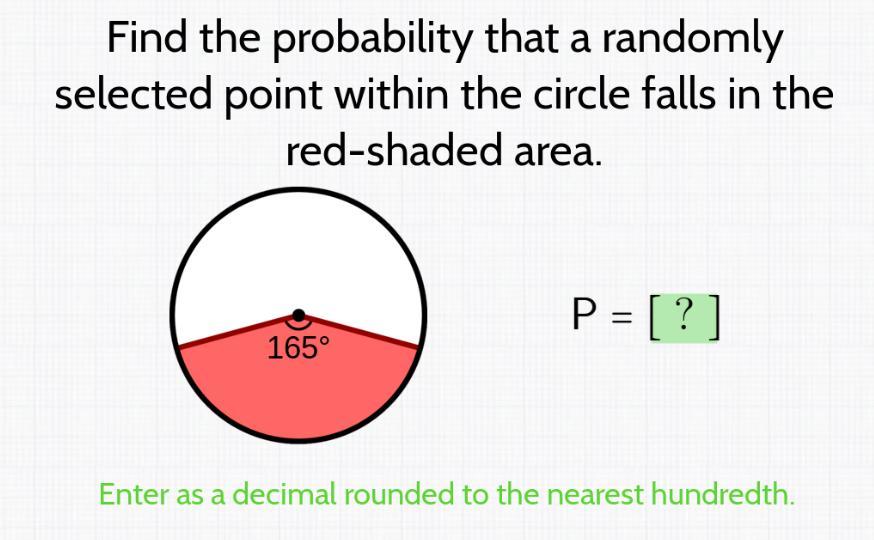
Answers
The probability that a randomly selected point within the circle would fall in the red- shaded area is 45. 833 %
How to find the probability ?The arc that is covered by the red - shaded area in the circle has a degree measure of 165 degrees. This is out of the total circle angle measure of 360 degrees.
This therefore means that the probability that a randomly selected point within the circle would fall in the red- shaded area can be found to be :
= Angle measure of red - shaped area / Total area x 100 %
= 165 / 360 x 100 %
=0. 45833 x 100 %
= 45. 833 %
Find out more on probability at https://brainly.com/question/22690728
#SPJ1
.
3. The speed of light can be written as any of the three below:
286,000 miles per second,
503,360,000 yards per second,
or 1,510,080 feet per second.
a.
Use the speeds of light from above to answer the following question. Which of the
noft
following correctly records the speed of light using scientific notation?
2.86 x 10milespersecond
b. 5033.6 x 108 yardsper second
C.
1.51008x10-feetpersecond
d. none of the above

Answers
Answer:
D
Step-by-step explanation: