Let f(x)=-2x+7 and g(x)=-6x+3. Find f•g and state it’s domain
Answers
Answer:
f(g(x)) = 12x + 1;The domain is all real numbers---------------------
Given functions f(x)=-2x+7 and g(x)=-6x+3.
Find the composite function f·g:
f(g(x)) = - 2(-6x + 3) + 7 = 12x - 6 + 7 = 12x + 1This is a linear function so the domain is all real numbers.
The domain of f•g is the set of all real numbers since there are no restrictions or conditions given for x. Therefore, the domain of f•g is (-∞, +∞) or (-∞, ∞).
What is domain?
The domain of a function is the set of values that we are allowed to plug into our function. This set is the x values in a function such as f(x). The range of a function is the set of values that the function assumes. This set is the values that the function shoots out after we plug an x value in.
To find f•g (the dot product of f and g), we multiply the corresponding components of the two vectors and then sum the products.
f(x) = -2x + 7
g(x) = -6x + 3
To find f•g, we multiply the corresponding coefficients:
\(f•g = (-2x)(-6x) + (7)(3)\)
\(= 12x^2 + 21\)
The domain of f•g is the set of all real numbers since there are no restrictions or conditions given for x. Therefore, the domain of f•g is (-∞, +∞) or (-∞, ∞).
To know more about domain visit:
https://brainly.com/question/26098895
#SPJ4
Related Questions
mark any solutions to the equation 2cos^2x-1=0
Answers
The solutions to the equation 2cos^2x-1=0 is x = π/4, -π/4 (in radians), x = 45 degrees, -45 degrees (in degrees).
To solve the equation 2cos^2(x) - 1 = 0, we can follow these steps:
Step 1: Add 1 to both sides of the equation to isolate the cosine term:
2cos^2(x) = 1
Step 2: Divide both sides of the equation by 2 to solve for cos^2(x):
cos^2(x) = 1/2
Step 3: Take the square root of both sides of the equation:
cos(x) = ±√(1/2)
Step 4: Find the solutions for x by taking the inverse cosine (cos⁻¹) of both sides:
x = cos⁻¹(±√(1/2))
Now, let's evaluate the inverse cosine of ±√(1/2) to find the solutions for x:
For cos⁻¹(√(1/2)):
x = cos⁻¹(√(1/2))
x = π/4 or 45 degrees
For cos⁻¹(-√(1/2)):
x = cos⁻¹(-√(1/2))
x = -π/4 or -45 degrees
Therefore, the solutions to the equation 2cos^2(x) - 1 = 0 are:
x = π/4, -π/4 (in radians)
x = 45 degrees, -45 degrees (in degrees)
Know more about equation here:
https://brainly.com/question/17145398
#SPJ11
Which shows Angle P O Q?
Answers
Answer: Which shows Angle P O Q? Option (A)
(A) Q Line segments Q O and O P combine to form an angle.
P
R
P
Step-by-step explanation:
Answer:
its a
Step-by-step explanation:
Please helppppp meeeeeeee

Answers
Answer:
I Also need the answer plese helep ussss
Step-by-step explanation:
The temperature is -3°F at 7 A.M. During the next three hours, the temperature increases 13°F. What is the temperature at 10 AM?
A -16°F
B-16°F
C- 10°F
D-10°F
Answers
What is −20÷4/5?please help me
−25
−16
−1/16
−1/25
Answers
Answer:
-25
Step-by-step explanation:
Quadrilateral MATH is congruent to quadrilateral WXYZ. Which
statement is always true?
(1) MA - XY
(2) m/H=mZW
(3) Quadrilateral WXYZ can be mapped onto quadrilateral MATH using a
sequence of rigid motions.
(4) Quadrilateral MATH and quadrilateral WXYZ are the same shape, but
not necessarily the same size.

Answers
Answer:
2
Step-by-step explanation:
The true statement is Quadrilateral WXYZ can be mapped onto quadrilateral MATH using a sequence of rigid motions.
What is Congruency?The triangles are said to be congruent when two angles and a non-included side of one triangle match the corresponding angles and sides of another triangle.
Given:
MATH is congruent to quadrilateral WXYZ.
Then congruent sides are
MA= WX
AT = XY
TH = YZ
and, congruent angles are
<M = <W
<A = <X
<T= <Y
<H = <Z
So, if the quadrilateral is congruent then they equal in measure.
Hence, the true statement is Quadrilateral WXYZ can be mapped onto quadrilateral MATH using a sequence of rigid motions.
Learn more about Congruent here:
https://brainly.com/question/12413243
#SPJ2
HELP ME PLZ !!!!!!!!!!!!!!!!!!

Answers
Construct a truth table for each of these compound propositions
a) p → ⇁p
b) p ↔ ⇁p
c) p ⊕ (p V q) d) (p ∧ q) → (p V q) e) (p → ⇁p) ↔ (p ↔ q) f) (p ↔ q) ⊕ (p ↔ ⇁q)
Answers
After considering the given data we conclude that there truth table is possible and is placed in the given figures concerning every sub question.
A truth table is a overview that projects the truth-value of one or more compound propositions for each possible combination of truth-values of the propositions starting up the compound ones.
Every row of the table represents a possible combination of truth-values for the component propositions of the compound, and the count of rows is described by the range of possible combinations.
For instance, if the compound has just two component propositions, it comprises four possibilities and then four rows to the table. The truth-value of the compound is projected on each row comprising the truth functional operator.
To learn more about truth table
https://brainly.com/question/28605215
#SPJ4



Columbus and Dayton are 9.7 cm apart from each other on a map that has a scale of 1.1 cm: 15 mi. How far apart are the two cities? Round your answer to the nearest tenth.
A. 151.6 miles
B. 155.4 miles
C. 122.4 miles
D. 132.3 miles
Answers
Answer:
D. 132.3 miles
Step-by-step explanation:
Create a proportion where x is the actual distance between the two cities.
\(\frac{1.1}{15}\) = \(\frac{9.7}{x}\)
Cross multiply and solve for x:
1.1x = 145.5
x = 132.3
So, the two cities are 132.3 miles apart.
The correct answer is D. 132.3 miles
Find f(x) if f(2) = 1 and the tangent line at x has slope (x − 1)ex2 − 2x.
f(x)= _____________
Answers
If f(2) = 1 and the tangent line at x has slope (x − 1)ex2 − 2x. f(x) = ((x^2 - 2x + 1)/2)e^(x^2 - 2x).
To find f(x), we'll first integrate the given slope function to obtain the original function. The slope of the tangent line is given as (x - 1)e^(x^2 - 2x).
Let F'(x) = (x - 1)e^(x^2 - 2x). To find f(x), we need to integrate F'(x) with respect to x:
∫(x - 1)e^(x^2 - 2x) dx
Now, we can use substitution. Let u = x^2 - 2x, then du = (2x - 2) dx. Therefore, the integral becomes:
∫((u + 1)/2)e^u du
Now, we can integrate by parts. Let v = e^u, then dv = e^u du. Let w = (u + 1)/2, then dw = 1/2 du. Using integration by parts formula:
∫w dv = wv - ∫v dw
∫(u + 1)/2 * e^u du = ((u + 1)/2)e^u - ∫(1/2)e^u du
Now integrate the remaining part:
∫(1/2)e^u du = (1/2)e^u + C
Substituting back:
f(x) = ((x^2 - 2x + 1)/2)e^(x^2 - 2x) + C
Now, use the given condition f(2) = 1:
1 = ((2^2 - 2*2 + 1)/2)e^(2^2 - 2*2) + C
1 = (1)e^0 + C
C = 0
Know more about integration here;
https://brainly.com/question/18125359
#SPJ11
Nicholas bought 24feet of fabric at afabric store. The fabric cost $1.35 per foot, including sales tax. If Nicholaspaid with a $50bill, how much change should he have received?
Answers
Answer:
24x1.35=32.4
He should have recieved $32.40 in change.
An equilateral triangle with side lengths of 8. 7 centimeters is shown. An apothem has a length of a and the radius has a length of 5 centimeters. The apothem and radius form a triangle with a base length of b. Which statements about finding the area of the equilateral triangle are true? Select three options. The apothem can be found using the Pythagorean theorem. The apothem can be found using the tangent ratio. The perimeter of the equilateral triangle is 15 cm. The length of the apothem is approximately 2. 5 cm. The area of the equilateral triangle is approximately 65 cm2.
Answers
The image of the triangle is missing, so i have attached it.
Also, the options are;
A) The apothem can be found using the Pythagorean theorem.
B) The apothem can be found using the tangent ratio.
C) The perimeter of the equilateral triangle is 15 cm.
D) The length of the apothem is approximately 2.5 cm.
E) The area of the equilateral triangle is approximately 65 cm².
Answer:
Options A, B & D are true
Step-by-step explanation:
A) We are told that the triangle is an equilateral triangle.
Thus, the 3 sides equal 8.7 cm.
Now from the image, b is half of one of the sides.
Thus, b = 8.7/2 = 4.35 cm
Now, we want to find the apothem "a".
Using Pythagoras theorem, we have;
a² + 4.35² = 5²
a² = 25 - 18.9225
a² = 6.0775
a = √6.0775
a ≈ 2.5 cm.
Thus, option A is true as Pythagoras theorem was able to calculate the apothem "a"
B) since the main triangle is equilateral, it means each angle is 60°.
Now, the radius line from one corner point to the center will divide the 60° angle into 2 equal parts.
Thus, the angle made by the radius line with the base of the triangle is 60/2 = 30°
Now, from tangent ratios, we know that;
Opposite/Adjacent = tan θ
In the small triangle, opposite is apothem "a" while adjacent is b = 4.35 cm
Thus;
a/4.35 = tan 30
a = 4.35 tan 30
a ≈ 2.5 cm.
Thus, option B is correct as Tangent ratio can be used to find the apothem
C) The perimeter of equilateral triangle = 3x
Where x is length of one side.
One side is 8.7 cm
Thus, perimeter = 3 × 8.7 = 26.1 cm
Thus option C is not correct.
D) From calculations above, we saw that in both options A & B, the apothem is approximately 2.5 cm.
Thus, option D is true.
E) Area of triangle is;
A = ½ × base × height
Base = 8.7 cm
To get height, we will use trigonometric ratio. Thus;
h/8.7 = sin 60°
h = 8.7 sin 60°
Thus;
A = ½ × 8.7 × 8.7 sin 60°
A = 32.77 cm²
Thus is not equal to 65 cm². Thus, option E is not correct.

The statements that are true for the considered equilateral triangle are:
Option A: The apothem can be found using the Pythagorean theorem.Option B: The apothem can be found using the tangent ratio.Option D: The length of the apothem is approximately 2. 5 cm.What is apothem?
For a regular polygon, the apothem is the line segment from the center of the polygon to the mid of one of the sides of the considered polygon.
For this case, referring to the figure attached below, we have:
Length of the apothem = x (assume)The triangle ABC is equilateralLength of line segment from vertex to center (radius) = 5 cmLength of each side of the triangle = 8.7 cmSince the triangle is equilateral, there can be 6 congruent triangles like BOD.
Thus, Area of triangle ABC = 6 × Area of triangle BOD
Area of BOD = \(\dfrac{1}{2} \times x \times 4.35 = 2.175x \: \rm cm^2\)
Area of ABC = \(6 \times 2.175x = 13.05x \: \rm cm^2\)
The length of the apothem is x cm, and can be obtained by using Pythagoras theorem.
We can also use the tangent ratio as the line segment BO is bisecting the internal angle B (each internal angle is of 60 degrees in an equilateral triangle), so angle OBD is of 60/2 = 30 degrees. So using angle and the fact that tangent ratio is ratio of side opposite to angle and the remaining adjacent side(not hypotenuse).
\(tan(30^\circ) = x/4.35 \implies x = 4.35 \times \tan(30^\circ) \approx 2.5 \: \rm cm\)
Using Pythagoras theorem too, we can get the value of x as:
\(5^2 = 4.35^2 + x^2\\x = \sqrt{25 - 18.9225} \approx 2.465 \: \rm cm \approx 2.5 cm\)
Thus, area of the equilateral triangle ≈ \(13.05 \times x \approx 13.05 \times 2.5 = 32.575 \: \rm cm^2\)
This isn't 65 sq. cm.
Thus, the statements that are true for the considered equilateral triangle are:
Option A: The apothem can be found using the Pythagorean theorem.Option B: The apothem can be found using the tangent ratio.Option D: The length of the apothem is approximately 2. 5 cm.Learn more about tangent ratio here:
https://brainly.com/question/14169279

The elevation of Death Valley, CA is 282 feet below sea level, while the elevation of Riverside, CA is 827 feet above sea level. How much higher is the elevation of Riverside than Death Valley?
Answers
Answer:
Step-by-step explanation:
Death Valley is 282 ft below sea level, so it can be seen as -282
Riverside is 827 ft above sea level, so it is 827
827-(-282)
827+282 = 1109ft
Someone please help explain how to do it and please help me

Answers
Answer: 7
Step-by-step explanation:
First, do 221 divided by 13 to get how many dollars per hour which is 17 and then do 119 divided by 17 to get the amount of hours.
Part 5 of 5
Use your result from the previous step to complete the following statements.
The maximum value of the product, occurring at the vertex of the graph of P(x), is 108. The maximum occurs when x=18.
*********
Therefore...what are the two numbers?
X (smaller value)
(larger value)
Enter an exact number.
Submit Skip (you cannot come back)
Answers
We are given two numbers and we want to find the smaller one, we can use a comparison operator to determine which number is larger and which is smaller. the two numbers are 7 and 18 .
What is the maximum value of the product?Let's say the two numbers are x and y, where x is greater than y.
According to the statement, we have:
x+y = (x-y) + 2y
Simplifying this equation, we get:
x+y = x-y
This is true, since we started with x and y as the two numbers.
So, the statement is always true for any two numbers x and y, where x is greater than y.
Since the maximum value of the product occurs at x=18, which represents the larger number, the smaller number can be found by subtracting it from the sum of the two numbers:
Smaller value = Sum - Larger value
Smaller value = 25 -18
Smaller value = 7
Therefore, the two numbers are 7 and 18 .
Learn more about value here
brainly.com/question/14098515
#SPJ1
Please help!
I really need it asap

Answers
Systematic random sampling has become a popular method of drawing samples in research practices because _____.
Answers
it is a relatively easy way to draw a sample while ensuring randomness is the answer.
Systematic sampling is a probabilistic sampling method in which a researcher selects members of a population at regular intervals. For example, select every 15 people from the list of populations. If the population is in random order, this can mimic the benefits of a simple random sample.
These are generally preferred by researchers because they are easy to implement and understand. The important assumption that the results represent the majority of the normal population ensures that the entire population is sampled equally. The process also provides a higher level of control for systematic sampling compared to other sampling methods. systematic sampling also has a lower risk factor because the data is unlikely to be contaminated.
Learn more about systematic random sampling here:https://brainly.com/question/21100042
#SPJ4
Find extreme point(s) at the interval (-[infinity],[infinity]) and decide if the extreme points are min or max.
a) f(x)=x2 +x–6
b) f(x)=x3 +x2
Use Graphical method to solve the following problems
Draw a graph
Identity the feasible area
Find all corner point feasible solutions (CPFS) and identify the optimal solution if they have any
a) Max s.t.
x1 + x2
2x1 + 5x2 <= 5
x1+ x2<=5
3x1+ x2<=15
x1, x2 >= 0
b) Min s.t.
x1 + x2
-x1+ x2<=5
x2 <= 3
3x1+ x2>=7
x1, x2 >= 0
Answers
a) To find the extreme points and determine if they are minimum or maximum, we need to take the derivative of the function and set it equal to zero.
a) f(x) = x^2 + x - 6
Taking the derivative:
f'(x) = 2x + 1
Setting it equal to zero and solving for x:
2x + 1 = 0
2x = -1
x = -1/2
To determine if it is a minimum or maximum, we can examine the concavity of the function. Since the coefficient of x^2 is positive (1), the function opens upward and the critical point at x = -1/2 is a minimum.
b) f(x) = x^3 + x^2
Taking the derivative:
f'(x) = 3x^2 + 2x
Setting it equal to zero and solving for x:
3x^2 + 2x = 0
x(3x + 2) = 0
This gives two critical points:
x = 0 and x = -2/3
To determine if they are minimum or maximum, we need to examine the concavity of the function. Since the coefficient of x^3 is positive (1), the function opens upward. The critical point at x = 0 is a minimum, while the critical point at x = -2/3 is a maximum.
b) Graphical method:
To solve the problem graphically, we will draw a graph representing the constraints and find the feasible area. Then we will identify the corner point feasible solutions (CPFS) and determine if there is an optimal solution.
a) Maximize subject to:
x1 + x2
2x1 + 5x2 <= 5
x1 + x2 <= 5
3x1 + x2 <= 15
x1, x2 >= 0
b) Minimize subject to:
x1 + x2
-x1 + x2 <= 5
x2 <= 3
3x1 + x2 >= 7
x1, x2 >= 0
Unfortunately, the given optimization problems are incomplete as there are no objective functions specified. Without an objective function, it is not possible to determine an optimal solution or solve the problem graphically.
Please provide the objective function for the optimization problems so that we can proceed with the graphical solution and find the optimal solution, if any.
Learn more about graphical optimization methods and solving linear programming problems.
#SPJ11
a) The extreme point for the function f(x) = x² + x - 6 is a minimum point.
b) The extreme point for the function f(x) = x³ + x² is neither a minimum nor a maximum point.
Step 1: For the function f(x) = x² + x - 6, to find the extreme points, we can take the derivative of the function and set it equal to zero. By solving for x, we can identify the x-coordinate of the extreme point. Taking the second derivative can help determine if it is a minimum or maximum point. In this case, the extreme point is a minimum because the second derivative is positive.
Step 2: For the function f(x) = x³ + x², finding the extreme points follows the same process. However, after taking the derivative and solving for x, we find that there are no critical points. Without any critical points, there are no extreme points, meaning there are no minimum or maximum points for this function.
In summary, for the function f(x) = x² + x - 6, the extreme point is a minimum, while for the function f(x) = x³ + x², there are no extreme points.
Learn more about Function
brainly.com/question/31062578
#SPJ11
HELP HURRY PLS
What is the equation of this line?
y =2/3x
y=3/2x
y= -2/3x
y= -3/2x

Answers
Answer:
y = 2/3x
Step-by-step explanation:
What % of 61,122 is 18,380?
Answers
Answer:
30.07%
Step-by-step explanation:
I'm built different
if l //m and m<4=5x-42 and m<5=-x+82, what is the m<5
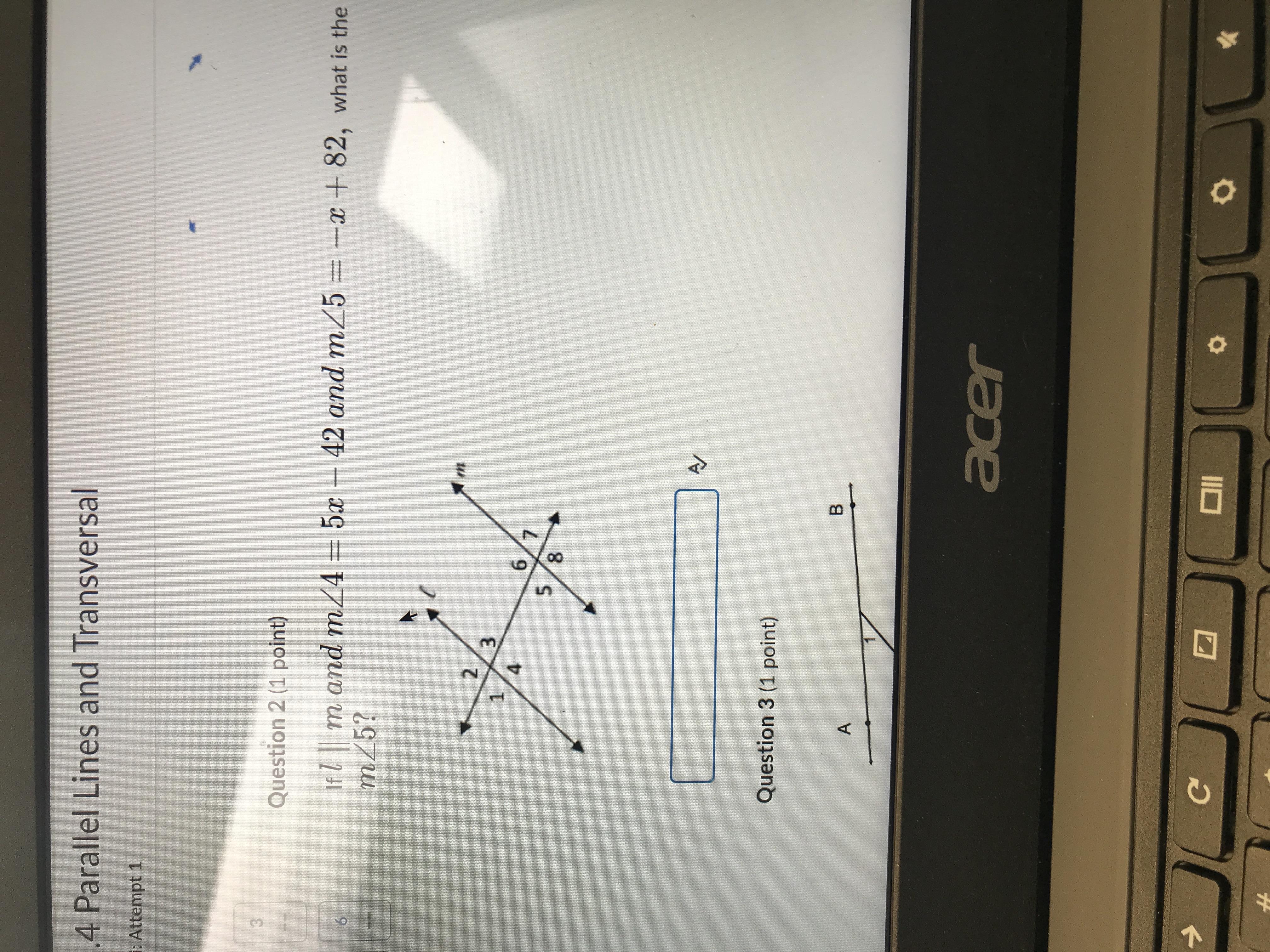
Answers
The measure of <5 is 47
what is parallel lines?Parallel lines are any two or more lines that all lie in the same plane and never cross one another. They are equally spaced apart and have the same incline.
The fundamental characteristics listed below make it simple to recognise parallel lines.
Straight lines that are always the same distance away from one another are called parallel lines.No matter how far apart they are from one another, parallel lines can never intersect.Given:
m<4=5x-42
and m<5=-x+82
as, <4 and <5 are in co- interior angle
<4 + <5 = 180
5x - 42 + (-x + 82) = 180
5x -42 - x + 82= 180
4x +40 = 180
4x = 140
x= 140/4
x= 35
Hence, the measure of <5 = -x+ 82 = -35 + 82 = 47
Learn more about parallel line here:
https://brainly.com/question/16701300
#SPJ1
Question on a picture

Answers
Answer:
c = 0
Step-by-step explanation:
Step 1: Write equation
15 - 5(4c - 7) = 50
Step 2: Solve for c
Distribute -5: 15 - 20c + 35 = 50Combine like terms: -20c + 50 = 50Subtract 50 on both sides: -20c = 0Divide both sides by -20: c = 0Step 3: Check
Plug in c to verify it's a solution.
15 - 5(4(0) - 7) = 50
15 - 5(-7) = 50
15 + 35 = 50
50 = 50
15 - 20c + 35 = 50
50 - 20c = 50
-20c = 0
x = 0
Suppose a survey of 580 women in the United States found that more than 64% are the primary investor in their household. Which part of the survey represents the descriptive branch of statistics? Make an inference based on the results of the survey.64% of women in the sample are the primary investor in their household.
There is an association between U.S. women and being the primary investor in their household.
Answers
The sentence "64% of women in the sample are the principal investor in their household" serves as an example of descriptive statistics.
What will the inference be?This sentence provides a summary of the survey's data and a descriptive statistic (percentage) that characterizes the sample's characteristics.
According to the survey's findings, "there is a correlation between American women and being the principal investor in their household." The sample data are used to draw this conclusion about the population. Despite the fact that the sample is not representative of all American women, the findings indicate that a sizable number of the women in the sample are the principal investors in their households.
Learn more about Surveys here:
brainly.com/question/13532910
#SPJ4
The slope of ( 3, 5 ) with ( 4, 6 )
Answers

If -8-8y=6-2y, what is the value of y?
Answers
Answer:
-7/3
Step-by-step explanation:
The first step is to combine like numbers. Although there are several different ways to go about doing this, I started by adding 2y to both sides which left me with -8-6y=6. I then added 8 to both sides and got 6y=14. Now divide 6 on both sides to get "y" by itself which left me with y = -14/6. When you simplify the answer you get -7/3.
Please help 20 points I’ve been struggling :(
5x + 4y = -16
Complete the steps to convert the equation in standard form to Slope intercept form

Answers
Answer: I'm pretty bad at math, but I made it more simple for you :)
Step-by-step explanation:
The answer is y = 4 + 5x/4
I hope it helped a bit sorryy
What is the squad root of 4 times the square root of 8
Answers
Answer:
1024
Step-by-step explanation:
4x4= 16
8x8= 64
sqrt4 x sqrt8
The square root of 4 is 2.
The square root of 8 is 2.83.
2x2.83=5.66
hope it helps!
5 units to the right of -6 is
Answers
Answer:
-1
Step-by-step explanation:
To solve the problem, it is suggested to use a number line.
~Please look at image attached
We know the following:
If the change is going to the right of the initial point, the change is a positive integer, and the initial point will be added by the change.If the change is going to the left of the initial point, the change is a negative integer and the initial point will be subtracted by the change.Statement: 5 units to the right of -6.
Therefore, we know the following:
Initial starting point: -6Change: +5Ending point: -6 + 5 = -1
Learn more about this topic: https://brainly.com/question/13189025
Number line:
Graph a line with a slope of 1/4 that contains the point (6,3) khan academy

Answers
4y = x + 6 is the equation of the line using the slope value.
What is a line's slope?The steepness of a line segment is explained by the slope of the line. It is a ratio of the vertical x-axis coordinates and the y-axis coordinates. The classification of whether two lines are parallel or perpendicular depends on the slope value.
The parameters for the line segment are as follows, in accordance with the question:
The coordinate points (6, 3) and the slope of a line (1/4) are as follows: (x = 6; y = 3)
Using the line segment's standard equation now: y = mx + c
If (x, y) are coordinates, "m" is the slope, "c" is the y-intercept,
The following results are obtained by replacing the slope and y-intercept values in the formula:
y = mx + c
⇒ 3 = (1/4)(6) + c
⇒ c = 3 - 3/2 = 3/2
Consequently, c = (3/2) is the y-value. intercept's
by changing the slope value and y-intercept value in the line's equation:
y = (1/4)x + (3/2) = 4y = x +6
Consequently, 4y = x + 6 is the equation of the line using the slope value.
To learn more about the slope of a line from the given link:
https://brainly.com/question/16949303
#SPJ10
12. A hot air balloon is flying at an altitude of 1,000 ft. The pilot wants to increase the altitude of
the balloon at 5° angle over the next 500 ft. What will be the balloon's change in altitude?
(sin 5° -0.0872; cos 5º = 0.9962; tan 5° = 0.0875)
A. 25.8 ft
B 43.7 ft
C. 231.4 ft
D. 498 ft
Answers
Balloon's altitude = 43.7ft as
change in altitude/500 = tan 5°
change in altitude = .0875*500
=43.7ft