Let C be the line segment from the point (-4,8) to the point (2,-4), C, be the arc on the parabola y = r2-8 from the point (-4,8) to the point (2, -4), and R be the region enclosed by C and C2. Consid
Answers
Firstly, a line segment is a straight path that connects two points. In this case, the line segment C connects the points (-4,8) and (2,-4).
A point, on the other hand, is a specific location in space that is defined by its coordinates. The points (-4,8) and (2,-4) are two specific points that are being connected by the line segment C.
Now, moving on to the explanation of the problem - we have a line segment C and an arc on a parabola y = r2-8 that connect the same two points (-4,8) and (2,-4). The region R is enclosed by both the line segment C and the arc.
To solve this problem, we need to find the equation of the parabola y = r2-8, which is a basic upward-facing parabola with its vertex at (0,-8). Then, we need to find the points where the parabola intersects with the line segment C, which will give us the two endpoints of the arc C2. Once we have those points, we can calculate the area enclosed by the two curves using integration.
To know more about line segment visit:
https://brainly.in/question/748741
#SPJ11
Related Questions
How do you dilate a triangle by 2?
Answers
Step-by-step explanation:
To dilate the figure by a factor of 2, I will multiply the x and y-value of each point by 2. I plotted all the new points to find the new triangle. To dilate the figure by a factor of 2, I will multiply the x-value of each point by 2.
potatoes cost $0.85 per pound. luke bought 2.75 pounds of potatoes. how much did he pay for the potatoes? round to the nearest cent
Answers
Answer:
Luke pays $2.34
Step-by-step explanation:
2.75 times .85 equals 2.337 which rounded is 2.34
What is the definition of "constant of proportionality"? Define or show an expression to prove your answer
Answers
Answer:
The constant of proportionality is the ratio between two directly proportional quantities. Two quantities are directly proportional when they increase and decrease at the same rate.
(G o o g l e)
Step-by-step explanation:
I hope this helps!
the height of a golf ball after it is hit can be modeled by the equation where represents the number of seconds after the ball is hit, and represents the golf ball height, in feet. a) what is the height of the golf ball at the instant it is hit? feet b) what is the height of the golf ball 2.8 seconds after it is hit? feet c) how long does it take the ball to hit the ground after it is hit? (round answer to three decimal places.) seconds submit question question 3
Answers
a. The height of the golf ball at the instant it is hit is 0 feet.
b. The height of the golf ball 2.8 seconds after it is hit is approximately 62.72 feet.
c. It takes 4 seconds for the golf ball to hit the ground after it is hit.
a) To find the height of the golf ball at the instant it is hit, we need to evaluate the function h when t = 0.
Substituting t = 0 into the given equation, we get:
h = -16(0)² + 64(0) = 0
Therefore, the height of the golf ball at the instant it is hit is 0 feet.
b) To find the height of the golf ball 2.8 seconds after it is hit, we need to evaluate the function h when t = 2.8.
Substituting t = 2.8 into the given equation, we get:
h = -16(2.8)² + 64(2.8) ≈ 62.72
Therefore, the height of the golf ball 2.8 seconds after it is hit is approximately 62.72 feet.
c) To find how long it takes the ball to hit the ground after it is hit, we need to find the value of t when the height is 0.
Setting h = 0 in the given equation, we get:
0 = -16t² + 64t
0 = t(-16t + 64)
t = 0 or t = 4
Since the golf ball was hit upwards, we are only interested in the positive value of t, which is t = 4.
Therefore, it takes 4 seconds for the golf ball to hit the ground after it is hit.
Learn more about the height of the golf ball at
https://brainly.com/question/12456532
#SPJ4
The question is -
The height in feet of a golf ball hit into the air is given by h = − 16t² + 64t, where t is the number of seconds elapsed since the ball was hit, and represents the golf ball height, in feet.
a) what is the height of the golf ball at the instant it is hit?
b) what is the height of the golf ball 2.8 seconds after it is hit?
c) how long does it take the ball to hit the ground after it is hit?
Original price of a computer game: $24.50
Discount: 20%
What is the selling price
Answers
Answer:
You will pay $19.6 for a item with original price of $24.50 when discounted 20%. In this example, if you buy an item at $24.50 with 20% discount, you will pay 24.50 - 4.9 = 19.6 dollars.
Step-by-step explanation:
10. A museum gift shop sells hats with embroidered logos of the museum.
The hats are available in small, medium, and large sizes. They are available
in the colors red and green.
Make a tree diagram or a table to represent all possible varieties of hats sold at
the museum.
Answers

Calculate the volume of liquid that would fill the bowl of the glass. Show all your work.

Answers
Answer:
52.36
Step-by-step explanation:
Formula to find volume in a cone is
V = pi • radius^2 h/3
So we fill in the numbers
V = pi •
the radius is half of diameter,
The diameter is 5
So it's
V = pi • 2.5
since it's half of 5
V = pi • 2.5^2 h/3
the height is 8 so we fill it in
V = pi • 2.5^2 8/3
When calculated, you get..
52.36
The volume of the liquid which can fill the bowl of the glass (in shape of cone) with the liquid is 49.74 cm³.
What is of volume of solid?Volume of solid is the amount of quantity, which is obtained by the solid or object in the 3 dimensional space.
The volume of the cone can be given as,
\(V=\dfrac{1}{3}\pi r^2\sqrt{l^2-r^2}\)
Here, (r) is the radius of the base of the cone and (l) is the slant height of the cone.
Here, the diameter of the cone is 5 cm. thus the radius of the cone is,
\(r=\dfrac{5}{2}\\r=2.5\rm cm\)
The slant height of the cone is 8 cm. Thus, put the value to find the volume of cone as,
\(V=\dfrac{1}{3}\pi (2.5)^2\sqrt{(8)^2-(2.5)^2}\\V\cong 49.74\rm cm^3\)
Thus the volume of the liquid which can fill the bowl of the glass (in shape of cone) with the liquid is 49.74 cm³.
Learn more about the volume of solid here;
https://brainly.com/question/1355179
Calculate the distance between the points M=(-1, -2) and C=(-9, 2) in the coordinate plane.
Round your answer to the nearest hundredth.
Answers
Answer:
nearest hundredth 8.944
Step-by-step explanation:
d = √((x2-x1)2 + (y2-y1)2)
Step by step procedure:
Find the difference between coordinates:
(x2-x1) = (-9 - -1) = -8
(y2-y1) = (2 - -2) = 4
Square the results and sum them up:
(-8)2 + (4)2 = 64 + 16 = 80
Now Find the square root and that's your result:
Exact solution: √80 = 4√5
Approximate solution: 8.944
Convert the credit card rate to the APR. Ohio, 0.02192% daily rate. Please round your answer to the nearest percent. (zero decimal place.) Enter only the number without $ sign.
Answers
Answer:
8%
Step-by-step explanation:
APR means annual percentage rate.
To convert the daily rate to an APR, multiply the daily rate by the number of days in a year
365 days = 1 year
0.02192% x 365 = 8.0008%
To round off to the nearest percent, look at the first number after the decimal, if it is less than 5, add zero to the units term, If it is equal or greater than 5, add 1 to the units term.
The tenth digit is 0, so the number would be rounded off to 8%
plz telll me i chose c right or o?

Answers
Answer:
Yes, C is the answer
Step-by-step explanation:
Answer:
I think c is the answer
I solved the equation 40/100×127
The General Social Survey asked 1676 people how many hours per day they were able to relax. The results are presented in the following table: 0 114 1 156 2 336 3 251 4 316 5 231 6 149
7 33
8 60
Total 1676 Consider these 1676 people to be a population. Let X be the number of hours of relaxation for person sampled at random from this population a) Construct the probability distribution of X. (3 marks) b) Find the probability that a person relaxes more than 4 hours per day. (2 marks) c) Find the probability that a person relaxes from 2 to 6 hours per day d) Find the probability that a person does not relax at all (2 marks) e) Compute the mean Mx. (3 marks) f) Compute the standard deviation Ox: (3 marks)
Answers
The probability distribution of the number of hours per day people are able to relax is constructed, and probabilities of relaxing more than 4 hours, between 2 to 6 hours, and not relaxing at all are 0.283, 0.767 and 0.068 respectively. The mean and standard deviation are 3.326 hours and 1.950 hours (approx.) respectively.
The probability distribution of X is:
X Frequency Probability
0 114 0.068
1 156 0.093
2 336 0.201
3 251 0.150
4 316 0.189
5 231 0.138
6 149 0.089
7 33 0.020
8 60 0.036
1676 1.000
The probability that a person relaxes more than 4 hours per day is:
P(X > 4) = P(X = 5) + P(X = 6) + P(X = 7) + P(X = 8)
= 0.138 + 0.089 + 0.020 + 0.036
= 0.283
The probability that a person relaxes from 2 to 6 hours per day is:
P(2 ≤ X ≤ 6) = P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6)
= 0.201 + 0.150 + 0.189 + 0.138 + 0.089
= 0.767
The probability that a person does not relax at all is:
P(X = 0) = 0.068
The mean Mx is:
Mx = Σ(X * P(X))
= 00.068 + 10.093 + 20.201 + 30.150 + 40.189 + 50.138 + 60.089 + 70.020 + 8*0.036
= 3.326 hours
The standard deviation Ox is:
Ox = sqrt[Σ(X^2 * P(X)) - Mx^2]
= sqrt[(0^20.068)+(1^20.093)+(2^20.201)+(3^20.150)+(4^20.189)+(5^20.138)+(6^20.089)+(7^20.020)+(8^2*0.036) - 3.326^2]
= 1.950 hours (approx.)
To know more about standard deviation:
https://brainly.com/question/23907081
#SPJ4
Consider the trinomial x2 – 9x + 18. Which pair of numbers has a product of ac and a sum of b? What is the factored form of the trinomial?
Answers
Answer:
(x-6)*(x-3)
Step-by-step explanation:
a*c
1*18=18
Factors of 18 are:
1, 2, 3, 6, 9, 18
The equation has +18 meaning both signs must be the same; - - or + +
The only two factors that work are -3 and -6
The factored form will be (x-6)*(x-3)
Check with FOIL method.
Answer:
Answer in picture
Step-by-step explanation:

In the formula for area of a rectangle A=bh solve for h
Answers
Hi there!
»»————- ★ ————-««
I believe your answer is:
\(h =\frac{A}{b}\)
»»————- ★ ————-««
Here’s why:
⸻⸻⸻⸻
\(\boxed{\text{Solving for 'h'...}}\\\\A=bh\\----------\\\rightarrow bh = A\\\\\rightarrow \frac{bh=A}{b}\\\\\rightarrow \boxed{h=\frac{A}{b}}\)
⸻⸻⸻⸻
»»————- ★ ————-««
Hope this helps you. I apologize if it’s incorrect.
HELP ASAP PLS PLS PLS

Answers
Answer: vertical
Step-by-step explanation:
Answer: its A
Step-by-step explanation:
Divide f(x) by d(x). Your answer
should be in the following format:
f(x)
d(x)
f(x)
d(x)
=
=
Q(x) +
R(x)
d(x)
x³ + 2x² - 72x - 28
x-8
R(x) = [?]
Only enter the R(x) term.
Answers
The value of R(x) term is 36.
We are given that;
The equation x³ + 2x² - 72x - 28
Now,
We divide the first term, 8x, by the first term of d(x), which is x. This gives us 8, which is the third term of Q(x). We write 8 above the division bar and multiply it by d(x), which gives us 8x - 64. We subtract this from the new dividend, which gives us 36.
Since we cannot divide 36 by x-8 any further, we stop here and write 36 as the remainder R(x).
x² + 10x + 8
_______________
x-8 | x³ + 2x² - 72x - 28
- (x³ - 8x²)
-------------
10x² - 72x
- (10x² -80x)
-------------
8x -28
- (8x -64)
----------
36
Q(x) = x² + 10x + 8 and R(x) = 36.
Therefore, by the equation the answer will be R(x) = 36.
To learn more about equations :
brainly.com/question/16763389
#SPJ1
Please answer by today, I'll give brainliest when I can. Help is appreciated!

Answers
Answer:
b = 16.5; 13; 9.5; 6; 2.5
Step-by-step explanation:
Subscribe the given information to get an Answer.
b = 39 / 2 - 3 = 16.5
b = 32 / 2 - 3 = 13
b = 25 / 2 - 3 = 9.5
b = 18 / 2 - 3 = 6
b = 11 / 2 - 3 = 2.5
The points (6, 9) and (5, 8) fall on a particular line. What is its equation in slope-intercept form?
Answers
Answer:
y=x+3
Step-by-step explanation:
Start with the slope equation \(\frac{y_{2} -y_{1} }{x_{2} -x_{1} }\)
Since the first point is actually further along the x-axis that x-value becomes \(x_{2}\) and its corresponding y-value is \(y_{2}\)
\(\frac{9-8}{6-5}\)=\(\frac{1}{1}\)
The slope for the equation is just one so now find the y-intercept by rearranging the slope-intercept equation.
y=mx+b
y-mx=b
Now Substitute either point in to find b
9-1(6)=b
9-6=b
b=3
Your y-intercept is 3 so now we can write the slope-intercept equation for the two points:
y=x+3
What the answer to this one

Answers
Answer:
7=-5
Step-by-step explanation:
7=-5
Simplfy the answer t-4t2/t2

Answers
Answer:
t - 16
Step-by-step explanation:
Hope this helps!! :))
x - 3y = 17
x = 2y + 13
What are the steps for solving these?
Answers
Answer:
(x, y) = (5, -4)
Step-by-step explanation:
The second equation gives you an expression for x that can be substituted into the first equation.
(2y +13) -3y = 17 . . substitute for x in the first equation
-y = 4 . . . . . . . . . . . subtract 13 and simplify
y = -4
x = 2(-4) +13 = 5 . . . use the second equation to find the value of x
The solution is (x, y) = (5, -4).
_____
Additional comment
When faced with a system of linear equations, the first step is to look at them and observe where the variable terms are, and any relationships between coefficients. Several options are generally open to you for solving the equations. Methods generally taught first are ...
substitutioneliminationSubstitution is handy when one of the variables or variable terms can be written (easily) in terms of the other variable. Elimination is handy when some simple multiple of one of the equations can be added to the other equation to cancel one of the variable terms (eliminate it).
Other available methods include matrix methods, Cramer's rule, and graphing. Working knowledge of all of these methods will help you identify the one that will be easiest to use in any given situation.
The availability of calculators able to use these methods greatly simplifies the task of finding a solution. It is simply a matter of entering the equations in the appropriate form.
One of my favorites is the graphing calculator, which only requires you type in the given equations and click on the solution point to find its coordinates.

Quadrilateral WXYZ will be rotated 180° about the origin and then reflected across the Y axis. Choose all of the statements about the quadrilateral and/or the transformed quadrilateral that are correct.
Answers
Answer:
The quadrilaterals will be congruent
The quadrilateral will now appear in Quadrant 2
Step-by-step explanation:
Given
\(W = (-7,-2)\)
\(X= (-4,-2)\)
\(Z = (-6,-6)\)
\(Y =(-3,-7)\)
Rotation across 180 degrees
Reflection across y-axis
Required
The true statement
Using point W as a point of reference; We have:
\(W = (-7,-2)\)
1. Rotation across 180 degrees
The rule is:
\((x,y) \to (-x,-y)\)
So:
\(W(-7,-2) \to W'(7,2)\)
2. Reflection across y-axis
The rule is:
\((x,y) \to (-x,y)\)
So:
\(W'(7,2) \to (-7,2)\)
Using the above transformation on the other points; We have:
\(W(-7,-2) \to W"(-7,2)\)
\(X (-4,-2) \to X "(-4,2)\)
\(Z (-6,-6) \to Z" (-6,6)\)
\(Y(-3,-7) \to Y"(-3,7)\)
Plot the above points on a grid (see attachment).
From the grid, we can conclude that: the quadrilaterals will be congruent , and it will appear in Quadrant 2.

Answer:
what the guy above me said
Step-by-step explanation:
i copied his answer got it right
CAN SOMEBODY HELP ME WITH THIS?????? I WILL MARK BRAINLIEST
CAN SOMEBODY HELP ME WITH THIS?????? I WILL MARK BRAINLIEST

Answers
Answer:
2/7 or about 29%
Step-by-step explanation:
2 are blue and there are 7 cards total so 2/7 and 2 divided by 7 is .2857 or .29 (29%).
Answer:
2/7
Step-by-step explanation:
There are 7 envelopes and 2 blue envelopes so the probability that the envelope will be blue is 2/7
Type in the value of y.
If x = 7, then y =
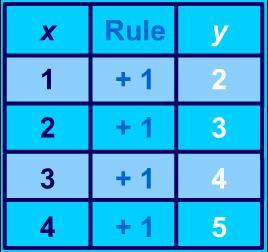
Answers
Explanation:
The rule says "whatever x is, add 1 to it to get y"
So for instance, if x = 3, then y = x+1 = 3+1 = 4
Now if x = 7, then y = x+1 = 7+1 = 8
Answer:
\(\huge\boxed{Answer\hookleftarrow}\)
Given that,
\(1 + 1 = 2 \\ 2 + 1 = 3 \\ 3 + 1 = 4 \\ 4 + 1 = 5...\)
So from this we can infer that, \(\large\bold{ x + 1 = y}\)
Now,
\(x = 7 \\ y= \: ?\)
Use the rule ⎆ \(\large\bold{ x + 1 = y}\)
\(x + 1 = y \\ 7 + 1 = y \\ 8 = y\)
✐ The value of y is 8.
ʰᵒᵖᵉ ⁱᵗ ʰᵉˡᵖˢ
# ꧁❣ RainbowSalt2²2² ࿐
The monthly cost of driving a car depends on the number of miles driven. Lynn found that in May it cost her $356 to drive 380 mi and in June it cost her $404 to drive 620 mi. The function is C(d)=0.2+280 (b) Use part (a) to predict the cost of driving 1800 miles per month. (c) Draw a graph (d) What does the slope represent? What does the C-intercept represent? Why does a linear function give a suitable model in this situation?
(b) $640 (c) y-int of 280, positive slope (d) It represents the cost (in dollars) per mile. It represents the fixed cost (amount she pays even if she does not drive). A linear function is suitable because the monthly cost increases as the number of miles driven increases.
Answers
To predict the cost of driving 1800 miles per month, substitute 1800 in the given function C(d) = 0.2d + 280C(1800) = 0.2 (1800) + 280= $640 per month. Therefore, the cost of driving 1800 miles per month is $640.
(b) Graph is shown below:(c)The slope of the graph represents the rate of change of the cost of driving a car per mile. The slope is given by 0.2, which means that for every mile Lynn drives, the cost increases by $0.2.The y-intercept of the graph represents the fixed cost (amount she pays even if she does not drive).
The y-intercept is given by 280, which means that even if Lynn does not drive the car, she has to pay $280 per month.The linear function gives a suitable model in this situation because the monthly cost increases as the number of miles driven increases.
This is shown by the positive slope of the graph. The fixed cost is also included in the function, which is represented by the y-intercept. Therefore, a linear function is a suitable model in this situation.
To know more about function visit:
https://brainly.com/question/31062578
#SPJ11s.
3 (x + y) -5 (x - y)
Answers
Answer:
-2x - 2y
Step-by-step explanation:
I am not sure what this is asking so here we go...
3(x + y ) - 5(x + y)
3x + 3y - 5x - 5y
-2x - 2y
The College Board states that the average math SAT score is 514 with a standard deviation of 117. Colleen gathered data from 50 students in her graduating class and found the average score to be 523. She thinks that her class’s math SAT score is different from the average. Which of the following are the correct null hypothesis and alternate hypothesis? H0: Mu = 514; Ha: Mu greater-than 514 H0: Mu not-equals 514; Ha: Mu = 523 H0: Mu = 514; Ha: Mu not-equals 514 H0: Mu = 514; Ha: Mu = 523.
Answers
From the hypothesis test, we have that:
The null hypothesis is \(H_0: \mu = 514\).The alternative hypothesis is: \(H_1: \mu \neq 514\)At the null hypothesis, it is tested if her average is the same as the national of 514, hence:
\(H_0: \mu = 514\)
At the alternative hypothesis, it is tested if it is different, hence:
\(H_1: \mu \neq 514\)
A similar problem is given at https://brainly.com/question/24330815
Answer:
c
just took on edge
\
Step-by-step explanation:
Use the information given to answer the question.
Jim, Kimora, and Lonnie are traveling to colleges from each of their respective houses. All the students travel at average rates of 55 mph. These functions are based on Jim and Kimora's distance to their house.
f(x)=140-55x
g(x)=220-55x
The distance Jim travels to college is
140 miles. The distance Kimora travels to college is 220 miles.
If Jim and Kimora begin their travel at the same time, which function represents Kimora’s travel based on Jim’s travel?
A. g(x)=f(x-20)
B. g(x)=f(x+80)
C. g(x)=f(x)-20
D. g(x)=f(x)+80
Then based on your answer choice, Lonnie and Kimora live the same distance from their respective colleges and travel at the same rate. If Lonnie leaves two hours before Kimora, which function represents Lonnie’s travel, h(x), based on Kimora’s travel?
A. h(x)=g(x+2)
B. h(x)=g(x-2)
C. h(x)=g(x)+2
D. h(x)=g(x)-2
Topic: Algebra 2 functions.
Answers
Comparing the functions, it is found that:
The function Kimora's travel based on Jim's travel is of: D. g(x) = f(x) + 80.Lonnie's function based on Kimora is: B. h(x) = g(x - 2).-----------------------------------------
Jim's equation is of:
\(f(x) = 140 - 55x\)
Kimora's equation is of:
\(g(x) = 220 - 55x\)
The -55x term is common to both functions, while the constant on g is 80 more than f, thus:
\(g(x) = f(x) + 80\)
Which means that the answer to the first question is given by option D.
Lonnie started traveling two hours before Kimora's, using the same equation of motion, just with the input x reduced by 2, thus:
\(h(x) = g(x - 2)\)
Which means that the answer to the second question is given by option B.
A similar problem is given at https://brainly.com/question/24759429
A 3-column table with 4 rows. Column 1 is labeled Rectangle with entries A, B, C, D. Column 2 is labeled Width with entries 3 feet, 6 feet, 15 feet, 60 feet. Column 3 is labeled Length with entries 5 feet, 10 feet, 25 feet, 90 feet. Which rectangle is not an enlargement of rectangle A? A B C D
Answers
Answer:
The answer is d
Step-by-step explanation:
Answer:
it D
Step-by-step explanation:
hope it helps
The coordinates of the vertices of XYZ are
X(0, –4), Y(0, 0), and Z(3, 3).
a) Determine the coordinates of the image
of AXTZ after the translation [3, -2].
Answers
Answer:
Step-by-step explanation:

Use the table to work out the values of a , b , c , and d. X y = 2 x + 1 − 3 a − 2 − 3 − 1 b 0 1 1 c 2 d a = b = c = d =
Answers
By Using the table to work out the values of a , b , c , and d. X y = 2 x + 1 − 3 a − 2 − 3 − 1 b 0 1 1 c 2 d a = b = c = d =
Therefore, The solutions are : a = -3, b = 0, c = 6, d = 9
Equation:
In mathematics, an equation is an expression that indicates equality of two expressions by connecting them with the equal sign = . The word "equation" and related words in other languages can have slightly different meanings. For example, in French an equation is defined as containing one or more variables, whereas in English a well-formed formula consisting of two expressions connected by an equal sign is an equation.
Given:
This table;
x y = 3x+3
-3 -6
-2 a
-1 b
0 3
1 c
2 d
To Find:
Values of a, b, c and d
Consider the 2nd row,
x = -2, y = a
Putting the values in the equation,
we get,
a = 3(-2) + 3
⇒ a = -3
Consider the 3rd row,
x = -1, y = b
Putting the values in the equation,
we get,
b = 3(-1) + 3
⇒ b = 0
Consider the 5th row,
x = 1, y = c
Putting the values in the equation,
c = 3(1) + 3
⇒ c = 6
Consider the 6th row,
x = 2, y = d
d = 3(2) + 3
⇒ d = 9
The final answer is,
a = -3, b = 0, c = 6, d = 9.
Learn more about solutions:
https://brainly.com/question/29263728
#SPJ4