intuitively, what do we expect to have when the sample size increases when we estimate a simple linear regression model?

The greatest common factor (GCF) of the expression 9a^6 - 27a^3b^3 + 45a^5b is 9a^3. Factoring out the GCF gives us 9a^3(a^3 - 3b^3 + 5ab).

To factor out the greatest common factor (GCF), we need to identify the largest common factor that can be divided evenly from each term of the expression.

Let's analyze each term individually:

Term 1: 9a^6

Term 2: -27a^3b^3

Term 3: 45a^5b

To find the GCF, we need to determine the highest exponent of a and b that can be divided evenly from all the terms. In this case, the GCF is 9a^3.

Now, let's factor out the GCF from each term:

Term 1: 9a^6 ÷ 9a^3 = a^3

Term 2: -27a^3b^3 ÷ 9a^3 = -3b^3

Term 3: 45a^5b ÷ 9a^3 = 5ab

Putting it all together, we have:

9a^6 - 27a^3b^3 + 45a^5b = 9a^3(a^3 - 3b^3 + 5ab)

Therefore, after factoring out the GCF, the expression becomes 9a^3(a^3 - 3b^3 + 5ab).

Learn more about highest exponent here:

brainly.com/question/30552488

#SPJ11

To set up a partial fraction decomposition for a rational expression, we want to express it as a sum of simpler fractions, with each denominator being a linear factor (i.e. a factor of the form ax + b, where a and b are constants). The general form of a partial fraction decomposition is:

f(x) = A/(ax + b) + B/(cx + d) + ...

where A, B, etc. are constants that we'll need to solve for.

Note that we're not trying to find specific values for A, B, etc. in this question - we're just setting up the decomposition.

So, for each rational expression, we'll need to factor the denominator into linear factors (if it's not already in that form). Then we'll set up the partial fraction decomposition using the formula above. Here are a few examples:

Example 1: (x^2 + 5x + 6)/(x^2 + 4x + 3)

First, let's factor the denominator: x^2 + 4x + 3 = (x + 1)(x + 3). So we can write:

(x^2 + 5x + 6)/(x^2 + 4x + 3) = A/(x + 1) + B/(x + 3)

Note that we have two linear factors in the denominator, so we need two terms in the partial fraction decomposition. We don't know what A and B are yet - we'll need to solve for them.

Example 2: (2x + 5)/(x^2 - 4)

The denominator here is not yet in factored form, so we'll need to factor it first: x^2 - 4 = (x + 2)(x - 2). Then we can write:

(2x + 5)/(x^2 - 4) = A/(x + 2) + B/(x - 2)

Again, we have two linear factors in the denominator, so we need two terms in the partial fraction decomposition.

Example 3: (4x^2 - 2x + 1)/(x^3 + x)

The denominator here is not in factored form, so we'll need to factor it: x^3 + x = x(x^2 + 1). Then we can write:

(4x^2 - 2x + 1)/(x^3 + x) = A/x + B/(x^2 + 1)

In this case, we have one linear factor (x) and one quadratic factor (x^2 + 1), so we need two terms in the partial fraction decomposition.

Learn more about decomposition here:

https://brainly.com/question/8009068

#SPJ11

Answer:

7.625597485 DFNFNFJFKJFKF

Answer:

B

Step-by-step explanation:

given that x and y vary inversely then the equation relating them is

y = \(\frac{k}{x}\) ← k is the constant of variation

to find k use the condition y is 24 when x is 8 , then

24 = \(\frac{k}{8}\) ( multiply both sides by 8 to clear the fraction )

192 = k

y = \(\frac{192}{x}\) ← equation of variation

when y = 18 , then

18 = \(\frac{192}{x}\) ( multiply both sides by x )

18x = 192 ( divide both sides by 18 )

x = \(\frac{192}{18}\) = \(\frac{32}{3}\)

Answer:

Step-by-step explanation:

Write the inverse variation

y = k/x

Solve for k

y = 24

x = 8

y = k/x           Substitute the givens into this equation

24 = k/8        Multiply both sides by 8

8*24 = k

k = 192

Solve for x  when y = 18

y = k/x            Multiply both sides by x

xy = k             Divide by y

x = k/y

x = 192/18

x = 10 2/3       The answer is given as an improper fraction.

x = (10*3 + 2)/3

Answer: x = 32/3

The probability that x is less than 5 = 0.45

Discrete probability distribution:

It is a type of probability distribution that displays all the possible values of a discrete random variable accompanying the affiliated probabilities. We can also say that a discrete probability distribution provides the chance of occurrence of every possible value of a discrete random variable.

Discrete probability distribution:

x          = -10      0       10        20

P(X=x) = 0.35  0.10   0.15     0.40

The probability that x is less than 5:

P(X<5) = 1 - P (X = 10) - P(X= 20)

1 - 0.15 - 0.40 = 0.45

The probability that x is less than 5 is = 0.45

Learn more about probability from:

https://brainly.com/question/23017717

#SPJ4

the equation formula y=2/3x+5 is (3,-3).

Algebraically speaking, an equation is a statement that shows the equality of two mathematical expressions. For instance, the equation 3x + 5 = 14 consists of the two equations 3x + 5 and 14, which are separated by the 'equal' sign.

based on the available facts;

You might be wondering how, but we can start with that 5 at the end, which denotes the y-intercept.

If 0 is used in place of x, then y=2/30+5y=5

We shall receive the first coordinate as a result, which is (0,5).

Let's then consider the slope, which is 2,3. As you may already be aware, the slope is also known as

rise/run

; what do they mean by that is that the first top number tells you how many units you go up and the second one how many units you go right or how many units you go down and go left.

Now, I know this may seem complicated but let's make it clear. Since we know one coordinate, which is

(0,5)

, from that point by knowing the slope we can find a second point; this point is 2 points above and 3 to the right, which tells us that −5+2

points above gives us −3 and 3 points on the right gives us a new coordinate:

(3,−3)

And since we now know two coordinates, that is enough to draw the line and have the graph.

to know more about equation visit;

https://brainly.com/question/14933717

#SPJ9

Answer:

I agree.

Step-by-step explanation:

Where I am, our parents had a choice, to chose whether they wanted us to go back to school or to do it online, and my grandma has me down for online, and I hate it so much.

Hypothesis testing would help evaluate the validity of President Trump's belief by providing statistical evidence to support or reject the claim of widespread illegal voting.

In a similar fashion to the legal analogy example, hypothesis testing can be used to examine President Donald Trump's belief that 3 to 5 million people voted illegally in the presidential election.

To conduct a hypothesis test, we can define the null hypothesis (H0) and the alternative hypothesis (Ha). In this case, the null hypothesis would be that there is no significant illegal voting, while the alternative hypothesis would be that there is significant illegal voting.

Next, we would collect data on voting records, investigate cases of potential illegal voting, and analyze the data to determine if it provides evidence for or against the null hypothesis. Statistical techniques such as sampling, data analysis, and inferential statistics can be utilized to test the hypothesis.

For example, we could randomly sample a subset of voting records and compare them against various criteria to identify any potential instances of illegal voting. Based on the results, we can calculate test statistics and p-values to determine if the evidence supports or refutes the claim of illegal voting.

Ultimately, hypothesis testing would help evaluate the validity of President Trump's belief by providing statistical evidence to support or reject the claim of widespread illegal voting.

For more questions on Hypothesis

https://brainly.com/question/29576929

#SPJ8

The smallest possible value of (a+b) is 2, and this value is attained when a = 1 and b = 1.

Let r and s be the roots of the equation x^2 + ax + 2b = 0, and let p and q be the roots of the equation x^2 + 2bx + a = 0. Since both equations have real roots, their discriminants are nonnegative:

a^2 - 8b ≥ 0

4b^2 - 4a ≥ 0

Simplifying the second inequality, we get:

b^2 - a ≥ 0

b^2 ≥ a

We want to minimize (a+b). Adding the two given equations, we get:

(x^2 + ax + 2b) + (x^2 + 2bx + a) = 0

2x^2 + (a+2b+2b)x + (a+2b) = 0

This equation has real roots if and only if its discriminant is nonnegative:

(a+2b+2b)^2 - 8(2x^2)(a+2b) ≥ 0

(a+4b)^2 - 16b(a+2b) ≥ 0

a^2 + 8ab + 12b^2 ≥ 0

This inequality is always true for positive a and b, so we can safely assume that a and b are positive. Therefore, we can divide both sides by 4b^2 to get:

(a/b)^2 + 8(a/b) + 12 ≥ 0

Letting t = a/b, we can rewrite this as a quadratic inequality:

t^2 + 8t + 12 ≥ 0

This inequality is true for all values of t, so there are no restrictions on the ratio a/b. Therefore, we can minimize (a+b) by choosing a and b to be as small as possible subject to the constraint that b^2 ≥ a. Since a and b are both positive, we can take a = 1 and b = 1 to achieve this minimum. This gives:

(a+b) = 1+1 = 2

Therefore, the smallest possible value of (a+b) is 2, and this value is attained when a = 1 and b = 1.

Learn more about :

real roots : brainly.com/question/30288169

#SPJ11

If a group consists of 10 kids and 2 adults, the number of ways are there to form the line are 2 * 10!. So, correct option is C.

To form a line with an adult at the front and an adult at the back, we need to consider the positions of the 10 kids within the line. The two adults are fixed at the front and back, so we have 10 positions available for the kids.

To calculate the number of ways to arrange the kids in these positions, we can use the concept of permutations. Since each position can be occupied by a different kid, we have 10 options for the first position, 9 options for the second position, 8 options for the third position, and so on, until the last position, where only 1 kid remains.

Therefore, the number of ways to form the line is:

10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 10!

However, the problem also mentions that there are 2 adults, so we need to consider the arrangements of the adults as well. Since there are only two adults, there are 2 ways to arrange them in the line (adult at the front and adult at the back or vice versa).

Therefore, the total number of ways to form the line is:

2 x 10! = 2 * 10!

Hence, the correct option is b. 2 * 10!, which accounts for both the arrangements of the kids and the adults.

To learn more about permutations click on,

https://brainly.com/question/19426809

#SPJ4

Solutions for the system of equations  2x −5y =1  , 4x −10y =3 has no solution as ( 2 /4 ) = (-5/-10) ≠ (1/3) .

Simplify the system of equations to get the solution of the system :

2x - 5y = 1

⇒ 2x = 1 + 5y

⇒ x = ( 1+ 5y ) / 2  __(1)

4x -10y = 3

⇒ 2 ( 2x - 5y ) = 3

⇒2x - 5y = 3/2  ___(2)

Standard form of the system of equations are :

a₁x + b₁y + c₁ = 0

a₂x + b₂y + c₂ = 0

Substitute the value of x from (1) into (2) we get,

2 ( 1 + 5y )/2  - 5y = 3/2

⇒1 + 5y -5y = 3/2

⇒1 = 3/2

⇒2 = 3 which is not true.

System of the equation has no solution.

Here, ( a₁ /a₂ ) = (b₁ /b₂) ≠ (c₁ /c₂ ) that is ( 2 /4 ) = (-5/-10) ≠ (1/3) .

Therefore, the system of equations has no solution.

Learn more about system of equations here

brainly.com/question/12895249

#SPJ4

Solving this quadratic equation for s will give us the possible values for s. Once we have the values of s, we can substitute them back into the first equation (t = 6 - s) to find the corresponding values of t.

what is point of intersection?

The point of intersection refers to the coordinates where two or more curves, lines, or objects intersect or meet. It represents the common point(s) shared by the different entities. In mathematics, finding the point(s) of intersection involves solving equations or systems of equations to determine the values of the variables that satisfy the conditions for intersection.

To find the point of intersection between the curves r1(t) = (t, 4 - t, 24t^2) and r2(s) = (6 - s, s - 2, s^2), we need to equate the corresponding components of the two curves and solve the resulting system of equations.

For the x-component:

t = 6 - s

For the y-component:

4 - t = s - 2

For the z-component:

\(24t^2 = s^2\)

Now, let's solve these equations to find the values of t and s at the point of intersection.

From the first equation, we have:

t = 6 - s

Substituting this into the second equation, we get:

4 - (6 - s) = s - 2

4 - 6 + s = s - 2

-2 + s = s - 2

s cancels out, giving -2 = -2.

This shows that s can have any value since it cancels out from the equation. Therefore, the value of s is not determined uniquely.

Now, let's use the value of t obtained from the first equation to find the z-component using the third equation:

\(24t^2 = s^2\)

\(24(6 - s)^2 = s^2\)

Expanding and simplifying:

\(24(36 - 12s + s^2) = s^2\)

\(864 - 288s + 24s^2 = s^2\)

\(24s^2 + 288s - s^2 = 864\)

\(23s^2 + 288s - 864 = 0\)

Solving this quadratic equation for s will give us the possible values for s. Once we have the values of s, we can substitute them back into the first equation (t = 6 - s) to find the corresponding values of t.

Unfortunately, without solving the quadratic equation or providing additional information, we cannot determine the specific values of (x, y, z) at the point of intersection.

To klnow more about point of intersection visit:

https://brainly.com/question/29185601

#SPJ4

BODMAS Rule :

The BODMAS rule is arranged according to the letters in the acronym BODMAS, which stand for brackets, order of powers or roots, division, and multiplication. A stands for addition and S for subtraction. According to the BODMAS rule, multi-operator mathematical expressions must be resolved in the BODMAS order from left to right.

Given expression :

(11 - 3 x 12) + ( 15 × 11 )

First, we will work on the bracket, our expression becomes,

= (11 - 3 x 12) + 165

Further on solving inside the bracket, by applying multiplication operator, then subtraction operator and finally the addition operator , our expression becomes,

= ( 11 - 36 ) + 165

= -25 + 165

=  140 .

To know more about BODMAS rule, visit,

https://brainly.com/question/25434305

#BODMAS rule

Answer:

Step-by-step explanation:

One pump will fill 200l in 20 minutes

So the rate of filling per pump will be 10l/minute (200/20)

Let the number of minutes it will take to fill the 600l be x minutes

Now, since the rate of filling per pump is 10 l/minute

Then in x minute, they would have filled 10l/minute * x = 10x liters

So it is now this 10x liters that will be equal to 600

To find x, we simply divide

10x = 600

x= 600/10

x = 6 minutes

1. The minimum area occurs when the tangent line is horizontal, which happens at x = 0.5.

2. The minimum area occurs at the starting point, x = 0.

To determine for which non-vertical tangent line the area between the graph of a function f and the tangent line is minimal, we need to consider the relationship between the function and its derivative.

Let's choose three different nonlinear functions and analyze their tangent lines to find the one that minimizes the area between the graph and the tangent line.

1. Function: f(x) = x^2

  Derivative: f'(x) = 2x

  Tangent line equation: T(x) = f'(a)(x - a) + f(a)

  The derivative of f(x) is 2x, and since it is a linear function, it represents the slope of the tangent line at every point. Since the slope is increasing with x, the tangent line becomes steeper as x increases.

Therefore, as we move along the interval [0, 1], the area between the of f(x) and the tangent line gradually increases. The minimum area occurs at the starting point, x = 0.

2. Function: f(x) = sin(x)

  Derivative: f'(x) = cos(x)

  Tangent line equation: T(x) = f'(a)(x - a) + f(a)

  The derivative of f(x) is cos(x). In this case, the tangent line equation depends on the chosen point a. As we move along the interval [0, 1], the slope of the tangent line oscillates between -1 and 1. The minimum area occurs when the tangent line is horizontal, which happens at x = 0.5.

3. Function: f(x) = e^x

  Derivative: f'(x) = e^x

  Tangent line equation: T(x) = f'(a)(x - a) + f(a)

  The derivative of f(x) is e^x, which is always positive. Therefore, the tangent line always has a positive slope. As we move along the interval [0, 1], the tangent line becomes steeper, resulting in an increasing area between the graph of f(x) and the tangent line. The minimum area occurs at the starting point, x = 0.

From these examples, we can make a conjecture: For a concave-up function on the interval [0, 1], the area between the graph of the function and its tangent line is minimized at the starting point of the interval. This is because the tangent line at that point has the smallest slope compared to other tangent lines within the interval.

To verify this conjecture, we can try other concave-up functions and observe if the minimum area occurs at the starting point.

Visit here to learn more about area brainly.com/question/16151549

#SPJ11

Answer:

141

39

141

Step-by-step explanation:

1: 180-39= 141

2: Same as the given angle= 39

3: Same as angle 1= 141

Answer:

i believe the answer is 174.

Step-by-step explanation:

E(U) = 1 , Var(U) = 88.

The independent random variables are X and Y where E(X) = 3, Var(X) = 10, E(Y) = 6, and Var(Y) = 20.

We need to find E(U) and Var(U) where U = 2X - Y + 1.

Find the value of E(U):

Using the formula,E(U) = E(2X - Y + 1) ...equation (1)

Let's calculate each component separately:

E(2X) = 2E(X) {since E(aX) = aE(X)}∴ E(2X) = 2 x 3 = 6E(-Y) = -E(Y) {since E(-X) = -E(X)}∴ E(-Y) = -6E(1) = 1 {since E(constant) = constant}

Putting values in equation (1), we get: E(U) = E(2X - Y + 1)E(U) = E(2X) - E(Y) + E(1)E(U) = 6 - 6 + 1∴ E(U) = 1

Therefore, E(U) = 1.

Var(U) = Var(2X - Y + 1) ...equation (2)

Using the formula,Var(aX + bY) = a²Var(X) + b²Var(Y) + 2abCov(X,Y) {where Cov(X,Y) = ρxy x σx x σy}E(aX + bY) = aE(X) + bE(Y)

Putting values in equation (2), we get:

Var(U) = Var(2X - Y + 1)Var(U) = Var(2X) + Var(-Y) + Var(1) + 2Cov(2X, -Y) + 2Cov(-Y, 1) + 2Cov(2X, 1){Since covariance of independent random variables is zero}

Var(U) = 4Var(X) + Var(Y) + 2Cov(2X, -Y) + 2Cov(-Y, 1) + 4Cov(X,1)Var(U) = 4 x 10 + 20 + 2Cov(2X, -Y) - 2Cov(Y, 1) + 4Cov(X,1){Since covariance of independent random variables is zero}

Var(U) = 60 + 2Cov(2X, -Y) - 4Cov(Y, 1)

Note that, for independent random variables, Cov(X, Y) = 0

Hence,Var(U) = 60 + 2Cov(2X, -Y) - 4Cov(Y, 1){Now, let's calculate Cov(2X, -Y)}

Using the formula,Var(aX + bY) = a²Var(X) + b²Var(Y) + 2abCov(X,Y)Var(2X - Y) = 4Var(X) + Var(Y) - 4Cov(X,Y)

Let's solve for Cov(X,Y)4Var(X) + Var(Y) - 4Cov(X,Y) = Var(2X - Y)4 x 10 + 20 - 4Cov(X,Y) = 4 x 10 - 20Cov(X,Y) = 15

We have the values of Var(X), Var(Y), and Cov(X, Y) in the equation (2).

Let's substitute the values in equation (2).

Var(U) = 60 + 2 x 15 - 4Cov(Y, 1)Var(U) = 90 - 4Cov(Y, 1)

But, we need to calculate the value of Cov(Y,1) {since it is not zero for independent random variables}

Using the formula,Var(aX + bY) = a²Var(X) + b²Var(Y) + 2abCov(X,Y)Cov(X,Y) = [Var(aX + bY) - a²Var(X) - b²Var(Y)]/ 2ab

We need to find Cov(Y, 1)Let a = 1 and b = 1

Using the formula,Cov(Y, 1) = [Var(Y + 1) - Var(Y) - Var(1)]/ 2Cov(Y, 1) = [Var(Y) + Var(1) + 2Cov(Y,1) - Var(Y) - 0]/ 2Cov(Y, 1) = 1 + Cov(Y, 1)Cov(Y, 1) = 1/2

Now, putting the value of Cov(Y, 1) in the expression for Var(U), we get:Var(U) = 90 - 4Cov(Y, 1)Var(U) = 90 - 4(1/2)Var(U) = 88

Therefore, Var(U) = 88.

To know more about covariance visit:

https://brainly.in/question/13828312

#SPJ11

The value of simplified form of the expression is,

⇒ √2 (13 - √3)

We have to given that;

The expression is,

⇒ 3√2-√6+10√2

Now, We can simplify as;

⇒ 3√2 - √6 + 10√2

⇒ 3√2 - √2 × √3 + 10√2

⇒ 13√2 - √2 × √3

⇒ √2 (13 - √3)

Thus, The value of simplified form of the expression is,

⇒ √2 (13 - √3)

Learn more about the mathematical expression visit:

brainly.com/question/1859113

#SPJ1

The correct answer is (C) Yes, because the probability of observing a difference at least as large as the sample difference, if the two population proportions are the same, is less than 0.05.To determine if there is convincing statistical evidence of a difference between the two groups of residents in their opposition to the banning of trans fats, we can conduct a hypothesis test for the difference in population proportions.

The null hypothesis (H0) states that there is no difference between the two population proportions, while the alternative hypothesis (Ha) states that there is a difference.

To conduct the test, we calculate the sample proportions of opposition to the banning of trans fats in each group. In the group with school-age children, the sample proportion is 94/230 = 0.409, and in the group without school-age children, the sample proportion is 147/341 = 0.431.

Next, we calculate the standard error of the difference between the sample proportions using the formula:

SE = sqrt[(p1 * (1 - p1) / n1) + (p2 * (1 - p2) / n2)]

where p1 and p2 are the sample proportions, and n1 and n2 are the sample sizes.

After calculating the standard error, we calculate the test statistic, which follows an approximately normal distribution when the sample sizes are large. The test statistic is given by:

test statistic = (p1 - p2) / SE

Using a significance level of 0.05, we compare the test statistic to the critical value from the standard normal distribution.

If the test statistic falls outside the critical region, we reject the null hypothesis and conclude that there is convincing statistical evidence of a difference between the two population proportions. Otherwise, we fail to reject the null hypothesis.

In this case, the correct answer is (C) Yes, because the probability of observing a difference at least as large as the sample difference, if the two population proportions are the same, is less than 0.05.

To Know more about  null hypothesis Visit:

https://brainly.com/question/33666276

#SPJ11

The program area that is NOT included in the Sigma Phi Delta Efficiency Contest is D. Fraternal Events.

The Efficiency Contest is focused on improving chapter operation through the program areas of Brotherhood Development, Academic Achievement, Pledge Education, Chapter Operations, and Community Service.

The other options (A. Brotherhood Development, B. Academic Achievement, C. Pledge Education, and E. Chapter Operations) are all part of the Efficiency Contest's program areas.

Learn more about "efficiency": https://brainly.com/question/15418098

#SPJ11

Answer:

is tungtset i tink not sure bout

Step-by-step explanation:

mark me brainlest plz

Answer:

48 children

Step-by-step explanation:

For every 5 adults there are 2 children.

so for every 1 adult there is 2/5 of a child.

So number of children = 120 * 2/5

= 240/5

= 48.

The first and second polygons are exactly the same, the only difference is that the second is bigger! If we look right the first polygon is 4 cm and the second is triple which means that we will have to triple the area of ​​the First polygon to discover the area of ​​the second polygon!

if the first polygon is 4 cm long and the second 12 cm means that the second polygon has three times the area of ​​the first polygon!

\((4 cm.3=12 cm)\\A-10 cm^{2}.3=30 cm^{2}\)

the second polygon has \(30 cm^{2}\)  of area

\(A=30 cm^{2}\)

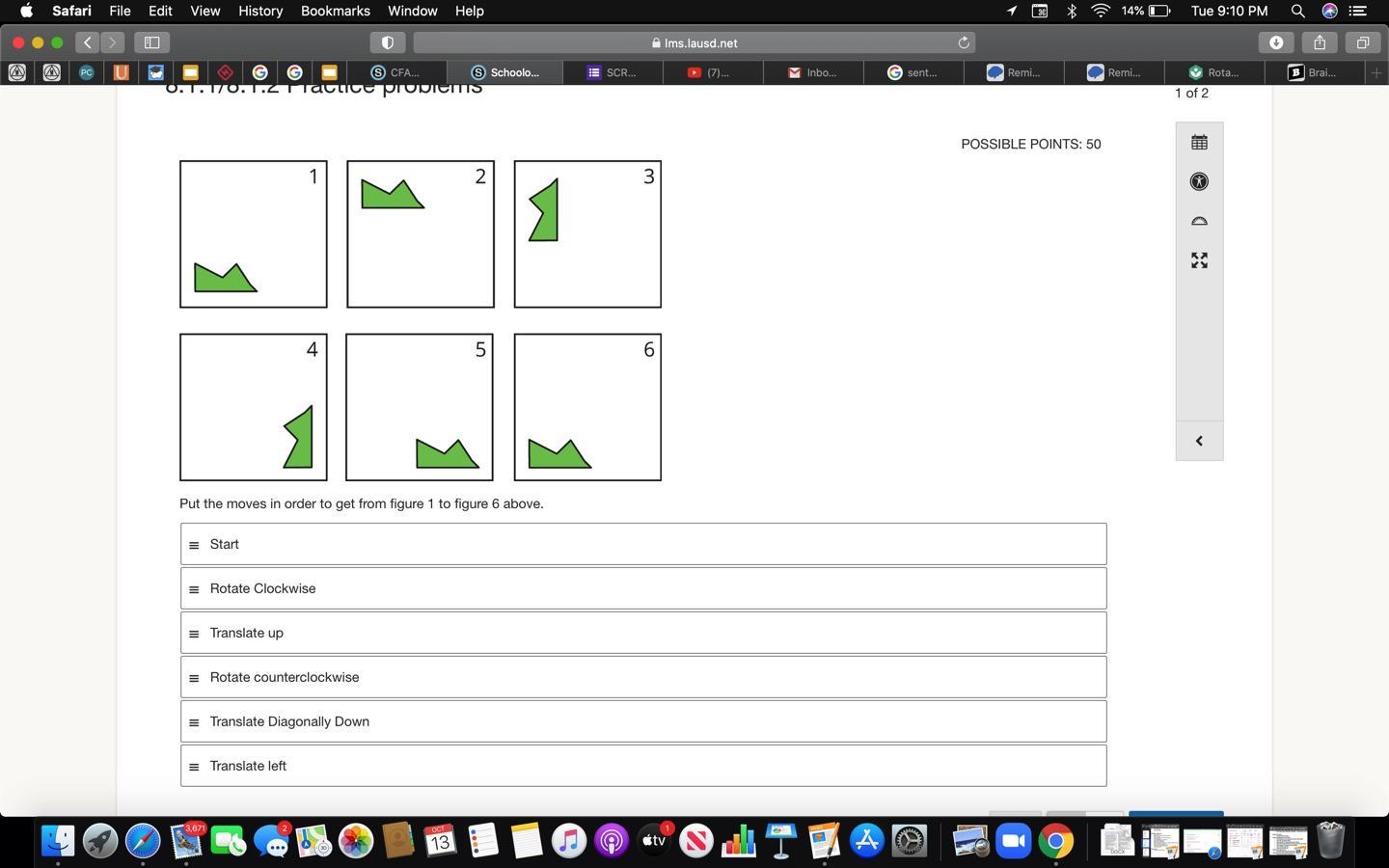
Answer:

Step-by-step explanation:

Start

Translate up

Rotate counter clockwise

Translate diagonally down

Rotate clockwise

Translate left

Answer:

the answer is b

Step-by-step explanation:

8 x 5 gets to 40 then 11 is how much you have

Answer:

Hi friend! The answer is B. 11/5

Answer:

No because their ratios are not the same

Step-by-step explanation:

The scalar from 5 to 10 is 2 but from 3 to 4, its 4/3.