ILL MARK BRAINLIEST!!
The side length of the base of a square pyramid is 30 centimeters. The height of pyramid is 45 centimeters.
What is the volume of the pyramid in cubic centimeters?
A) 13,500 cm3
B) 40,500 cm3
C) 900 cm3
D) 1,350 cm3
Answers
Answer:
13,500 cm³ is the volume
Step-by-step explanation:
plz mark brainliest :D
Related Questions
The table below shows the predicted number of words Janae can type, y, in x minutes. Time (x, in minutes) Words Typed (y) 5 150 10 300 15 450 20 600 Which describes the pattern in the table? A. Janae types 25 words each minute. B. Janae types 30 words each minute. C. Janae types 145 words each minute. D. Janae types 150 words each minute.
Answers
Answer:
(B) 30 words each minute
Step-by-step explanation:
If you take any of the inputs and multiply it by 30 you will get the output of the number you chose
Janae can type 30 words each minute. which is the correct answer would be an option (B)
What are Arithmetic operations?Arithmetic operations can also be specified by adding, subtracting, dividing, and multiplying built-in functions.
/ Division operation: Divides left-hand operand by right-hand operand
For example 4/2 = 2
We have been given that the table indicates the expected number of words Janae can type, y, in x minutes.
Time (x, in minutes) Words Typed (y)
5 150
10 300
15 450
20 600
We have to determine the pattern which describes in the given table.
Words typed (y) divided by time (x, in minutes)
As per the table,
⇒ 150/5 = 30
⇒ 300/10 = 30
⇒ 450/15 = 30
⇒ 600/20 = 30
Therefore, he can type 30 words each minute.
Learn more about Arithmetic operations here:
brainly.com/question/25834626
#SPJ2
Assume that x has a normal distribution with the
specified mean and standard deviation. Find the indicated
probability. (Round your answer to four decimal places.)
= 2.4; = 0.36
P(x ≥ 2) =
Answers
The probability of x being greater than or equal to 2 in a normal distribution with mean μ = 2.4 and standard deviation σ = 0.36 is approximately 0.8664.
How to find the probability in a normal distribution?To find the probability P(x ≥ 2) for a normal distribution with a mean of μ = 2.4 and a standard deviation of σ = 0.36, we can use the standard normal distribution table or a statistical calculator.
First, we need to standardize the value x = 2 using the formula:
z = (x - μ) / σ
z = (2 - 2.4) / 0.36 = -1.1111 (rounded to four decimal places)
Next, we can find the probability P(z ≥ -1.1111) using the standard normal distribution table or a statistical calculator. The table or calculator will provide the cumulative probability up to the given z-value.
P(z ≥ -1.1111) ≈ 0.8664 (rounded to four decimal places)
Therefore, the probability P(x ≥ 2) for the given normal distribution is approximately 0.8664.
Learn more about probability
brainly.com/question/31828911
#SPJ11
The students in Nora's class chose between two options for an assignment. 5/8 of the students chose option 1. If there are 32 students in Nora's class, how many chose option 1?
A. 28
B. 24
C. 20
D. 15
Answers
Answer:
The answer to your problem is, C. 20
Step-by-step explanation:
First, find the decimal of 5/8, which is 0.625. It will be used later.
If you can recall cannot divide a decimal because it will multiply it instead.
We will have to use multiplication because since it is a decimal it is the same as dividing.
32 students, so multiply by 0.625
= 20
Thus the answer to your problem is, C. 20
Your weekly base salary is $150. You earn $20 for each cell phone that
you sell.
a. What is the minimum amount you can earn in a week?
b. Write and solve an inequality that represents the number of cell phones
you must sell to make at least $630 a week.
c. Write and solve an inequality that represents the number of cell phones
you must sell to make at least $750 a week.
d. The company policy is that as a part-time employee, the maximum
you can earn each week is $950. Write and solve an inequality that
represents the number of cell phones you can sell each week.
Answers
The minimum that could be earned is $150. The required inequalities are solved below:
What is an inequality?
An inequality in mathematics is a relationship that makes a non-equal comparison between two integers or other mathematical expressions. It is most commonly used to compare the sizes of two numbers on a number line. There are multiple notations used to denote various types of inequalities: The symbol a b indicates that an is smaller than b. The symbol a > b indicates that an is more than b. In either scenario, a and b are not equal. These are characterized as stringent inequalities because an is either strictly less than or strictly bigger than b. Equivalence is not allowed.
(a) The minimum that could be earned is $150.
(b) The required inequality is given as 150+20x≥630
or, 20x≥630-150
or, x≥480/20
or, x≥24
(c) The required inequality is given as 150+20x≥750
or, 20x≥750-150
or, x≥600/20
or, x≥30
(d) The required inequality is given as 150+20x≤950
or, 20x≤950-150
or, x≤800/20
or, x≤40
To know more about inequalities, click on the link
https://brainly.com/question/25944814
#SPJ9
⚠️⚠️ What’s the slope and intercept B ⚠️⚠️
MARKING BRAINLIEST ASAP

Answers
Answer:
The slope is 1 and the y-intercept is 3.
Step-by-step explanation:
45 % of z is 72. Find the value of z
Answers
9/20z=72
z=72/ 9/20
z=160
Un puente colgante tiene un cable en forma de parábola. El puente se apoya en dos torres. Hay 136 metros de distancia entre las torres. Si el cable está a 17 metros de altura cuando está a 34metros de distancia del centro del puente, ¿cuál es la altura de una de las torres?
Answers
Solve the following proportion: (round to the nearest tenths place if necessary)
4/7=10/x
I need the explanation
Answers
Solution:
Note that:
4/7 = 10/xTo find the solution to the proportion, we will need to simplify the equation (4/7 = 10/x)
4/7 = 10/x=> 4x = 70=> x = 70/4 = 35/2 = 17.5.Hoped this helped!
Answer:
x = 17.5
Step-by-step explanation:
4/7 = 10/x
4x = 70
x = 70/4
x = 17.5
solve the problem with simplex method , and verify using graphical method
4) Min Z = -2X1 - 4X2 - 3X3
St. X1 + 3X2 + 2X3 <= 30 X1 + X2 + X3 <= 24
3X1 + 5X2 + 3X3 <= 60
Xi >= 0
Answers
The problem can be solved using the simplex method, and the solution can be verified using the graphical method. The optimal solution is X1 = 6, X2 = 0, X3 = 6, Z = 24.
The problem can be solved using the simplex method, and verified using the graphical method. Here are the steps:
Convert the problem to standard form by introducing slack variables:
Min Z = -2X1 - 4X2 - 3X3 + 0S1 + 0S2 + 0S3
St. X1 + 3X2 + 2X3 + S1 = 30
X1 + X2 + X3 + S2 = 24
3X1 + 5X2 + 3X3 + S3 = 60
Xi, Si >= 0
Set up the initial simplex tableau:
| 1 3 2 1 0 0 30 |
| 1 1 1 0 1 0 24 |
| 3 5 3 0 0 1 60 |
| 2 4 3 0 0 0 0 |
Identify the entering variable (most negative coefficient in the objective row): X2
Identify the leaving variable (smallest ratio of RHS to coefficient of entering variable): S1
Pivot around the intersection of the entering and leaving variables to create a new tableau:
| 0 2 1 1 -1 0 6 |
| 1 0 0 -1 2 0 18 |
| 0 0 0 5 -5 1 30 |
| 2 0 1 -2 4 0 36 |
Repeat steps 3-5 until there are no more negative coefficients in the objective row. The final tableau is:
| 0 0 0 7/5 -3/5 0 18 |
| 1 0 0 -1/5 2/5 0 6 |
| 0 0 1 1/5 -1/5 0 6 |
| 0 0 0 -2 4 0 24 |
The optimal solution is X1 = 6, X2 = 0, X3 = 6, Z = 24.
To verify the solution using the graphical method, plot the constraints on a graph and find the feasible region. The optimal solution will be at one of the corner points of the feasible region. By checking the values of the objective function at each corner point, we can verify that the optimal solution found using the simplex method is correct.
In conclusion, the problem can be solved using the simplex method, and the solution can be verified using the graphical method. The optimal solution is X1 = 6, X2 = 0, X3 = 6, Z = 24.
Learn more about Graphical method
brainly.com/question/29193266
#SPJ11
To see how to solve an equation that involves the absolute value of a quadratic polynomial, such as 3x4, work Exercises 83-86 in order 83. For x²-3x to have an absolute value equal to 4, what are the two possible values that it may be? (Hint One is positive and the other is negative.) 84. Write an equation stating that x²-3x is equal to the positive value you found in Exercise 83, and solve it using factoring 85. Write an equation stating that x²-3x is equal to the negative value you found in Exercise 83, and solve it using the quadratic formula. (Hint: The solutions are not real numbers) 86. Give the complete solution set of x²-3x =4, using the results from Exercises 84 and 85 83. What are the two possible values of x²-3x? (Use a comma to separate answers as needed.)
Answers
Note that the complete solution set of x²-3x = 4 is x = 4, -1.
How is this so ?To find the two possible values of x²-3x,we need to solve the equation |x²-3x| = 4.
We found that the two possible values are x = 4 and x = - 1.
Using the positive value, we can write the equation x²-3x = 4 and solve it using factoring -
x²-3x - 4 = 0
(x-4)(x+1) = 0
From this, we get two solutions - x = 4 and x = -1.
Using the negative value, we can write the equation x²-3x = -4 and solve it using the quadratic formula -
x²-3x + 4 = 0
Using the quadratic formula - x = (-(-3) ± √((-3)² - 4(1)(4))) / (2(1))
Simplifying, we get - x = (3 ± √(9 - 16)) / 2
Since the discriminant is negative, there are no real solutions. Therefore, there are no real number solutions for x in this case.
Hence, the complete solution set of x²-3x = 4 is x = 4, -1.
Learn more about solution set:
https://brainly.com/question/10588366
#SPJ4
Help!!! I need help I don't know how to do it

Answers
50% of 42 people =21
150% of 42 people=63
Hope it helps : )
SOMEONE PLLLLZZZ HELP MMEEE!!!III BBEEGGGGG UUU!!!!
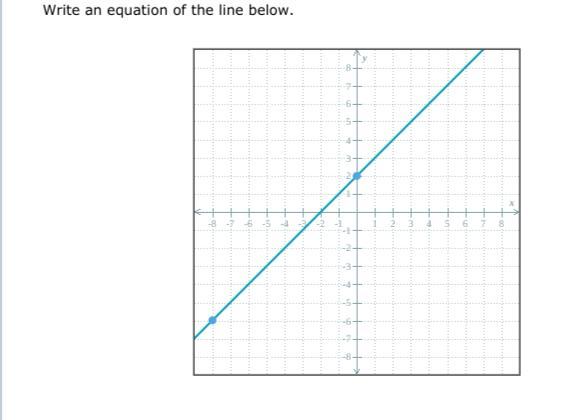
Answers
Answer:
y = x + 2
Step-by-step explanation:
Used slope formula to get a slope of 1
Line crosses y axis at (0,2)
I think. I was just doing this an hour ago. But you are first meant to find the gradient. Then you create the equation.
Read my notes

Assume that TDW Corporation (calendar year-end) has 2022 taxable income of $650,000 for purposes of computing the §179 expense. The company acquired the following assets during 2022: (Use MACRS Table 1, Table 2, Table 3, Table 4 and Table 5. ) Asset Placed in Service Basis Machinery September 12 $ 2,270,000 Computer equipment February 10 263,000 Furniture April 2 880,000 Total $ 3,413,000 a. What is the maximum amount of §179 expense TDW may deduct for 2022?
Answers
The maximum amount of §179 expense TDW may deduct for 2022 is $257,000.
To determine the maximum amount of §179 expense that TDW Corporation can deduct for 2022, we first Add up the cost of all the assets acquired in 2022:
$2,270,000 (machinery) + $263,000 (computer equipment) + $880,000 (furniture) = $3,413,000
Now we determine the amount of the §179 deduction limit for the tax year.
For tax year 2022, the §179 deduction limit is $1,050,000.
Check if the cost of the assets exceeds the §179 deduction limit.
Since the cost of the assets ($3,413,000) is greater than the §179 deduction limit ($1,050,000), we need to calculate the phase-out limit.
Now we determine the phase-out limit.
For tax year 2022, the phase-out limit is $2,620,000.
Calculate the §179 expense deduction.
Since the cost of the assets ($3,413,000) is greater than the phase-out limit ($2,620,000), we need to reduce the §179 deduction by the excess over the phase-out limit.
The excess over the phase-out limit is $793,000 ($3,413,000 - $2,620,000).
The §179 expense deduction is the lesser of the §179 deduction limit and the cost of the assets reduced by the excess over the phase-out limit.
The §179 expense deduction is $1,050,000 - $793,000 = $257,000.
Learn more about Assets at:
brainly.com/question/25746199
#SPJ4
Kimberly is training to swim a 3-mile
race. To practice, she is swimming 9
miles in one week. How many yards
will Kimberly swim that week?
Answers
Answer: 15,840 yards
Step-by-step explanation: First found out how many yards are in a mile: 1760. Then multiply by 1760 by 9. Which will give you 15,840.
BRAINLIEST GOES TO THE CORRECT ANSWER!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
11.99
Step-by-step explanation:
In a pack of Skittles, 20% are red. If 13 are red, how many skittles were in the entire bag?
Answers
Answer: 65
Step-by-step explanation:
First we need to know what the 13 is 20% of. 13 is 20% of 65.
To make sure we are correct we must take 20% of the 65 which gives us 13 showing that 20% of the 65 skittles (13) are red.
Hope that helped :)
Let I and J be ideals and P a prime ideal of R. Prove that if I J ⊆ P then I ⊆ P or J ⊆ P.
Answers
We have shown that if IJ ⊆ P, then either I ⊆ P or J ⊆ P. Hence, the statement is proven, for I and J be ideals and P a prime ideal of R. Since P is prime, so we have the following inequality:(I intersection P) (J intersection P) ⊆ P²
Now, since P is prime so P² is a prime ideal too, thus one of the ideals I intersection P and J intersection P must be contained in P.
If I intersection P ⊆ P, then I ⊆ P. If J intersection P ⊆ P, then J ⊆ P. Therefore, I ⊆ P or J ⊆ P.
To prove the statement, let's assume that I and J are ideals of a ring R, and P is a prime ideal of R. We want to show that if IJ ⊆ P, then either I ⊆ P or J ⊆ P.
Suppose that IJ ⊆ P, We will proceed by contradiction.
Assume that I is not contained in P, which means there exists an element a ∈ I such that a ∉ P.
Since P is a prime ideal, it is closed under multiplication, so aJ ⊆ PJ ⊆ P.
Now consider the product (aJ)(a⁻¹). Since a ∉ P, a⁻¹ ∈ R\P (the complement of P in R).
Therefore, (aJ)(a⁻¹) ⊆ P(a⁻¹), and we have:
aJ ⊆ P(a⁻¹)
Multiplying both sides by a, we get:
a(aJ) ⊆ a(P(a⁻¹))
a²J ⊆ Pa⁻¹
Since J is an ideal, a²J ⊆ aJ ⊆ P(a⁻¹), and by induction,
we have aⁿJ ⊆ Pa⁻ⁿ for any positive integer n.
Consider the element aⁿ ∈ aⁿJ.
Since aⁿJ ⊆ Pa⁻ⁿ, aⁿ ∈ Pa⁻ⁿ.
This implies that aⁿ is an element of the prime ideal P for any positive integer n.
Since R is a ring, there exists a positive integer m such that aᵐ = aᵐ⁺¹ for some m⁺¹ > m.
This means that aᵐ (a - 1) = 0.
Since aᵐ ∈ P and P is a prime ideal, either a or (a - 1) must be in P.
If a is in P, then I ⊆ P, which is one of the conditions we want to prove.
If (a - 1) is in P, then consider the element 1 ∈ R. Since (a - 1) is in P, we have 1 - (a - 1) = a ∈ P.
This implies J ⊆ P, which is the other condition we want to prove.
In either case, we have shown that if IJ ⊆ P, then either I ⊆ P or J ⊆ P. Hence, the statement is proven.
To know more about intersection, visit:
https://brainly.com/question/29185601
#SPJ11
A science test, which is worth 100 points, consists of 24 questions. Each question is worth either 3 poir
points. If x is the number of 3-point questions and y is the number of 5-point questions, the system sho
represents this situation.
x + y = 24
3x + 5y = 100
What does the solution of this system indicate about the questions on the test?
O The test contains 4 three-point questions and 20 five-point questions.
The test contains 10 three-point questions and 14 five-point questions.
O The test contains 14 three-point questions and 10 five-point questions.
O The test contains 20 three-point questions and 8 five-point questions.
Answers
Answer:
The test contains 10 three-point questions and 14 five-point questions.
Step-by-step explanation:
3x + 5y = 100, so:
x - number of 3-point questions
y - number of 5-point questions
x + y = 24 ⇒ y = 24 - x
3x + 5y = 100
3x + 5(24-x) = 100
3x + 120 - 5x = 100
-2x = -20
x = 10
y = 24 - 10 = 14
What is the perimeter of QRST?
__ ft

Answers
Answer:
The perimeter of QRST is 20 ft.
Step-by-step explanation:
Trapizeod EFGH is equal to QRST so that means their permiters are the same.
If the perimeter for EFGH is 20 ft (5 + 4 + 3 +8) so then QRST is 20 ft too. Hope this helps. :)
The Fitzgerald paid $3,200 to heat their home in the year of 2018. By the end of the year 2019, they saw the cost of heating their home rose to $3,516 for the year. What could be use to find the difference in what they paid from 2918-2019?
Answers
Answer:
Substraction
Step-by-step explanation:
Given that
The amount paid in the year 2018 is $3,200
And, in the year 2019 the amount paid is $3,516'
We need to find the differnece between two years so how we can find
Basically we need to subtract the amount i.e.
= $3,516 - $3,200
= $316
hence, the difference is of $316 from 2018 to 2019
Suppose you and your twin have different insurance plans. Your insurance plan has a fixed copay of $40 for each doctor's visit, but your twin's copay is 20% of the total cost. The local dentist charges $150 for a cleaning. Which of the following is most likely true? You will visit the dentist more. Your twin will visit the dentist more. You and your twin will visit the dentist the same number of times. Your twin will switch insurance plans.
Answers
Your twin is likely to visit the dentist more frequently than you due to the difference in insurance plans.
Based on the given information, your insurance plan has a fixed copay of $40 for each doctor's visit, while your twin's copay is 20% of the total cost. Considering the local dentist charges $150 for a cleaning, you would pay a fixed copay of $40 regardless of the total cost. On the other hand, your twin's copay would be 20% of $150, which amounts to $30. Therefore, your twin would have a lower out-of-pocket expense for each dentist visit compared to you.
Due to the lower copay, your twin is more likely to visit the dentist more frequently. The difference in copayments means that your twin would save $10 on each visit, making it more cost-effective for them to seek dental care. This financial advantage would incentivize your twin to take better advantage of their insurance plan and visit the dentist more often.
Based on this reasoning, it is unlikely that you and your twin would visit the dentist the same number of times. Furthermore, there is no indication in the given information that your twin would switch insurance plans, as their plan offers a more favorable copayment structure for dental visits.
Learn more about difference here:
https://brainly.com/question/30241588
#SPJ11
Find 3 consecutive odd integers such that 10 times the first is 59 more than the third
Answers
9514 1404 393
Answer:
7, 9, 11
Step-by-step explanation:
Let x represent the middle integer. Then the first is x-2, and the third is x+2. The given relation is ...
10(x -2) = 59 +(x +2)
10x -20 = x +61 . . . . eliminate parentheses
9x = 81 . . . . . . . . . . . add 20-x
x = 9 . . . . . . . . . . . . . divide by 9
The integers are 7, 9, 11.
_____
Check
7·10 = 11 +59 . . . true
find an equation for the plane that contains the line =(−1,1,2) (3,2,4) and is perpendicular to the plane 2 −3 4=0
Answers
The equation of the plane is:2x - 3y + 4z = 2.
Let's consider a line with the equation:(-1, 1, 2) + t(3, 0, -3), 0 ≤ t ≤ 1. The direction vector of this line is (3, 0, -3).
We must first find the normal vector to the plane that is perpendicular to the given plane.
The equation of the given plane is 2 - 3 + 4 = 0, which means the normal vector is (2, -3, 4).
As the required plane is perpendicular to the given plane, its normal vector must be parallel to the given plane's normal vector.
Therefore, the normal vector to the required plane is (2, -3, 4).
We will use the point (-1, 1,2) on the line to find the equation of the plane. Now, we have a point (-1, 1,2) and a normal vector (2, -3, 4).
The equation of the plane is given by the formula: ax + by + cz = d Where a, b, c are the components of the normal vector (2, -3, 4), and x, y, z are the coordinates of any point (x, y, z) on the plane.
Then we have,2x - 3y + 4z = d.
Now, we must find the value of d by plugging in the coordinates of the point (-1, 1,2).
2(-1) - 3(1) + 4(2) = d
-2 - 3 + 8 = d
d = 2
Therefore, the equation of the plane is:2x - 3y + 4z = 2
To know more about plane, visit:
brainly.com/question/12746252
#SPJ4
write standered form equation for the circle center (-7,4)

Answers
Answer:
Step-by-step explanation:
Gggg
calculators are sold to students for $20 each. 300 students are willing to buy them for that price. For each five dollars increase in price, there are 30 fewer students that are willing to buy the calculator.
a. what selling price will produce the maximum revenue?
b. what will the maximum revenue be?

Answers
Use mathematical induction to prove
2+7+12+17. +[5n-3]=n/2[5n-1]
Answers
By the principle of mathematical induction, the equation 2+7+12+17. +[5n-3]=n/2[5n-1] holds for all positive integers n.
To prove that the equation 2+7+12+17+...+[5n-3] = n/2[5n-1] holds for all positive integers n using mathematical induction, we need to show two things:
Base case: Prove that the equation holds for n=1.
Inductive step: Assume that the equation holds for n=k, and then show that it also holds for n=k+1.
Base case:
When n=1, we have:
2 = 1/2[5(1)-1]
2 = 1/2[4]
2 = 2
Therefore, the equation holds for n=1.
Inductive step:
Assume that the equation holds for n=k, i.e.,
2+7+12+17+...+[5k-3] = k/2[5k-1]
Now, we need to show that the equation also holds for n=k+1, i.e.,
2+7+12+17+...+[5(k+1)-3] = (k+1)/2[5(k+1)-1]
We can simplify the left-hand side of the equation as follows:
2+7+12+17+...+[5(k+1)-3] = [2+7+12+17+...+[5k-3]] + [5(k+1)-3]
Using the assumption from the inductive step, we can substitute k/2[5k-1] for the first part of the equation:
2+7+12+17+...+[5(k+1)-3] = k/2[5k-1] + [5(k+1)-3]
Simplifying the right-hand side of the equation:
2+7+12+17+...+[5(k+1)-3] = (5k² - k + 10k + 5) / 2
2+7+12+17+...+[5(k+1)-3] = (5k² + 9k + 5) / 2
2+7+12+17+...+[5(k+1)-3] = (k+1)/2[5(k+1)-1]
Therefore, the equation holds for n=k+1.
To learn more about proof click on,
https://brainly.com/question/31040447
#SPJ4
Tabo earns k4200 per month. His budget is k2500 for food, k300 for rent, k150 for clothes and k100 for other things. (a) how much does he spend each month ? ( b) how much does he have left to spend each month ?
Answers
Answer:
a) K3050 and b) K1150
Step-by-step explanation:
a) Add all his expenditures
i.e: K300+K150+K100
=K3050
b) Subtract the remaining of his spendings from the total
i.e: K4209 - K3050
=K1150
P
=
2
L
+
2
W
to find the length of a rectangle when the width is
4 1/2
inches and the perimeter is
29 2/5
inches.
Answers
Answer:
10 2/5 inches
Step-by-step explanation:
Since P=2L+2W, we can flip it to find the length. For example, we could minus 2L from both sides to get P-2L=2W.
We already know that W is 4.5, and P is 29.4.
Plugging that in, we get 29.4-2L=9. Again we can flip the perimeter, and -29.4 on both sides. This would make -2L=-20.4.
For our last flip, we divide the -2 from both sides to finally get L=10.2 (or 10 1/5 if you want) inches.
The function:
V(x) = x(10-2x)(16-2x), 0
a) Find the extreme values of V.
b) Interpret any valuse found in part (a) in terms of volumeof the box.
Answers
The minimum value of V occurs at x ≈ 0.93, which means that the volume of the box is smallest when the height is about 0.93 units.
To find the extreme values of V, we need to take the derivative of V and set it equal to zero. So, let's begin:
\(V(x) = x(10-2x)(16-2x)\)
Taking the derivative with respect to x:
\(V'(x) = 10x - 4x^2 - 32x + 12x^2 + 320 - 48x\)
Setting V'(x) = 0 and solving for x:
\(10x - 4x^2 - 32x + 12x^2 + 320 - 48x = 0\\8x^2 - 30x + 320 = 0\)
Solving for x using the quadratic formula:
\(x = (30 ± \sqrt{(30^2 - 4(8)(320))) / (2(8))\\x = (30 ± \sqrt{(1680)) / 16\\x = 0.93 or x =5.07\)
So, the extreme values of V occur at x ≈ 0.93 and x ≈ 5.07. To determine whether these are maximum or minimum values, we need to examine the second derivative of V. If the second derivative is positive, then the function has a minimum at that point. If the second derivative is negative, then the function has a maximum at that point. If the second derivative is zero, then we need to use a different method to determine whether it's a maximum or minimum.
Taking the second derivative of V:
V''(x) = 10 - 8x - 24x + 24x + 96
V''(x) = -8x + 106
Plugging in x = 0.93 and x = 5.07:
V''(0.93) ≈ 98.36 > 0, so V has a minimum at x ≈ 0.93.
V''(5.07) ≈ -56.56 < 0, so V has a maximum at x ≈ 5.07.
Now, to interpret these values in terms of the volume of the box, we need to remember that V(x) represents the volume of a box with length 2x, width 2x, and height x. So, the maximum value of V occurs at x ≈ 5.07, which means that the volume of the box is greatest when the height is about 5.07 units. The minimum value of V occurs at x ≈ 0.93, which means that the volume of the box is smallest when the height is about 0.93 units.
learn more about extreme values
https://brainly.com/question/1286349
#SPJ11
a) The extreme values of V are:
Minimum value: V(0) = 0
Relative maximum value: V(3) = 216
Absolute maximum value: V(4) = 128
b) The absolute maximum value of V at x = 4 represents the case where the box has a square base of side length 4 units, height 2 units, and width 8 units, which has a volume of 128 cubic units.
a) To find the extreme values of V, we first need to find the critical points of the function. This means we need to find where the derivative of the function equals zero or is undefined.
Taking the derivative of V(x), we get:
\(V'(x) = 48x - 36x^2 - 4x^3\)
Setting this equal to zero and solving for x, we get:
\(48x - 36x^2 - 4x^3 = 0\)
4x(4-x)(3-x) = 0
So the critical points are x = 0, x = 4, and x = 3.
We now need to test these critical points to see which ones correspond to maximum or minimum values of V.
We can use the second derivative test to do this. Taking the derivative of V'(x), we get:
\(V''(x) = 48 - 72x - 12x^2\)
Plugging in the critical points, we get:
V''(0) = 48 > 0 (so x = 0 corresponds to a minimum value of V)
V''(4) = -48 < 0 (so x = 4 corresponds to a maximum value of V)
V''(3) = 0 (so we need to do further testing to see what this critical point corresponds to)
To test the critical point x = 3, we can simply plug it into V(x) and compare it to the values at x = 0 and x = 4:
V(0) = 0
V(3) = 216
V(4) = 128
So x = 3 corresponds to a relative maximum value of V.
b) In terms of the volume of the box, the function V(x) represents the volume of a rectangular box with a square base of side length x and height (10-2x) and width (16-2x).
The minimum value of V at x = 0 represents the case where the box has no dimensions (i.e. it's a point), so the volume is zero.
The relative maximum value of V at x = 3 represents the case where the box is a cube with side length 3 units, which has a volume of 216 cubic units.
for such more question on extreme values
https://brainly.com/question/30886356
#SPJ11
Which expression is equivalent to 5 (3+4)?
A) 15 + 20
B) 15 + 4
© 8 + 9
D) 15 + 9
Answers
Answer:
15 + 20
Step-by-step explanation:
if it is correct then please mark as a brainlist
Answer:
A. 15+ 20
Step-by-step explanation:
5(3+4)
5(7)
=35
A. 15+20 = 35
35=35