If the side that is 6 units long is the base of this parallelogram, what is its corresponding height.
Answers
Answer:
4 units.
Step-by-step explanation:
No matter which side is chosen as the base, the area of the parallelogram is the product of that base and its corresponding height. With this we are trying to get 24 as area. So, since 6 units x 4 units = 24 units.
Thus, We can say the base is 6 units and height is 4 units.
Related Questions
Quadrilateral ABCD is transformed to create A'B'C'D'. Match the coordinates of A' with the transformations that create it
(2, 1)
(6, 12)
(2,4)
(4,-5)
(-2,4)
(2,-4)
(6.-12)
(-4,5)

Answers
The three basic types of rigid transformations are rotation, reflection and translation transformation
The correct options are;
Quadrilateral ABCD is reflected over the x-axis → (2, 4)
Quadrilateral ABCD translated 2 units right and 1 unit down → (4, -5)
Quadrilateral ABCD dilated about the origin by a scale factor of 3 → (6, -12)
Quadrilateral ABCD rotated 180° clockwise about the origin → (-2, 4)
The reasons the above matches are correct are as follows:
The given coordinates of the preimage are A(2, -4)
The image of (x, y) following a reflection over the x-axis is (x, -y)
Therefore
A(2, -4) in Quadrilateral ABCD is reflected over the x-axis → A'(2, 4)The image of (x, y) following a translation of 2 units right and 1 unit down → (x + 2, y - 1)
Therefore;
A(2, -4) in Quadrilateral ABCD translated 2 units right and 1 unit down → A'(4, -5)The image of (x, y) following a dilation about the origin by a scale factor of 3 is (3×x, 3×y)
Therefore;
A(2, -4) in Quadrilateral ABCD dilated about the origin by a scale factor of 3 → A'(6, -12)The image of the point (x, y) rotated 180° clockwise about the origin is (-x, -y)
Therefore;
A(2, -4) in Quadrilateral ABCD rotated 180° clockwise about the origin → A'(-2, 4)Learn more about rigid transformations here:
https://brainly.com/question/11018647
Answer:
look at the pic for correct answer
or my explanation below
Step-by-step explanation:
1....(2.4)
2...(4.-5)
3...(6.-12)
4...(-2.4)

in a class of 300 students, john's rank was 120. find his percentile rank.
Answers
John's percentile rank is 60%.
The percentile rank is a measure used to indicate the percentage of scores that fall below a particular value in a given data set. To calculate John's percentile rank, we first need to determine how many students are below his rank.
In this case, John's rank is 120, which means that 119 students are ranked higher than him, and 300 - 119 = 181 students are ranked lower than him. To find John's percentile rank, we divide the number of students ranked below him by the total number of students and multiply by 100: (181/300) x 100 = 60%.
Therefore, John's percentile rank is 60%, indicating that he scored higher than 60% of the students in his class.
For more questions like Number click the link below:
https://brainly.com/question/17429689
#SPJ11
a fruit stand has to decide what to charge for their produce. they need \$10$10dollar sign, 10 for 444 apples and 444 oranges. they also need \$12$12dollar sign, 12 for 666 apples and 666 oranges. we put this information into a system of linear equations. can we find a unique price for an apple and an orange?
Answers
No, we cannot find a unique price for an apple and an orange
Let the price of an apple be $x and that of orange be $y.
Condition 1.
They need $10 for 4 apples and 4 oranges.
Then, 4x + 4y = 10
or, 2x + 2y = 5 .....(1)
Condition 2.
They need $12 for 6 apples and 6 oranges.
Then, 6x + 6y = 12
or, 2x + 2y = 5 .....(2)
Two identical linear equations have been discovered.
They do, however, create a system of dependent linear equations that reduces to:
2x + 2y = 5
There are infinite possible solutions to this linear equation.
Thus, we get the conclusion that an apple and an orange cannot have different prices.
Learn more about linear equations:
https://brainly.com/question/13738061
#SPJ4
The slope (m) and the y-intercept (b) of the line 2x + 3y = 12 is:
Answers
Step-by-step explanation:
\(2x + 3y = 12 \\ 3y = - 2x + 12 \\ y = - \frac{2}{3} x + 4\)
slope is -2/3
y intercept is 4
Answer:
The slope is -2/3 and the y intercept is 4
Step-by-step explanation:
2x + 3y = 12
Slope intercept form of a line is
y = mx+b where m is the slope and b is the y intercept
2x + 3y = 12
Subtract 2x from each side
2x-2x+3y = -2x+12
3y = -2x+12
Divide by 3
3y/3 = -2x/3 +12/3
y = -2/3 x +4
The slope is -2/3 and the y intercept is 4
A new car is purchased for 24600 dollars. The value of the car depreciates at 13.75% per year. What will the value of the car be, to the nearest cent, after 15 years?
Answers
Answer:
The value will be $1,411.20
Step-by-step explanation:
What we do here is to set up an exponential equation to calculate the value.
Mathematically it will look like this;
V = I(1-r)^n
where V is the future value
I is the initial amount = 24,600
r is rate of decrease = 13.75% = 13.75/100 = 0.1375
n is the number of years = 15 years
substituting these values, we have
V = 24,600(1-0.1375)^15
V = 24600(0.8625)^15
V = 1,411.165582454129
= $1,411.20
¿Cuál es la suma de la medida de los ángulos interiores de un decágono?
Answers
Answer:
La suma de las medidas de los ángulos interiores de un decágono (polígono de 10 lados) es 1,440.
(8 points) Let a € R", where n ≥ 1 is an integer, and s, r € R with 0 < s < r. Define V = {x € R¹ : s < ||x − a|| < r}. Prove that V is open. ·
Answers
By showing for every point x in V, there exists an open ball B(x, ε) that is contained entirely within V we proved V is open.
To prove that V is open, we need to show that for every point x in V, there exists an open ball B(x, ε) that is contained entirely within V.
So take any point x in V. Since s < ||x − a|| < r,
we know that x is at a distance greater than s from a, but less than r.
Say this distance d = ||x − a||.
Now, Consider the point y that is halfway between x and a.
That is, let y = (x + a)/2.
Notice that ||x − y|| = ||a − y|| = d/2.
Since 0 < s < d/2, we know that s + d/2 < d.
Therefore, we can choose ε = d/2 − s such that B(x, ε) is contained entirely within set V.
To see this, let z be any point in B(x, ε). Then ||x − z|| < ε = d/2 − s,
which means that ||x − z|| + s < d/2.
But ||z − a|| ≤ ||x − a|| + ||x − z||, so we have,
⇒ ||z − a|| > ||x − a|| − ||x − z|| > d − (d/2 − s) = d/2 + s > s.
Therefore, z is in V, and since z was arbitrary,
we've shown that B(x, ε) is contained entirely within V.
Thus, we've shown that for every point x in V,
We can find an open ball B(x, ε) that is contained entirely within V. Therefore, V is open.
To learn more about open ball visit:
https://brainly.com/question/32835015
#SPJ4
Kiran mixes \frac{3}{4}
4
3
cups of raisins, 1 cup peanuts, and \frac{1}{2}
2
1
cups of chocolate chips to make trail mix. How much of each ingredient would he need to make 10 cups of trail mix? Explain your reasoning.
Answers
Step-by-step explanation:
7.5 cups of raisins, 10 cups of peanuts and 5 cups of chocolate chips.
Step-by-step explanation:
We are given that,
The amount of ingredients needed for the trail mix are,
Raisins = \frac{3}{4}
4
3
cup
Peanuts = 1 cup
Chocolate chips = \frac{1}{2}
2
1
cup
Since, Kiran needs to make 10 cups of the trail mix.
The amount of ingredients needed will be,
Raisins = \frac{3}{4}\times 10
4
3
×10 = \frac{30}{4}
4
30
= 7.5 cups
Peanuts = 1 × 10 = 10 cups
Chocolate chips = \frac{1}{2}\times 10
2
1
×10 = 5 cups
Hence, the ingredients needed are 7.5 cups of raisins, 10 cups of peanuts and 5 cups of chocolate chips.
4 1/4 not sure tho i got it from internet
a professor packs her collection of 40 issues of a mathe- matics journal in four boxes with 10 issues per box. how many ways can she distribute the journals if a) each box is numbered, so that they are distinguish- able?
Answers
If each box is numbered , so that they are distinguishable , then professor can distribute the journal in 40!/(10! )⁴ ways .
In the question ,
it is given that
the professor had 40 issues of mathematics journal;
number of boxes to be packed in = 4 boxes
number of issues per box = 10 issues
since the 4 boxes are numbered ,
So , in
Box 1 , the 10 issues out of 40 can be packed in ⁴⁰C₁₀ ways .
and
for box 2 the number of issues remaining is 30
So , in Box 2 the 10 issues out of 30 can be packed in ³⁰C₁₀ ways .
for Box 3
the number of issues remaining is 20
so, in box 3 the 10 issues out of 20 can be filled in ²⁰C₁₀ ways .
for Box4
the umber of issues remaining is 10 ,
so , in box 4 the 10 issues out of 10 can be filled in ¹⁰C₁₀ ways .
The journals can be distributed in ⁴⁰C₁₀ × ³⁰C₁₀ × ²⁰C₁₀ × ¹⁰C₁₀ ways
= (40!)/(30! * 10! ) × (30!)/( 20! * 10!) × (20!)/(10! * 10!) × 1
On simplifying further , we get
= 40!/(10! )⁴ ways .
Therefore , If each box is numbered , so that they are distinguishable , then professor can distribute the journal in 40!/(10! )⁴ ways .
Learn more about Combination here
https://brainly.com/question/13676779
#SPJ4
help with this problem

Answers
the paragraph includes exaggeration. trees are not able to actually gather around and the rivers won’t be able to stop flowing.
hope this helps!
is the coefficient for household income growth statistically significant?yes it is statistically significant at 5% level.yes it is statistically significant at 1% level.no it is statistically insignificant.yes it is statistically significant at 0.73% level.
Answers
The coefficient for household income growth is statistically significant at the 5% level.
To determine the statistical significance of the coefficient for household income growth, a significance level or alpha is needed. The significance level indicates the threshold below which the coefficient is considered statistically significant.
The given statement states that the coefficient is statistically significant at the 5% level. This means that the probability of observing such a large coefficient due to random chance is less than 5%. In other words, there is strong evidence to suggest that the coefficient is not zero and that there is a significant relationship between household income growth and the variable of interest.
It is important to note that the other options stating significance at the 1% level or 0.73% level would indicate even stronger evidence against the null hypothesis.
Learn more about statistical significance here:
https://brainly.com/question/30311816
#SPJ11
witch one is the function

Answers
Answer:
B
Step-by-step explanation:
a function doesn't have any repeating x values
2. An organization has 20 male and 18 female members. In how many ways can five male and five female members be selected to sit on the board of directors? Explain your solution (12)
Answers
To determine the number of ways to select five male and five female members for the organization's board of directors, we'll use the combination formula C(n, r) = n! / (r! * (n-r)!). So, there are 132,819,072 ways to select five male and five female members for the organization's board of directors.
For the male members, n = 20 and r = 5. So, we'll calculate C(20, 5):C(20, 5) = 20! / (5! * (20-5)!)
C(20, 5) = 20! / (5! * 15!)
C(20, 5) = 15,504
For the female members, n = 18 and r = 5. So, we'll calculate C(18, 5):C(18, 5) = 18! / (5! * (18-5)!)C(18, 5) = 18! / (5! * 13!)C(18, 5) = 8,568Now, we'll multiply the number of ways to choose male and female members to get the total number of ways to form the board of directors:Total ways = 15,504 (male) * 8,568 (female)Total ways = 132,819,072know more about combination formula here: https://brainly.com/question/28065038
#SPJ11
[r] bastien, inc. has been manufacturing small automobiles that have averaged 45 miles per gallon of gasoline in highway driving. the company has developed a more efficient engine for its small cars and now advertises that its new small cars average more than 45 miles per gallon in highway driving. an independent testing service road-tested 52 of the automobiles. the sample showed an average of 46.1 miles per gallon. the sample standard deviation is 5.3 miles per gallon. conduct an appropriate hypothesis test. find the t-statistic and the appropriate conclusion at the 0.01 level of significance.
Answers
According to the hypothesis test we find out that the t-statistic is 0.634 and thus, conclude that the manufacturer's advertising campaign is incorrect as its new small cars have an average of less than or equal to 45 miles per gallon in highway driving.
It is given to us that -
Company manufactures small automobiles that have averaged 45 miles per gallon of gasoline in highway driving
Company now advertises that its new small cars average more than 45 miles per gallon in highway driving
52 automobiles were tested
Sample average is 46.1 miles per gallon
Sample standard deviation is 5.3 miles per gallon
Significance level is 0.01
We have to conduct an appropriate hypothesis test and find the t-statistic and determine the correct conclusion.
Let us assume that -
p = population of average gasoline of new small cars in highway driving
According to the given information,
Null hypothesis represents that the advertising campaign of the manufacturer is incorrect. This implies that -
\(H_{0}\) : \(p\leq 45\) miles per gallon
Alternative hypothesis represents that the advertising campaign of the manufacturer is correct. This implies that -
\(H_{A}\) : \(p > 45\) miles per gallon
For carrying out the hypothesis test for the given situation we have to apply one sample z test statistic since the sample standard deviation information is available to us.
According to one sample z test, the value of test statistic is given as -
\(T = \frac{(X_{avg} -p)}{\frac{S}{\sqrt{n} } }\) ------ (1)
where,
\(X_{avg}\) = Sample mean
p = hypothesized population mean
S = Sample standard deviation
n = Sample size
According to the given information, we have
\(X_{avg}\) = 46.1 miles per gallon
p = 45 miles per gallon
S = 5.3 miles per gallon
n = 52
Substituting the above values in equation (1), we have
\(T = \frac{(X_{avg} -p)}{\frac{S}{\sqrt{n} } }\\= > T = \frac{(46.1 -45)}{\frac{5.3}{\sqrt{52} } }\\= > T = \frac{1.1}{0.735}\\ = > T = 0.634\)
It is given to us that the significance level is 0.01. According to the z-table, the critical value of the test statistic at 0.01 significance level is 2.58.
But, we see that the test statistic that we obtained above is less than the critical value at significance level of 0.01. i.e.,
0.634 < 2.58
This implies that there is not sufficient evidence for us to reject the null hypothesis for this particular situation.
Therefore, we can conclude from the hypothesis test that the t-statistic is 0.634 and thus, the manufacturer's advertising campaign is incorrect as its new small cars have an average of less than or equal to 45 miles per gallon in highway driving.
To learn more about hypothesis test visit https://brainly.com/question/17347077
#SPJ4
According to the hypothesis test we find out that the t-statistic is 0.634 and thus, conclude that the manufacturer's advertising campaign is incorrect as its new small cars have an average of less than or equal to 45 miles per gallon in highway driving.
It is given to us that -
Company manufactures small automobiles that have averaged 45 miles per gallon of gasoline in highway driving
Company now advertises that its new small cars average more than 45 miles per gallon in highway driving
52 automobiles were tested
Sample average is 46.1 miles per gallon
Sample standard deviation is 5.3 miles per gallon
Significance level is 0.01
We have to conduct an appropriate hypothesis test and find the t-statistic and determine the correct conclusion.
Let us assume that -
p = population of average gasoline of new small cars in highway driving
According to the given information,
Null hypothesis represents that the advertising campaign of the manufacturer is incorrect. This implies that -
H0 = p<= 45 : miles per gallon
Alternative hypothesis represents that the advertising campaign of the manufacturer is correct. This implies that -
HA : p > 45 : miles per gallon
For carrying out the hypothesis test for the given situation we have to apply one sample z test statistic since the sample standard deviation information is available to us.
According to one sample z test, the value of test statistic is given as -
T = (X - p)/(SD/√n)
where,
X = Sample mean
p = hypothesized population mean
S = Sample standard deviation
n = Sample size
According to the given information, we have
X = 46.1 miles per gallon
p = 45 miles per gallon
S = 5.3 miles per gallon
n = 52
Substituting the above values in equation (1), we have
T = 46.1-45/(5.2/√52)
T = 1.1/0.735
T = 0.634
It is given to us that the significance level is 0.01. According to the z-table, the critical value of the test statistic at 0.01 significance level is 2.58.
But, we see that the test statistic that we obtained above is less than the critical value at significance level of 0.01. i.e.,
0.634 < 2.58
This implies that there is not sufficient evidence for us to reject the null hypothesis for this particular situation.
Therefore, we can conclude from the hypothesis test that the t-statistic is 0.634 and thus, the manufacturer's advertising campaign is incorrect as its new small cars have an average of less than or equal to 45 miles per gallon in highway driving.
To learn more about hypothesis test visit brainly.com/question/17347077
#SPJ4
Seven subtracted from a number is -18
Answers
Answer:
-11
Step-by-step explanation:
Just add 7 to -18
-18 + 7 = -11
Hope this helped :)
(If you want to check, just do -11 - 7)
Select the correct answer.
The perimeter of a rectangle is 42 inches. If the width of the rectangle is 6 inches, what is the length?
Answers
Answer:
7 inches
Step-by-step explanation:
6x7=
42
Determine if the sequence below is arithmetic or geometric and determine the common difference/ratio in the simplest form 2,8,32,…
I need this filled out in this format;
This is a____ sequence and the common ratio/common difference(choose one) is equal to___
Answers
Notice:
2 is first term
2*4 = 8 is second term
8*4 = 32 is third term
and so on
Each term is multiplied by 4 to get the next term, so it’s geometric. The “common ratio” is whatever you’re multiplying by, which is 4.
You need 50, 4ounce portions of green beans. Fresh green beans yield 85% edible product after they have been cleaned and trimmed. How many pounds of fresh green beans do you need to purchase? 2. You need ten pounds of fish for stew. The whole fish you are purchasing has a 40% yield after it has been cleaned. How much whole fish do you need to purchase? 3. You are serving a half-pound strip sirloin for a special. Your forecast projects that 60 people will order sirloin, so how many pounds of sirloin should you bring in if, after trimming, you usually have 20% waste?
Answers
1. To have 50, 4-ounce portions of green beans, we need to find how many pounds of fresh green beans should be bought.
Firstly, we'll need to find out how many ounces are needed to have a total of 50 portions of 4-ounces each.
50 portions of 4 ounces each = 50 × 4 = 200 ounces.
To find the total weight in ounces of the green beans that need to be purchased, we divide 200 by 0.85 (as 85% of fresh green beans are edible) as follows:
Total weight in ounces = 200/0.85 = 235.29 ounces.
1 pound is equal to 16 ounces, so to find the total weight in pounds of fresh green beans, we divide 235.29 by 16 as follows:
Total weight in pounds = 235.29/16 = 14.7 pounds.
Therefore, approximately 15 pounds of fresh green beans should be purchased.
2. We need to find out how much whole fish we need to buy to obtain 10 pounds of fish after it has been cleaned (with 40% yield).
We can solve for this using the formula: Yield% = (edible portion ÷ raw portion) × 100.
We can rearrange the formula as: Edible portion = (yield% ÷ 100) × raw portion
We need a 40% yield, so substituting the given values in the formula above, we get:
Edible portion = (40 ÷ 100) × Raw portion
Let's say Raw portion is R. We need 10 pounds of edible portion, so:
10 pounds = (40 ÷ 100) × R10 ÷ (40 ÷ 100) = R25 = R
Therefore, 25 pounds of whole fish should be purchased.
3. We are serving 60 people with half-pound strip sirloin, so we need to find how many pounds of sirloin should be brought in, assuming that 20% of it will be wasted after trimming.
Each serving requires a half-pound, so 60 people need a total of 60 × 0.5 = 30 pounds of sirloin.
To find out the total weight of sirloin that should be brought in, we can use the formula:
Total weight of sirloin = Required weight of sirloin ÷ (1 - Waste%)
Required weight of sirloin = 30 pounds
Waste% = 20% = 0.2
Substituting these values into the formula, we get:
Total weight of sirloin = 30 ÷ (1 - 0.2)= 30 ÷ 0.8= 37.5 pounds.
So, approximately 38 pounds of sirloin should be brought in.
Learn more about purchasing at
https://brainly.com/question/24112214
#SPJ11
The function f(x) = -2-^3 + 5x^2 - 3x + 1 is
A. Neither even or odd
B. Odd
C. Even
D. Symmetric about the y-axis
Answers
Analyzing the function f(x) = -2•x³ + 5•x² - 3•x + 1, using the criteria f(x) = f(-x) for even functions and f(x) = -f(-x) for odd functions, gives the correct option as the option
A. Neither even or odd
What are the the differences between even and odd functions?An even function satisfy the equation f(x) = f(-x)
An even function is one that is symmetrical about the y-axis
An odd function satisfy the equation f(x) = -f(-x)
The shape graph of an odd function is inverted as it crosses the y-axis.
Analyzing the function f(x) = -2•x³ + 5•x² - 3•x + 1 gives;
f(1) = -2•1³ + 5•1² - 3•1 + 1 = -1
f(-1) = -2•(-1)³ + 5•(-1)² - 3•(-1) + 1 = 11
f(1) ≠ f(-1)
-f(-1) = -2•(-1)³ + 5•(-1)² - 3•(-1) + 1 = 11
f(1) ≠ -f(-1)
The function is therefore;
A. Neither even or oddLearn more about the graphs of functions here:
https://brainly.com/question/17089414
#SPJ1
Find the standard form.
500,000 + 30,000 + 5,000 + 300 + 50 + 3
A) 535,535
B) 535,353
C) 535,000
Answers
Answer:
B.
Step-by-step explanation:
Lets break this down piece by piece.
So first, add 500,000 and 30,000. that would be 530,000.
Next, add on 5,000, which is 535,000
After that, add 300. ( 535,300. )
Then add up 50 and 3 which is 53.
Lastly, your answer is 535,353.
Answer:
b
Step-by-step explanation:b
b
Which method can you use to prove that the triangles are congruent

Answers
Answer:
HL
Step-by-step explanation:
It's a right triangle.
Answer: HL
Step-by-step explanation: because they are right triangles
a student of 9 engines contains 2 defective engines. an auto shop buys 4 engineers. what is the probability of the shop purchasing at least 3 non-defective engines?
Answers
The probability of the shop purchasing is 5/9.
How to find probability shop purchasing?Let X be the number of non-defective engines purchased by the auto shop out of the 4 engines bought. We want to find P(X >= 3), the probability of getting at least 3 non-defective engines.
Using the hypergeometric distribution formula, we have:
P(X >= 3) = P(X = 3) + P(X = 4)
where
P(X = k) = (C(7, k) * C(2, 4-k)) / C(9, 4)
So, we have:
P(X = 3) = (C(7, 3) * C(2, 1)) / C(9, 4) = (35 * 2) / 126 = 5/18
P(X = 4) = (C(7, 4) * C(2, 0)) / C(9, 4) = (35 * 1) / 126 = 5/18
Therefore,
P(X >= 3) = 5/18 + 5/18 = 10/18 = 5/9
So the probability of the shop purchasing at least 3 non-defective engines is 5/9.
Learn more about probability
brainly.com/question/30034780
#SPJ11
a manufacturer knows that their items have a normally distributed lifespan, with a mean of 3.1 years, and standard deviation of 0.5 years. the 10% of items with the shortest lifespan will last less than how many years? give your answer to one decimal place.
Answers
The shortest lifespan will last less than 2.5 years.
What is standard deviation?
The standard deviation is a statistic that expresses how much variance or dispersion there is in a group of numbers. While a high standard deviation suggests that the values are dispersed throughout a wider range, a low standard deviation suggests that the values tend to be close to the established mean.
First, we must utilize the conventional normal table to determine the value for z if 10% of the region (probability) to its left will be present. We can observe that about z = -1.282.
Now, we have to find the value of x, that corresponds to the value of z.
Since,
(x - μ) / σ = z
(x - 3.1) / 0.5 = -1.282
x = 2.459
Hence, the shortest lifespan will last less than 2.5 years.
To know more about the standard deviation, click on the link
https://brainly.com/question/475676
#SPJ4
find the measure of the missing angle (#4 btw)

Answers
Answer:
Step-by-step explanation:
1)
∠1 = ∠2 {Angles opposite to equal angles are equal}
∠1 = ∠2 = x
x +x + 55 = 180 {angle sum property of triangle}
2x + 55 = 180
2x = 180 - 55
2x = 125
x = 125/2
x = 62.5
∠1 = 62.5
2) ∠2 = 62.5
3) ∠3 = 55 {Vertically opposite angles are congruent}
4) ∠4 + 105 = 180 {linear pair}
∠4 = 180 - 105
∠4 = 75
5) ∠3 + ∠4 + ∠5 = 180 {Angle sum property of triangle}
55 + 75 +∠5 = 180
130 + ∠5 = 180
∠5 = 180 - 130
∠5 = 50
write a equation to find the "n" term of each sequence
1,3,5,7,....
Answers
Answer:
a1=1
d=3-1
=2
an=a1+(n-1)d
=1+ (n-1)2
=1+2n-2
2n-1
does the higher cost of tuition translate into higher-paying jobs? the table lists the top ten colleges based on mid-career salary and the associated yearly tuition costs. construct a scatter plot of the data. school mid-career salary (in thousands) yearly tuition princeton 137 28,540 harvey mudd 135 40,133 caltech 127 39,900 us naval academy 122 0 west point 120 0 mit 118 42,050 lehigh university 118 43,220 nyu-poly 117 39,565 babson college 117 40,400 stanford 114 54,506 webassign plot webassign plot webassign plot webassign plot
Answers
The “yearly tuition costs” as an independent variable which should be plotted on X-axis and “mid-career salary” as a dependent variable on Y-axis. The scatterplot is made of them.
Based on the table provided, it is possible to observe that there is not necessarily a clear relationship between the cost of tuition and mid-career salary.
While some of the colleges with higher tuition costs (such as MIT and Stanford) have high mid-career salaries, others (such as Harvey Mudd and Caltech) also have high mid-career salaries despite lower tuition costs. Additionally, some colleges with low or zero tuition costs (such as the US Naval Academy and West Point) also have high mid-career salaries.
Therefore, it is not safe to assume that a higher cost of tuition will necessarily translate into higher-paying jobs. The scatter plot of yearly tuition costs and mid-career salary is made.
To know more about Scatter plot:
https://brainly.com/question/29231735
#SPJ4


Solve the equation for the variable:
1.) x^2 - 12x = 45
2.) x^2 - 6x = 7
Answers
Answer:
Given Below.
Explanation:
(a)
\(x^2 - 12x = 45\)
\(x^2 - 12x -45 = 0\)
\(x^2 - 15x + 3x - 45 = 0\)
\(x ( x-15) + 3 ( x - 15) = 0\)
\((x+3)(x-15) = 0\)
\(x = -3 , 15\)
(b)
\(x^2 - 6x = 7\)
\(x^2 - 6x -7 = 0\)
\(x^2-7x + x -7 = 0\)
\(x(x-7)+1(x-7) = 0\)
\((x+1)(x-7) =0\)
\(x = -1, 7\)
1. )
\(x^{2} -12x=45\\x^{2} -12x-45 = 0\\(x-15)(x+3) = 0\\x = -3, 15\)
2. )
\(x^{2}-6x=7\\x^{2} -6x-7=0\\(x-7)(x+1) = 0\\x = -1, 7\)
What two numbers have a product of -57 and a sum of -16?
Answers
Answer:
-19 and 3
Step-by-step explanation:
-19 x 3 = -57
-19 + 3 = -16
Answer:
Step-by-step explanation: To find the answer to "What two numbers have a product of 57 and a sum of 16?" we first state what we know. We are looking for x and y and we know that x • y = 57 and x + y = 16.
Before we keep going, it is important to know that x • y is the same as y • x and x + y is the same as y + x. The two variables are interchangeable. Which This means that when we create one equation to solve the problem, we will have two answers.
To solve the problem, we take x + y = 16 and solve it for y to get y = 16 - x. Then, we replace y in x • y = 57 with 16 - x to get this:
x • (16 - x) = 57
Like we said above, the x and y are interchangeable, therefore the x in the equation above could also be y. The bottom line is that when we solved the equation we got two answers which are the two numbers that have a product of 57 and a sum of 16. The numbers are:
5.35425
10.64575
That's it! The two numbers that have a product of 57 and a sum of 16 are 5.35425 and 10.64575 as proven below:
5.35425 • 10.64575 = 57
5.35425 + 10.64575 = 16
HOPE THAT HELP YOU PLS MARK ME BRANLITS PLSSSS
help with simplifying
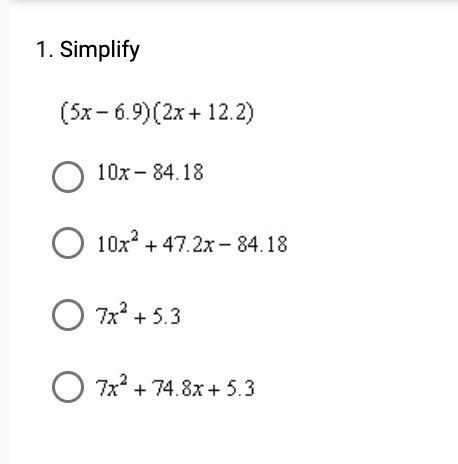
Answers
Option B: \(10x^2 + 47.62x - 84.18.\) is correct
What is the quadratic equation?
A quadratic equation is an equation of the form ax^2 + bx + c = 0, where a, b, and c are constants and x is the variable being solved for.
The values of x that satisfy the equation are called solutions of the equation, and roots or zeros of the expression on its left-hand side. A quadratic equation has at most two solutions.
If there is only one solution, one says that it is a double root. If all the coefficients are real numbers, there are either two real solutions, or a single real double root, or two complex solutions that are complex conjugates of each other.
To simplify the expression, we need to use the distributive property of multiplication.
\((5x - 6.9)(2x + 12.2)\\= 5x(2x) + 5x(12.2) - 6.9(2x) - 6.9(12.2)\\= 10x^2 + 61x - 13.38x - 84.18\\= 10x^2 + 47.62x - 84.18\\\)
Hence, (5x - 6.9)(2x + 12.2) simplifies to \(10x^2 + 47.62x - 84.18\).
To learn more about quadratic equation, Visit
https://brainly.com/question/1214333
#SPJ1
As an estimation we are told 5 miles is 8 km.
Convert 2.5 miles to km.
Answers
Answer:
\(4km\)
Step-by-step explanation:
In order to find the answer to this question you must simply divide.
\(5m=8km\)
\(2.5m=4km\)
\(8\div2=4\)
\(5=2.5+2.5\)
\(=4km\)
Hope this helps