if f of x equals x +9 and g of x equals -6 which describes the range of f +g times x
Answers
The range of (f+g)(x) is all real numbers.
To find the range of (f+g)(x), where f(x) = x+9 and g(x) = -6, follow these steps:
1. Combine f(x) and g(x) using the sum function: (f+g)(x) = f(x) + g(x)
2. Substitute the functions into the equation: (f+g)(x) = (x+9) + (-6)
3. Simplify the equation: (f+g)(x) = x+3
Now that we have (f+g)(x) = x+3, we can determine the range.
Since x can be any real number, the range of (f+g)(x) is also all real numbers because adding 3 to any real number still results in a real number.
Therefore, the range of (f+g)(x) is all real numbers.
Know more about the range here:
https://brainly.com/question/2264373
#SPJ11
Related Questions
a ______ is a descriptiion of the approach that is used to obtain samples from a population prior to an data collection activity.
A.
population frame
B.
sampling weight
C.
sampling plan
D.
probability interval
Answers
The correct answer is option C. A sampling plan refers to a detailed strategy for obtaining a sample from a population for the purpose of data collection.
It describes the precise procedures needed to choose the sample, determine the members of the sample, and gather the data.
The sampling strategy should take into account the type of sampling design, sample size, sampling process, and the methods to be employed for data collecting.
The strategy for implementing sampling should be outlined in the plan, along with instructions on how to make sure the sample is representative of the population, how to prevent bias in the sampling process, and how to make sure the data gathered is of high quality.
A good sampling plan should provide a clear and consistent method for gathering data and be founded on basic statistical concepts.
To learn more about sampling plan visit:
https://brainly.com/question/18026723
#SPJ4
Robert bought 2.45 pounds of trail mix. The trail mix costs $6.75 per pound.
How much did Robert spend for the trail mix?
Answers
Answer:
Robert spent $16.5375 for the trail mix.
Explanation:
1 pounds ⇒ $6.75
2.45 pounds ⇒ ( $6.75 * 2.45 ) = $16.5375
Total cost:-
2.45(6.75)16.54$What is the radius and diameter of the following circle?

Answers
Answer:
Radius = 16cm
Diameter = 32cm
Step-by-step explanation:
The Radius of a circle is half the diameter of the circle. The radius is how far the outside of the circle is from the middle of the circle. To find the Diameter add the radius twice, for example 16+16. Don’t forget your UNIT it is in Centimeters in this case.
The radius is 16
Diamiter is 32
the roman numeral lvii represents which of these numbers?
Answers
L = 50
X = 10
I = 1
Roman numbers are written from left to right with the largest number first. If a smaller number is written before a larger number, it is subtracted from the larger number. So here we have 50 less 10 which gives us 40. The II gives us the number 2, which we add to the 40 as each I follows the larger number.
hope this helps!
In Exercises 18-21, use Exercise 14 and property 2 of Theorem 5 to test for linear independence in P_3. 21. {x^3 +1, x^2 +1, x + 1,1} 14. Prove that (1, x,x^2,...,x^n) is a linearly indepen- dent set in P^n by supposing that p(x) = θ(x), where p(x) = a_0+ax_1...+a_n x^n. Next, take successive derivatives as in Example 2. 2. The set Sis linearly independent in V if and only if the set T is linearly inde- pendent in RP.
Answers
\((x^3 + 1, x^2 + 1, x + 1, 1)\) is also linearly independent in higher-degree spaces such as \(P^4, P^5\), and so on.
To test for linear independence in the vector space of polynomials of degree at most 3, denoted as \(P_3\), we can use Exercise 14 and Property 2 of Theorem 5.
Exercise 14 states that if the vectors in the set \((1, x, x^2, ..., x^n)\) are linearly independent in \(P^n\), then the set is linearly independent in \(P^{n+1}\).
Property 2 of Theorem 5 states that if a set S = \((v_1, v_2, ..., v_n)\) is linearly independent and the vector v is such that v does not belong to the subspace spanned by S, then the set \((v_1, v_2, ..., v_n, v)\) is also linearly independent.
Now, let's apply these concepts to Exercise 21, where we have the set \((x^3 + 1, x^2 + 1, x + 1, 1)\).
Suppose we have a polynomial p(x) = \(a_0 + a_1x + a_2x^2 + a_3x^3\), such that p(x) = 0 for all x.
If p(x) = 0, then \(a_0 + a_1x + a_2x^2 + a_3x^3\) = 0 for all x.
Taking x = 0, we get \(a_0 = 0\).
Taking x = 1, we get \(a_0 + a_1 + a_2 + a_3 = 0\).
Taking x = -1, we get \(a_0 - a_1 + a_2 - a_3 = 0\).
Taking x = 2, we get \(a_0 + 2a_1 + 4a_2 + 8a_3 = 0\).
From the first equation, we have \(a_0 = 0\). Substituting this into the second and third equations, we get:
\(0 + a_1 + a_2 + a_3 = 0\),
\(0 - a_1 + a_2 - a_3 = 0\).
Adding the second and third equations, we obtain:
\(2(a_2 + a_3) = 0\).
Since this equation must hold for all x, it implies that \(a_2 + a_3 = 0\). Therefore, \(a_2 + a_3 = 0\).
Substituting this back into the second equation, we have:
\(a_1 + (-a_3) + a_3 = 0,\\a_1 = 0.\)
We now have \(a_0 = a_1 = 0\). Substituting these values into the fourth equation, we get:
\(0 + 2a_1 + 4a_2 + 8a_3 = 0,\\0 + 4a_2 + 8a_3 = 0,\\2a_2 + 4a_3 = 0,\\2(a_2 + 2a_3) = 0.\).
This implies that \(a_2 + 2a_3 = 0\), and since \(a_2 = -a_3\), we have:
\(-a_3 + 2a_3 = 0,\\a_3 = 0.\)
Therefore, all the coefficients \(a_0, a_1, a_2, and a_3\) are zero. This shows that the set \((x^3 + 1, x^2 + 1, x + 1, 1)\) is linearly independent in P_3.
By Exercise 14 and Property 2, we can conclude that \((x^3 + 1, x^2 + 1, x + 1, 1)\) is also linearly independent in higher-degree spaces such as P^4, P^5, and so on.
Learn more about linear independence:
brainly.com/question/29740341
#SPJ4
Select all the names of figures that could
also be classified as a rhombus.
(a) parallelogram
(b) square
lot
(c) rectangle
(d) quadrilateral
(e) triangle
no
Answers
The figures that could also be classified as a rhombus are:
(b) square
(c) rectangle
A rhombus is a quadrilateral with all sides congruent, so any figure that has this property can also be classified as a rhombus. A square is a special type of rhombus where all angles are right angles, while a rectangle is a parallelogram with all angles at 90 degrees. Therefore, both a square and a rectangle have all sides congruent, making them also rhombuses. A parallelogram and a quadrilateral may or may not have congruent sides, so they cannot be classified as rhombuses. A triangle is a three-sided polygon, so it cannot be classified as a rhombus either.
Learn more about rhombus here: brainly.com/question/16425804
#SPJ11
The names of figures that could also be classified as a rhombus are:
(b) Square
(d) Quadrilateral
A rhombus is a type of quadrilateral with four equal sides. A square is also a type of quadrilateral with four equal sides, so it can also be classified as a rhombus. However, not all quadrilaterals are rhombuses. For example, a rectangle is a type of quadrilateral with two pairs of equal sides, but its angles are not all equal, so it is not a rhombus. It's worth noting that while all squares are rhombuses, not all rhombuses are squares. A square is a special type of rhombus where all angles are right angles.
Learn more about quadrilateral here: brainly.com/question/19338711
#SPJ11
Find the measure of one of the interior angles of a
regular polygon with 8 sides.
A
1080°
B
157.5°
с
135°
D
202.5°
Help plss
Answers
A 5 kg box is sliding up a 10 degree ramp at 5 m/s. If the frictional coefficient between the box and the ramp is 0.2, how far will the box slide?
Answers
the box will slide approximately 12.56 meters up the ramp.
To determine how far the box will slide up the ramp, we need to consider the forces acting on the box.
Given:
Mass of the box (m) = 5 kg
Initial velocity of the box (v) = 5 m/s
Angle of the ramp (θ) = 10 degrees
Frictional coefficient (μ) = 0.2
We can break down the forces acting on the box into components parallel and perpendicular to the ramp:
1. Force parallel to the ramp (F_parallel):
F_parallel = m * g * sin(θ)
where g is the acceleration due to gravity (9.8 m/s^2).
2. Force perpendicular to the ramp (F_perpendicular):
F_perpendicular = m * g * cos(θ)
Next, we calculate the frictional force (F_friction):
F_friction = μ * F_perpendicular
Since the box is sliding up the ramp, the net force acting on the box in the direction of motion is given by:
Net force = F_parallel - F_friction
Using Newton's second law of motion, we have:
Net force = m * acceleration
Solving for the acceleration:
acceleration = Net force / m
Since the box is sliding up the ramp, the acceleration is negative.
Using the equations above, we can calculate the acceleration of the box.
F_parallel = 5 kg * 9.8 m/s² * sin(10 degrees) ≈ 8.504 N
F_perpendicular = 5 kg * 9.8 m/s² * cos(10 degrees) ≈ 47.489 N
F_friction = 0.2 * 47.489 N ≈ 9.498 N
Net force = 8.504 N - 9.498 N ≈ -0.994 N
acceleration = (-0.994 N) / 5 kg ≈ -0.199 m/s²
Next, we can use the kinematic equation to determine the distance the box will slide up the ramp:
v² = u² + 2as
Since the box is starting from rest (u = 0), the equation simplifies to:
v² = 2as
Solving for s (distance):
s = (v²) / (2 * |acceleration|)
s = (5 m/s)² / (2 * 0.199 m/s²) ≈ 12.56 m
Therefore, the box will slide approximately 12.56 meters up the ramp.
Learn more about forces here
https://brainly.com/question/30507236
#SPJ4
a binary tree is a structure in which each node is capable of having successor nodes, called .
Answers
A binary tree is a structure in which each node is capable of having two successor nodes, called "left child" and "right child."
In a binary tree, each node can have at most two successor nodes, known as the left child and the right child. These successor nodes branch out from the parent node, forming two distinct paths or branches. The left child represents the left branch, and the right child represents the right branch. This hierarchical structure allows for efficient organization and traversal of data, as each node can connect to two other nodes, creating a branching pattern throughout the tree. The concept of left and right children enables various operations and algorithms to be performed on the binary tree, such as insertion, deletion, searching, and sorting.
To know more about binary tree,
https://brainly.com/question/33461694
#SPJ11
An ice field is melting at a rate of M(t)=4-sin^3 t acre-feet per day. How many acre feet of this ice field will melt from the beginning of day 1 (t=0) to the beginning of day 4 (t=3).
Answers
the amount of ice that will melt from the beginning of day 1 to the beginning of day 4 can be found by integrating the rate of melting over that time period.
To find the amount of ice that melts over the time period from t=0 to t=3, we need to integrate the given rate of melting function, M(t)=4-sin^3 t, over that time period. Using the fundamental theorem of calculus, we can find the antiderivative of M(t):
∫M(t)dt = ∫(4-sin^3 t)dt = 4t + (3/4)cos(t) + (1/12)cos^3(t)
Evaluating this antiderivative from t=0 to t=3, we get:
(4(3) + (3/4)cos(3) + (1/12)cos^3(3)) - (4(0) + (3/4)cos(0) + (1/12)cos^3(0))
Simplifying this expression, we get:
12 + (3/4)cos(3) + (1/12)cos^3(3) - (3/4)
Therefore, the amount of ice that will melt from the beginning of day 1 to the beginning of day 4 is approximately 11.56 acre-feet.
we can find the amount of ice that will melt over a given time period by integrating the rate of melting function over that time period. In this case, we found that approximately 11.56 acre-feet of the ice field will melt from the beginning of day 1 to the beginning of day 4.
To know more about time period, visit:
https://brainly.com/question/31824035
#SPJ11
In the first event, the eighth graders are running a baton relay race with three other classmates. The teams top speed for each leg is 56.8 one seconds, 59.22 seconds, 57.39 seconds, and 60.11 seconds. Use the information to protect his teams best time for the race. Each leg of the race from part a is the same distance. Calculate the teams average time for each leg of the race. Show your work
Answers
Answer:
The best time is 56.81 seconds
Average leg time is 58.3825 seconds
Step-by-step explanation:
Here, we want to start by stating the team’s best time for the race
The team’s best time for the race is the smallest time spent on a lap
From the times given, the best time is 56.81 seconds
Now, we want to calculate the average time
We simply add up all these and divide by count
Mathematically, that will be;
(56.81 + 59.22 + 57.39 + 60.11)/4 = 58.3825 seconds
can so.eone explain to me by what bisecting intervals are?

Answers
When you bisect something, you cut it into two equally sized pieces. (from Latin: "bi" = two, "sect" = cut)
Bisecting an interval creates two smaller intervals each with half the length of the original interval. Some examples:
• bisecting [0, 2] gives the intervals [0, 1] and [1, 2]
• bisecting [-1, 1] gives the intervals [-1, 0] and [0, 1]
• bisecting an arbitrary interval \([a,b]\) gives the intervals \(\left[a,\frac{a+b}2\right]\) and \(\left[\frac{a+b}2,b\right]\)
how many 1/2 cup serving would 3 gallons of punch provide?
Answers
Answer: 96 servings.
Step-by-step explanation:
There are 16 cups in 1 gallon, so 3 gallons of punch would be equal to:
3 gallons x 16 cups/gallon = 48 cups
If each serving size is 1/2 cup, then the number of servings in 3 gallons of punch would be:
48 cups / (1/2 cup/serving) = 96 servings
Therefore, 3 gallons of punch would provide 96 servings, assuming each serving size is 1/2 cup.
point A is at (4,7). Find its new coordinate after it is translated 3 units left and 2 units down
A. (4,2)
B. (1,5)
C. (7, -4)
D. (-5,3)
E. (3,4)
Answers
Answer:
B 1,5
Step-by-step explanation:
Answer:
b.(1,5)
Step-by-step explanation:
evaluate the expression (− 4.8)− 9 ⋅ (− 4.8)9
Answers
The approximate value of the expression (−4.8)−9 ⋅ (−4.8)9 is 0.99999999735.
To evaluate the expression (−4.8)−9 ⋅ (−4.8)9, we need to follow the order of operations, which is parentheses, exponents, multiplication/division (from left to right), and addition/subtraction (from left to right).
Let's break down the expression step by step:
(−4.8)−9 means raising −4.8 to the power of -9.
First, let's calculate (−4.8)−9:
(−4.8)−9 = 1 / (−4.8)9 (since a negative exponent signifies taking the reciprocal of the base)
Now, let's calculate (−4.8)9:
(−4.8)9 ≈ -11084.4720416 (using a calculator or computational tool to perform the exponentiation)
Substituting this value back into the previous step:
(−4.8)−9 = 1 / (−4.8)9 ≈ 1 / (-11084.4720416) ≈ -9.017218987 × \(10^{(-5)\)
Next, let's move on to the second part of the expression:
(−4.8)−9 ⋅ (−4.8)9 = (-9.017218987 × \(10^{(-5)\)) × (-11084.4720416)
Calculating the multiplication:
(-9.017218987 × \(10^{(-5)\)) × (-11084.4720416) ≈ 0.99999999735
Therefore, the approximate value of the expression (−4.8)−9 ⋅ (−4.8)9 is 0.99999999735.
for such more question on expression
https://brainly.com/question/16763767
#SPJ8
Faizah is paid $11 per hour for her work at a factory. She works 9 hours a day and 24 days a month. She saves $594 a month. Express the amount she saves as a percentage of her income.
Answers
Answer:
The amount she saves is 25% of her income
Step-by-step explanation:
She is paid $11 per hour
She works 9 hours per day
and for 24 days per month
So, she works 9(24) hours per month
= 216 hours per month
Now, she is paid $11 hourly, so for 216 hours,
she will have 11(216) = $2376
Total income = $2376 per month
Saving = $594 per month
As a percentage, we divide the savings by the total income,
savings/(total income) = 594/2376 = 1/4 = 0.25
Hence we get 25%
An automotive insurance company wants to predict which filed stolen vehicle claims are fraudulent, based on the mean number of claims submitted per year by the policy holder and whether the policy is a new policy, that is, is one year old or less (coded as 1 = yes, 0 = no). Data from a random sample of 98 automotive insurance claims, organized and stored in show that 49 are fraudulent (coded as 1) and 49 are not (coded as 0). (Data extracted from A. Gepp et al., "A Comparative Analysis of Decision Trees vis-a-vis Other Computational Data Mining Techniques in Automotive Insurance Fraud Detection, " Journal of Data Science, 10 (2012), pp. 537-561.) a. Develop a logistic regression model to predict the probability of a fraudulent claim, based on the number of claims submitted per year by the policy holder and whether the policy is new. b. Explain the meaning of the regression coefficients in the model in (a). c. Predict the probability of a fraudulent claim given that the policy holder has submitted a mean of one claim per year and holds a new policy. d. At the 0.05 level of significance, is there evidence that a logistic regression model that uses the mean number of claims submitted per year by the policy holder and whether the policy is new to predict the probability of a fraudulent claim is a good fitting model? e. At the 0.05 level of significance, is there evidence that the mean number of claims submitted per year by the policy holder and whether the policy is new each makes a significant contribution to the logistic model? f. Develop a logistic regression model that includes only the number of claims submitted per year by the policy holder to predict the probability of a fraudulent claim. g. Develop a logistic regression model that includes only whether the policy is new to predict a fraudulent claim. h. Compare the models in (a), (f). and (g). Evaluate the differences among the models.
Answers
The logistic regression model developed predicts the probability of a fraudulent claim based on the mean number of claims submitted per year by the policy holder and whether the policy is new. The regression coefficients in the model provide insights into the relationship between the predictor variables and the probability of a fraudulent claim.
In this context, the regression coefficient for the mean number of claims per year indicates the change in the log-odds of a fraudulent claim for each unit increase in the mean number of claims. A positive coefficient suggests that as the mean number of claims per year increases, the probability of a fraudulent claim also increases. Conversely, a negative coefficient would indicate a negative relationship.
The regression coefficient for the policy being new (coded as 1) versus not new (coded as 0) represents the difference in the log-odds of a fraudulent claim between the two groups. A positive coefficient indicates that holding a new policy is associated with a higher probability of a fraudulent claim compared to holding an older policy.
To predict the probability of a fraudulent claim given a mean of one claim per year and a new policy, we can substitute these values into the logistic regression equation and calculate the predicted probability using the model's coefficients.
To determine if the logistic regression model is a good fit, we can perform a hypothesis test at a significance level of 0.05. This test evaluates whether the model's coefficients are significantly different from zero, indicating a significant relationship between the predictors and the probability of a fraudulent claim.
To assess the contributions of the mean number of claims per year and the policy being new to the logistic model, we can perform another hypothesis test at a significance level of 0.05. This test examines whether each predictor variable individually makes a significant contribution to the model's prediction.
Comparing the models that include both predictors, only the mean number of claims per year, or only the policy being new allows us to evaluate the impact of including or excluding each variable on the model's performance and predictive accuracy. This analysis helps understand the relative importance of the predictors in identifying fraudulent claims.
Learn more about The logistic
brainly.com/question/32571029
#SPJ11
determine whether rolle's theorem applies to the function shown below on the given interval. if so, find the point(s) that are guaranteed to exist by rolle's theorem. f(x)=x(x−10)2; [0,10]
Answers
The function must satisfy f(0) = f(10), which is true. By Rolle's theorem, there exists a number c in (0, 10) such that f'(c) = 0. We have found that f'(x) = (x-10)(3x-10), which equals 0 at x = 10/3 and x = 10. But 10/3 is not in [0, 10]. Therefore, the only point guaranteed to exist by Rolle's Theorem is x = 10.
To determine whether Rolle's theorem applies to the given function f(x)=x(x-10)^2 on the given interval [0, 10] and to find the point(s) that are guaranteed to exist by Rolle's theorem. Rolle's Theorem states that if a function f is continuous on a closed interval [a, b] and differentiable on the open interval (a, b) and f(a) = f(b), then there exists a number c in (a, b) such that f'(c) = 0.
Therefore, the function must be continuous on the interval [0, 10] and differentiable on the open interval (0, 10).The function f(x) = x(x-10)^2 is continuous on the interval [0, 10] and differentiable on the open interval (0, 10). Therefore, Rolle's Theorem applies to the given function on the interval [0, 10].Now, we can apply Rolle's Theorem and find the point(s) that are guaranteed to exist by it.
Therefore, f'(x) = 0 at x= 10/3 or x = 10. But, 10/3 is not in the interval [0, 10]. Hence, the only point guaranteed to exist by Rolle's Theorem is x = 10.
To know more about function visit :
https://brainly.com/question/30594198
#SPJ11
A donut shop has made 36 chocolate donuts, 27 strawberry donuts and 18 caramel donuts. The donut shop wants to sell boxes with a combination of the three types of donuts. How many boxes will there be and how many of each donut will there be in each box if each box has the same total number of donuts? Pls show working. Thx.
Answers
Each box will contain 1 chocolate donut, 1 strawberry donut, and 1 caramel donut, there will be a Total of 4 boxes, and each box will contain 1 chocolate donut, 1 strawberry donut, and 1 caramel donut.
The number of boxes and the distribution of donuts in each box, we need to find the greatest common divisor (GCD) of the total number of chocolate, strawberry, and caramel donuts available. The GCD will represent the maximum number of donuts that can be included in each box.
First, let's find the GCD of 36, 27, and 18. By calculating the GCD, we can determine the maximum number of donuts that can be included in each box.
GCD(36, 27, 18) = 9
Therefore, the maximum number of donuts that can be included in each box is 9.
Next, we need to determine the number of boxes. To do this, we divide the total number of each donut type by the maximum number of donuts per box.
Number of boxes for chocolate donuts = 36 / 9 = 4 boxes
Number of boxes for strawberry donuts = 27 / 9 = 3 boxes
Number of boxes for caramel donuts = 18 / 9 = 2 boxes
Since each box contains the same total number of donuts, we can conclude that there will be 4 boxes with chocolate donuts, 3 boxes with strawberry donuts, and 2 boxes with caramel donuts.
To find the distribution of donuts in each box, we divide the maximum number of donuts per box by the GCD:
Distribution in each box: 9 = 1 × 9
Therefore, each box will contain 1 chocolate donut, 1 strawberry donut, and 1 caramel donut, there will be a total of 4 boxes, and each box will contain 1 chocolate donut, 1 strawberry donut, and 1 caramel donut.
For more questions on Total .
https://brainly.com/question/30612486
#SPJ8
Pls Help! Will Mark Brainliest!!!

Answers
Step-by-step explanation:
it is a bit unclear to me how the cups are stacked on each other.
are we building a pyramid or is it really just one line of cups stacked into each other ? the equation suggests the latter. so, I will continue with that assumption.
then each additional cup really adds only the height of the rim to the total height of the cup tower.
so, we want to find out for what smallest x is the equation delivering as y value 32,400 or more.
32,400 = 2.4x + 13.6
let's get rid of the decimals by multiplying everything by 10.
324,000 = 24x + 136
323,864 = 24x
x = 323,864/24 = 13,494.33333...
so, we need 13,495 cups to reach its height (just rounding it to 13,494 would still leave a tiny gap, so we need the 13,495th cup - there is no way to reach the height exactly).
What is a best estimate for 320/11
This is worth 65 points

Answers
Step-by-step explanation:
We can estimate 320/11 by using 320/10, which is 32.
Making it divide by 10 is easier as compared to 11.
Can anyone simplify
5y + 4x +5x
Answers
Answer:
5y+9x is the simplified version
How many more minutes can mate car travel per gallon of gas then jenna's car
Answers
Mate's car can travel approximately 5 more minutes per gallon of gas compared to Jenna's car.
To determine how many more minutes Mate's car can travel per gallon of gas compared to Jenna's car, we would need additional information about the fuel efficiency or miles per gallon (MPG) for each car.
Fuel efficiency is typically measured in terms of miles per gallon, indicating the number of miles a car can travel on a gallon of gas.
To calculate the difference in travel time, we would also need to know the average speed at which the cars are traveling.
Once we have the MPG values for Mate's car and Jenna's car, we can calculate the difference in travel time per gallon of gas by considering their respective fuel efficiencies and average speeds.
If Mate's car has a fuel efficiency of 30 MPG and Jenna's car has a fuel efficiency of 25 MPG, we can calculate the difference in travel time by comparing the distances they can travel on a gallon of gas.
Let's assume both cars are traveling at an average speed of 60 miles per hour.
For Mate's car:
Travel time = Distance / Speed
= (30 miles / 1 gallon) / 60 miles per hour
= 0.5 hours or 30 minutes.
For Jenna's car:
Travel time = Distance / Speed
= (25 miles / 1 gallon) / 60 miles per hour
= 0.4167 hours or approximately 25 minutes.
Without specific information about the MPG values and average speeds of the cars, it is not possible to provide an accurate answer regarding the difference in travel time per gallon of gas between Mate's car and Jenna's car.
For similar questions on Mate's car
https://brainly.com/question/33586007
#SPJ8
What is the exponent in the power of 10?
Answers
1. Find the missing measure in the triangle below.
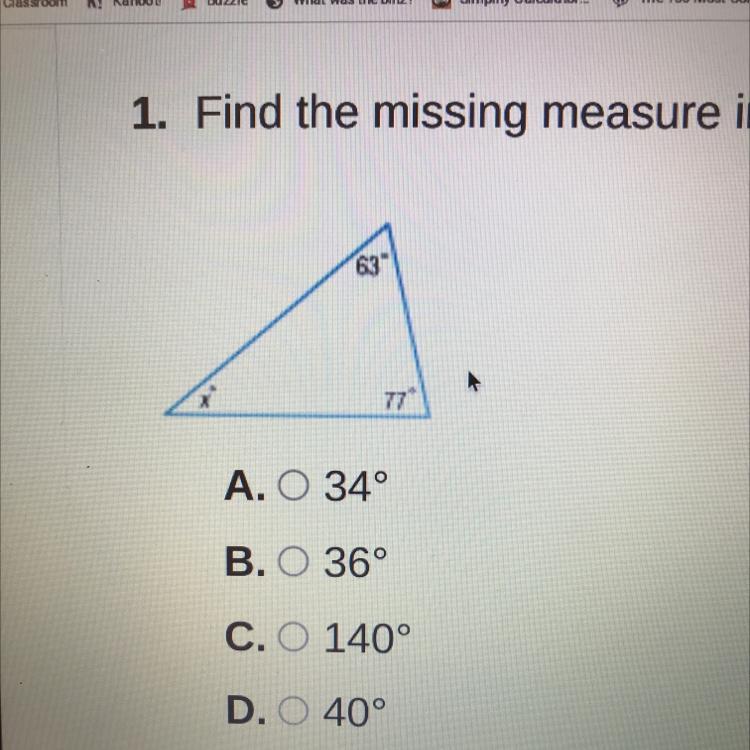
Answers
Answer: i think it’s 40
Step-by-step explanation: triangle has to be 180° according to the internet and 77 plus 63 is 140 plus 40 would be 180
a large software company gives job applicants a test of programming ability and the mean for that test has been 160 in the past. twenty-five job applicants are randomly selected from one large university and they produce a mean score and standard deviation of 183 and 12, respectively. use a 0.05 level og significance to test the claim that this sample comes from a population with a mean score greater than 160. use the P-value method of testing hypotheses.
Answers
Using the P-value method of testing hypotheses with a significance level of 0.05, the sample provides strong evidence to support the claim that the mean score of job applicants from the university is greater than 160.
To test the claim that the mean score of job applicants from the university is greater than 160, we will perform a one-sample t-test using the P-value method. The null hypothesis (H0) assumes that the mean score is equal to 160, while the alternative hypothesis (Ha) assumes that the mean score is greater than 160.
First, we calculate the test statistic, which is the t-value. The formula for the t-value is:
t = (sample mean - hypothesized mean) / (sample standard deviation / sqrt(sample size))
Plugging in the given values, we have:
t = (183 - 160) / (12 / √(25))
= 23 / (12 / 5)
= 23 * (5 / 12)
≈ 9.58
Next, we find the P-value associated with the test statistic. The P-value represents the probability of obtaining a test statistic as extreme as the observed value, assuming the null hypothesis is true. Since the alternative hypothesis is one-sided (greater than 160), we calculate the P-value by finding the probability of the t-distribution with 24 degrees of freedom being greater than the calculated t-value.
Consulting statistical tables or using software, we find that the P-value is very small (less than 0.0001).
Since the P-value (less than 0.0001) is less than the significance level (0.05), we reject the null hypothesis. This provides strong evidence to support the claim that the mean score of job applicants from the university is greater than 160.
Learn more about P-value
brainly.com/question/30461126
#SPJ11
bowl 1 has 5 red and 5 green balls. bowl 2 has 6 red and 4 green balls. a bowl is selected at random and a ball is drawn at random. it turns out to be g. what is the probability that it came from bowl 2?
Answers
The probability that a green ball is chosen from bowl two is 4/9 using Baye's Theorem.
Let M be the event that the ball is green.
Let A be the event that the ball is drawn from bowl one and event b from bowl two.
Bowl one has 5 red balls and 5 green balls. And bowl two has 6 red balls and 4 balls.
Total number of red balls = 5 + 6 = 11
Total number of green balls = 5+ 4 = 9
Total number of balls in bowl one = 5+ 5 = 10
Total number of balls in bowl two = 6 + 4 =10
P(A) = 1/2 = P(B)
P(M/A) = 5/10
P( M/B) = 4/10
A bowl is selected at random and a ball is drawn at random.
Using Baye's Theorem we can solve the problem as,
Probability that ball is chosen is green drawn from bowl two , P(B/M)
= \(\frac{[P(B)P(M/B)]}{[ { P(A)(M/A)} + {P(B)(M/B)}]}\)
= \(\frac{ [ (1/2)(4/10)]}{ [ (1/2)(5/10) + (1/2)(4/10)]}\)
= 4/9
To know more about Baye's theorem here
https://brainly.com/question/29598596
#SPJ4
a researcher finds a 0.31 pearson r correlation between amount of time it takes to complete a puzzle and iq scores for 97 adult participants. what is the correct decision about the null hypothesis test?
Answers
It can be concluded that there is a significant positive correlation between the time it takes to complete a puzzle and the IQ scores of these participants.
To determine the correct decision about the null hypothesis test, we need to compare the calculated Pearson's correlation coefficient (r) of 0.31 to a critical value based on the sample size and level of significance.
Assuming a significance level of 0.05 (or alpha = 0.05) and a two-tailed test, we can use a t-distribution with degrees of freedom (df) equal to n-2, where n is the sample size. For a sample size of 97, df = 95.
Using a table or calculator, we can find the critical t-value that corresponds to a significance level of 0.05 and 95 degrees of freedom. The critical t-value is approximately 1.984.
Next, we can calculate the t-value for the observed correlation coefficient using the formula:
\(t = r * sqrt(n-2) / sqrt(1-r^2)\)
where r is the observed correlation coefficient and n is the sample size.
Plugging in the values, we get:
t = 0.31 * sqrt(97-2) / sqrt(1-0.31^2) = 3.23
The absolute value of the calculated t-value (3.23) is greater than the critical t-value (1.984), indicating that the correlation coefficient is statistically significant. In other words, there is strong evidence to reject the null hypothesis, which states that there is no correlation between the time it takes to complete a puzzle and the IQ scores of the adult participants.
Therefore, we can conclude that there is a significant positive correlation between the time it takes to complete a puzzle and the IQ scores of these participants. However, we cannot make any causal claims based on this correlation alone, as there may be other variables that could explain the relationship.
Learn more about correlation at
brainly.com/question/28898177
#SPJ4
One quart of cranberry juice equals 4 cups. How many quarts of cranberry juice is needed for the recipe? If you can only buy whole quarts of juice, will there be cranberry juice left over?
Answers
Answer:
you have to provide the recipie
Step-by-step explanation:
For her final project, stacy plans on surveying a random sample of students on whether they plan to go to florida for spring break. From past years, she guesses that about % of the class goes. Is it reasonable for her to use a normal model for the sampling distribution of the sample proportion? why or why not?.
Answers
Yes, it is reasonable for her to use a normal model for the sampling distribution of the sample proportion. In this case, less than ten efforts have been successful. Since 5 is a lot less than 10, this is the case.
Because the data don't fit the success and failure criteria, it is not appropriate to adopt a normal model for a sampling of the sample distribution.
50 students make up the sample. The probability that she assumes 10% of the group will attend is 10%.
It will be demonstrated by:
1 - p = 1 - 10% = 1 - 0.10 = 0.90
np = 50 × 0.1 = 5. This suggests the number of victories.
Less than 10 attempts have succeeded in this instance. 5 is much less than 10, hence this case. As a result, the data does not satisfy the requirement.
Learn more about the sampling at
https://brainly.com/question/28941407?referrer=searchResults
#SPJ4
The question is -
For her final project, Stacy plans on surveying a random sample of 50 students on whether they plan to go to Florida for spring break. from past years, she guesses that about 10% of the class goes. is it reasonable for her to use a normal model for the sampling distribution of the sample proportion? why or why not?