Answers
The number of square meters of paint needed to cover the surface is 149.90m²
Surface area of composite solidsFrom the question, we are to determine the number of square meters of paint needed to cover the surfaces
The number of square meters of paint needed to cover the surfaces is equal to the surface area of the solid
To do this, we will calculate the surface area of the composite solid
Surface area of the composite solid = \(\pi r^{2} + 2\pi rh_{c} + 2(lh_{b} + wh_{b} ) + lw-\pi r^{2}\)
Surface area of the composite solid = \(2\pi rh_{c} + 2(lh_{b} + wh_{b} ) + lw\)
Where r is the radius of the cylindrical top
\(h_{c}\) is the height of the cylindrical top
\(l\) is the length of the box
\(h_{b}\) is the height of the box
\(w\) is the width of the box
From the given information,
r = 2 m
\(h_{c}\) = 3 m
\(l\) = 4 m
\(h_{b}\) = 2.4 m
\(w\) = 5 m
Put the parameters into the equation,
Surface area of the composite solid = \((2\pi \times 2 \times 3) + 2(9\times2.4 + 5\times2.4) + 9\times5\)
\(= 12\pi +112.2\)
\(= 37.699 +112.2\)
\(= 149.899\) m²
≅ 149.90 m²
∴ Surface area of the composite solid ≅ 149.90 m²
Hence, the number of square meters of paint needed to cover the surface is 149.90m²
Learn more on Surface area of composite solid here: https://brainly.com/question/23817907
#SPJ1
Related Questions
4x^2-4x=+1 by factoring
Answers
Answer:
Below.
Step-by-step explanation:
4x^2 - 4x - 1 = 0
This will not factor.
But 4x^2 - 4x + 1 = 0 will:
= (2x - 1)(2x - 1) = 0
x = 0.5 (*2)
Tyrone saw the equation 4X = 2 - 4 - 3x match the property with each of Tyrone steps for solving the equation
Answers
The correct property should be matched with each of Tyrone's steps for solving the equation as follows:
4x = 2 - 8 + 12x ⇒ distributive property
4x = -6 + 12x ⇒ subtraction property of equality.
-8x = -6 ⇒ combine like terms.
x = 3/4 ⇒ division property of equality.
What is the distributive property of multiplication?The distributive property of multiplication states that when the sum of two or more addends are multiplied by a particular numerical value, the same result (output) would be obtained as when each addend is multiplied respectively by the same numerical value, and the products are added together.
Mathematically, the distributive property of multiplication can be represented by this expression:
a(b + c) = ab + ac.
By applying the distributive property of multiplication in step 1, we have:
4x = 2 - 4(2 - 3x)
4x = 2 - 8 + 12x
By applying the subtraction property of equality in step 2, we have:
4x = -6 + 12x
Next, we would combine like terms in step 3 as follows:
4x - 12x = -6
-8x = -6
By applying the division property of equality in step 4, we have:
x = 6/8
x = 3/4.
Read more on distributive property here; brainly.com/question/24014491
#SPJ1

A test score in the 3rd percentile would be considered ______. a. about average b. very high c. cannot be determined d. very low
Answers
Answer:
Very low, as it means that 97% of people scored the same or higher than you.
7. Myxomatosis kills 92% of a colony of 300
rabbits. How many rabbits survive?
Answers
Answer: In 1858 twelve pairs of the European rabbit were released on a ranch in of mosquitoes only 90 per cent of the remaining population was killed
Step-by-step explanation:
Volume = 154 cm cubic
height = 16 cm
d = ?
FIND THE DIAMETER OF THE CYLINDER
#SHOW THE WORKING PLZZ
Answers
Cylinder Volume
Level : JHSV = hπr²
154 cm³ = 16 cm × 3.14 × r²
154 cm³ = 50.28 cm × r²
r² = 154 cm³ : 50.28 cm
r² = 3.0625 cm²
r = 1.75 cm
d = 2r
d = 2 × 1.75 cm
d = 3.5 cm
So, the diameter of the Cylinder is 3.5 cm
#LearnWithEXO
help me with this please !! i need this done by tomorrow!!

Answers
Excuse my poor drawing skills, but I made a graph and a drawing of what I mean.

Scott types at a rate of 10 words per minute. How many words does he type in 5 minutes?
Answers
Answer: 50 words per minute
Step-by-step explanation: if he types 10 words per minute and if you multiply that by 5 the answer is 50 words per minute
Step by step
The best way to do this is to set up your equation and cross multiply
You know 10 wpm/1 minute = x /5 minutes
Cross multiply and you get x = 50
I gave you an attachment to show the cross multiply

if there are 2 blue, 5 yellow, and 3 white marbles in a bag, what is the white marbles in a bag what is the probability of pulling a blue marble from the bag

Answers
Answer:
The probability of pulling a blue marble from the bag is;
\(P_B=\frac{1}{5}=0.2\)Explanation:
Given that there are 2 blue, 5 yellow, and 3 white marbles in a bag.
The total number of marbles in the bag is;
\(n_t=2+5+3=10\)The probability of pulling a blue marble from the bag will be;
\(P_B=\frac{\text{ number of blue marble}}{\text{total number of marble}}\)Substituting the given values;
\(\begin{gathered} P_B=\frac{\text{ number of blue marble}}{\text{total number of marble}}=\frac{2}{10} \\ P_B=\frac{1}{5}=0.2 \end{gathered}\)Therefore, the probability of pulling a blue marble from the bag is;
\(P_B=\frac{1}{5}=0.2\)If Malik purchases an iced coffee drink for $5.69 and leaves a $1 tip, what percentage did he tip?
Answers
Answer:
Malik tipped a 17.5% tip. You could also say he tipped a 17.6% tip depending on how you round. Both answers get you a dollar.
An experimenter would like to construct a 99% confidence interval with a width at most 0. 5 for the average resistance of a segment of copper cable of a certain length. If the experimenter knows that the standard deviation of such resistances is 1. 55. How big a sample should the experimenter take from the population? what happens if the standard deviation and the width of the confidence interval are both doubled?.
Answers
A big sample that should the experimenter take from the population is 256 and if the standard deviation and the width of the confidence interval are both doubled then the sample is also 256.
In the given question,
The confidence level = 99%
Given width = 0.5
Standard deviation of resistance(\(\sigma\))= 1.55
We have to find a big sample that should the experimenter take from the population and what happens if the standard deviation and the width of the confidence interval are both doubled.
The formula to find the a big sample that should the experimenter take from the population is
Margin of error(ME) \(=z_{\alpha /2}\frac{\sigma}{\sqrt{n}}\)
So n \(=(z_{\alpha /2}\frac{\sigma}{\text{ME}})^2\)
where n=sample size
We firstly find the value of ME and \(z_{\alpha /2}\).
Firstly finding the value of ME.
ME=Width/2
ME=0.5/2
ME=0.25
Now finding the value of \(z_{\alpha /2}\).
Te given interval is 99%=99/100=0.99
The value of \(\alpha\) =1−0.99
The value of \(\alpha\) =0.01
Then the value of \(\alpha /2\) = 0.01/2 = 0.005
From the standard table of z
\(z_{0.005}\) =2.58
Now putting in the value in formula of sample size.
n\(=(2.58\times\frac{1.55}{0.25})^2\)
Simplifying
n=(3.999/0.25)^2
n=(15.996)^2
n=255.87
n≈256
Hence, the sample that the experimenter take from the population is 256.
Now we have to find the sample size if the standard deviation and the width of the confidence interval are both doubled.
The new values,
Standard deviation of resistance(\(\sigma\))= 2×1.55
Standard deviation of resistance(\(\sigma\))= 3.1
width = 2×0.5
width = 1
Now the value of ME.
ME=1/2
ME=0.5
The z value is remain same.
Now putting in the value in formula of sample size.
n\(=(2.58\times\frac{3.1}{0.5})^2\)
Simplifying
n=(7.998/0.5)^2
n=(15.996)^2
n=255.87
n≈256
Hence, if the standard deviation and the width of the confidence interval are both doubled then the sample size is 256.
To learn more about confidence interval link is here
brainly.com/question/24131141
#SPJ4
Joe earned x dollars the first day he worked in December, where x is an integer. For each day after the first that he worked in December, Joe earned twice the amount he earned on the previous day. Did Joe earn less than $35 on the 4th day he worked in December?
(1) Joe earned more than $120 in total for the first five days he worked in December.
(2) Joe earned less than $148 on the 6th day he worked in December.
Answers
Answer:
1. Always translate the question stem, set up equations (limit the number of variables) and breakdown the question stem of possible
2. Never overlook the constraints the question provides.
Now the question stem tells us that on the
1st day Joe earned = x
2nd day = 2x
3rd day = 4x
4th day = 8x
Question stem: Did Joe earn less than $35 on the 4th day -----> 8x < 35 ----> x < 4.375
Since x is an integer, the question becomes 'Is x <= 4
Statement 1 : Joe earned more than $120 in total for the first five days he worked in December.
x + 2x + 4x + 8x + 16x > 120
31x > 120 ---> x > 3.9....
This gives us both a YES and a NO since x can be 4 or any integer greater than 4
Statement 2: Joe earned less than $148 on the 6th day he worked in December
32x < 148 ----> x < 4.625
Since x is an integer, x <=4. Sufficient.
hope this helps
-lvr
what is the integral of ∫4x^2 dx
Answers
Answer:
\(\boxed{\frac{4}{3} x^3 + c}\)
Step-by-step explanation:
\(\int\limits {4x^2} \ dx\)
\(= \frac{4}{3} x^3 + c\)
the aswers is 4/3 x³ + c
okey fine
Find the equation of a line that passes through the points (1,-3) and (3,-4).
Answers
\((\stackrel{x_1}{1}~,~\stackrel{y_1}{-3})\qquad (\stackrel{x_2}{3}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-4}-\stackrel{y1}{(-3)}}}{\underset{\textit{\large run}} {\underset{x_2}{3}-\underset{x_1}{1}}} \implies \cfrac{-4 +3}{2} \implies \cfrac{ -1 }{ 2 } \implies - \cfrac{ 1 }{ 2 }\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-3)}=\stackrel{m}{- \cfrac{ 1 }{ 2 }}(x-\stackrel{x_1}{1}) \implies y +3 = - \cfrac{ 1 }{ 2 } ( x -1) \\\\\\ y+3=- \cfrac{ 1 }{ 2 }x+\cfrac{1}{2}\implies y=- \cfrac{ 1 }{ 2 }x+\cfrac{1}{2}-3\implies {\Large \begin{array}{llll} y=- \cfrac{ 1 }{ 2 }x-\cfrac{5}{2} \end{array}}\)
Answer: First, let's find the slope of the line:
slope = (change in y) / (change in x)
slope = (-4 - (-3)) / (3 - 1)
slope = -1/2
Now, let's choose one of the points, say (1,-3), and use the point-slope formula:
y - y1 = m(x - x1)
where m is the slope and (x1, y1) are the coordinates of the point.
So, substituting in the values we get:
y - (-3) = (-1/2)(x - 1)
Simplifying this equation, we get:
y + 3 = (-1/2)x + 1/2
Subtracting 3 from both sides, we get:
y = (-1/2)x - 5/2
Therefore, the equation of the line that passes through the points (1,-3) and (3,-4) is y = (-1/2)x - 5/2.
Your welcome.
Step-by-step explanation:
Is the difference of 18 and 3 a rational number?
Answers
Answer:
it is a whole number but because rational numbers include all intergers and whole numbers it is also a rational number
Step-by-step explanation:
What is the value of the expression 12 x (-1.6)
Answers
Answer: -19.2
Step-by-step explanation:
Select the mean, median, mode and range of the following list of values.1, 2, 4,7Averages3.5None36MeanMedianRangeMode
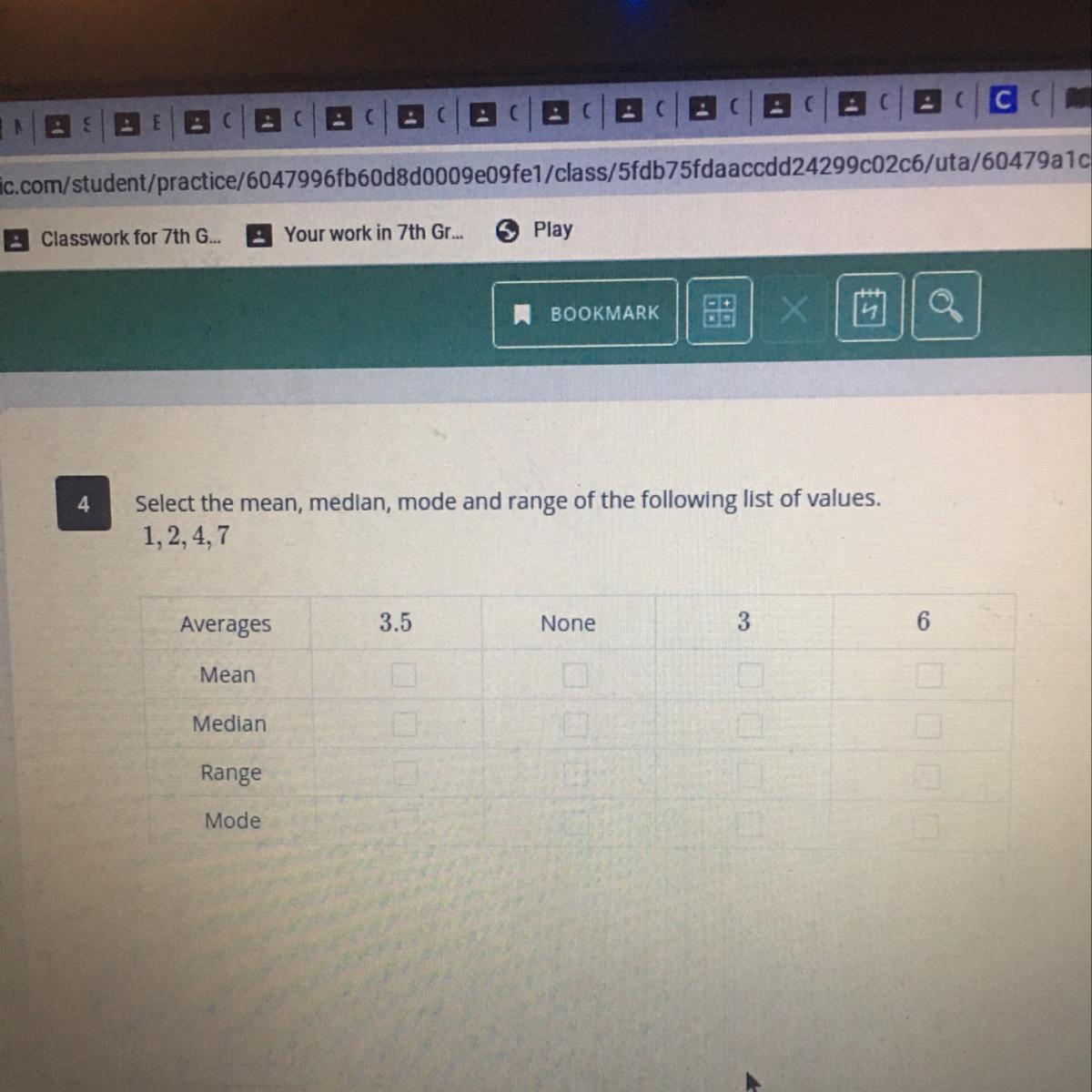
Answers
The data set is
1, 2, 4, 7
The answers are;
\(\begin{gathered} \text{Mean}=\frac{1+2+4+7}{4} \\ \text{Mean}=\frac{14}{4} \\ \text{Mean}=3.5 \end{gathered}\)\(\begin{gathered} \text{Median}=\frac{2+4}{2} \\ \text{Median}=\frac{6}{2} \\ \text{Median}=3 \end{gathered}\)The median in a case where the data set is an even number, then the median would take account of both middle values and then calculate addition of both and then divide by 2
The Mode is the most frequently occuring value in the data set. In this case, all observed data occur just once, and none of them occur more than once. Hence there is no Mode
\(\begin{gathered} \text{Range}=\text{Highest value-Lowest value} \\ Range=7-1 \\ \text{Range}=6 \end{gathered}\)Kate invests £2000 in a savings account for 3 years the account pays compound interest at an annual rate of 2. 5% for the first year x% for the second year x% for the third year there is a total amount of £2124. 46 in the savings account at the end of 3 years work out the rate of interest in the second year
Answers
The second year's interest rate is 1.80%.
Compound interest is defined as Since compound interest accrues and is added to the accrued interest from earlier periods, borrowers are expected to pay interest on interest in addition to principal.
We are aware that the compound interest formula is,
A = P(1 + r/100)ⁿ.
Where A is the amount, P is the principle, r is the rate, and n is the number of years.
Given, Katy places $2000 over a three-year period in a savings account.
For the first year, the account offers compound interest at a 2.5% annual rate.
∴ A = 2000(1 + 2.5/100)¹.
A = 2000(1.025). (1.025).
A = 2050.
It now earns x% for the second year.
∴ 2050(1+x/100)² = 2124.46
(1+x/100)² =2124.46/2050
1+x/100 =√(2124.46/2050)
x/100 = √(2124.46/2050) -1
x = (√(2124.46/2050) -1)*100
x = 1.80%.
the interest is 1.80 percent
learn more about compound interest here :
brainly.com/question/29335425
#SPJ4
try to add all categorical variables to create a linear regression model. which variable cannot be added (not allowed by the software) and why is that?
Answers
There are a few different reasons why certain categorical variables may not be allowed in a linear regression model:
Some software packages require categorical variables to be converted to numerical variables before they can be included in a linear regression model. This is typically done using one-hot encoding, where each category is represented by a binary variable indicating whether or not it is present.
If the number of categories for a given variable is very large, this can create a very large number of new variables, which may exceed the capacity of the software or the memory available on the computer running the analysis.
Some software packages may not allow categorical variables with a very large number of categories, again because of the potential computational demands of encoding these variables as binary variables.
If a categorical variable has a large number of categories relative to the sample size, it may not be possible to estimate the coefficients for each category with enough precision to be useful. Some software packages may not allow categorical variables with missing values, unless those missing values are explicitly coded as a category.
Overall, the decision to include or exclude categorical variables from a linear regression model will depend on a variety of factors, including the number of categories, the software being used, the size of the dataset, and the research question being addressed.
For more details about variables click here:
https://brainly.com/question/17344045#
#SPJ11
Watch help video Find the length of the third side. If necessary, write in simplest radical form. 7 4√2
Answers
In simplest radicle form, the length of the third side = 9 units.
Given,
Side A = 7 units.
Side B = 4√2 units.
To find Side C, we use the Pythagorean formula,
a² = b² + c²
7² = \(4\sqrt{2}^{2}\) + c²
c² = 49 + 32
c² = 81
√c² = √81
c = -9,9.
c ≠ -9 as negative values are not considered for dimensions.
Hence, the length of the third side is 9 units.
To learn more about Pythagorean theory, refer to:
https://brainly.com/question/343682
#SPJ4
Your question is incomplete. The complete question is:
With reference to the figure below, find the length of the third side. If necessary, write in the simplest radical form.

I've been having problems with this and I was wondering if someone could give me the answers 1 - 5

Answers
The measures of x are obtained with the Pythagorean Theorem, as follows:
1. x = 10.2.
2. x = 7.2.
3. x = 13.7.
4. x = 36.2.
5. x = 10.7.
What is the Pythagorean Theorem?The Pythagorean Theorem is a geometry axiom which states that for a right triangle, the length of the hypotenuse squared is equals to the sum of the lengths of the sides squared.
Hence, for item 1, we have that:
x² + 16² = 19²
x = square root(19² - 16²)
x = 10.2.
For item 2, we have that:
x² + 12² = 14²
x = square root(14² - 12²)
x = 7.2.
For item 3, we have that:
x² + 9.2² = 16.5²
x = square root(16.5² - 9.2²)
x = 13.7.
For item 4, we have that:
The bottom side is bisected into two equal sides of dimension 15.Then x is the hypotenuse of a right triangle of sides 15 and 33, thus:x² = 15² + 33²
x = square root(15² + 33²)
x = 36.2.
For item 5, first we find the side of the top right triangle, hence:
h² + 16² = 25²
h = square root(25² - 16²)
h = 19.2.
Then the value of x is obtained as follows:
x² + 19.2² = 22²
x = square root(22² - 19.2²)
x = 10.7.
More can be learned about the Pythagorean Theorem at https://brainly.com/question/28853425
#SPJ1
A square and a regular hexagon have sides of the same length. the perimeter of the square increased by 32 units will be equal to the perimeter of the hexagon. what is x, the length of a side of the hexagon or square?
Answers
The length of a side of the hexagon or square is - 16 units
A square has four equal sides and four equal angles. The angles of squares are at right angles or 90°.If all six sides are equal, then it is called a regular hexagon. The perimeter of the regular hexagon is defined as the sum of all the sides of a hexagon.The length of a side of the hexagon or square = x
The perimeter of the square = 4 × lengths of its side
= 4x
The perimeter of the hexagon = 6 × lengths of its side
= 6x
According to the question,
4x + 32 = 6x
⇒ 6x - 4x = 32
⇒ 2x = 32
⇒ x = 16
So, the length of a side of the hexagon or square is - 16 units.
Read more about square :
https://brainly.com/question/25092270
#SPJ4
Bryan has a collection of baseball cards which he shares equally with his brother, Jude. Bryan also received five cards from his friend, Gene. If Bryan has 12 baseball cards now, how many cards did he originally have in his collection?
Answers
Answer:
7
Step-by-step explanation:
Answer:
x = 7
Step-by-step explanation:
I NEED HELPPPPP. SOMEONE ANSWER THISSSS

Answers
Answer:y=415 x = 21.5
Step-by-step explanation:
We can see 4x-37 = 49
4x = 86
x = 21.5
4(21.5) -3 = 83
Then we can see what the other side is because they are equal
y/5 = 83
83 x 5 = 415
y=415
Explanation
Models of inventory systems frequently consider the relationships among a beginning inventory,
a production quantity, a demand or sales, and an ending inventory. For a given
production period j, let
sj-1 = ending inventory from the previous period (beginning inventory for period j)
xj = production quantity in period j
dj = demand in period j
sj = ending inventory for period j
a. Write the mathematical relationship or model that shows ending inventory as a function
of beginning inventory, production, and demand.
b. What constraint should be added if production capacity for period j is given by Cj?
c. What constraint should be added if inventory requirements for period j mandate an
ending inventory of at least Ij?
Answers
a. This equation states that the ending inventory for period j (sj) is equal to the beginning inventory from the previous period (sj-1) plus the production quantity in period j (xj), minus the demand in period j (dj).
b. This constraint ensures that the production quantity in period j (xj) does not exceed the production capacity for that period (Cj).
c. This constraint ensures that the ending inventory for period j (sj) is greater than or equal to the required inventory level for that period (Ij).
a. The mathematical relationship or model that shows ending inventory as a function of beginning inventory, production, and demand can be represented as:
sj = sj-1 + xj - dj
This equation states that the ending inventory for period j (sj) is equal to the beginning inventory from the previous period (sj-1) plus the production quantity in period j (xj), minus the demand in period j (dj).
b. If the production capacity for period j is given by Cj, the constraint that should be added is:
xj ≤ Cj
This constraint ensures that the production quantity in period j (xj) does not exceed the production capacity for that period (Cj).
c. If inventory requirements for period j mandate an ending inventory of at least Ij, the constraint that should be added is:
sj ≥ Ij
This constraint ensures that the ending inventory for period j (sj) is greater than or equal to the required inventory level for that period (Ij).
Learn more about equation from
https://brainly.com/question/29174899
#SPJ11
What is the slope of a line perpendicular to the line whose equation is x - 3y = -18. Fully reduce your answer.
Answers
Given:
Equation of a line is
\(x-3y=-18\)
To find:
The slope of the line perpendicular to the given line.
Solution:
The slope of the equation \(ax+by=c\) is
\(Slope=-\dfrac{a}{b}\)
We have,
\(x-3y=-18\)
Here, a=1, b=-3. So, slope of this line is
\(m_1=-\dfrac{1}{-3}\)
\(m_1=\dfrac{1}{3}\)
Product of slopes of two perpendicular lines is -1.
Let slope of perpendicular line is \(m_2\).
\(m_1\cdot m_2=-1\)
\(\dfrac{1}{3}\cdot m_2=-1\)
\(m_2=-3\)
Therefore, the slope of the perpendicular line is -3.
Write the equation of the line in standard form
y
5
3
2
1
X
1
4
2
5
3
-1
-5
-4
-3
-2
-2-
-3
Answers
Answer:
(5,1)
(3,4)
(2,2)
(1,5)
Solve the equation for the specified variable.
T= BA-9, for B
What does b=
Answers
9514 1404 393
Answer:
\(B=\dfrac{T+9}{A}\)
Step-by-step explanation:
Add 9 to both sides of the equation, and divide by the coefficient of B.
T = BA -9
T +9 = BA
(T +9)/A = B
We can rewrite that with B on the left:
B = (T +9)/A
find a power series for the function, centered at c. f(x) = 8 3x 2 , c = 5
Answers
The power series for the function\(f(x) = 8/(3x^2)\), centered at c = 5, is \(8/75 - 16/375(x-5) + 48/9375(x-5)^2 - 64/78125(x-5)^3 + ...\)
To find the power series for the function \(f(x) = 8/(3x^2)\)centered at c = 5, we can use the formula for the Maclaurin series:
\($f(x) = f(c) + \frac{f'(c)}{1!}(x-c) + \frac{f''(c)}{2!}(x-c)^2 + \frac{f'''(c)}{3!}(x-c)^3 + ...$\)
First, we need to find the derivatives of f(x):
\(f(x) = 8/(3x^2)\)
\(f'(x) = -16/(3x^3)\)
\(f''(x) = 48/(3x^4)\)
\(f'''(x) = -192/(3x^5)\)
Next, we evaluate these derivatives at c = 5:
\(f(5) = 8/(35^2) = 8/75\)
\(f'(5) = -16/(35^3) = -16/375\)
\(f''(5) = 48/(35^4) = 48/9375\)
\(f'''(5) = -192/(35^5) = -64/78125\)
Plugging these values into the formula, we get:
\(f(x) = 8/75 - 16/375(x-5) + 48/9375(x-5)^2 - 64/78125(x-5)^3 + ...\)
This is the power series for f(x) centered at c = 5.
Learn more about power series here:
https://brainly.com/question/14300219
#SPJ1
which is bigger 5.8 or 5.5
Answers
Answer:
5.8 is bigger
Step-by-step explanation:
Answer:
5.8
Step-by-step explanation:
Since they both start with 5, you look at the next number. Which ever number is bigger is the greater number.
Joannie lent $200 to her sister. 4 years later, her sister repaid her in full with $228. What simple annual interest rate did joannies sister pay?
Answers
Answer:
$7/year
Step-by-step explanation:
228-200 = 28
divide by the 4 years : 28/4= 7

