I need help solving this step by step. The second screenshot is an example that was given


Answers
Step-by-step explanation:
T→T = T
T→F = F
F→T = T
F→F = T
Related Questions
Graph the line of the equation x−2y=6 using its slope and y-intercept.
Answers
Step-by-step explanation:
take x and subtract it over to the other side you should get Negative two y equals negative x + 6 then divide it all by -2 and you should get y equals 1/2 x - 3

7) Solve the following systems of equations algebraically and check. 4x + 2y = 22 -2x + 2y = -8
Answers
The solution to the system of equation is as follows:
x = 5 and y = 1
How to solve system of equation?System of equation can be solved using different method such as elimination method and substitution method.
Therefore, let's solve the system of equation using elimination method as follows:
4x + 2y = 22
-2x + 2y = -8
subtract equation(ii) form equation(i)
6x = 30
divide both sides by 6
x = 30 / 6
x = 5
Hence, let's find the value of y
4x + 2y = 22
4(5) + 2y = 22
20 + 2y = 22
2y = 22 - 20
2y = 2
y = 2 / 2
y = 1
let's check whether or solution is correct.
-2(5) + 2(1) = -8
4(5) + 2(1) = 22
learn more on system of equation here: https://brainly.com/question/12287130
#SPJ1
Please help me please I will give brainliest!

Answers
Answer:
3) Because the run go by 4 and the rise go up by 2
Step-by-step explanation:
Vita wants to center a towel bar on her door that is 27 inches wide.
end of the door is 9 inches. Write and solve an equation to find the length
She determines that the distance from each end of the towel bar to the
of the towel bar.
Answers
The length of the towel bar is 9.5 inches.
How to solve the equation?Length is used to measure distance, In the International System of Quantities, a quantity with the distance dimension is referred to as length. The majority of measurement systems select a base unit for length from which all other units are derived. The metre serves as the International System of Units' fundamental unit of length.
Suppose, the length of the towel bar is x inches
The distance from each end of the towel bar to the end of the door is 9
inches. So, the total width of the door will be:[(x+(9*2)]=(x+18) inches
Given that, the width of the door is 27 inches 27.5 So, the equation will be.
x+18=27.5
x=27.5-18=9.5
Thus, the length of the towel bar will be 9.5 inches.
To learn more about length refers to;
brainly.com/question/9032191
#SPJ1
Fill in the blank to make equivalent rational expressions

Answers
Answer:
4
Step-by-step explanation:
Denominator is multiplied by -1, so the same with numerator.
WHAT IS 2/29 AS A DECIMAL
Answers
Answer:
0.068966
Step-by-step explanation:
Answer:
00.2 or 00.29 l guess sorry if it is wrong
WILL GIVE BRAINLIEST!!
What is the value of 1/60?

Answers
Answer:
1/6
Step-by-step explanation:
Answer:
C. 1
Step-by-step explanation:
Suppose 30% of the U.S. population has green eyes. If a random sample of size 1200 U.S. citizens is drawn, then the probability that less than 348 U.S. citizens have green eyes is _______.
Answers
Answer:
P(X is less than 348) = 0.2148
Step-by-step explanation:
Given that:
Sample proportion (p) = 0.3
Sample size = 1200
Let X be the random variable that obeys a binomial distribution. Then;
\(X \sim Bin(n = 1200,p =0.3)\)
The Binomial can be approximated to normal with:
\(\mu = np = 1200 \times 0.3 \\ \\ \mu= 360\)
\(\sigma = \sqrt{np(1-p) } \\ \\ \sigma = \sqrt{1200 \times (0.3)(1-0.3) } \\ \\ \sigma = 15.875\)
To find:
P(X< 348)
So far we are approximating a discrete Binomial distribution using the continuous normal distribution. 348 lies between 347.5 and 348.5
Normal distribution:
x = 347.5, \(\mu\) = 360, \(\sigma\) = 15.875
Using the z test statistics;
\(z = \dfrac{x - \mu}{\sigma}\)
\(z = \dfrac{347.5 - 360}{15.875}\)
\(z = \dfrac{-12.50}{15.875}\)
z = -0.7874
z ≅ - 0.79
The p-value for P(X<347.5) = P(Z < -0.79)
From the z tables;
P(X<347.5) = 0.2148
Thus;
P(X is less than 348) = 0.2148
Find the reciprocal of 7/12
Answers
Write 2 1/6
feet as a
single fraction greater than one.
Answers
Answer:
13/6
Step-by-step explanation:
2 x _/6 = 12/6, then add 1/6 and you have 13/6
25 people are interviewing and 9 people are getting accepted. what is the percentage for my chance of getting accepted?
Answers
Answer:
36%
Step-by-step explanation:
9/25 × 100% = 36%
Please mark me as brainliest
Answer:
36%
36%
Step by step explanation:
9/25 x 100% = 36%
What is the slope intercept equation for this line?

Answers
the slope for this line is 2
what is slope?The slope or gradient of a line is a number that describe both the direction and the steepness of the line. the steepness of a line is defined as the slope (or gradient). The slope is the ratio of vertical distance to the horizontal distance between any two points on a line. Mathematically, slope is calculated as "rise over run" (change in y divided by change in x).The greater the value of the slope, the "steeper" the slope is, and vice versa. So the smallest value of the absolute value of these slopes is 1/2.
So, A.T.Q:-
The formula of slopet intercept is Y2 -Y1 /X2-X1
From the question:
slope = -1-1/0-1
slope = 2
To know more about slope , click here;
https://brainly.com/question/28895146
#SPJ13
evaluate the expression for x=-3 Thank you
\( {x}^{2 } - 2x + 4\)
Answers
Answer: 7
Step-by-step explanation:
3 x 3 = 9 - 2(3)+4
9-6+4
=7
9
Look at the functions f (x) and g(x):
ƒ (x) = x²
g(x) = 2² +3
Which transformation of f (x) makes f(x) < g(x)?
Answers
The value of transformation of f (x) makes f(x) < g(x) is,
⇒ shifts the function 3 units upward.
We know that;
A transformation that occurs when a figure is moved from one location to another location without changing its size or shape is called translation.
Now, We have;
Functions are,
f (x) = x²
g(x) = x² +3
Hence, The value of transformation of f (x) makes f(x) < g(x) is,
⇒ shifts the function 3 units upward.
Learn more about the transformation visit:
https://brainly.com/question/30097107
#SPJ1
2
\( 2 \times 2\)
Answers
Answer:
4
Step-by-step explanation:
2 × 2 = 4
A wheel with radius 1 foot makes 1 revolution in 4 seconds. What is the linear velocity, in feet per second, of a point on the edge of the wheel? 4π 8π
Answers
Answer:
\(v=\dfrac{\pi}{2}\ ft/s\)
Step-by-step explanation:
Given that,
A wheel with radius 1 foot makes 1 revolution in 4 seconds
We need to find the linera velocity of a point on the edge of the wheel. We know that, the linear velcity is given by :
\(v=r\omega\)
Where
\(\omega\) is angular velcocity,\(\omega=2\pi\ rad\)
\(\omega=\dfrac{1}{4}\times 2\pi\\\\=0.5\pi\ rad/s\)
So
\(v=1\times 0.5\pi\\\\v=\dfrac{\pi}{2}\ ft/s\)
So, the linear velocity of the wheel is equal to \(\dfrac{\pi}{2}\ ft/s\).
Answer:
pi/2
B
Step-by-step explanation:
Got it right on EG
Enter the number that belongs in the green box
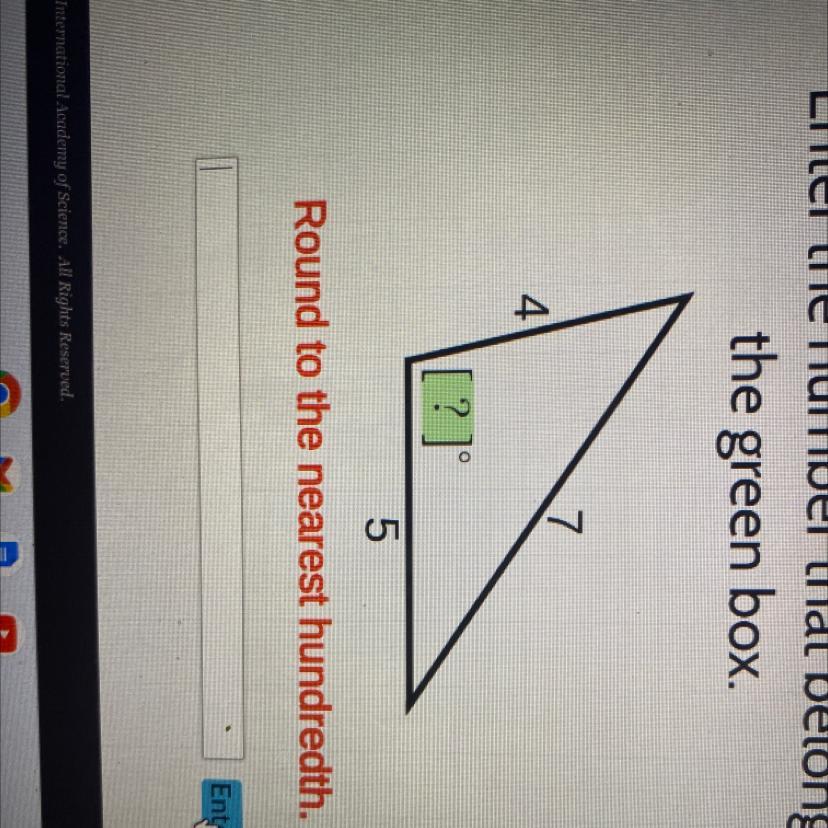
Answers
The angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
To find the measure of the angle between the sides measuring 4 and 5 in an obtuse triangle with side lengths 4, 5, and 7, we can use the Law of Cosines. The Law of Cosines states that in a triangle with side lengths a, b, and c, and an angle opposite to side c, the following equation holds:
\(c^2 = a^2 + b^2 - 2ab*cos(C)\)
In this case, we have side lengths a = 4, b = 5, and c = 7. We want to find the angle C, which is opposite to side c. Substituting these values into the Law of Cosines, we get:
\(7^2 = 4^2 + 5^2\)- 2(4)(5)*cos(C)
49 = 16 + 25 - 40*cos(C)
49 = 41 - 40*cos(C)
40*cos(C) = 41 - 49
40*cos(C) = -8
cos(C) = -8/40
cos(C) = -0.2
To find the measure of angle C, we can take the inverse cosine (arccos) of -0.2:
C = arccos(-0.2)
Using a calculator, we find that C ≈ 101.54 degrees.
Therefore, the measure of the angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
For more such information on: angle
https://brainly.com/question/25716982
#SPJ8
What's 5000 minus 3296
Answers
Answer:
1704
Step-by-step explanation:
Samuel can type nearly 40 words per minute. Use this information to find the number of hours it would take him to type 2.9 × 105 words.
Samuel can type 2.9 × 105 words in
hours and
minutes.
Answers
Answer:
Samuel can type 40 words per minute
Step-by-step explanation:.
Then how many hours will it take for him to type 2.6 words times 10 to the power of five words
=> 2.6 words time 10 to the power of 5
=> 2.6 x 10^5
=> 2.6 x 100 000
=> 260 000 words in all.
Now, we need to find the number of words Samuel can type in a hour
=> 40 words / minutes , in 1 hour there are 60 minutes
=> 40 x 60
=> 2 400 words /hour
Now, let’s divide the total of words he need to type to the number of words he can type in an hour
=> 260 000 / 2 400
=> 108.33 hours.
I don’t understand this?

Answers
Your answer is 11.5
Answer:
11.5 cm²
Step-by-step explanation:
We know that the triangle has a base of 3 + 4 = 7 and a height of 3 + 2 = 5. Therefore, the area of the triangle is 7 * 5 / 2 = 17.5. The area of the 3 by 2 rectangle is 3 * 2 = 6 so the shaded area is 17.5 - 6 = 11.5 square cm.
Post-Test
1
8. One brand of canned salmon is sold in four different sizes.
The 7-ounce can costs $3.49.
The 16-ounce can costs $6.49
The 24-ounce can costs $8.49. The 30-ounce can costs $10.99.
a. Calculate the unit rate (cost per ounce) for each size.
Answers
Answer:
See below.
Step-by-step explanation:
The 7-ounce can costs $3.49: ($3.49)/(7 oz) = $0.499/oz
The 16-ounce can costs $6.49: ($6.49)/(16 oz) = $0.406/oz
The 24-ounce can costs $8.49: ($8.49)/(24 oz) = $0.354/oz
The 30-ounce can costs $10.99: ($10.99)/(30 oz) = $0.366/oz
RSM a pharmisest has a 18 percent alcohol sulution and a 40 percent alcohol sulution how much of each must he use to make 10 leaters of 20 persent alcohol sulution
Answers
Answer:
To make 10 liters of 20% alcohol solution, RSM would need to use a combination of the 18% and 40% alcohol solutions. Let's call the amount of 18% solution used "x" and the amount of 40% solution used "y".
To set up the equation, we'll use the fact that the amount of pure alcohol in the final solution must be equal to 20% of the total volume.
So:
0.18x + 0.40y = 0.20(10)
Simplifying:
0.18x + 0.40y = 2
We have one equation with two unknowns, which means we need another equation. Fortunately, we know that RSM is making a total of 10 liters of solution. So:
x + y = 10
We now have two equations with two unknowns, which we can solve simultaneously. One way to do this is to solve one equation for one variable, then substitute that expression into the other equation, like so:
x = 10 - y (from the second equation)
0.18(10-y) + 0.40y = 2 (substituting into the first equation)
1.8 - 0.18y + 0.40y = 2
0.22y = 0.2
y = 0.91
So RSM would need to use approximately 0.91 liters (or 910 milliliters) of the 40% solution, and the rest (9.09 liters or 9090 milliliters) of the 18% solution, to make 10 liters of 20% alcohol solution.
. Suppose a government agency has a monopoly in the provision of internet connections.
The marginal cost of providing internet connections is 1
2
, whereas the inverse demand
function is given by: p = 1
Answers
The government agency as a monopolist will produce and sell internet connections up to the point where the marginal cost is 1/2. The price will be set at 1, given the perfectly elastic demand function.
In the scenario where a government agency has a monopoly in the provision of internet connections and the inverse demand function is given by p = 1, we can analyze the market equilibrium and the implications for pricing and quantity.
The inverse demand function, p = 1, implies that the market demand for internet connections is perfectly elastic, meaning consumers are willing to purchase any quantity of internet connections at a price of 1. As a monopolist, the government agency has control over the supply of internet connections and can set the price to maximize its profits.
To determine the optimal pricing and quantity, the monopolist needs to consider the marginal cost of providing internet connections. In this case, the marginal cost is given as 1/2. The monopolist will aim to maximize its profits by equating marginal cost with marginal revenue.
Since the inverse demand function is p = 1, the revenue received by the monopolist for each unit sold is also 1. Therefore, the marginal revenue is also 1. The monopolist will produce up to the point where marginal cost equals marginal revenue, which in this case is 1/2.
As a result, the monopolist will produce and sell internet connections up to the quantity where the marginal cost is 1/2. The monopolist will set the price at 1 since consumers are willing to pay that price.
For more such question on monopolist. visit :
https://brainly.com/question/28336090
#SPJ8
A baseball pitcher has made 53 pitches in the first four innings of a baseball game and plans to pitch 3 mote innings. The manager of the team has committed to allowing his pitcher to throw, at most, pitches during the game. Write an inequality to find the average number of pitches the pitcher can throw over the next three innings Solve the inequality from Part 1. What is the maximum number of pitches the pitcher can make in cach of the next 3 innings ? Graph your solution from Part 2 on a number line and explain what your solution means. If the pitcher threw just 6 pitches in the fifth inning, what is the greatest number of pitches the pitcher can throw per inning he wishes to pitch nine innings? Write and solve an inequality to answer this part.
Answers
Answer:
at most 17 pitches per inning
Step-by-step explanation:
It is given that a baseball pitcher makes 53 pitches in the first 4 innings of a game and plans to pitch in the next 3 innings.
We need to write and solve an inequality to find the possible average pitches per inning the pitcher made in the next 3 innings if the pitcher is assigned a maximum of 105 pitches.
From part (a) we know 3 p + 53 3p+53 represents the total number of pitches made if the pitcher makes an average of p pitches per inning in the next 3 innings.
If the pitcher can make at most 105 pitches, then:
3 p + 53 ≤ 105 3p+53≤105
To solve the inequality, first subtract 53 on both sides of the inequality to isolate the variable term:
3 p + 53 − 53 ≤ 105 − 53 3 p ≤ 53
3p+53≤105 \(p\leq 17\frac{1}{3}\)
at most 17 pitches per inning
(Hope this helps can I pls have brainlist (crown)☺️)
Linear sequence of 35/100,5/10,65/100
Answers
The linear rule for the sequence is f(n) = 7/20 + 3/20(n - 1)
Finding the linear rule for the sequenceFrom the question, we have the following parameters that can be used in our computation:
35/100,5/10,65/100
In the above sequence, we can see that 15/100 is added to the previous term to get the new term
This means that
First term, a = 35/100
Common difference, d = 15/100
The nth term is then represented as
f(n) = a + (n - 1) * d
Substitute the known values in the above equation, so, we have the following representation
f(n) = 35/100 + 15/100(n - 1)
So, we have
f(n) = 7/20 + 3/20(n - 1)
Hence, the explicit rule is f(n) = 7/20 + 3/20(n - 1)
Read more about sequence at
brainly.com/question/30499691
#SPJ1
NO LINKS!!! URGENT HELP PLEASE!!!!
Manny bought a brand new car in 2012 for $28,750. If the car depreciaites by 12% each year, write an exponential function to model the situation, then find how many years until the car is only worth $10,000
Answers
It will take approximately 8.53 years for the car to be worth $10,000, assuming a constant annual depreciation rate of 12%.
To model the depreciation of Manny's car, we can use the method for exponential decay:
\(y = a(1 - r)^t\)
Wherein:
y = the cost of the car at time ta = the initial value of the car (in 2012)r = the annual depreciation price (as a decimal)t = the time in yearsIn this situation, we've:
a = $28,750r = 12% = 0.12 (as a decimal)y = $10,000Substituting those values into the method, we get:
\($10,000 = $28,750(1 - 0.12)^t\)
Dividing each aspects by $28,750, we get:
\(0.3478 = (0.88)^t\)
Taking the logarithm of both facets (base 10), we get:
\(log(0.3478) = t*log(0.88)\)
Solving for t, we get:
\(t = log(0.3478)/log(0.88)\)
= 8.53 (rounded to two decimal locations)
Consequently, it'll take approximately 8.53 years for the car to be worth $10,000.
Learn more about exponential decay:-
https://brainly.com/question/30390038
#SPJ1
Answer:
8.26 years
Step-by-step explanation:
To model the depreciation of the car over time, we can use an exponential decay function in the form:
\(\large{\boxed{V(t) = V_0(1 - r)^t}\)
where:
V₀ is the initial value of the car.r is the depreciation rate per year (as a decimal).t is the time elapsed (in years)V(t) is the value of the car after t years.Given values:
V₀ = $28,750r = 12% = 0.12V(t) = $10,000Substitute these values into the formula and solve for t:
\(V(t) = V_0(1 - r)^t\)
\(10000=28750(1-0.12)^t\)
\(10000=28750(0.88)^t\)
\(\dfrac{10000}{28750}=(0.88)^t\)
\(\dfrac{8}{23}=(0.88)^t\)
\(\ln \left(\dfrac{8}{23}\right)=\ln (0.88)^t\)
\(\ln \left(\dfrac{8}{23}\right)=t\ln (0.88)\)
\(t=\dfrac{\ln \left(\dfrac{8}{23}\right)}{\ln (0.88)}\)
\(t=8.2611657...\)
Therefore, the car will be worth $10,000 after approximately 8.26 years, or about 8 years and 3 months.
Note: After 8 years, the car will be worth $10,339.49. After 9 years, the car will be worth $9,098.75. So the value of the car will reach $10,000 during the 9th year. Therefore, rounding up to 9 years may be more appropriate if the answer should be in whole years.
Read the question tell me if it’s hard for a 5 grader

Answers
Answer:
No, all you are doing is ordering them from least to greatest value. Your answer would be C.
Step-by-step explanation:
Answer:
danggg them fifth graders are gonna break there head
Step-by-step explanation:
A number decreased by 1/3 of itself
Answers
The answer is:
X-1/3x
Step-by-step explanation:
Since we do not know what number it is, we would say the number is x. 1/3 of itself is 1/3x so a number minus 1/3 of itself is X-1/3x
5 Practice
Question 10a
A rectangle is 18 feet long and 14 feet wide.
The area of the rectangle is
square feet.
The solution is
O Search
How do I solve this prob
Answers
Answer:
Given - A rectangle of length 18 feet and wide 14 feet
To find - Area
Solution -
Area of rectangle = Length * Breadth
=
\(18 \times 14\)
\(252\) square feet
Which of the following is a possibility for the degree of the function? Choose all that apply.

Answers
Answer:
"”45_56tffgffysuddeysrysyryrdudestyfsre8rsrudsrushdudyrusurrdu