I am still stuck on this basic math question. Rosa has 3 3/4 pounds of dough. She uses 1/8 of a pound for one roll. How many rolls could be made from Rosa's dough? I was told 30. But how did they get this answer?
Answers
Step-by-step explanation:
First convert the amount of dough into an improper fraction:
\(3\frac{3}{4}\:\text{lbs} = \dfrac{15}{4}\:\text{lbs}\)
Each roll is 1/8 lb so divide the amount of dough by this amount:
\(\dfrac{\left(\dfrac{15}{4}\:\text{lbs}\right)}{\left(\frac{1}{8}\:\text{lb/roll}\right)} = \left(\dfrac{15}{4}\:\text{lbs}\right)\cdot \left(8\:\dfrac{\text{roll}}{\text{lb}}\right) = 30\:\text{rolls}\)
Related Questions
Given the graph of y = f(x) shown below, sketch the graph of y = |f(x)|.





Answers
Answer:
Graph C
Step-by-step explanation:
The graph of |f(x)| represents the absolute value of the function f(x).
The absolute value function removes the negative sign from any negative values, so it reflects the negative portion of the graph of f(x) across the x-axis.
Therefore, the correct graph is option C (attached).
Additional notes
Graph B is the function reflected across the x-axis: -f(x).
Graph D is the absolute function reflected across the x-axis: -|f(x)|.

what is.
m + 0.6 = 2.6
Answers
Answer:
m is 2 because 2.6 - 0.6 = 2 . so 2 is the answer
An architect is designing square windows with an area of(x2 + 16x +64) ft?. The dimensions of the
windows are of the form ax +b, where a and b are whole numbers.
Part 1 out of 2
Find an expression for the perimeter of the windows.
The perimeter of the square is represented by
(x+
6 ft.
Answers
A) The dimensions are (x+10) by (x+10).
B) The perimeter is given by 4x+40.
C) The perimeter when x is 4 is 56.
The quadratic can be factored by finding factors of c, the constant, that sum to b, the coefficient of x. Our c is 100 and our b is 20; we want factors of 100 that sum to 20. 10*10=100 and 10+10=20, so those are what we need. This gives us (x+10)(x+10 for the factored form.
Since the dimensions are all (x+10), and there are 4 sides, the perimeter is given by 4(x+10). Using the distributive property we have 4*x+4*10=4x+40.
To find the perimeter when x=4, substitute 4 into our perimeter expression:
4*4+40=16+40=56.
Answer:
A) The dimensions are (x+10) by (x+10).
B) The perimeter is given by 4x+40.
C) The perimeter when x is 4 is 56.
Step-by-step explanation:
I filled two notebook papers to solve this
stered comsident p43336280840
Save the expression by solating the variable Hemember to balance the equation in each step you take
2
0-6
Answers
The result of the expression 20 - 6 is 14.
To solve the given expression, 20 - 6, and isolate the variable, we need to clarify whether there is an equation involved. However, in this case, the expression does not contain any variable to isolate, and it is not an equation that needs balancing. It is a straightforward arithmetic expression.
Step 1: Start with the given expression, 20 - 6.
Step 2: Evaluate the subtraction operation: 20 - 6 = 14.
Step 3: The simplified expression is now 14. However, since there is no variable present, there is no need to isolate any variable.
This means that when you subtract 6 from 20, the answer is 14. Remember that isolating a variable and balancing an equation are relevant when dealing with equations that involve variables. In this case, the expression is a simple subtraction operation, yielding a constant value of 14 as the answer.
For more questions on Arithmetic expression
https://brainly.com/question/29525069
#SPJ8
solve for the unknown angle measure given that f || g

Answers
The measure of the unknown angle is 75°
What is an angle?
An angle is a shape in Euclidean space created by two rays, termed the ends of the angle, that share a common termination, called the vertex of the angle. Angles produced by two rays are located in the longitudinal plane the rays. Angles are also generated when two planes overlap. These are known as dihedral angles. An angle defined by two intersecting curves is the angle of the rays lying tangent to the respective curves at their point of junction. Angle can also refer to the measurement of an angle or of a rotation. In the case of a geometric angle, the arc is defined by the sides and is centered at the vertex.
From figure,
x+70+25 = 180 (angle sum property of a triangle)
x = 180 - 95 = 75°
Hence, the measure of the unknown angle is 75°
To know more about angles, click on the link
https://brainly.com/question/2399464
#SPJ13
I am in desperate need of help!!7. D is the midpoint of CE Prove: D=1/2CE

Answers
just follow the steps given in the question
determine if the statement is true of false. a fourth degree polynomial has exactly two relative minima and two relative maxima
Answers
Answer: True
Step-by-step explanation:
Translate the given phrase into an algebraic expression and simplify if possible: the sum of -4 and the difference of 3 and 1
Answers
Algebraic expression for the given phrase is
\(-4+(3-1)\)
Simplified answer is -2
Given :
The given phrase is the sum of -4 and the difference of 3 and 1
To find the difference we subtract the numbers
difference of 3 and 1 is 3-1
for the sum we add it
the sum of -4 and the difference of 3 and 1
the sum of -4 and (3-1)
Now we add it , \(-4+(3-1)\)
Algebraic expression for the given phrase is
\(-4+(3-1)\)
Now we simplify it
\(-4+(3-1)\\-4+(2)\\-2\)
Learn more : brainly.com/question/24513204
5.6.8 let f be a uniformly continuous function on a set e. show that if {xn} is a cauchy sequence in e then {f(xn)} is a cauchy sequence in f(e). show that this need not be true if f is continuous but not uniformly continuous.
Proof. (1): To prove {f(xn)} is a Cauchy sequence just need to prove ∀ > 0, ∃N, s.t.,∀n, m > N,
have |f(xn) − f(xm)| < . Since f is uniformly continuous on set E, thus ∀ > 0, ∃δ > 0, s.t.,
∀x, y ∈ E, if |x − y| < δ,then |f(x) − f(y)| < .as {xn} is a Cauchy sequence, then ∃N, s.t.,
∀n, m > N, |xn − xm| < δ, thus |f(xn) − f(xm)| < which proves {f(xn)} is a Cauchy sequence.
(2): for example f(x) = 1
x
, x ∈ (0, 2) which is continuous but not uniformly continuous. {
1
n
} is
a Cauchy sequence, however, {f(xn)} does not converge which proves that it is not a Cauchy
sequence.
Answers
Showing that this need not be true if f is continuous but not uniformly continuous.
Given :
let f be a uniformly continuous function on a set e. show that if {xn} is a cauchy sequence in e then {f(xn)} is a cauchy sequence in f(e).
( 1 )
If f is uniformly continuous on E, then given ε > 0 there is δ > 0 such that if x, y are in E and |x−y| < δ,
then |f(x) − f(y)| < ε. Let (xn) be a Cauchy sequence in E. Then given δ > 0 there is N such that if p, q > N,
then |xp − xq| < δ, and thus |f(xp) − f(xq)| < ε, implying that (f(xn)) is a Cauchy sequence.
( 2 )
Let E = {1, 1/2, 1/3, · · } and f(1/n) = 1 is n is odd, f(1/n) = −1 if
n is even. Then f is continuous but not uniformly continuous. The sequence (xn) = (1/n) in E is Cauchy but the
sequence (f(xn)) = (1, −1, 1, −1, · · ·) is not Cauchy.
Learn more about the sequence here:
https://brainly.com/question/21961097
#SPJ4
Naomi's dining room is 7 yards wide and 7 yards long. Naomi wants to install wooden trim around the top of the room. The trim costs $9.00 per yard. How much will it cost Naomi to buy enough trim?
Answers
Please help due in a few minutes

Answers
Answer:
B? I think its b. Im not completely sure tho
Step-by-step explanation:
The volume of square pyramid is 25 cubic inches. You want the height to be 2 inches less than the edge of the base. What are the dimensions?
Answers
Step-by-step explanation:
Find several points that are on the graph of the function y = x^2 + 1. Plot the points in a coordinate plane.
Is this a linear function? Explain.

Answers
Answer:
Below.
Step-by-step explanation:
Plot following points.
Calculate the point by plugging in values of x into x^2 + 1
for example When x = 0, y = 0^1 + 1 = 1.
So plot plot (0, 1),
Make a table of points to plot:
x -3 -2 -1 0 1 2 3
y 10 5 2 1 2 5 10
When you plot the points you'll see the graph is U shaped.
The function is of second degree (as it contains x^2) so it wont be linear.
the double number line shows that 4 bottles of water cost 10 dollars at a music festival
Answers
Answer:
That means that each water is $2.50, das crazy tho
Step-by-step explanation:
What is the equation of the line in slope intercept form?

Answers
Answer:
y = x + 60
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
calculate m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (20, 80) and (x₂, y₂ ) = (40, 100) ← 2 points on the line
m = \(\frac{100-80}{40-20}\) = \(\frac{20}{20}\) = 1
the line crosses the y- axis at (0, 60 ) ⇒ c = 60
y = x + 60 ← equation of line
Find the area of the shaded region. The graph to the right depicts IQ scores of adults, and those scores are normally distributed with a mean of 100 and a standard deviation of 15.
Click to view page 1 of the table. LOADING... Click to view page 2 of the table. LOADING...
115
A graph with a bell-shaped curve, divided into 2 regions by a vertical line. The vertical line extends from the bell curve to the x-axis, and is located on the right half, under the curve. The region on the left of this line is shaded. The x-axis below the vertical line is labeled 115.
Question content area bottom
Part 1
The area of the shaded region is enter your response here. (Round to four decimal places as needed.)

Answers
The area of the given shaded region is 0.1587 which can be calculated using the cumulative area of the normal distribution.
What is z-score?The z-score is the number of standard deviations a data point is away from the mean. It can be calculated by subtracting the mean from the data point, and then dividing by the standard deviation.
To calculate the area of the shaded region, the z-score for the value of 115 must first be determined.
In this case, the z-score= (115 - 100)/15, or 1.
The area of the shaded region is then calculated using the cumulative area of the normal distribution.
As the area of the shaded region is the probability of a data point being greater than 115, the cumulative area of the normal distribution should be subtracted from 1 to get the area of the shaded region.
The cumulative area of the normal distribution for a z-score of 1= 0.8413,
as z-score= x - μ/σ
so the area of the shaded region
=1 - 0.8413
= 0.1587.
For more questions related to standard deviation
https://brainly.com/question/24298037
#SPJ1
Answer this question pls I need it rn
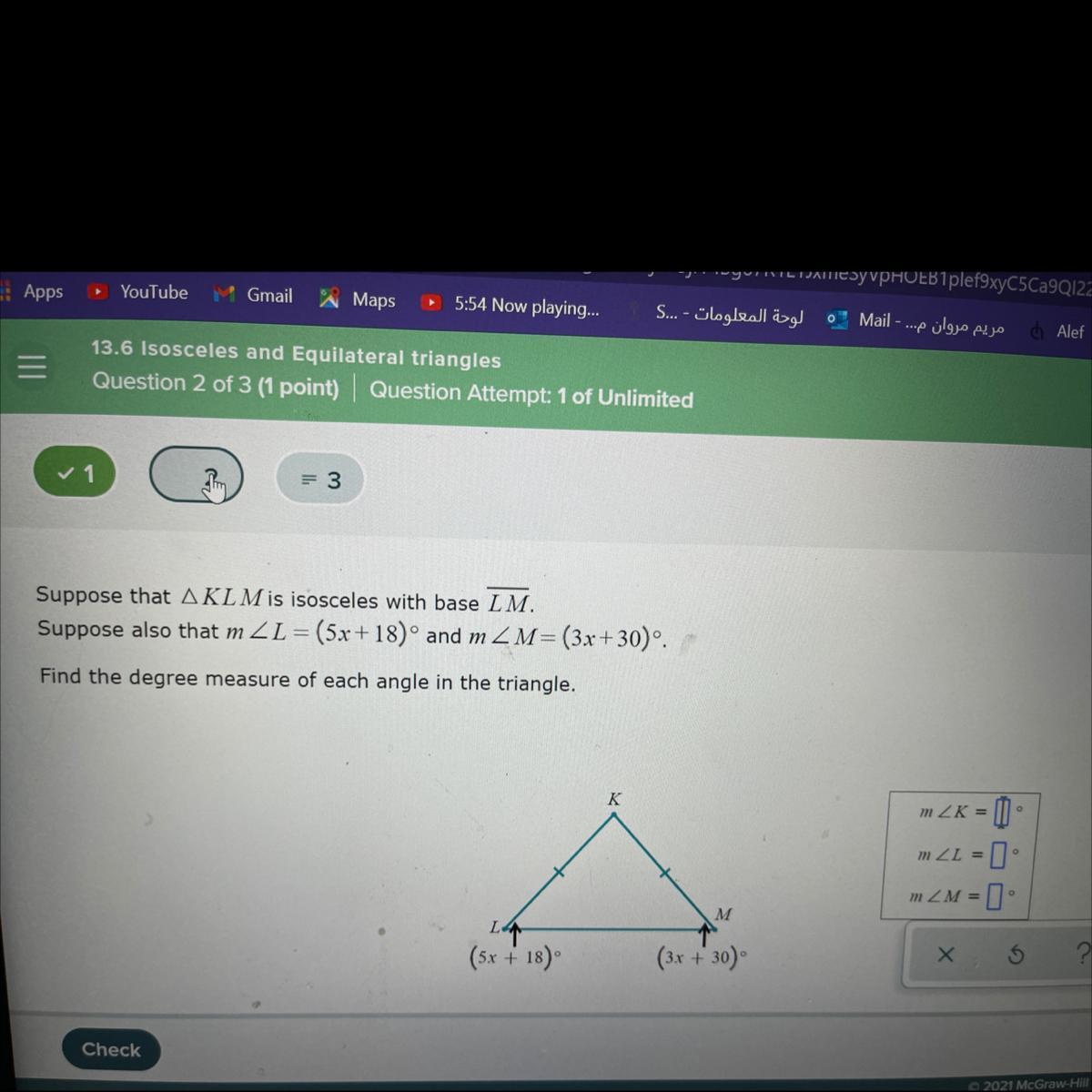
Answers
Answer:
K = 84°
L ; M = 48 ; 48
Step-by-step explanation:
L = (5x + 18)
M = (3x + 30)
K = k
L + M + K = 180° (sum of angles in a triangle)
The two base angles are equal :
Hence ;
5x + 18 = 3x + 30
5x - 3x = 30 - 18
2x = 12
x = 6
Hence,
L = 5x + 18 = 5(6) + 18 = 30 + 18 = 48°
M = 3x + 30 = 3(6) + 30 = 48°
K = 180 - (48 + 48)
K = 180 - 96
K = 84°
Solve the equation: x²-2x=8
Show all the Steps with explanation.
Answers
Answer:
x = 4, -2
Step-by-step explanation:
x^2-2x=8
Move the constant term to the right side of the equation.
x^2 - 2x = 8
Take half of the coefficient of x and square it.
(-2/2)^2 = 1
Add the square to both sides of the equation.
x^2 - 2x + 1 = 8 + 1
Factor the perfect square trinomial.
(x - 1)^2 = 9
Take the square root of both sides of the equation.
x-1=\(\sqrt{9}\)
x-1=±3
Isolate x to find the solutions.
Taking positive
x=3+1=4
x=4
Taking negative
x=-3+1
x=-2
The solutions are:
x = 4, -2
Answer:
\(x = -2,\;\;x=4\)
Step-by-step explanation:
To solve the quadratic equation x² - 2x = 8 by factoring, subtract 8 from both sides of the equation so that it is in the form ax² + bx + c = 0:
\(x^2-2x-8=8-8\)
\(x^2-2x-8=0\)
Find two numbers whose product is equal to the product of the coefficient of the x²-term and the constant term, and whose sum is equal to the coefficient of the x-term.
The two numbers whose product is -8 and sum is -2 are -4 and 2.
Rewrite the coefficient of the middle term as the sum of these two numbers:
\(x^2-4x+2x-8=0\)
Factor the first two terms and the last two terms separately:
\(x(x-4)+2(x-4)=0\)
Factor out the common term (x - 4):
\((x+2)(x-4)=0\)
Apply the zero-product property:
\(x+2=0 \implies x=-2\)
\(x-4=0 \implies x=4\)
Therefore, the solutions to the given quadratic equation are:
\(\boxed{x = -2,\;\;x=4}\)
x+5+4-5=x+54
Help !!!
Answers
=>x+5+4−5=x+54
=>x+5+4+−5=x+54
=>(x)+(5+4+−5)=x+54(Combine Like Terms)
=>x+4=x+54
=>x+4=x+54
Subtract x from both sides=>x+4−x=x+54−x
=>4=54
Subtract 4 from both sides=>4−4=54−4
=>0=50
There are no solutionsun cono mide 3 pulgadas de diámetro. a este cono le caben 12 pulgadas cúbicas de agua. redondeada a la pulgada más cercana. ¿ cuál es la altura del cono?
Answers
jasmine
was the lead dancer for her dance troupe. She and the troupe's choreographer (also a troupe member) decided that they needed to have one more rehearsal before they performed.
Answers
The members in Jasmine's dance troupe is an illustration equivalent expressions.
The number of members in Jasmine's dance troupe is 62
Assume the number of dancers is n.
One third of the rest is:
\(\mathbf{x = \frac{1}{3}(n - 2)}\)
When she called three more, we have:
\(\mathbf{x = \frac{1}{3}(n - 2) + 3}\)
Expand
\(\mathbf{x = \frac{n}{3} - \frac{2}{3} + 3}\)
\(\mathbf{x = \frac{n}{3} + \frac{-2 + 9}{3}}\)
\(\mathbf{x = \frac{n}{3} + \frac{7}{3}}\)
The remaining dancers (r) are:
\(\mathbf{r = n- \frac{n}{3} - \frac{7}{3}}\)
\(\mathbf{r = \frac{3n - n}{3} - \frac{7}{3}}\)
\(\mathbf{r = \frac{2n}{3} - \frac{7}{3}}\)
\(\mathbf{r = \frac{2n - 7}{3}}\)
When two-fifth of the remaining dancers are added, we have:
\(\mathbf{x = \frac{n}{3} + \frac{7}{3} + \frac{2}{5}(\frac{2n - 7}{3})}\)
\(\mathbf{x = \frac{n+7}{3} + \frac{2}{5}(\frac{2n - 7}{3})}\)
\(\mathbf{x = \frac{n+7}{3} + \frac{4n - 14}{15}}\)
Take LCM
\(\mathbf{x = \frac{5n + 35 + 4n - 14}{15}}\)
\(\mathbf{x = \frac{9n + 21}{15}}\)
\(\mathbf{x = \frac{3n + 7}{5}}\)
When she called one more dancer, we have:
\(\mathbf{x = \frac{3n + 7}{5} + 1}\)
\(\mathbf{x = \frac{3n + 7+5}{5}}\)
\(\mathbf{x = \frac{3n + 12}{5}}\)
The remaining of the dancer is:
\(\mathbf{r = n - \frac{3n + 12}{5}}\)
\(\mathbf{r = \frac{5n - 3n + 12}{5}}\)
\(\mathbf{r = \frac{2n + 12}{5}}\)
When three-fourth are added, we have:
\(\mathbf{x = \frac{3n + 12}{5} +\frac{3}{4} \times \frac{2n + 12}{5}}\)
\(\mathbf{x = \frac{3n + 12}{5} + \frac{6n + 36}{20}}\)
Take LCM
\(\mathbf{x = \frac{12n + 48+6n + 36}{20}}\)
\(\mathbf{x = \frac{18n +84}{20}}\)
When the last two members are added, we have:
\(\mathbf{n = \frac{18n +84}{20} + 2}\)
\(\mathbf{n = \frac{18n +84+40}{20} }\)
\(\mathbf{n = \frac{18n +124}{20} }\)
Multiply through by 20
\(\mathbf{20n = 18n +124}\)
Collect like terms
\(\mathbf{20n - 18n =124}\)
\(\mathbf{2n =124}\\\)
Divide both sides by 2
\(\mathbf{n =62}\)
Hence, the number of members in Jasmine's dance troupe is 62
Read more about equivalent expressions at:
https://brainly.com/question/15715866
A Norman window is constructed by adjoining a semicircle to the top of an ordinary rectangular window. What is the maximum area of a Norman window whose perimeter is 9 feet?
Answers
The maximum area of a Norman window with a perimeter of 9 feet is 81π/4 square feet.
To find the maximum area of a Norman window with a given perimeter, we can use calculus. Let's denote the radius of the semicircle as r and the height of the rectangular window as h.The perimeter of the Norman window consists of the circumference of the semicircle and the sum of all four sides of the rectangular window. Therefore, we have the equation:
πr + 2h = 9We also know that the area of the Norman window is the sum of the area of the semicircle and the area of the rectangle, given by:
A = (πr^2)/2 + rh
To find the maximum area, we need to express the area function A in terms of a single variable. We can do this by substituting r from the perimeter equation:
r = (9 - 2h)/(π)
Now we can rewrite the area function in terms of h only:
A = (π/2) * ((9 - 2h)/(π))^2 + h * (9 - 2h)/(π)
Simplifying this equation, we get:
A = (1/2)(9h - h^2/π)
To find the maximum area, we differentiate the area function with respect to h, set it equal to zero, and solve for h:
dA/dh = 9/2 - h/π = 0
Solving this equation, we find:h = 9π/2
Substituting this value of h back into the area function, we get:
A = (1/2)(9 * 9π/2 - (9π/2)^2/π) = (81π/2 - 81π/4) = 81π/4
Therefore, the maximum area of a Norman window with a perimeter of 9 feet is 81π/4 square feet.
Learn more about area here:
https://brainly.com/question/2607596
#SPJ8
Is 3/4 greater than 3/5

Answers
Answer:
Yes.
Explanation:
3/4 is 75% of a whole, 3/5 is 60%.
Calculate the value of each expression.
−18/3
please help i cant find it!
Answers
Answer:
-6
Step-by-step explanation:
Please help. The best way to explain is to say, This value goes in this box.

Answers
Answer:
The last one is 6/9.
Step-by-step explanation:
Hope that helps
Correct answer gets brainliest

Answers
The correct option is (d) i.e. The area of the given parallelogram will be 36 ft²
What is a Parallelogram ?
A quadrilateral with two sets of parallel sides is known as a parallelogram. A parallelogram has equal-sized opposite sides and opposite angles. Additionally, the interior angles on the same side of the transversal are additional. 360 degrees is the total of all interior angles.
The term "parallelepiped" refers to a three-dimensional shape with parallelogram-shaped faces. The base (one of the parallel sides) and height (the distance from top to bottom) of a parallelogram determine its area, respectively. The length of each of a parallelogram's four sides determines its perimeter.
Given : base of parallelogram = 4+2= 6 ft
height of the parallelogram = 6ft
We know that, area of a parallelogram = base × height
So, Area of the given parallelogram = 6 × 6
= 36 ft²
Hence, The correct option is (d).
To learn more about Parallelogram, visit the link:
https://brainly.com/question/20526916
#SPJ1
ng a sentence into a one-step equationTranslate this sentence into an equation.The sum of 17 and Carlos's height is 43.Use the variable c to represent Carlos's height.=O+ローロロメロX$?

Answers
C + 17 = 43
STEP - BY - STEP EXPLANATION
What to find?
The height of Carlos.
Given:
The sum of 17 and Carlos's height is 43.
To solve, we will follow the step below:
Step 1
Translate the key word into an equation.
That is;
"sum" means +
Step 2
Translate the whole of the sentence into one - step equation.
Let C be Carlos' height.
C + 17 = 43
Therefore, the one step equation is C + 17 = 43
Solve 2-3 cos x=5+3 cosx for 0° ≤ 180°
Answers
The equation 2-3cos(x) = 5+3cos(x) has no solution in the range of 0° to 180°.
1. Start with the given equation: 2-3cos(x) = 5+3cos(x).
2. Subtract 3cos(x) from both sides to isolate the constant term: 2-3cos(x) - 3cos(x) = 5.
3. Combine like terms: 2-6cos(x) = 5.
4. Subtract 2 from both sides: -6cos(x) = 3.
5. Divide both sides by -6: cos(x) = -1/2.
6. To find the solutions for cos(x) = -1/2 in the range of 0° to 180°, we need to determine the angles where cos(x) equals -1/2.
7. These angles are 120° and 240°, as cos(120°) = cos(240°) = -1/2.
8. However, the given equation states that 2-3cos(x) equals 5+3cos(x), which is not satisfied by cos(x) = -1/2.
9. Therefore, the equation 2-3cos(x) = 5+3cos(x) has no solution in the range of 0° to 180°.
For more such questions on equation, click on:
https://brainly.com/question/17145398
#SPJ8
A ball is thrown downward from the top of a 150-foot building with an initial velocity of 23 feet per second. The height of the ball h after t seconds is given by the equation h= - 16t? - 23t+150. How long after the ball is thrown will it strike the ground?
Answers
Answer:
362 the answer
Step-by-step explanation:
follow nmn i hope its help
A large jet uses 7.500 gallons of fuel to fly 1,500 miles what is the unit rate used by the vehicle
Answers
We know that they are using 7500 gallons of fuel for 1500 miles
we can do 7500 / 1500 = 5
Meaning that for every 5 gallons of fuel they travel 1 mile