hi pls answer this one...\
ii) 6 taps with the same rate of flow can fill a tank in 18 minutes. If two taps are closed, how long will the remaining taps take to fill the tank?
Answers
Answer:
I think it is 12 minutes.
Answer:
Given that,
8 taps of the same size fill a tank in 27 minutes.
So, 1 tap can fill the tank in 7×27=189 minutes
If two taps go out of order, then the remaining taps =7−2=5
Therefore, Time taken by 6 taps to fill the tank =6÷289=0.0264550265
Related Questions
In ideal projectile motion, when the positive -axis is chosen to be vertically upward, the -component of the velocity of the object during the ascending part of the motion and the -component of the velocity during the descending part of the motion are, respectively, a) positive, negative. b) negative, positive. c) positive, positive. d) negative, negative.
Answers
In ideal projectile motion, when the positive -axis is chosen to be vertically upward, the -component of the velocity of the object during the ascending part of the motion and the -component of the velocity during the descending part of the motion are b) negative, positive respectively.
In ideal projectile motion, the initial velocity of an object can be separated into its x-component (horizontal) and y-component (vertical). When the positive y-axis is chosen to be vertically upward, the object experiences a constant acceleration due to gravity.
This results in a negative y-component of velocity during the ascending part of the motion (as the object is moving upwards against gravity) and a positive y-component during the descending part of the motion (as the object is falling downwards with gravity).
To summarize, the y-component of velocity is negative during the ascending part of the motion and positive during the descending part. This is because gravity acts downwards, causing the object to slow down as it rises and speed up as it falls.
For more questions like Projectile motion click the link below:
https://brainly.com/question/30034780
#SPJ4
pls i'll give brainliest answer these four for brainliest




Answers
Answer:
294 teenagers
Step-by-step explanation:
31.5$
102ml
50 hamburgers
Step 1: Our output value is 700.
Step 2: We represent the unknown value with $x$x.
Step 3: From step 1 above,$700=100\%$700=100%.
Step 4: Similarly, $x=42\%$x=42%.
Step 5: This results in a pair of simple equations:
$700=100\%(1)$700=100%(1).
$x=42\%(2)$x=42%(2).
Step 6: By dividing equation 1 by equation 2 and noting that both the RHS (right hand side) of both
equations have the same unit (%); we have
$\frac{700}{x}=\frac{100\%}{42\%}$
700
x=
100%
42%
Step 7: Again, the reciprocal of both sides gives
$\frac{x}{700}=\frac{42}{100}$
x
700=
42
100
Therefore, 42% of 700 is 294.
What is the slope of this graph?
Responses

Answers
Answer:
slope = -4
Step-by-step explanation:
A (-2,5)
B (0, -3)
slope = (-3-5)/(0-(-2)
-8/2
-4
Jana divided a sheet of paper into 5 equal sections and colored 2 of the sections red. What precent of the paper did she color ( ik the answer is ez my mom told me to think, but im too lazy to think )
Answers
Answer:
are u dumxb?? asur grandpa in the graveyard
PLEASE HELP I WILL GIVE BRAINLIEST FOR THE CORRECT ANSWER!!
Use mathematical induction to prove that 1 + 2 + 3 + … + n = (1/2) n (a1 + an).
Use the result to find the sum of 1 + 2 + 3 + ... + 500.
Answers
Answer:
See below for proof.
\(S_{500}=125250\)
Step-by-step explanation:
Given arithmetic series:
1 + 2 + 3 + … + nTherefore:
\(S_n=1+2+3+...+(n-2)+(n-1)+n\)
\(S_n=1+(1+1)+(1+2)+...+(1+n-3)+(1+n-2)+(1+n-1)\)
\(S_n=1+(1+1)+(1+2(1))+...+(1+(n-3)(1))+(1+(n-2)(1))+(1+(n-1)(1))\)
Let:
a = first term = 1d = common difference = 1n = nth termTherefore:
\(S_n=a+(a+d)+(a+2d)+...+(a+(n-3)d)+(a+(n-2)d)+(a+(n-1)d)\)
Reverse the order:
\(S_n=(a+(n-1)d)+(a+(n-2)d)+(a+(n-3)d)+...+(a+2d)+(a+d)+a\)
Add the two expressions for Sₙ:
\(2S_n=(2a+(n-1)d)+(2a+(n-1)d)+(2a+(n-1)d)+...+(2a+(n-1)d)\)
Therefore, the term (2a + (n – 1)d) has been repeated n times:
\(2S_n=n(2a+(n-1)d)\)
Divide both sides by 2:
\(S_n=\dfrac{1}{2}n(2a+(n-1)d)\)
\(S_n=\dfrac{1}{2}n(a+a+(n-1)d)\)
Replace a with a₁ (first term) and a + (n – 1)d with aₙ (last term):
\(S_n=\dfrac{1}{2}n(a_1+a_n)\)
To find the sum of the series 1 + 2 + 3 + ... + 500, substitute the following values into the formula:
a₁ = 1aₙ = 500n = 500Therefore:
\(\implies S_{500}=\dfrac{1}{2}(500)(1+500)\)
\(\implies S_{500}=250(501)\)
\(\implies S_{500}=125250\)
Work out an expression, in terms of x, for the perimeter of the shape.
Simplify your answer.
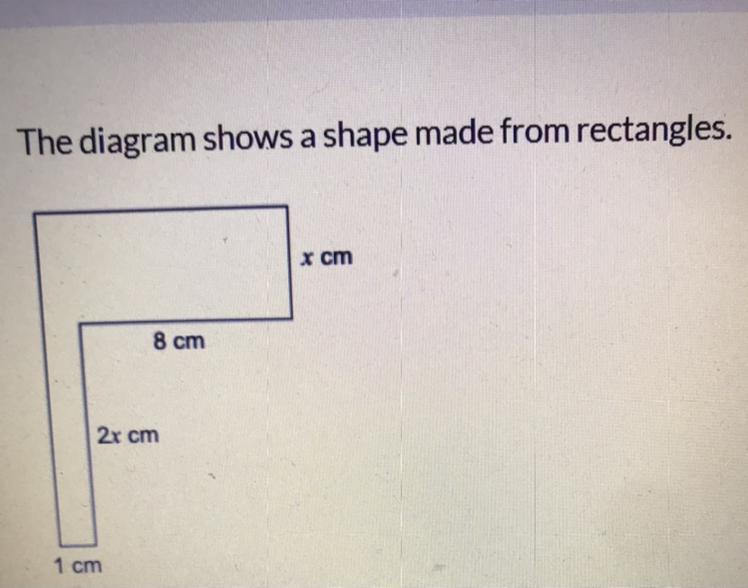
Answers
Answer:1+3x+9+x+8+2x= 6x+9
so =3(x+3)
Step-by-step explanation:
Cal has spent 35 on baseball cards. If he spent 12. 50 on a set of baseball cards each week,in how many weeks will cal have spent more then 500
Answers
Cal will have spent more than $500 after 28 weeks.
We can start by setting up an equation to represent Cal's spending on baseball cards:
Total spending = 12.50 * number of weeks
We can then use this equation to find out in how many weeks Cal will have spent more than $500:
12.50 * number of weeks > 500
Dividing both sides by 12.50, we get:
number of weeks > 500 / 12.50
number of weeks > 40
So, Cal will have spent more than $500 after 40 weeks. However, the question asks for the number of weeks after which Cal will have spent more than $500, given that he has already spent $35.
To find the number of weeks after which Cal will have spent more than $500, we need to subtract the amount he has already spent from $500:
$500 - $35 = $465
Now we can use the original equation to find the number of weeks:
12.50 * number of weeks = $465
Dividing both sides by 12.50, we get:
number of weeks = $465 / 12.50
number of weeks = 37.2
Since we can't have a fraction of a week, we need to round up to the nearest whole number. Therefore, Cal will have spent more than $500 after 38 weeks.
However, we need to remember that Cal has already spent $35, so we need to subtract that from the total amount he will have spent:
$500 - $35 = $465
$465 / 12.50 = 37.2
37.2 + 1 = 38
Therefore, Cal will have spent more than $500 after 38 weeks or 28 weeks from now.
Learn more about Equations:
https://brainly.com/question/2972832
#SPJ4
Which graph represents the function f(x)= √x-2?
Answers
Answer:
x y
0 -2
1 -1
2 -0.56
Step-by-step explanation:
given m||n, find the value of x

Answers
Answer:
Step-by-step explanation:
The value of x is 19 if the lines l and m are parallel.
The lines l and m are parallel
The corresponding angles are equal
We have to find the value of x
6x-9 = 5x+10
Let us take all the variable terms on one side
6x-5x=10+9
x=19
Hence, the value of x is 19 if the lines l and m are parallel.
To learn more on Coordinate Geometry click:
brainly.com/question/27326241
#SPJ1
(6x -7) +(-4x - 8) simplified
Answers
Answer:
2x−15
Step-by-step explanation:
6x−7−4x−8
=6x+−7+−4x+−8
Combine Like Terms:
=6x+−7+−4x+−8
=(6x+−4x)+(−7+−8)
=2x+−15
If the following triangles are similar solve for x

Answers
Answer:
x = 16
Step-by-step explanation:
Given that ∆EFG ~ ∆ABC, therefore the ratio of the their corresponding sides would be equal.
Thus:
EG/AC = EF/AB
EG = 756
AC = (45x - 76)
EF = 1107
AB = 943
Plug in the values into the equation
756/(45x - 76) = 1107/943
Cross Multiply
756*943 = (45x - 76)*1107
712,908 = 49,815x - 84,132
712,908 + 84,132 = 49,815x
797,040 = 49,815x
797,040/49,815 = x
16 = x
x = 16
Please help..........

Answers
Answer:
4 3/4
Step-by-step explanation:
a survey found that 78% of the men questioned preferred computer-assisted instruction to lecture and 68% of the women preferred computer-assisted instruction to lecture. there were 100 randomly selected individuals in each sample. find the 95% confidence interval for the difference of the two proportions.
Answers
The 95% confidence interval for the difference between the two population proportions is -0.022 < p₁ - p₂ < 0.222.
Given that,
In a survey, it was discovered that 68% of women and 78% of men preferred computer-assisted education to lectures, respectively. Each sample contained 100 people that were chosen at random.
We have to calculate the 95% confidence range for the difference between the two proportions.
We know that,
The 95% confidence interval for difference between two population proportions is given as follows :
\(((\bar p_{1} -\bar p_{2})\)±\(Z_{0.05/2}\sqrt{\frac{PQ}{n_{1} } +\frac{PQ}{n_{2} }} })\)
Here,
p₁ is 0.78
p₂ is 0.68
n₁ is 100
n₂ is 100
Z is 1.96
P is 0.73
Q is 0.27
So,
((0.78-0.68)±\(1.96\sqrt{\frac{(0.73)(0.27)}{100 } +\frac{(0.73)(0.27)}{100 }} })\)
(0.10±0.122)
(0.10-0.122,0.10+0.122)
(-0.022,0.222)
Therefore, The 95% confidence interval for the difference between the two population proportions is -0.022 < p₁ - p₂ < 0.222.
To learn more about interval visit: https://brainly.com/question/10850002
#SPJ4
reflect coordinates A(0,1) B(2,-4) C(-2,-4) over the y-axis, what is the new coordinates for points A' B' and C' ?
Answers
Answer:
- 18369919
Step-by-step explanation:
Hope that helps!
can someone please help me

Answers
Answer:
800
Step-by-step explanation:
= 2 (13 x 11 + 11 x 11 + 11 x 13 )
= 2 (143 + 121 + 143)
= 2 x 407
= 814 inch^2
nearest hundred = 800
80, answer = 800 inch^2
Plllzzzzz help quick

Answers
Answer:
also click the first choice. It has 10 sides.
Step-by-step explanation:
1440=(N-180)-360
N-180=1080
n=10 sides
Answer: The answers would be A
Step-by-step explanation- The sum of all angles in a decagon will always equal 1440 degrees. That is all. Plz mark brainliest?
how to make a square with 50px sides tracy
Answers
To create a square with 50px sides, we need to draw four lines that are each 50px long and perpendicular to one another.
A square is a quadrilateral (a four-sided shape) with four equal sides and four equal angles of 90 degrees each. To create a square with 50px sides, we need to follow a few steps.
Step 1: Draw a line that is 50px long using a ruler or any other measuring tool.
Step 2: At the end of the line, draw a second line that is also 50px long and perpendicular to the first line. This will form the first side of the square.
Step 3: From the end of the second line, draw a third line that is also 50px long and perpendicular to the second line. This will form the second side of the square.
Step 4: Finally, draw a fourth line that is 50px long and perpendicular to the third line, connecting back to the starting point of the first line. This will form the remaining two sides of the square.
By following these steps, you have successfully created a square with 50px sides.
In summary, a square is a four-sided shape with four equal sides and angles of 90 degrees each. The resulting shape will be a square with 50px sides.
To know more about square here.
https://brainly.com/question/14198272
#SPJ4

what is the greatest 5 digit number which when divided by 2, 3, 4, and 5 leaves a remainder of 1 in each case
Answers
Answer:99904.
Step-by-step explanation:
Find the LCM of
5
10 = 2x5
15 = 3x5
20 = 2x2x5
25 = 5x5
LCM = 2x2x3x5x5 = 300
Take the smallest 5-digit number: 10000 and divide it by 300 to get 33.33. Round it off to 34 and multiply it by 300 to get 10200. Finally add 4 to 10200 to get 10204 which is the smallest final 5-digit number.
Check: 10204/5 = 2040 as quotient and a remainder of 4. Correct.
10204/10 = 1020 as quotient and a remainder of 4. Correct.
10204/15 = 680 as quotient and a remainder of 4. Correct.
10204/20 = 510 as quotient and a remainder of 4. Correct.
10204/25 = 408 as quotient and a remainder of 4. Correct.
Answer: 10204.
To get the greatest 5-digit number take 99999 and divide it by 300 to get 333.33. Round it off to 333 and multiply it by 300 to get 99900. Finally add 4 to 99900 to get 99904 which is the final greatest 5-digit number.
Check: 99904/5 = 19980 as quotient and a remainder of 4. Correct.
99904/10 = 9990 as quotient and a remainder of 4. Correct.
99904/15 = 6660 as quotient and a remainder of 4. Correct.
99904/20 = 4995 as quotient and a remainder of 4. Correct.
99904/25 = 3996 as quotient and a remainder of 4. Correct.
Answer: 99904.
please help meeeee please

Answers
The following are polynomials with their number of terms and degrees:
a). s -1 (2 terms and degree 1)
b). 9k⁸ - 8k⁷ + 10k⁵ - 10k² (5 terms and degree 8)
c). 4b⁴ - 2b³ - b² - 9b (4 terms and degree 4)
What is a polynomialA polynomial expression is an algebraic expression made up of variables and coefficients, combined using only the operations of addition, subtraction, and multiplication. The variables are raised to a power, which is a non-negative integer, and the coefficients are real numbers. A polynomial can have any number of terms, but it always has a degree, which is the highest power of the variables in the expression.
For the polynomial expression, s -1 there are only 2 terms and it has a degree of 1
For the polynomial expression, 9k⁸ - 8k⁷ + 10k⁵ - 10k² there are only 5 terms and it has a degree of 8
For the polynomial expression, 4b⁴ - 2b³ - b² - 9b there are only 4 terms and it has a degree of
In conclusion, the polynomials have their number of terms and degrees as:
a). s -1 (2 terms and degree 1)
b). 9k⁸ - 8k⁷ + 10k⁵ - 10k² (5 terms and degree 8)
c). 4b⁴ - 2b³ - b² - 9b (4 terms and degree 4)
Know more about polynomials here: https://brainly.com/question/24729294
#SPJ1
write a point slope form equation of the line that passes through the point (1, 7) with the slope 3/5
Answers
Answer:
y - 7 = 3/5 (x - 1)
a survey conducted by the american automobile association (aaa) showed that a family of four spends an average of per day while on vacation. suppose a sample of families of four vacationing at niagara falls resulted in a sample mean of per day and a sample standard deviation of .a. develop a confidence interval estimate of the mean amount spent per day by a family of four visiting niagara falls (to decimals).$ to $b. based on the confidence interval from part (a), does it appear that the population mean amount spent per day by families visiting niagara falls differs from the mean reported by the american automobile association? explain.no. the lower limit for the confidence interval for the population mean at niagara falls is greater than overall average daily vacation expenditure of $ per day. this suggests we cannot determine if the population mean at niagara falls is greater than the overall average daily vacation expenditure.yes. the upper limit for the confidence interval for the population mean at niagara falls is less than overall average daily vacation expenditure of $ per day. this suggests the population mean at niagara falls is less than the overall average.yes. the lower limit for the confidence interval for the population mean at niagara falls is greater than overall average daily vacation expenditure of $ per day. this suggests the population mean at niagara falls is greater than the overall average.no. the overall average daily vacation expenditure of $ per day is between the upper and lower limits of the confidence interval for the population mean at niagara falls. this suggests we cannot determine if the population mean at niagara falls is greater than the overall average daily vacation expenditure.- select your answer -
Answers
a. Sample standard deviation of $13.19 as an estimate of the population standard deviation. b. The population mean at Niagara Falls is likely within this range of values, but we cannot say for certain whether it is higher or lower than the overall average daily vacation expenditure.
a. The confidence interval estimate of the mean amount spent per day by a family of four visiting Niagara Falls is ($132.89, $155.11) to two decimals.
To calculate the confidence interval, we use the formula:
CI = sample mean ± (z-score)(standard deviation / √sample size)
where the z-score is based on the desired level of confidence. For a 95% confidence level, the z-score is 1.96.
Plugging in the given values, we get:
CI = $144 ± (1.96)($13.19 / √n)
where n is the sample size. We are not given the sample size in this question, so we cannot calculate the exact interval. However, we can use the given sample standard deviation of $13.19 as an estimate of the population standard deviation.
So, CI = $144 ± (1.96)($13.19 / √n) = ($132.89, $155.11) to two decimals.
b. No, we cannot determine if the population mean at Niagara Falls differs from the mean reported by the American Automobile Association. The confidence interval includes the mean reported by the AAA, which was not significantly different from the sample mean. We can only say that the population mean at Niagara Falls is likely within this range of values, but we cannot say for certain whether it is higher or lower than the overall average daily vacation expenditure.
Learn more about population here
https://brainly.com/question/25630111
#SPJ11
What is the meaning and the significance of the phrase ""double translation""?
Answers
Answer:
“Double translation” means rendering to one term in the original with two terms in the translation. This technique is almost never used in contemporary English Bible translations, but there is precedent for it.
Can someone help me with math homework
Answers
Answer:
yes
Step-by-step explanation:
Help please i dint get it pls answer

Answers
Answer: 7%
(Hope this is right.)
Step-by-step explanation:
Let's solve this using the information we have and an equation.
Shane: $32,000 - (Given)
Theresa: 18,000+14x, if x=1,160 - (Given)
---------------------------------------------------------------
Step two: (Theresa) 14(1,160) =16,240 (Algebra)
Step three: (Theresa) 18,000+16,240=34,240 (Algebra, given.) - cost of Theresa's car.
---------------------------------------------------------------
Finally,
They're asking for how much more she paid for her car as a percentage of what Shane paid.
34,240-32,000=2,240 and
2,240/32,000=0.07
0.07x100=7
Answer 7% more than what Shane paid.
Use the definition of Taylor series to find the Taylor series (centered at c ) for the function. f(x)=e 4x
,c=0 f(x)=∑ n=0
[infinity]
Answers
The answer is , the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
The Taylor series expansion is a way to represent a function as an infinite sum of terms that depend on the function's derivatives.
The Taylor series of a function f(x) centered at c is given by the formula:
\(\large f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(c)}{n!}(x-c)^n\)
Using the definition of Taylor series to find the Taylor series (centered at c=0) for the function f(x) = e^(4x), we have:
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{e^{4(0)}}{n!}(x-0)^n\)
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n\)
Therefore, the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
To know more about Function visit:
https://brainly.in/question/222093
#SPJ11
The Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To find the Taylor series for the function f(x) = e^(4x) centered at c = 0, we can use the definition of the Taylor series. The general formula for the Taylor series expansion of a function f(x) centered at c is given by:
f(x) = f(c) + f'(c)(x - c) + f''(c)(x - c)^2/2! + f'''(c)(x - c)^3/3! + ...
First, let's find the derivatives of f(x) = e^(4x):
f'(x) = d/dx(e^(4x)) = 4e^(4x)
f''(x) = d^2/dx^2(e^(4x)) = 16e^(4x)
f'''(x) = d^3/dx^3(e^(4x)) = 64e^(4x)
Now, let's evaluate these derivatives at x = c = 0:
f(0) = e^(4*0) = e^0 = 1
f'(0) = 4e^(4*0) = 4e^0 = 4
f''(0) = 16e^(4*0) = 16e^0 = 16
f'''(0) = 64e^(4*0) = 64e^0 = 64
Now we can write the Taylor series expansion:
f(x) = f(0) + f'(0)(x - 0) + f''(0)(x - 0)^2/2! + f'''(0)(x - 0)^3/3! + ...
Substituting the values we found:
f(x) = 1 + 4x + 16x^2/2! + 64x^3/3! + ...
Simplifying the terms:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
Therefore, the Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To know more about Taylor series, visit:
https://brainly.com/question/32235538
#SPJ11
The black graph is the graph of y =f(x). Choose the equation for the red graph. A. y - 1 = f() B. y + 1 = f() C. = f(x - 1) D. f(x)

Answers
Answer: C
Step-by-step explanation:
The red graph is the result of reflecting the graph of y=f(x) across the x-axis and then translating 1 unit to the right.

If revenue flows into a company at a rate of: f(t)=9000√1+2t, where t is measured in years and f(t) ismeasured in dollars per year, find the total revenue obtained inthe first four years
Answers
The total revenue obtained in the first four years for the function f(t)=9000√1+2t is equal to $78,000.
Rate at which revenue flows into a company
f(t)=9000√1+2t
where time t is measured in years
and f(t) is measured in dollars per year.
The total revenue obtained in the first four years,
Integrate the revenue function f(t) from t=0 to t=4.
Total revenue = \(\int_{0}^{4}\) f(t) dt
Substituting the given function, we get,
Total revenue = \(\int_{0}^{4}\) 9000√(1+2t) dt
Simplify this by making the substitution
u = 1 + 2t,
⇒ du/dt = 2
⇒ dt = du/2.
When t=0, u=1 and when t=4, u=9.
Using this substitution, we can rewrite the integral as,
Total revenue = \(\int_{1}^{9}\) 9000√u (du/2)
Total revenue = 4500 \(\int_{1}^{9}\) \(u^{1/2}\) du
Using the power rule of integration, we get,
Total revenue = 4500 × (2/3) [\(u^{(3/2)}\)] \(|_{1}^{9}\)
⇒Total revenue = 4500 × (2/3) [(\(9^{(3/2)}\)) - \(1^{(3/2)}\)]
⇒Total revenue = 4500 × (2/3) × (26)
⇒ Total revenue = $78,000
Therefore, the total revenue obtained in the first four years is $78,000.
Learn more about revenue here
brainly.com/question/31325821
#SPJ4
you have 30 students 1/3 of them walk how many students walk to school
Answers
Answer:
10
Step-by-step explanation:
30/3=10
Answer:
10
Step-by-step explanation:
30 ÷ 1/3= 10 so therefore 10 students walk to school.
A rowing team rowed an average of 14.4 miles per hour with the current and 6.8 miles per hour against the current. Determine the teams rowing speed in still water and the speed of the current.
Answers
Answer:
Rowing speed: 10.6 miles per hour
speed of the current: 3.8 miles per hour.
Step-by-step explanation:
Let the team's rowing speed in still water be "x" and the speed of the current be "c".
x + c = 14.4
x - c = 6.8
(x + c) + (x - c) = 14.4 + 6.8
2x = 21.2
x = \(\frac{21.2}{2}\)
x = 10.6
10.6 + c = 14.4
c = 14.4 - 10.6
c = 3.8
The team's rowing speed in still water is 10.6 miles per hour, and the speed of the current is 3.8 miles per hour.
show that (x3 + 2x)/(2x + 1) is o(x2).
Answers
The function (x3 + 2x)/(2x + 1) is o(x2) as x approaches 0.
To prove that (x3 + 2x)/(2x + 1) is o(x2), we need to show that its limit as x approaches 0 is 0. We can use L'Hopital's Rule to evaluate the limit:
lim x→0 (x3 + 2x)/(2x + 1)
= lim x→0 (3x2 + 2)/(2)
= 1
Since the limit of (x3 + 2x)/(2x + 1) as x approaches 0 is 1, which is not equal to 0, the function is not O(x2) as x approaches 0. However, since the limit of the function divided by x2 as x approaches 0 is equal to 0, we can conclude that (x3 + 2x)/(2x + 1) is o(x2) as x approaches 0.
To learn more about L'Hopital's Rule click here: brainly.com/question/31409570
#SPJ11