>
→
PQ and RS are in the same plane and do not intersect. What geometric term describes PQ and RS?
perpendicular lines
complementary lines
skew lines
parallel lines
Answers
Answer:
Parallel lines
Step-by-step explanation:
Related Questions
In circle N, KL ≅ ML.
Circle N is shown. Line segments N J, N M, N L, and N K are radii. Lines are drawn to connect each point on the circle to create secants J M, M L, L K, and K J. M L and K L are congruent. The measure of arc J K is (5 x + 24) degrees, the measure of arc J M is (13 x + 2) degrees, the measure of arc M L is (8 x minus 3) degrees, and the measure of arc K L is (7 x + 7) degrees.
What is the measure of Arc J M?
Answers
Answer:
74
Step-by-step explanation:
Write the first expression in terms of the second if the terminal point determined by t is in the given quadrant. sec(t), tan(t); Quadrant II sec(t) =
Answers
So, sec(t) = -1/cos(t) lies in Quadrant II.
The sign of a trigonometric function is determined by the signs of the coordinates of the points on the angle's terminal side. Knowing which quadrant the terminal side of an angle is in allows you to determine the signs of all trigonometric functions. The terminal side of an angle can be found in any of the four quadrants or along the axes in either the positive or negative direction (the quadrantal angles). For the signs of the trigonometric functions, each scenario indicates something different.
In Quadrant II, the value of t is between 90 and 180 degrees. In this quadrant, sine is negative, so tangent and secant are also negative.
For the given expressions:
sec(t) = 1/cos(t)
tan(t) = sin(t)/cos(t)
Since sine is negative in Quadrant II, cosine is also negative, so the reciprocal of cosine, which is secant, is negative in this quadrant.
So, sec(t) = -1/cos(t) in Quadrant II.
To learn more about Trigonometry
Visit; brainly.com/question/29140174
#SPJ4
(a) Prove or disprove that if \( f(n)=O(g(n)) \) and \( f(n)=\Omega(g(n)) \) then \( f(n)=\Theta(g(n)) \)
Answers
the statement is disproved. If \(\(f(n)=O(g(n))\) and \(f(n)=\Omega(g(n))\)\),
then it is NOT necessarily true that \(\(f(n)=\Theta(g(n))\\).
Explanation: Let's take an example, Suppose\(\(f(n)=2n\) and \(g(n)=n\\), then:
\(\(f(n)=2n \leq 2n\)\), so
\(\(f(n)=O(g(n))\)(i) \(f(n)=2n \geq n\)\), so
\(\(f(n)=\Omega(g(n))\)(ii)\)
Now, for \(\(f(n)\)\) to be in \(\(\Theta(g(n))\)\),
we need to find constants c1 and c2 such that \(\(0 \leq c_{1}g(n) \leq f(n) \leq c_{2}g(n)\)\) for all values of n greater than some minimum value \(\(n_{0}\)\).
Now, take \(\(c_{1}=1\)\) and \(\(c_{2}=3\)\)(or any other constants), then:
\(c_{1}g(n)=n\)\(c_{2}g(n)=3n\) So,
\(\(c_{1}g(n)=n \leq 2n = f(n) \leq 3n = c_{2}g(n)\)\)
Thus, we can say that if\(\(f(n)=O(g(n))\) and \(f(n)=\Omega(g(n))\)\),
then it is not necessarily true that \(f(n)=\Theta(g(n))\).
Therefore, the statement is disproved.
To know more about values visit:
https://brainly.com/question/30145972
#SPJ11
8. help will upvote
Question 8 5 pts Differentiate implicitly to find the slope of the curve at the given point. Round to the nearest hundredth if necessary. y³ + yx² + x² - 3y² = 0; (-1, 1)
Answers
The slope of the curve at the given point is -1.33.
To find the slope of the curve at the point (-1, 1) using implicit differentiation, we need to differentiate the given equation with respect to x. Let's proceed with the steps:
Step 1: Differentiate both sides of the equation with respect to x.
d/dx(y³ + yx² + x² - 3y²) = d/dx(0)
Step 2: Apply the chain rule to differentiate each term.
d/dx(y³) + d/dx(yx²) + d/dx(x²) - d/dx(3y²) = 0
Step 3: Simplify the derivatives.
3y²(dy/dx) + 2xy + 2x - 6y(dy/dx) = 0
Step 4: Rearrange the equation to solve for dy/dx, which represents the slope.
(3y² - 6y)(dy/dx) = -2xy - 2x
dy/dx = (-2xy - 2x) / (3y² - 6y)
Step 5: Substitute the given point (-1, 1) into the expression for dy/dx to find the slope at that point.
dy/dx = (-2(-1)(1) - 2(-1)) / (3(1)² - 6(1))
= (2 + 2) / (3 - 6)
= 4 / (-3)
≈ -1.33
Therefore, the slope of the curve at the point (-1, 1) is approximately -1.33.
To learn more about slope here:
https://brainly.com/question/4486609
#SPJ4
The city of London, England, has an
elevation of 11 meters.
Which of these describes the elevation
of London?
below sea level
at sea level
above sea level
Answers
Answer:
above sea level
Step-by-step explanation:
(a) Find the median number of hours per week these Year 12 students spend doing homework(b) Given that 10% of these Year 12 students spend more than k hours per week doing homework, find the value of k.
Answers
a) The median number of hours per week these Year 12 students spend doing homework is 4 hours.
b) If 10% of Year 12 students spend more than k hours per week doing homework, then the value of k is 5.75 hours.
What is the median?The median is a central value or a middle value in a distribution. The number of values in a dataset is an important factor that determines the calculation of the median. It is a value that cuts the data set into two equal parts.
The data set consists of 20 Year 12 students. Sort the data in ascending order (or descending order) and find the middle value. Then, use the formula for calculating the median.
a)The number of hours per week the Year 12 students spend doing homework is given as:
3, 3, 3, 3, 3, 3, 3.5, 3.5, 4, 4, 4, 4, 4.5, 5, 5, 5.5, 6, 7, 8, 8.5
Arrange the data in ascending order:
3, 3, 3, 3, 3, 3, 3.5, 3.5, 4, 4, 4, 4, 4.5, 5, 5, 5.5, 6, 7, 8, 8.5
Now count the data, which gives us 20 numbers. The middle value is the 10th and the 11th numbers, which are both 4.
So the median of the number of hours per week Year 12 students spend doing homework is 4 hours.
b) If 10% of Year 12 students spend more than k hours per week doing homework, then the value of k can be found using the following formula:
100% - 10% = 90%
So, 90% of students study for k hours or less.
So, the value of k can be found using the median. The median value is 4 hours, and 90% of students are studying for k hours or less. Therefore, 10% of students study for more than k hours.
k = 10% more than the value of the 90th percentile value, which is given by: k = 5.5 + ((8-5.5)/10)*1 = 5.5 + 0.25 = 5.75 hours.
Therefore, 10% of Year 12 students spend more than 5.75 hours per week doing homework.
To know more about the "median": https://brainly.com/question/26177250
#SPJ11
15th term is 48, 40th term is 223. determine a, d, and the general formula
Answers
Answer:
\(\mathrm{a=-50,\ d=7,\ general\ formula=7(n-1)-50}\)
Step-by-step explanation:
\(\mathrm{Solution,}\\\mathrm{Given,}\\\mathrm{15^{th}\ term(t_{15})=48}\\\mathrm{or,\ a+14d=48.........(1)}\\\mathrm{And\ 40^{th}\ term(t_{40})=223}\\\mathrm{or,\ a+39d=223......(2)}\\\mathrm{n^{th}\ term(t_n)=\ ?}\\\mathrm{Subtracting\ equation(1)\ from\ (2),}\\\mathrm{25d=175}\\\mathrm{or,\ d=7}\\\mathrm{Now,\ a+14d=48\ or,\ a=48-14d=48-14(7)}\\\mathrm{\therefore a=-50}\)
\(\mathrm{t_n=a+(n-1)d}\\\mathrm{or,\ t_n=-50+(n-1)7}\\\mathrm{\therefore general\ formula=7(n-1)-50}\)
I NEED HELP ON THE FIRST QUESTION ASAP!!!!!!!!

Answers
Answer to question 1 is \(\text{y} \le -\frac{2}{5}\text{x}+100\)
=========================================================
Explanation:
The first task is to find the equation of the line through the given points in the table.
Pick any two points you want. I'll pick (0,100) and (50,80)
Determine the slope:
\((x_1,y_1) = (0,100) \text{ and } (x_2,y_2) = (50,80)\\\\m = \text{slope} = \frac{\text{rise}}{\text{run}} = \frac{\text{change in y}}{\text{change in x}}\\\\m = \frac{\text{y}_{2} - \text{y}_{1}}{\text{x}_{2} - \text{x}_{1}}\\\\m = \frac{80 - 100}{50 - 0}\\\\m = \frac{-20}{50}\\\\m = -\frac{2}{5}\\\\\)
The slope is -2/5.
The y intercept is b = 100 because of the point (0,100)
We go from \(\text{y} = m\text{x}+b\) to \(\text{y} = -\frac{2}{5}\text{x}+100\)
Each point from the table is found on this line. For instance, let's check the point (140,44)
\(\text{y} = -\frac{2}{5}\text{x}+100\\\\44 = -\frac{2}{5}*140+100\\\\44 = -56+100\\\\44 = 44\\\\\)
This confirms (140,44)
I'll let you check the other points.
------------------
Any point on the line mentioned represents a scenario where César spends all of the $50.
If he goes above the line, then he'll spend more than $50. If he goes below, he spends less than $50.
This means we want to shade the region below the boundary line \(\text{y} = -\frac{2}{5}\text{x}+100\)
We'll replace the equal sign with a "less than or equal" sign
We arrive at \(\text{y} \le -\frac{2}{5}\text{x}+100\) as the final answer to question 1.
Answer: Answer to question 1 is =========================================================Explanation:The first task is to find the equation of the line through the given points in the table. Pick any two points you want. I'll pick (0,100) and (50,80) Determine the slope:The slope is -2/5.The y intercept is b = 100 because of the point (0,100)We go from to Each point from the table is found on this line. For instance, let's check the point (140,44)This confirms (140,44)I'll let you check the other points.------------------Any point on the line mentioned represents a scenario where César spends all of the $50.If he goes above the line, then he'll spend more than $50. If he goes below, he spends less than $50.This means we want to shade the region below the boundary line We'll replace the equal sign with a "less than or equal" signWe arrive at as the final answer to question 1.
Step-by-step explanation:
what is the value of m?
__°

Answers
Answer:
62 degrees
Step-by-step explanation:
Answer:
52
Step-by-step explanation:
i know how to subtract
Question 5 of 10
Which pair of functions are inverses of each other?
O A. f(x) = 2 + 15 and g(x) = 12x - 15
O B. f(x) = √3x and g(x) = () ³
O c. f(x) = 3 - 10 and g(x) = +10
3
D. f(x) = 11x-4 and g(x) = +4

Answers
The correct answer is D. f(x) = 11x - 4 and g(x) = (x + 4)/11
To determine which pair of functions are inverses of each other, we need to check if the composition of the functions results in the identity function, which is f(g(x)) = x and g(f(x)) = x.
Let's test each option:
Option A:
f(x) = x/2 + 15
g(x) = 12x - 15
f(g(x)) = (12x - 15)/2 + 15 = 6x - 7.5 + 15 = 6x + 7.5 ≠ x
g(f(x)) = 12(x/2 + 15) - 15 = 6x + 180 - 15 = 6x + 165 ≠ x
Option B:
f(x) = ∛3x
g(x) = (x/3)^3 = x^3/27
f(g(x)) = ∛3(x^3/27) = ∛(x^3/9) = x/∛9 ≠ x
g(f(x)) = (∛3x/3)^3 = (x/3)^3 = x^3/27 = x/27 ≠ x
Option C:
f(x) = 3/x - 10
g(x) = (x + 10)/3
f(g(x)) = 3/((x + 10)/3) - 10 = 9/(x + 10) - 10 = 9/(x + 10) - 10(x + 10)/(x + 10) = (9 - 10(x + 10))/(x + 10) ≠ x
g(f(x)) = (3/x - 10 + 10)/3 = 3/x ≠ x
Option D:
f(x) = 11x - 4
g(x) = (x + 4)/11
f(g(x)) = 11((x + 4)/11) - 4 = x + 4 - 4 = x ≠ x
g(f(x)) = ((11x - 4) + 4)/11 = 11x/11 = x
Based on the calculations, only Option D, where f(x) = 11x - 4 and g(x) = (x + 4)/11, satisfies the condition for being inverses of each other. Therefore, the correct answer is:
D. f(x) = 11x - 4 and g(x) = (x + 4)/11
for such more question on inverses
https://brainly.com/question/15066392
#SPJ8
Consider the following time series y(t): 10, 20, 30, 40, 50 for time periods 1 through 5. Using a moving average of order p = 3, a forecast for time period 6 is
Answers
Using a moving average of order p = 3, a forecast for time period 6 is 46.
The moving average is a mathematical method for calculating a series of averages using various subsets of the full dataset. It is also known as a rolling average or a running average. The moving average smoothes the underlying data and lowers the noise level, allowing us to visualize the underlying patterns and patterns more readily. In other words, a moving average is a mathematical calculation that employs the average of a subset of data at various time intervals to determine trends, eliminate noise, and better forecast future outcomes. Answer: 46.
More on moving average: https://brainly.com/question/32464991
#SPJ11
Please help!!!!!!!! I’ll mark brainliest

Answers
The answers to all the equations are:
(A) f(x) = x + 3 when f(4) ⇒ f(x) = 7(B) f(x) = 2x - 9 when f(5) ⇒ f(x) = 1(C) f(x) = -6x + 2 when f(-3) ⇒ f(x) = 20What do we mean by equations?The equals sign is used in mathematical equations to indicate that two expressions are equal.A mathematical statement that uses the word "equal to" between two expressions with the same value is called an equation.Using 3x + 5 as an example equals 15.Equations come in a wide variety of forms, including linear, quadratic, cubic, and others.Point-slope, standard, and slope-intercept equations are the three main types of linear equations.So, f(x):
(A) f(x) = x + 3 when f(4)
f(x) = x + 3f(x) = 4 + 7f(x) = 7(B) f(x) = 2x - 9 when f(5)
f(x) = 2x - 9f(x) = 2(5) - 9f(x) = 10 - 9f(x) = 1(C) f(x) = -6x + 2 when f(-3)
f(x) = -6x + 2f(x) = -6(-3) + 2f(x) = 18 + 2f(x) = 20Therefore, the answers to all the equations are:
(A) f(x) = x + 3 when f(4) ⇒ f(x) = 7(B) f(x) = 2x - 9 when f(5) ⇒ f(x) = 1(C) f(x) = -6x + 2 when f(-3) ⇒ f(x) = 20Know more about equations here:
brainly.com/question/2972832
#SPJ13
you randomly choose one shape from the bag. find the number of ways the event can occur. find the favorable outcomes of the event

Answers
(a) The number of ways that the event can occur is 6.
(b) Probabilities are :
1) 1/2, 2) 1/6 and 3) 1/3.
(a) Given a bag of different shapes.
Total number of shapes = 6
So, if we select one shape from random,
total number of ways that the event can occur = 6
(b) Number of squares in the bag = 3
Probability of choosing a square = 3/6 = 1/2
Number of circles in the bag = 1
Probability of choosing a circle = 1/6
Number of stars in the bag = 2
Probability of choosing a star = 2/6 = 1/3
Hence the required probabilities are found.
Learn more about Probability here :
https://brainly.com/question/14210034
#SPJ1
Describe the shape of the distribution.
A. It is symmetric.
B. It is uniform.
C. It is bimodal.
D. It is skewed.

Answers
Can someone help me ASAP this is almost due
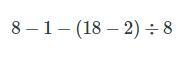
Answers
Answer:
5
Step-by-step explanation:
8-1-(18-2)÷8
PEMDAS says parentheses first
8-1-16÷8
Then divide
8-1-2
Then subtract from left to right
7-2
5
Find the area of the triangle.
The area of the triangle is square units.
Answers
Answer: Um, where is your picture to answer to this question? Please show me this picture to answer the question!
Step-by-step explanation:
Answer:
Step-by-step explanation:
Please your question is Incomplete please edit the question
how many different passwords are possible if each character may be any lowercase letter or digit? please enter your result in scientific notation, making sure the answer in the left box is between 1 and 10.
Answers
From the probability, the quantity of various passwords that are conceivable assuming each character might be any lowercase letter or digit is 2,821,109,907,456 passwords
The most effective method to ascertain the probability
The accompanying information can be concluded:
Number of lower case letters = 26
Number of digits = 10
Total Characters = 26 + 10 = 36
Length of secret word = 8
The quantity of various passwords are conceivable assuming each character might be any lowercase letter or digit will be:
= (26+10)⁸ various passwords
= 2,821,109,907,456 passwords
The quantity of various passwords that are conceivable assuming each character might be any lowercase letter or digit, and something like one person should be a digit will be:
= 36⁸ - 26⁸
= 2,612,282,842,880 passwords
Finally, the probability that a substantial secret phrase will be produced will be:
= (36⁸ - 26⁸)/36⁸
= 0.93
to know more about probability click here:
https://brainly.com/question/25870256
#SPJ4
And angle measure 88. 2 more than a measure of is complimentary angle what is the measure of each angle
Answers
Answer: 90 degrees
Step-by-step explanation: ez
Can you reduce the fraction 28/80
Answers
Answer:
Yes you divide 28/80 by 4 and you get 7/20
Step-by-step explanation:
28/80
is
7/20.
Steps to simplifying fractions
Find the GCD (or HCF) of numerator and denominator
GCD of 28 and 80 is 4
Divide both the numerator and denominator by the GCD
28 ÷ 4
80 ÷ 4
Reduced fraction:
7
20
Therefore, 28/80 simplified to lowest terms is 7/20.
Will make brainliest!!!

Answers
Answer:
For my answer what I got was -118
If its wrong im sorry but I hope this helps :3
HELPPO ASAPPPP PLSS!!

Answers
explication: to find volume you do base * height, 12*3= 36
Answer: A: 288 in cubed B: 180 in cubed
Step-by-step explanation: Volume is length * height * width.
the acme company manufactures widgets. the distribution of widget weights is bell-shaped. the widget weights have a mean of 43 ounces and a standard deviation of 10 ounces.
Answers
The Acme Company manufactures widgets, and the distribution of widget weights is bell-shaped. The mean weight of the widgets is 43 ounces, and the standard deviation is 10 ounces.
A bell-shaped distribution is often referred to as a normal distribution or a Gaussian distribution. In this case, the weights of the widgets follow this distribution pattern. The mean weight of 43 ounces represents the central tendency of the distribution, indicating that the most common or average weight of the widgets is around 43 ounces.
The standard deviation of 10 ounces represents the measure of variability or spread in the widget weights. It quantifies how much the weights of the widgets vary around the mean. A larger standard deviation suggests a wider spread of weights, while a smaller standard deviation indicates a narrower range.
The bell-shaped distribution, with its mean and standard deviation, allows the Acme Company to understand the typical range of widget weights and make informed decisions. It provides valuable insights into the variability and consistency of the manufacturing process, helping ensure that the widgets meet the desired specifications and quality standards.
Learn more about standard deviation here
https://brainly.com/question/29115611
#SPJ11
Share $3423 dollars equally among 7 friends
Answers
Answer:
489
Step-by-step explanation:
3423 divide 7
Which of the data sets below has a total of 7 data points (observations)? A) 18, 91, 93, 55, 57, 18 B) 25, 26, 28, 91, 18 C) 9, 12, 8, 5, 12, 9,7 D) 7,5, 9, 11, 13, 4, 9, 18 E) 95, 91, 87, 99, 95, 84, 77
Answers
To know the number of data points, simply count the number of values in the data, these values are separated by a comma
Option A: 18, 91, 93, 55, 57, 18. is not correct (it has 6 data points)
Option B: 25, 26, 28, 91, 18, is not correct ( it has 5 data points)
Option C: 9, 12, 8,5, 12, 9, 7. is correct (it has 7 data points)
Option D: 7,5, 9, 11, 13, 4, 9, 18. is not correct ( it has 8 data points)
Option E: 95, 91, 87, 99, 95, 84, 77. is correct (it has 7 data points)
Options C and E are correct
HELPP 35 POINTS!! Find the y-intercept of the line on the graph.

Answers
The y-intercept is 2
Answer:
-0.75
Step-by-step explanation:
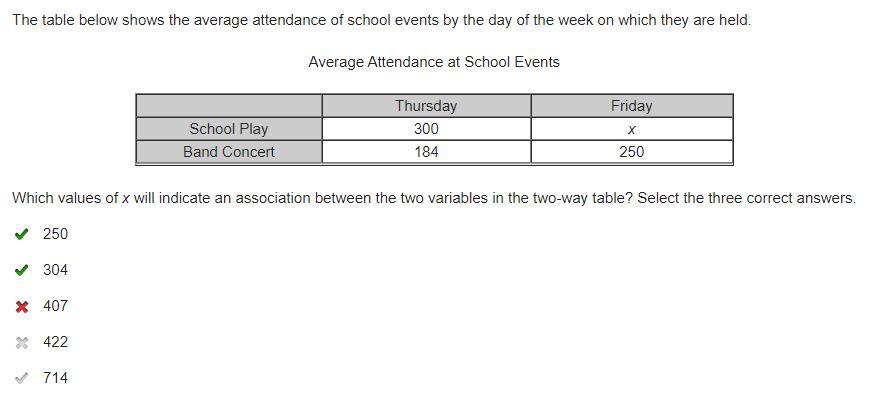
The real answer to the question. The table below shows the average attendance of school events by the day of the week on which they are held. CLick on the file for info. 300 184 250.
Answers
Answer: 407
Step-by-step explanation: Given :
Thursday Friday
School play 300 x
Band concert 184 250
To Find : value of x
Solution
Since we are given that there is an association
So,
Thus the value of x is 407
Answer:
A,B, and E
Step-by-step explanation:
edge 2021
A building was photographed using an aerial camera from a flying height of 1000 m. The photo coordinates of the top of the building on the photo are: 82.501 mm and 62.218 mm, the focal length is 150 m. 1. What is the height of the building? 2. Compute the photographic scale of the building top point.
Answers
If a building was photographed using an aerial camera from a flying height of 1000 m.
1. The height of the building is 5.5 meters.
2. The photographic scale of the building top point is 5.50067e-07.
What is the height?1. Height of the building:
Height of the building = Flying height * (Measured distance / Focal length)
Converting the measured distance from mm to meters:
Measured distance = 82.501 mm * (1 m / 1000 mm)
Measured distance = 0.082501 m
Substituting the values into the formula:
Height of the building = 1000 m * (0.082501 m / 150 m)
Height of the building = 5.5 m
Therefore the height of the building is 5.5 meters.
2. Photographic scale:
Photographic scale = Measured distance / Ground distance
Using the formula for the photographic scale:
Photographic scale = Measured distance / (Flying height * Focal length)
Photographic scale = 82.501 mm / (1000 m * 150 m)
Converting the measured distance from mm to meters:
Measured distance = 82.501 mm * (1 m / 1000 mm)
Measured distance = 0.082501 m
Photographic scale = 0.082501 m / (1000 m * 150 m)
Photographic scale = 5.50067e-07
Therefore the photographic scale of the building top point is 5.50067e-07.
Learn more about height here:https://brainly.com/question/73194
#SPJ4
at a certain grocery checkout counter, the average waiting time is 2.5 minutes. suppose the waiting times follow an exponential density function. (a) write the equation for the exponential distribution of waiting times. e(t) = graph the equation and locate the mean waiting time on the graph. webassign plot webassign plot webassign plot webassign plot (b) what is the likelihood that a customer waits less than 1 minutes to check out? (round your answer to one decimal place.) % (c) what is the probability of waiting between 4 and 6 minutes? (round your answer to one decimal place.) % (d) what is the probability of waiting more than 5 minutes to check out? (round your answer to one decimal place.) % need help? read it
Answers
a) The equation for the exponential distribution of waiting times is given by \(f(x) = \lambda e^{-\lambda x}\)
b) The probability of waiting less than 2 minutes to check out is 0.427
c) The probability of waiting between 4 and 6 minutes is 0.242
d) The probability of waiting more than 5 minutes to check out is 0.082
a. The equation for the exponential distribution of waiting times is given by:
\(f(x) = \lambda e^{-\lambda x}\)
where λ is the rate parameter of the distribution, and e is the natural logarithmic constant (approximately equal to 2.71828). The graph of the exponential distribution is a decreasing curve that starts at λ and approaches zero as x approaches infinity. The mean waiting time, denoted by E(X), is equal to 1/λ.
b. To find the probability that a customer waits less than 2 minutes to check out, we need to calculate the area under the exponential distribution curve between zero and 2 minutes. This can be expressed mathematically as:
P(X < 2) = \(\int_0^2 \lambda e^{-\lambda x} dx\)
Solving this integral yields:
P(X < 2) = 1 - \(e^{(-2\lambda)}\)
Substituting the given average waiting time of 2.5 minutes into the formula for the mean waiting time, we can calculate λ as:
E(X) = 1/λ
2.5 = 1/λ
λ = 0.4
Therefore, the probability of waiting less than 2 minutes to check out is:
P(X < 2) = 1 - \(e^{-2*0.4}\)
P(X < 2) ≈ 0.427
c. To find the probability of waiting between 2 and 4 minutes, we need to calculate the area under the exponential distribution curve between 2 and 4 minutes. This can be expressed mathematically as:
P(2 < X < 4) =\(\int_2^4 \lambda e^{(-\lambda x)} dx\)
Solving this integral yields:
P(2 < X < 4) = \(e^{(-2\lambda)} - e^{(-4\lambda)}\)
Substituting the value of λ obtained in part (b), we get:
P(2 < X < 4) = \(e^{(-20.4)} - e^{(-40.4)}\)
P(2 < X < 4) ≈ 0.242
d. To find the probability of waiting more than 5 minutes to check out, we need to calculate the area under the exponential distribution curve to the right of 5 minutes. This can be expressed mathematically as:
P(X > 5) = \(\int_5^{ \infty} \lambda e^{(-\lambda x)} dx\)
Solving this integral yields:
P(X > 5) = \(e^{(-5\lambda)}\)
Substituting the value of λ obtained in part (b), we get:
P(X > 5) = \(e^{(-5*0.4)}\)
P(X > 5) ≈ 0.082
To know more about probability here
https://brainly.com/question/11234923
#SPJ4
Solve for x :
8x+9-3x=8+5x+1
Answers
Answer:
x=0
Step-by-step explanation:
8x +9-3x=8+5x+1
5x+9=9+5x
5x -5x = 9-9
0=0
solve for A=lw for l. then find the length of a rectangle with a width of 50 millimeters and an are of 250 square millimeters
Answers
Answer:
75
Step-by-step explanation:
\(\frac{250}{2}\)-50
125-50
=75