Given tan 0 9 4) where 0º < 0 < 360°, a) draw a sketch of the angles. Clearly show which quadrants the terminal arm of O lies in and label the principle angle and the related a
Answers
In the given trigonometric expression, tan(θ) = 9/4, where 0° < θ < 360°, we need to sketch the angles and determine in which quadrants the terminal arm of θ lies.
We also need to label the principal angle and the related acute angle.
The tangent function represents the ratio of the opposite side to the adjacent side in a right triangle. The given ratio of 9/4 means that the opposite side is 9 units long, while the adjacent side is 4 units long.
To determine the quadrants, we can consider the signs of the trigonometric ratios. In the first quadrant (0° < θ < 90°), both the sine and tangent functions are positive. Since tan(θ) = 9/4 is positive, θ could be in the first or third quadrant.
To find the principal angle, we can use the inverse tangent function. The principal angle is the angle whose tangent equals 9/4. Taking the inverse tangent of 9/4, we get θ = arctan(9/4) ≈ 67.38°.
Now, let's determine the related acute angle. Since the tangent function is positive, the related acute angle is the angle between the terminal arm and the x-axis in the first quadrant. It is equal to the principal angle, which is approximately 67.38°.
In summary, the sketch of the angles shows that the terminal arm of θ lies in either the first or third quadrant. The principal angle is approximately 67.38°, and the related acute angle is also approximately 67.38°.
To learn more about trigonometric click here:
brainly.com/question/29156330
#SPJ11
Related Questions
At what point should an open circle be drawn?
Answers
The point that should an open circle be drawn exists (0, 0).
What is meant by function ?A formula, rule, or regulation that establishes the link between the independent variable and the dependent variable (the dependent variable). As a set of inputs with one output for each, a function is defined as a relationship between them. A function, expressed simply, is an association between inputs where each input is connected to one and only one output. Generally speaking, there are four different types of functions. based on element One to One Function, Many to One Function, Into Function, One to One and Into Function.The first equation in the system is f(x) = -x, for x < 0.
This means when x=0, f(x) = f(0) = 0.
Since we have the inequality x<0, this means at the point (0, 0),
the point will be open and not filled in.
Therefore, the correct answer is option b) (0, 0).
The complete question is:
The function f(x) is to be graphed on a coordinate plane
At what point should an open circle be drawn?
a) (–1, 0)
b) (0, 0)
c) (0, 1)
d) (1, 0)
To learn more about function refer to:
brainly.com/question/11624077
#SPJ4

An amount of $30,000 is borrowed for 5 years at 4.5% interest, compounded annually. If the loan is paid in full at the end of that period, how m
paid back?
Use the calculator provided and round your answer to the nearest dollar.
Answers
8^-1*5^3/2^-4
Pls answer
Answers
Answer:
I think the awnser is 250
Answer:
8^-1*5^3/2^-4
=250
Step-by-step explanation:
I hope it's help you
Can someone help me ASAP please and thank you

Answers
Answer:48
Step-by-step explanation:
multiply 4 and 12
The probability of a student spending time reading is 0.59, and the probability of a student doing well on an exam and spending time reading is 0.58. What is the probability of a student doing well on an exam given that the student spends time reading
Answers
The probability of a student doing well on an exam given that they spend time reading is approximately 0.983 or 98.3%.
To calculate the probability of a student doing well on an exam given that the student spends time reading, we need to use conditional probability.
Let's denote:
P(R) as the probability of a student spending time reading (P(R) = 0.59),
P(E) as the probability of a student doing well on an exam (P(E)),
P(E|R) as the probability of a student doing well on an exam given that they spend time reading (P(E|R) = 0.58).
The formula for conditional probability is:
P(E|R) = P(E and R) / P(R).
Given that P(E and R) = 0.58 (the probability of a student doing well on an exam and spending time reading) and P(R) = 0.59 (the probability of a student spending time reading), we can substitute these values into the formula:
P(E|R) = 0.58 / 0.59 = 0.983.
Therefore, the probability of a student doing well on an exam given that the student spends time reading is approximately 0.983 or 98.3%.
To know more about probability, visit:
https://brainly.com/question/29120105
#SPJ11
There are 5 white balls,8 red balls ,7 yellow balls and 4 green balls in a container a ball is choosen at random.what is the probabilty of chooseing neither white or green? .
Answers
15/19 + 14/19 = 29/19
Step-by-step explanation:
Add the number of balls in the basket together.
Subtract the number of white balls from the sample space ( the total amount of balls) your answer is written over the sample space and the same process is done for the green ball
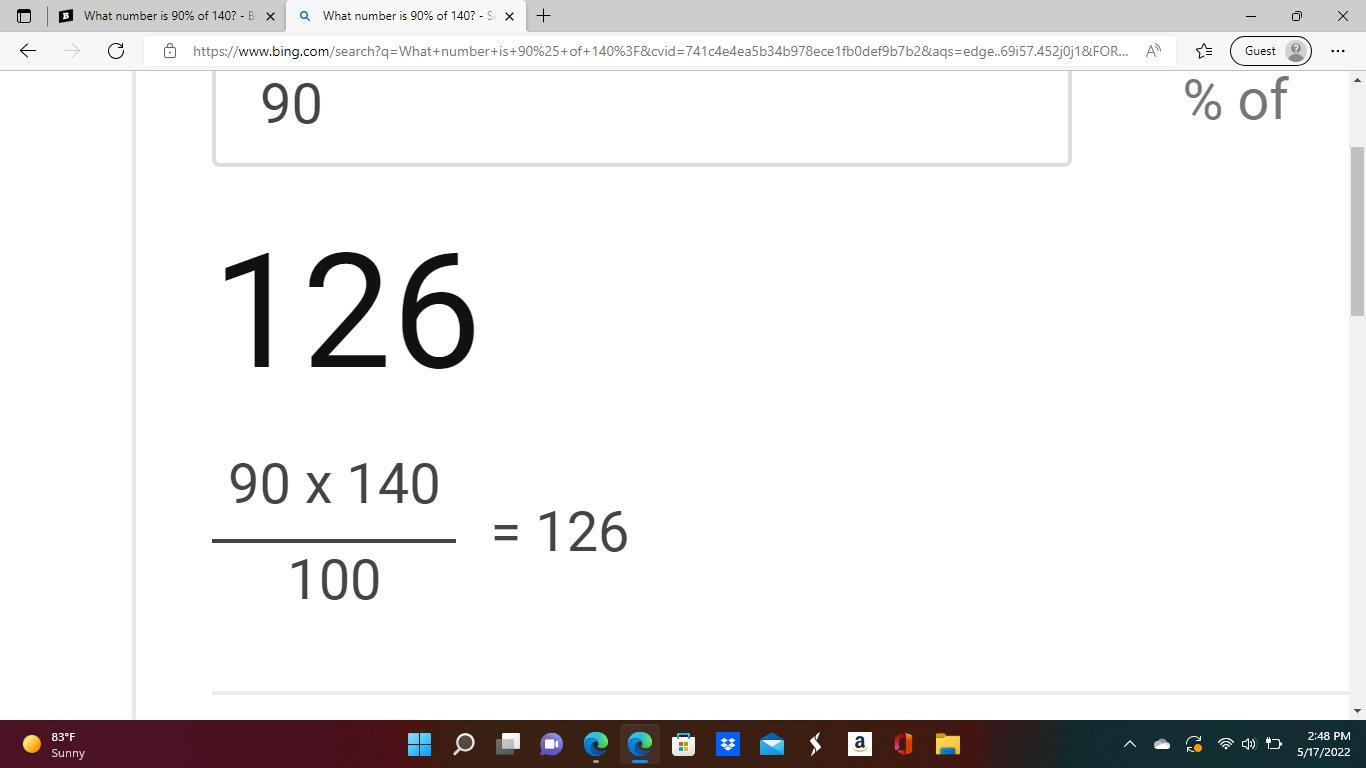
What number is 90% of
140?
Answers
Answer:
126
Step-by-step explanation:
17 years ago i was half the age i am now. how old am i
Answers
17 ÷ 2 = 8.5
A certain positive integer has exactly 20 positive divisors. What is the smallest number of primes that could divide the integer
Answers
As per my explanation to (b) above, the largest number of primes that could factor such a number is 4.
Note that 2,3,5 and 7 are the smallest primes, then use the reasoning from
(b) above. we are looking for four exponents, that, when 1 is added to each and all are multiplied together, would equal 20.
But no such integers k, l, m, and n exist such that (k + 1)(l + 1)(m + 1) (n + 1) = 20 where k, l,m, and n ≥ 1 so this number, whatever it is, can't have 4 prime factors
Let's drop 7 out of the mix and suppose it has just 3 prime factors 2, 3, and 5 again we are looking for three exponents, that, when 1 is added to each and all are multiplied together, would equal 20. Put another way, we are looking for k, l and m ≥ 1 such that (k + 1)(l + 1)(m + 1) = 20
Note that the only possibility here is when we have 2 *2 *5 = 20 and the smallest possible product would be 2^(4 )* 3^(1) * 5^(1) = 2^4 * 3 * 5 = 240
Now......the only remaining possibility is that this number is composed of the two smallest primes, 2 and 3, and we are looking for some k and l ≥ 1 such that (k + 1)(l + 1) = 20 clearly, the only possibilities are when k = 4 and l = 5, or vice-versa
So this number would factor as either 2^3 * 3^4 = 648 or 2^4 * 3^3 = 432 and both are > 240.
Learn more about positive integers at
https://brainly.com/question/1367050
#SPJ4
For what value of a is a(2x+3)=9x+15+x an identity?
Answers
Answer:
Expand the left side, group like terms on both sides, and get
(2a)x + 3a = 10x + 15
To be true for all x, equate like terms from both sides and get
2a = 10
3a = 15
Solution: a = 5
You can test the answer.
Step-by-step explanation:
Expand the left side, group like terms on both sides, and get
(2a)x + 3a = 10x + 15
To be true for all x, equate like terms from both sides and get
2a = 10
3a = 15
Solution: a = 5
You can test the answer.
What is the slope of the function f(x)= 2x - 3?
2
3
-3
-2
Answers
Answer:
slope = 2
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
f(x) = 2x - 3 ← is in slope- intercept form
with slope m = 2
It's no small feat to travel 160,000,000km, to visit 200 million children, in 800 million homes, in only 34 hours... Luckily Santa has magic on his side. If he visits 200,000,000 children in 34 hours, How many Kids per hour.

Answers
Answer
Santa visits 5,882,353 kids per hour
Explanation
The mathematical expression to get the number of kids visited per hour is
\(\text{Number of kids visited per hour = }\frac{Total\text{ number of kids}}{Total\text{ number of hours available}}\)Total number of kids = 200,000,000 kids
Total number of hours available = 34 hours
\(\begin{gathered} \text{Number of kids visited per hour = }\frac{200000000}{34} \\ =5,882,352.94 \\ =5882352\text{ kids per hour to the nearest whole number} \end{gathered}\)Hope this Helps!!!
What is the value of the algebraic expression if x=1/2, y = -1 and z=2?Algebraic Expression: 6x (y to the second power z)A. -12B. -6C. 1D. 6
Answers
The given expression is
\(6xy^2z\)Replacing the given values, we have
\(6\cdot\frac{1}{2}\cdot(-1)^2\cdot(2)=3\cdot1\cdot2=6\)Hence, the answer is D. 6.When constructing a confidence interval, the confidence level is.
Answers
The confidence level in constructing a confidence interval determines the probability that the interval contains the true population parameter. It represents the level of certainty or confidence we have in the accuracy of our estimate.
When constructing a confidence interval, the confidence level is typically chosen in advance and expressed as a percentage, such as 95% or 99%. This level corresponds to the proportion of intervals, calculated from repeated sampling, that would contain the true population parameter. For example, a 95% confidence level means that if we were to construct 100 different intervals using the same method, approximately 95 of them would contain the true parameter. The remaining 5 intervals would not.
A higher confidence level leads to a wider interval, as we need to be more certain about capturing the true parameter. Conversely, a lower confidence level results in a narrower interval, but with a lower level of certainty. It is important to choose an appropriate confidence level based on the desired trade-off between precision and reliability of the estimate.
learn more about parameter here
brainly.com/question/30765873
#SPJ11
Which formula would be used to find the measure of angle 1? one-half(a° b°). one-half(a° "" c°). one-half(b° c°). one-half(a° "" b°).
Answers
The formula one-half(a° - b°) is derived from the fact that the exterior angle of a triangle is equal to one-half the difference between the measures of the two remote interior angles.
To find the measure of angle 1 using the formula one-half(a° - b°), we would simply plug in the known values of a° and b°, and perform the necessary arithmetic operations.
The formula that would be used to find the measure of angle 1 is one-half(a° - b°). This formula applies to a situation where angle 1 is an exterior angle of a triangle, and a° and b° are the measures of the two remote interior angles of the triangle that are adjacent to angle 1. The exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles. Mathematically, this can be expressed as:
angle 1 = a° - b°.
Learn more about angles here :-
https://brainly.com/question/30147425
#SPJ4
16. April Atherton is an accounting clerk with an annual salary of $22,500. Her benefits include $834 for
vacation, $1,300 for health insurance, $1,035 for unemployment insurance, $1,395 for Social Security, and
$326 for Medicare. What is the rate of benefits?
a. 32.9%
c. 42.8%
b. 21.7%
d22.8%
Answers
Answer:B: 42.8%
Step-by-step explanation:because if you subtract all the money she used from the salary she will still have most of her money and I did the math and I got 42.8%
How do i solve this?

Answers
(f - g)(x) = f(x) - g(x)
… = (3x² - 4) - (4x + 1)
… = 3x² - 4x - 5
Right on. Naya's graph has a slope of -3, so the
equation of her line is: y=-3x + 2.
Now type an equation for a different line with a slope
equal to -3.
I
Submit
8
Answers
1/3( 5x - 9) = 2( 1/3x + 6) what is x?
Answers
Answer:
x = 9
Step-by-step explanation:
→Distribute the \(\frac{1}{3}\) to (5x - 9), and the 2 to \((\frac{1}{3} x + 6)\):
\(\frac{1}{3}\)(5x - 9) = 2( \(\frac{1}{3}x\) + 6)
\(\frac{5}{3}x\) + 3 = \(\frac{2}{3}x\)+ 12
→Subtract \(\frac{2}{3}x\) from both sides:
x + 3 = 12
→Subtract 3 from both sides:
x = 9
The value of x from the given equation is 6.
The given equation is 1/3 (5x - 9) = 2(1/3 x + 6).
The solution of an equation is the set of all values that, when substituted for unknowns, make an equation true.
Here, 5x/3 - 9/3 = 2x/3 +6/2
5x/3 -3 = 2x/3 +3
5x/3 -2x/3 =3+3
(5x-2x)/3 = 6
3x/3 = 6
x = 6
Therefore, the value of x from the given equation is 6.
To learn more about an equation visit:
https://brainly.com/question/14686792.
#SPJ6
Use the Central Limit Theorem to find the probability of the indicated event, assuming that the distribution of the population data is unknown. In a certain city, employees work an average of 18.9 hours of overtime every month, with a standard deviation of 7.8 hours. What is the probability that the average number of hours of overtime worked last month by a random sample of 140 employees in the city exceeds 20 hours? Provide a solution showing your calculations and submit your work for marking. Include a sketch as part of your complete solution. P(X > 20)=
Answers
The probability that the average number of hours of overtime worked last month by a random sample of 140 employees in the city exceeds 20 hours is approximately 0.9564, or 95.64%.
To find the probability that the average number of hours of overtime worked by a random sample of 140 employees exceeds 20 hours, we can use the Central Limit Theorem (CLT). The CLT states that for a large enough sample size, the sampling distribution of the sample mean approaches a normal distribution, regardless of the shape of the population distribution.
Given that the population mean is 18.9 hours and the population standard deviation is 7.8 hours, we can calculate the standard error of the mean using the formula: standard error = population standard deviation / sqrt(sample size).
For this problem, the sample size is 140, so the standard error is 7.8 / sqrt(140) ≈ 0.659.
To calculate the probability, we need to standardize the sample mean using the z-score formula: z = (sample mean - population mean) / standard error.
In this case, the sample mean is 20 hours, the population mean is 18.9 hours, and the standard error is 0.659. Plugging these values into the formula, we get z = (20 - 18.9) / 0.659 ≈ 1.71.
Now, we can use a standard normal distribution table or calculator to find the probability associated with a z-score of 1.71. Looking up this value in the table, we find that the probability is approximately 0.9564.
Therefore, the probability that the average number of hours of overtime worked last month by a random sample of 140 employees in the city exceeds 20 hours is approximately 0.9564, or 95.64%.
Here's a sketch to visualize the calculation:
|
|
|
| **
| * *
| * *
| * *
| * *
| * *
| * *
-------------------|--------------------------
18.9 | 20
The area under the curve to the right of 20 represents the probability we're interested in, which is approximately 0.9564 or 95.64%.
for more such questions on probability visit:
https://brainly.com/question/251701
#SPJ8
. During a sale, the price of a computer is reduced by $118 from the original price $590. By what percentage is the price of the computer reduced by? a 25% b. 69% C. 20% d. 75%
Answers
Answer:
C. 20%
Step-by-step explanation:
16 is what percent
of 20?
Answers
Answer:
80%
Step-by-step explanation:
Answer:
The answer is 1=5% so 5 × 16 = 80
HELP PLZ I’m struggling with this

Answers
Answer:
270 per year so 6 years is 1620 and add that with 6000=7620
Find the 50th term of
6, 12, 18, 24,...
Answers
In an Internet trading system, the network is known to go down twice a week on average. What is the maximum number of breakdowns that you can expect in a week with 97.5% confidence
Answers
We can determine that with 97.5% confidence, the maximum number of breakdowns that can be expected in a week would be around four or five.
With 97.5% confidence, the maximum number of breakdowns that can be expected in a week in an Internet trading system is calculated using statistical methods. Given that the network goes down twice a week on average, the upper limit of breakdowns within a week can be determined based on a statistical distribution.
To calculate the maximum number of breakdowns with 97.5% confidence, we can use a statistical approach such as the Poisson distribution. The Poisson distribution is often used to model the number of events that occur within a fixed interval of time, given the average rate of occurrence.
In this case, the average number of breakdowns per week is known to be two. Using the Poisson distribution, we can calculate the upper limit by finding the value of x such that the cumulative probability of x or fewer breakdowns is 97.5%.
By applying statistical calculations or consulting a Poisson distribution table or software, we can determine that with 97.5% confidence, the maximum number of breakdowns that can be expected in a week would be around four or five.
It's important to note that the Poisson distribution assumes certain conditions, such as events occurring independently and at a constant average rate. However, it provides a useful approximation in situations where the number of events follows a similar pattern, as in this case of network breakdowns in an Internet trading system.
Learn more about distribution here
brainly.com/question/33255942
#SPJ11
What is the y-value of the solution to the system of equations? 3x 5y = 1 7x 4y = −13
Answers
The solution to the system of equations is x = -3 and y = 2. The y-value of the solution is 2
To find the y-value of the solution to the system of equations, we can solve the system using any suitable method such as substitution or elimination.
Given system of equations:
3x + 5y = 1
7x + 4y = -13
Let's use the method of elimination to solve the system:
Multiply equation 1 by 4 and equation 2 by 5 to make the coefficients of y in both equations equal:
4(3x + 5y) = 4(1) --> 12x + 20y = 4
5(7x + 4y) = 5(-13) --> 35x + 20y = -65
Now, subtract equation 1 from equation 2 to eliminate the y term:
(35x + 20y) - (12x + 20y) = -65 - 4
35x - 12x = -69
23x = -69
x = -69/23
x = -3
Substitute the value of x into equation 1 to find y:
3(-3) + 5y = 1
-9 + 5y = 1
5y = 1 + 9
5y = 10
y = 10/5
y = 2
Therefore, the solution to the system of equations is x = -3 and y = 2. The y-value of the solution is 2.
For more details of equations :
https://brainly.com/question/21620502
#SPJ4
add the following polynomial of x3+3xy-2×y2+y3,2×3-5x2y-3xy2-2y3
Answers
The addition of the polynomial \(x^{3}+3xy-2xy^{2} +y^{3}\) with \(2x^{3}-5x^{2} y-3xy^{2}-2y^{3}\) is \(3x^{3}+3xy-5x^{2} y-5xy^{2}-y^{3}\).
What is a polynomial?
⇒ A polynomial is an expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables.
⇒ In the addition of polynomials, the like terms are added while in subtraction, the like terms are subtracted.
Calculation;
We have been given two polynomial which we have to add \(x^{3}+3xy-2xy^{2} +y^{3}\) and \(2x^{3}-5x^{2} y-3xy^{2}-2y^{3}\)
The sign after addition or subtraction will always be of the variable having more value.
\((x^{3}+3xy-2xy^{2} +y^{3} )+(2x^{3}-5x^{2} y-3xy^{2}-2y^{3})\)
On adding like terms with each other
⇒ \((x^{3} +2x^{3})+ 3xy-5x^{2} y-(2xy^{2}+3xy^{2})+(y^{3}-2x^{3})\)
⇒ \(3x^{3}+3xy-5x^{2} y-5xy^{2}-y^{3}\)
Hence the addition of the polynomial\(x^{3}+3xy-2xy^{2} +y^{3}\) and \(2x^{3}-5x^{2} y-3xy^{2}-2y^{3}\) is \(3x^{3}+3xy-5x^{2} y-5xy^{2}-y^{3}\).
Learn more about polynomial here :
brainly.com/question/1487158
#SPJ9
Jenny runs a daycare center and charges $60 per day for each child. There are currently 50 children enrolled at the daycare. At a recent conference, Jenny was advised to lower her rates in order to stay competitive in her area. For each price decrease of $4 per day, the number of children enrolled at the center increases by two.
Write the equation that can be used to determine the number of price decreases, x, in dollars, for which the daycare center has a daily revenue of $2,800.
A.
(60 - 4x)(50 + 2x) = 2,800
B.
(60 + 4x)(50 - 2x) = 2,800
C.
(60 - 2x)(50 + 4x) = 2,800
D.
(60 + 2x)(50 - 4x) = 2,800
Answers
Answer:
Step-by-step explanation:
D
a hexagon is graphed ona coordinate grid then translated 7 units to the right and 9 units down. if one of the vertices of the origanal hexgon is located at (-6,6), what is the ordered pair of this vertex of the new hexagon after the translation
Answers
If the graph is translated 7 units to the right and 9 units down , then ordered pair after the translation is (1,-3) .
in the question ,
it is given that
the the hexagon on the coordinate plane is Translated
7 units to the right and
9 units down .
So , on moving the point (-6,6) , 7 units to the right
7 is added to the x coordinate .
hence point is (-6+7,6) = (1,6)
on translating (1,6) , 9 units down
we subtract 6 from the y-coordinate .
the point is (1,6-9) = (1,-3) .
Therefore , If the graph is translated 7 units to the right and 9 units down , then ordered pair after the translation is (1,-3) .
Learn more about Translation here
https://brainly.com/question/10169402
#SPJ1
kiki has a piece of string that she cuts into smaller pieces. this line plot shows the lengths of the pieces. raj has a piece of string that is 12 as long as kiki's third-longest piece. (note: the problem says third-longest piece, not third-longest length.) how long is raj's piece of string? enter your answer as a mixed number in simplest form by filling in the boxes.
Answers
The length of Raj's piece of string is 12x units.
What is the area of a triangle with base length 8 units and height 5 units?To determine the length of Raj's piece of string, we need to find Kiki's third-longest piece.
Looking at the line plot or list of lengths provided, we can identify the third-longest length of Kiki's pieces.
Let's assume Kiki's third-longest piece has a length of x units.
According to the problem, Raj's piece of string is 12 times as long as Kiki's third-longest piece.
Therefore, the length of Raj's piece of string would be 12 × x units.
We can only express it as 12x units, where x represents the length of Kiki's third-longest piece.
Learn more about triangle
brainly.com/question/2773823
#SPJ11