Answers
Already answered here: https://brainly.com/question/26860297
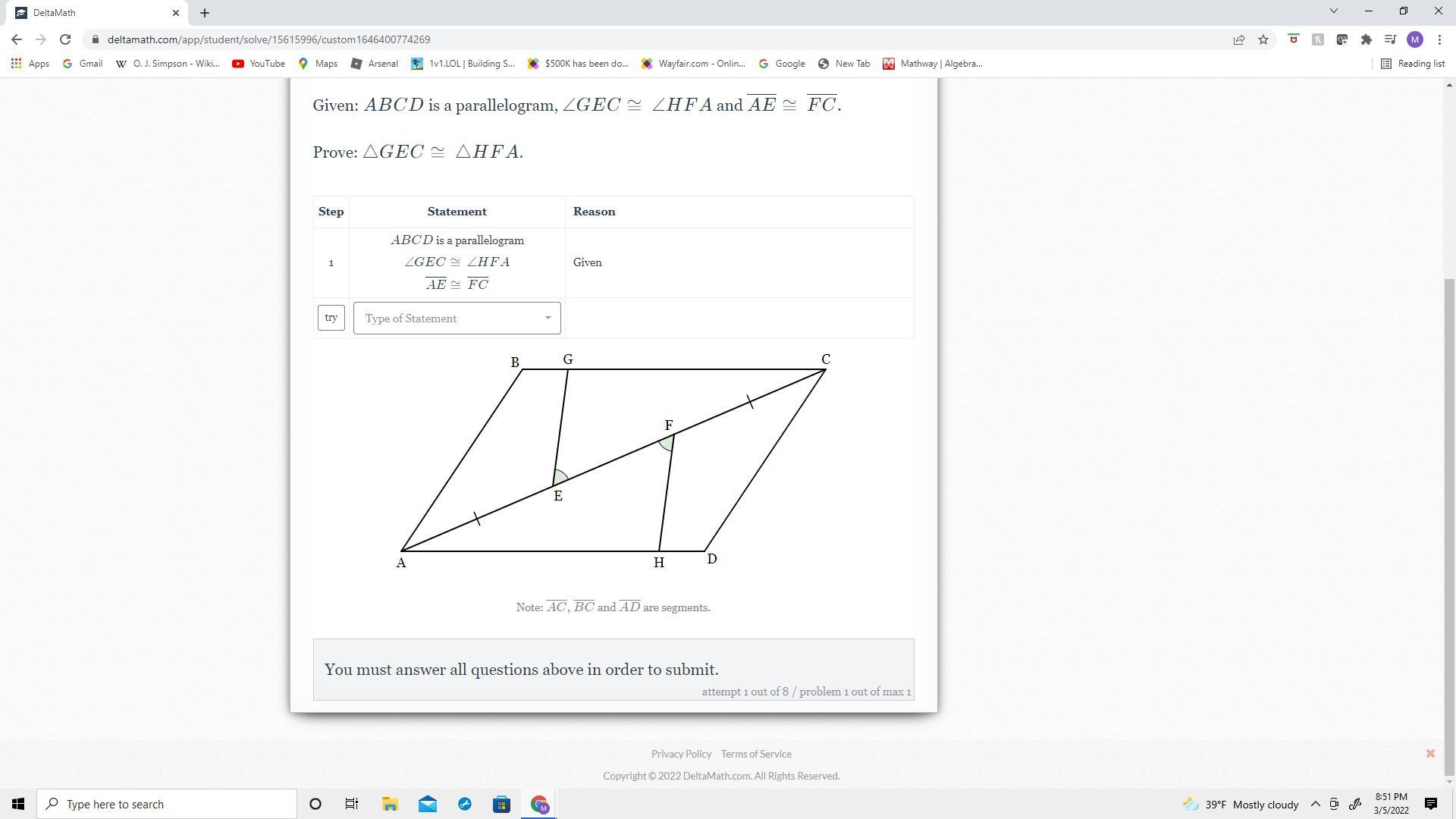
<GEC=<HFA
As
A E=F CA F=E CAlso
GE=FHHenceforth
△GEC ≅ △HFA(SAS congruency)
Related Questions
i really need help i have till 11:00

Answers
The expression that represents the combined inventory of these two stores is given as follows:
A. 7g²/2 - 4g/5 + 15/4.
How to obtain the combined inventory?The combined inventory is obtained adding the inventories for each store, combining the like terms.
The addition of the like terms for g² is given as follows:
1/2 + 3 = 0.5 + 3 = 3.5 = 7/2g².
The term with g is given as follows:
-4g/5.
The constant like terms are combined as follows:
7/2 + 1/4 = 14/4 + 1/4 = 15/4.
Hence the simplified expression is given as follows:
7g²/2 - 4g/5 + 15/4.
Meaning that the correct option is given by option A.
More can be learned about simplification of expressions at https://brainly.com/question/723406
#SPJ1
How many millimeters are in 90 ounces?
Answers
Answer:2661615
Step-by-step explanation:
29573.5 is how many millimeters are in an ounce multiply that by 90 and you get 2661615
hope this helps
Answer:
you used two different types of things ounces measure mass and millimeters measure length
but I used google and it said 2.662e+6
Every ten minutes, Frankie follows a pattern in creating a new group of drawings. Below, you can see how many total drawings Frankie has created by the end of each ten-minute interval.
If he continues to follow this pattern, at the end of seventy minutes, how many total drawings will Frankie have created?
will give 199 points

Answers
Answer: 54 patterns
Step-by-step explanation:
12+17=19+14=33+21=54
Factor: 5x2 – 15x – 20.
(a) 5(x-4)(x+1),
(b) -2(x-4)(x+5),
(c) -5(x+4)(x-1),
(d) 5(x+4)(x+1).
Answers
Answer:
A
Step-by-step explanation:
2) The mean mathematics SAT score in 2012 was 514 with a standard deviation of 117 ("Total group profile," 2012). Assume the mathematics SAT score is normally distributed. a. State the random variable. b. Find the probability that a person has a mathematics SAT score over 700. c. Find the probability that a person has a mathematics SAT score of less than 400. d. Find the probability that a person has a mathematics SAT score between a 500 and a 650. e. Find the mathematics SAT score that represents the top 1% of all scores.
Answers
The mathematics SAT score representing the top 1% of all scores is approximately 780.
a. The random variable in this case is the mathematics SAT score.
b. To find the probability that a person has a mathematics SAT score over 700, we need to calculate the z-score first.
The z-score is calculated as \(\frac{(X - \mu )}{\sigma}\),
where X is the value we're interested in, μ is the mean, and σ is the standard deviation.
In this case, X = 700, μ = 514, σ = 117.
Using the formula, the z-score is \(\frac{(700 - 514)}{117 } = 1.59\).
To find the probability associated with this z-score, we can consult a standard normal distribution table or use a calculator.
The probability is approximately 0.0564 or 5.64%.
c. To find the probability that a person has a mathematics SAT score of less than 400, we again calculate the z-score using the same formula.
X = 400, μ = 514, and σ = 117.
The z-score is \(\frac{(400 - 514) }{117 } = -0.9744\).
Looking up the probability associated with this z-score, we find approximately 0.1635 or 16.35%.
d. To find the probability that a person has a mathematics SAT score between 500 and 650, we need to calculate the z-scores for both values.
Using the formula, the z-score for 500 is \(\frac{(500 - 514)}{117 } = -0.1197\),
and the z-score for 650 is \(\frac{(650 - 514)}{117 } = 1.1624\).
We can then find the area under the normal curve between these two z-scores using a standard normal distribution table or calculator.
Let's assume the probability is approximately 0.3967 or 39.67%.
e. To find the mathematics SAT score that represents the top 1% of all scores, we need to find the z-score corresponding to the top 1% of the standard normal distribution.
This z-score is approximately 2.33.
We can then use the z-score formula to calculate the corresponding SAT score.
Rearranging the formula,
\(X = (z \times \sigma ) + \mu\),
where X is the SAT score, z is the z-score, μ is the mean, and σ is the standard deviation.
Substituting the values,
\(X = (2.33 \times 117) + 514 = 779.61\).
Rounded to the nearest whole number, the mathematics SAT score representing the top 1% of all scores is approximately 780.
For such more questions on mathematics
https://brainly.com/question/29892643
#SPJ8
A
-2+
Which graph represents the
function y = tan x?
B
2T
2T
D
-2+1
21
4+
ㅠ
2T
2πT

Answers
The graph that represents the function y= tanx is Option A.
What is the description of the above function?The graph of y =tan (x) is a periodic function that has vertical asymptotes at x = (n + 1/2)π, where n is an integer.
It oscillates between positive and negative infinity, creating a wave- like pattern.
It has a repeating pattern of sharp peaks and valleys, exhibiting both positive and negative slopes.
Thus, option A is the correct answer.
Learn more about graph:
https://brainly.com/question/25184007
#SPJ1

According to Beautiful Bride magazine, the average age of a groom is now 26.2 years. A sample of 16 prospective grooms in Chicago revealed that their average age was 26.6 years with a standard deviation of 5.3 years. At a=0.05, what is the test value?
Answers
Answer:
0.3019
Step-by-step explanation:
Null hypothesis: the average age of a groom is now 26.2 years.
Alternative hypothesis: the average age of a groom is not 26.2 years.
We have a sample of 16 so we will use a t-test
Where t score = (x-u)/(sd/√n)
Where x = 26.6, u=26.2, sd= 5.3 and n=16
t score = (26.6-26.2) / (5.3/√16)
t = 0.4/(5.3/4)
t = 0.4/1.325
t = 0.3019
Which sentence uses correct grammar to describe the situation?
Three boys brought comic books to class. Their teacher has taken all of the books and placed them on her desk.
The boy's comic books are on the teacher's desk.
The boy's comic books are on the teachers' desk.
The boys' comic books are on the teacher's desk.
The boys' comic books are on the teachers' desk.
Question 8(Multiple Choice Worth 5 points)
(MC)
You want to turn each of the following words into an adverb. Which word would require you to add ally instead of ly?
Certain
Comic
Original
Quick
Answers
Answer:
The boys' comic books are on the teacher's desk
comically
Step-by-step explanation:
Use the formula y = Kx to find K when:
a. x = 3, y = 21 , K =
b. x = 4, y = 24, K =
Answers
Step-by-step explanation:
a.
\(y = kx \\ 21 = k \times 3 \\ 21 \div 3 = \frac{(k \times 3)}{3} \\ 7 = k\)
b.
\(y = kx \\ 24 = k \times 4 \\ \frac{24}{4} = \frac{(k \times 4)}{4} \\ 6 = k\)
From the top of a lighthouse 82 m tall, a guard sees two ships at sea.
The angle of depression to the closer ship is 53° and to the further ship is 39°.
How far are the ships apart from each other to the nearest metre?

Answers
The distance between the two ship based on the angle of depression is 42 meters.
The distance of each ship can be calculated thus:
TanX = opposite / Adjacent
The first ship:
Tan53 = distance/ 82
distance= 108.82 meters
The second ship:
Tan39 = distance/ 82
distance= 66.40 meters
The Difference between the ships are :
108.82 - 66.40 = 42.42 metersTherefore, the distance between the two ships is 42 meters.
Learn more on angles of depression:https://brainly.com/question/17193804
#SPJ1
Multiply..........
\( \large \rm \: i)1 \frac{5}{11} \times 12 \: \: \: \: \: \: \: ii)1 \frac{7}{12} \times 21\)
Answers
\(i) \: \:1 \times \frac{5}{11} \times 12\)
\( = \frac{16}{11} \times 12\)
\( = \frac{192}{11} \)
\(ii) \: \: 1 \times \frac{7}{12} \times 21\)
\( = \frac{19}{12} \times 21\)
\( = \frac{19}{4} \times 7\)
\( = \frac{133}{4} answer\)
The required product of the expression are 17 5/11 and 33 1/4 respectively
Multiplication of mixed fractionsGiven the following products
1) 1 5/11 * 12
This can also be expressed as:
1) 16/11 * 12
= 192/11
= 17 5/11
For the product 1 7/12 * 21
2) 19/12 * 21
= 399/12
= 33 1/4
Hence the required product of the expression are 17 5/11 and 33 1/4 respectively
Learn more on the product here: https://brainly.com/question/1755985
laura opened a savings account with an initial of $200. Each month she adds $50 to the account. Write an equation that would model this situation.
Answers
Answer:
200+50x
Step-by-step explanation:
your friend earns $10 babysitting. This is 3 more than you earn for washing the car. How much do you make for washing the car
Answers
Answer:
$7
Step-by-step explanation:
$10 - $3 = $7
On the coordinate plane below, what is the length of AB?

Answers
Answer:
Ok so i think you can just count it i dont know; edit : i counted, it turns out the answer is 15 :)
A paint mixer wants to mix paint that is 30% gloss with paint that is 15% gloss to make 3.75 gallons of paint that is 20% gloss. How many gallons of each paint should the paint mixer mix together?
Answers
Answer:
1.25 gallons of 30% gloss and 2.5 gallons of 15% glossStep-by-step explanation:
Gloss content is same at the input and output.
Let 30% gloss is x gallons, then 15% gloss is (3.75 - x) gallons.
We have the following equation:
0.3x + 0.15(3.75 - x) = 0.2*3.750.3x + 0.5625 - 0.15x = 0.750.15x = 0.75 - 0.56250.15x = 0.1875x = 0.1875/0.15x = 1.25 gallonsAmount of 15% gloss:
3.75 - 1.25 = 2.5 gallons30% gloss is 1.25 gallons and 15% gloss is 2.5 gallons
NO LINKS!! URGENT HELP PLEASE!!!!!
Express in terms of logarithms of x, y, z, or w.
a. log_7(xz)
b. log_7(y/x)
c. log_7(cube root of z)
Answers
Answer:
a.\(\bold{log_7(xz) = log_7(x * z) = log_7(x) + log_7(z)}\)
b.\(\bold{log_7(\frac{x}{y}) = log_7(y) - log_7(x)}\)
c.\(\bold{log_7(\sqrt[3]{7} ) = log_7(z^{\frac{1}{3}}) = \frac{1}{3}log_7(z)}\)
Step-by-step explanation:
let me provide an explanation for each of the expressions.
a. To express log_7(xz) in terms of logarithms of x and z, we use the logarithmic property that states log(a * b) = log(a) + log(b). Applying this property, we get:\(\bold{log_7(xz) = log_7(x * z) = log_7(x) + log_7(z)}\)
b. To express log_7(y/x) in terms of logarithms of y and x, we use the logarithmic property that states log(a / b) = log(a) - log(b). Applying this property, we get:\(\bold{log_7(\frac{x}{y}) = log_7(y) - log_7(x)}\)
c. To express log_7(cube root of z) in terms of the logarithm of z, we use the logarithmic property that states log(a^(n)) = n * log(a), where n is a constant. Applying this property, we get:\(\bold{log_7(\sqrt[3]{7} ) = log_7(z^{\frac{1}{3}}) = \frac{1}{3}log_7(z)}\)
Therefore, we can express each of the given expressions in terms of logarithms of x, y, z, or w using the logarithmic properties mentioned above.
Answer:
\(\textsf{a.} \quad \log_7(x) + \log_7(z)\)
\(\textsf{b.} \quad \log_7(y) - \log_7(x)\)
\(\textsf{c.} \quad \dfrac{1}{3}\log_7(z)\)
Step-by-step explanation:
We can express the given logarithmic expressions in terms of x, y, z or w by using the laws of logarithms.
\(\hrulefill\)
Part (a)\(\boxed{\begin{array}{c}\underline{\textsf{Product law}}\\\\ \log_a(bc)=\log_a(b) + \log_a(c)\\\end{array}}\)
By using the log product law, we can express log₇(xz) as:
\(\log_7(xz) =\log_7(x) + \log_7(z)\)
\(\hrulefill\)
Part (b)\(\boxed{\begin{array}{c}\underline{\textsf{Quotient law}}\\\\\log_a \left(\dfrac{b}{c}\right)=\log_a(b) - \log_a(c)\end{array}}\)
By using the log quotient law, we can express log₇(y/x) as:
\(\log_7 \left(\dfrac{y}{x}\right)=\log_7(y) - \log_7(x)\)
\(\hrulefill\)
Part (c)\(\boxed{\begin{array}{c}\underline{\textsf{Power law}}\\\\\log_ax^n=n\log_ax\end{array}}\)
By using the log power law, we can express log₇(∛z) as:
\(\begin{aligned}\log_7 \left(\sqrt[3]{z}\right)&=\log_7 \left(z^{\frac{1}{3}\right) \\&=\dfrac{1}{3}\log_7(z)\end{aligned}\)
Which of the following numbers sets does not include \large -\sqrt{25} ?
a
Integers
b
Whole Numbers
c
Real Numbers
d
Rational Numbers
Answers
Answer:
Step-by-step explanation:
The answer is B
The whole numbers are the + integer set. Since -sqrt(25) = - 5, this number is not included in the whole number set.
what is the difference of twice a number and 3 is 11
Answers
Answer:
2x - 3 = 11
x = -21
Step-by-step explanation:
What is the equation of the line that passes through the point (-4,1) and has a slope of -5/4
Answers
Answer:
y = -5/4x -4
Step-by-step explanation:
slope(m)= -5/4
x1=-4,y1=1
using the formula for one point form
y-y1=m(x-x1)
y-1= -5/4(x-(-4))
y-1 = -5/4x + -5/4 × +4
y - 1 = -5/4x -5
y=-5/4x -5 + 1
y = -5/4x -4.
Don't forget to smash the answer as brainliest if I truly deserve it
Thanks
Find the equation of the given line.

Answers
Answer:
y=2/3x+1
Step-by-step explanation:
m= (slope)
b= (y-intercept
Why is 4 + (-3) equal to 1?
Answers
Step-by-step explanation:
4+(-3)=1
because when you open brackets + and - will be -, so 4-3=1
in 2011 there were 3223 sea otters in Monterey Bay California the bay is approximately 77 mi.² to the nearest whole number what was the density of the sea otter population
Answers
Answer:
42 sea otters per mi2
Step-by-step explanation:
17 The table below shows the distance a car has traveled.
50
20
f
40
Minutes
Distance
Traveled
(in miles)
What is the meaning of the slope of the linear model for the data?
60
100
a) The car travels 5 miles every minute.
b) The car travels 4 miles every minute.
c) The car travels 4 miles every 5 minutes.
d) The car travels 5 miles every 4 minutes.
125
80
100
Answers
Given statement solution is :- None of the given options (a, b, c, or d) match the meaning of the slope. The correct interpretation is that the car travels approximately 0.8 miles every minute.
To determine the meaning of the slope of the linear model for the given data, let's analyze the information provided. The table represents the distance traveled by a car at different time intervals.
Minutes | Distance Traveled (in miles)
50 | 20
20 | f
40 | 60
100 | a
125 | 80
100 | 100
To find the slope of the linear model, we need to calculate the change in distance divided by the change in time. Let's consider the intervals where the time changes by a fixed amount:
Between 50 minutes and 20 minutes: The distance changes from 20 miles to 'f' miles. We don't have the exact value of 'f', so we can't calculate the slope for this interval.
Between 20 minutes and 40 minutes: The distance changes from 'f' miles to 60 miles. Again, without knowing the value of 'f', we can't calculate the slope for this interval.
Between 40 minutes and 100 minutes: The distance changes from 60 miles to 'a' miles. We don't have the exact value of 'a', so we can't calculate the slope for this interval.
Between 100 minutes and 125 minutes: The distance changes from 'a' miles to 80 miles. Since we still don't have the exact value of 'a', we can't calculate the slope for this interval.
Between 125 minutes and 100 minutes: The distance changes from 80 miles to 100 miles. The time interval is 25 minutes, and the distance change is 100 - 80 = 20 miles.
Therefore, based on the given data, we can conclude that the car travels 20 miles in 25 minutes. To determine the meaning of the slope, we divide the distance change by the time change:
Slope = Distance Change / Time Change
= 20 miles / 25 minutes
= 0.8 miles per minute
So, none of the given options (a, b, c, or d) match the meaning of the slope. The correct interpretation is that the car travels approximately 0.8 miles every minute.
For such more questions on Car travels
https://brainly.com/question/32301907
#SPJ8
Pablo used a total of 5 3/4 gallons of gas while driving his car. Each hour he was driving, he used 5/6 gallons of gas. What was the total number of hours he was driving? Write your ans
Answers
We know that he used 5/6 gallons of gas per hour of driving.
So, the total amount of gas he used is 5/6 * x.
We also know that he used a total of 5 3/4 gallons of gas.
So, we can set up the equation:
5/6 * x = 5 3/4
To solve for x, we can first convert 5 3/4 to an improper fraction:
5 3/4 = 23/4
Then, we can multiply both sides of the equation by the reciprocal of 5/6:
x = (5 3/4) / (5/6)
x = (23/4) / (5/6)
x = (23/4) * (6/5)
x = 27.6/4
x = 6.9
Therefore, Pablo was driving for a total of 6.9 hours.
brainliest???
Which of the following probabilities is the greatest for a standard normal distribution?
O P(-1.55zs-0.5)
O P(-0.5 Sz50.5)
P(0.5 <251.5)
O P(1.5 sz<2.5)
Answers
Answer:
B
Step-by-step explanation:
On edge
The probabilities is the greatest for a standard normal distribution is
P(-0.5 ≤ z ≤ 0.5) = 0.382.
What is Normal Distribution?An example of a continuous probability distribution is the normal distribution, in which the majority of data points cluster in the middle of the range while the remaining ones taper off symmetrically towards either extreme. The distribution's mean is another name for the centre of the range.
From the diagram attached below, we can write
1. P( -1.55 ≤ z ≤ -0.5)
= 0.092 + 0.15
= 0.242
or, 9.2%+15%=24.2%.
2. P( -0.5 ≤ z ≤ 0.5)
= 0.191 + 0.191
= 0.382
3. P( 0.5 ≤ z ≤ 1.5)
= 0.15 + 0.092
= 0.242
4. P( 1.5 ≤ z ≤ 2.5)
= 0.044 + 0.017
= 0.061
So, the greatest value is P(-0.5 ≤ z ≤ 0.5) = 0.382
Learn more about Normal Distribution here:
https://brainly.com/question/1470443
#SPJ7
[IMAGE ATTACHED]
Please help me with 9
![[IMAGE ATTACHED]Please help me with 9](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/tMkZZac4RitMCkl4x1W4xtaN2wI6rn1W.png)
Answers
Answer:
C=35x+75
It would cost $425 for 15 people
Step-by-step explanation:
DO
Below is the graph of a system of two linear equations.
Ay-aus
-9-8-7-5-5
578
x-axs
What system does it represent, and what is the solution of this system?
O y = x - 6 and x + y =
-2; solution = (2, -4)
O
O y = x - 6 and y - x =
y = x - 6 and y - x =
O y = x-6 and x + y =
-2; solution = (2, - 4)
-2; solution = (-4,2)
-2; solution = (-4, 2)

Answers
The system of equations represented by the graph is:
y = x - 6
y + x = -2
And the solution is (2, -4), then the correct option is the first one.
What system is represented by the graph?
On the graph, we can see a system of linear equations, we can see a line with a positive slope and a line with a negative slope.
The line with a positive slope intercepts the y-axis at y = -6, then that line is:
y = a*x - 6
with a > 0.
The other line passes through the y-axis at y = -2, then the linear equation is:
y = b*x - 2
Where b < 0.
Also, remember that the solution for the system of equations is the point where the two lines intersect, so we can see that the solution is at (2, -4)
The only option that meets all the criteria is the first option:
y = x - 6
x + y = -2
And the solution is (2, -4)
Learn more about systems of equations:
https://brainly.com/question/13729904
#SPJ1
Order the expressions from least to greatest.
3^2
2^3– 2^1
2^1+3^1

Answers
Answer:
2¹+3¹ , 2³ -2¹ , 3²
Step-by-step explanation:
to know the magnitude of the value of each expression 3² =9 ,
2³ -2¹ =8-2=6
2¹ +3¹ = 5
Find the height of the tower using the information given in the illustration.

Answers
using SOH CAH TOA
Tan 85.144 =h/130
h=tan 85.144*130
h=1530.19 fr

consider the initial value problem find the value of the constant and the exponent so that is the solution of this initial value problem.
Answers
The value of the constant, c is 4 and the value of the exponent, r is 2.
To find the solution to this initial value problem, we need to solve for c and r.
First, we can divide both sides of the equation by 2t:
y′ = 2y/t
Next, we can separate the variables:
dy/y = 2dt/t
Integrating both sides, we get:
ln|y| = 2ln|t| + C
Exponentiating both sides:
|y| = Ce^(2ln|t|) = \(C(|t|^2)\)
Since y can be negative or positive, we can write:
y = ±C\(|t|^2\)
To find the value of C, we can use the initial condition y(2) = −8:
−8 = ±C(\(2^2\))
Solving for C, we get:
C = −4
The following is the answer to the starting value problem:
y = −\(4|t|^2\)
Note that \(|t|^2\) = \(t^2\) for positive t and \(|t|^2\) = -\(t^2\) for negative t, so we can write:
y = -4\(t^2\) for t > 0
y = 4\(t^2\) for t < 0
So the value of c is 4 and the value of r is 2.
The complete question is:-
Consider the initial value problem 2ty′=4y, y(2)=−8. 2ty′=4y, y(2)=−8. find the value of the constant c and the exponent r so that y=ctry=ctr is the solution to this initial value problem.
To learn more about exponent, refer:-
https://brainly.com/question/30066987
#SPJ4