Answers
The value of y is 7
Here, we are interested in finding the value of y
From the angle markings of the triangle, we can see that what we have is an isosceles triangle
In an isosceles triangle, the base angles are equal which in this case also makes the sides facing the angles equal
Thus, mathematically;
\(\begin{gathered} 8(y+2)\text{ = 72} \\ \\ y\text{ + 2 = }\frac{72}{8} \\ \\ y\text{ + 2 = 9} \\ \\ y\text{ = 9-2} \\ \\ y\text{ = 7} \end{gathered}\)Related Questions
Pleaseee helpppp meeeeee!

Answers
Right triangle EFG has its right angle at F, EG = 6 , and FG = 4 What is the value of the trigonometric ratio of an angle of the triangle? Drag a value to each box to match the trigonometric ratio with its value .

Answers
Answer:
\(\cos G=\dfrac{2}{3}\)
\(\csc E=\dfrac{3}{2}\)
\(\cot G=\dfrac{2}{\sqrt{5}}\)
Step-by-step explanation:
If the right angle of right triangle EFG is ∠F, then EG is the hypotenuse, and EF and FG are the legs of the triangle. (Refer to attached diagram).
Given ΔEFG is a right triangle, and EG = 6 and FG = 4, we can use Pythagoras Theorem to calculate the length of EF.
\(\begin{aligned}EF^2+FG^2&=EG^2\\EF^2+4^2&=6^2\\EF^2+16&=36\\EF^2&=20\\\sqrt{EF^2}&=\sqrt{20}\\EF&=2\sqrt{5}\end{aligned}\)
Therefore:
EF = 2√5FG = 4EG = 6\(\hrulefill\)
To find cos G, use the cosine trigonometric ratio:
\(\boxed{\begin{minipage}{9 cm}\underline{Cosine trigonometric ratio} \\\\$\sf \cos(\theta)=\dfrac{A}{H}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
For angle G, the adjacent side is FG and the hypotenuse is EG.
Therefore:
\(\cos G=\dfrac{FG}{EG}=\dfrac{4}{6}=\dfrac{2}{3}\)
\(\hrulefill\)
To find csc E, use the cosecant trigonometric ratio:
\(\boxed{\begin{minipage}{9 cm}\underline{Cosecant trigonometric ratio} \\\\$\sf \csc(\theta)=\dfrac{H}{O}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
For angle E, the hypotenuse is EG and the opposite side is FG.
Therefore:
\(\csc E=\dfrac{EG}{FG}=\dfrac{6}{4}=\dfrac{3}{2}\)
\(\hrulefill\)
To find cot G, use the cotangent trigonometric ratio:
\(\boxed{\begin{minipage}{9 cm}\underline{Cotangent trigonometric ratio} \\\\$\sf \cot(\theta)=\dfrac{A}{O}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
For angle G, the adjacent side is FG and the opposite side is EF.
Therefore:
\(\cot G=\dfrac{FG}{EF}=\dfrac{4}{2\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)

ava rents the snowboard for 4 days . Lucia rents the boots for 5 days . What is the total cost of the rentals ?
Answers
whatever how much the money is for one day on the object just multiply the money by the days it's rented out and add together the snowboard total and the boots total
Answer:
358
Step-by-step explanation:
find the product of -5x to the 2nd power y to the 4th power and 3xy to the 3rd power
Answers
Explanation:
-5x to the 2nd powe is: (-5x)² = (-5)²x² = 25x²
y to the 4th power is: y⁴
3xy to the 3rd power is: (3xy)³ = 3³ x³ y³ = 27 x³ y³
The product of all these expressions is:
\((-5x)^2\cdot y^4\cdot(3xy)^3=25\cdot x^2\cdot y^4\cdot27\cdot x^3\cdot y^{3}\)We have to group like factors:
\((-5x)^2\cdot y^4\cdot(3xy)^3=(25\cdot27)\cdot(x^2\cdot x^3)\cdot(y^4\cdot y^{3})\)And solve
\(\begin{gathered} (-5x)^2\cdot y^4\cdot(3xy)^3=(675)\cdot(x^{2+3})\cdot(y^{4+3}) \\ (-5x)^2\cdot y^4\cdot(3xy)^3=(675)\cdot(x^5)\cdot(y^7) \end{gathered}\)Answer:
The answer is 675 x⁵ y⁷
Find the function values
f(x)=3x^2+3x-1
a. f(0)
b. f(2)
c. f(-2)
d. f(0)
e. f(2a)
Answers
Step-by-step explanation:
f(x)=3x−2 so when the variable x is replace with an actual value ( − 1 ) we get f(−1)=3(−1)−2
=−3−2
=−5
f(x) = 2x2 +6x − 8 mstjgh
Answers
0= -4+6x
-6x= -4 (Divide)
x=2/3
Please look at the photo! Thank you.

Answers
The output value of (g/f)(x) is 9x/(7x + 28).
The domain of g/f is (-∞, -4) U (-4, ∞)..
How to determine the corresponding composite function?In this exercise, we would determine the corresponding composite function of f(x) and g(x) under the given mathematical operations in simplified form as follows;
(g/f)(x) = (9/(x + 4)) ÷ 7/x
By rearranging the mathematical expression using the multiplication operation, we have the following:
(g/f)(x) = (9/(x + 4)) × x/7
(g/f)(x) = 9x/(7x + 28)
For the restrictions on the domain, we would have to equate the denominator of the rational function to zero and then evaluate as follows;
7x + 28 ≠ 0
7x ≠ -28
x ≠ -4
Domain = (-∞, -4) U (-4, ∞).
Read more on domain here: brainly.com/question/17440903
#SPJ1
I think the answer is nine but I’m not sure how to explain how I got my answer

Answers
Answer:
ur answer is right it is 9
Step-by-step explanation:
NOTE: divide the number 36 with 4 and u will get 9
GOOD JOB
Please mark as brainliest
Have a great day, be safe and healthy
Thank u
XD
Seventy-five 6th- grade students chose to watch a movie on the last day of school. This is 25% of the 6th-grade class. How many total students are in the 6th grade?
Answers
25% = 75/x
To solve for x, we can cross-multiply:
0.25x = 75
Then, we can divide both sides by 0.25:
x = 300
Therefore, there are 300 6th-grade students in total.
Please show steps:
Sally drives 7 more hours than Kyle on their vacation. Together they drive a total of 35 hours. How long did each person drive
Let number of hours Kyle drove =
Let number of hours Sally drove = 7
Answers
Kyle drove x hours
Sally drove x + 7 hours
Added together they both drove 2x + 7 hours
2x +7 = 35 hours
Subtract 7 from both sides:
2x = 28
Divide both sides by 2:
x = 14
Kyle drove 14 hours
Sally drove 21 hours
Kyle drove for 14 hours and Sally drove for 21 hours
Let number of hours Kyle drove = x
Let number of hours Sally drove = x+7
Therefore,
x + (x + 7) = 35
2x + 7 = 35
Collect like terms
2x = 35 - 7
2x = 28
x = 28/2
x = 14
Also, x + 7 = 24 + 7 = 21
Therefore, Kyle drove for 14 hours and Sally drove for 21 hours.
Read related link on:
https://brainly.com/question/24522925
How do I evaluate this double integral

Answers
Convert to polar coordinates with
\(x = r \cos(\theta)\)
\(y = r \sin(\theta)\)
so that \(x^2 + y^2 = r^2\), and the Jacobian determinant for this change of variables is
\(dx\,dy = r \, dr \, d\theta\)
D is the disk centered at the origin with radius 2; in polar coordinates, this is the set
\(D = \left\{(r, \theta) \mid 0\le\theta\le2\pi \text{ and } 0 \le r \le 2\right\}\)
Then the integral is
\(\displaystyle \iint_D (x + y + 10) \, dx \, dy = \int_0^{2\pi} \int_0^2 (r \cos(\theta) + r \sin(\theta) + 10) r \, dr \, d\theta\)
\(\displaystyle = \int_0^{2\pi} \int_0^2 (r^2 \cos(\theta) + r^2 \sin(\theta) + 10r) \, dr \, d\theta\)
\(\displaystyle = \int_0^{2\pi} \left(\frac83 (\cos(\theta) + \sin(\theta)) + 20\right) \, d\theta\)
\(\displaystyle = 20 \int_0^{2\pi} d\theta = \boxed{40\pi}\)
(since cos and sin are 2π-periodic)
a shelter had 4 spaniel puppies and 6 beagle puppies. Jack adopted 1/2 of the spaniel puppies, and carmen adopted 1/2 of the beagle puppies. who adopted more puppies? How do you know?
Answers
Answer:
If Jack adopted half of the spaniel puppies, and there are 4 spaniel puppies, that means that he adopted 2 puppies.
If Carmen adopted half of the beagle puppies, and there are 6 beagle puppies, then Carmen adopted 3 puppies. This means that Carmen adopted more puppies than Jack.
Step-by-step explanation:
1/2 of 4 = 2
1/2 of 6 = 3
Carmen adopted more puppies that is 3 and Jack adopted 2 puppies.
What is the fraction?In Mathematics, fractions are represented as a numerical value, which defines a part of a whole. A fraction can be a portion or section of any quantity out of a whole, where the whole can be any number, a specific value, or a thing.
Given that, a shelter had 4 spaniel puppies and 6 beagle puppies.
Jack adopted 1/2 of the spaniel puppies.
That is, 1/2 ×4 =2
Carmen adopted 1/2 of the beagle puppies.
That is, 1/2 ×6 =3
Therefore, Carmen adopted more puppies that is 3 and Jack adopted 2 puppies.
To learn more about the fraction visit:
brainly.com/question/1301963.
#SPJ2
51. MULTIPLE CHOICE Which of the following numbers is not prime?
(Skills Review Handbook)
A 1
B 2
C 3
D 5
Answers
Preview Activity 2.4.1. Consider the function f ( x ) = tan ( x ) , and remember that tan ( x ) = sin ( x ) cos ( x ) . What is the domain of f ? Use the quotient rule to show that one expression for f ′ ( x ) is f ′ ( x ) = cos ( x ) cos ( x ) + sin ( x ) sin ( x ) cos 2 ( x ) . What is the Fundamental Trigonometric Identity? How can this identity be used to find a simpler form for f ′ ( x ) ? Recall that sec ( x ) = 1 cos ( x ) . How can we express f ′ ( x ) in terms of the secant function? For what values of x is f ′ ( x ) defined? How does this set compare to the domain of f ?
Answers
Answer:
Step-by-step explanation:
Given the function f(x) = tan (x)
From trigonometry identity, tan (x) = sin(x)/cos(x)
f(x) = sin(x)/cos(x)
Using the quotient rule to find the derivative of the function, we will have;
f'(x) = cos (x)cos (x) - sin (x)[-sin (x)]/ cos²x
f'(x) = cos²x - sin²x/ cos²x
Divide through by cos²x
f'(x) = cos²x/cos²x + sin²x/cos²x / cos²x/cos²x
f'(x) = 1 + sin²x/cos²x / 1
f'(x) = 1 + (sin²x/cos²x)
f'(x) = 1 + tan²x
From trig identity, 1 + tan²x = sec²x
Hence, f'(x) = sec²x
Hence the expression f'(x) in terms of the secant function is sec²x
f'(x) = 1/cos²x
For the function to be defined, it means that cos²x ≠ 0
cos²x ≠ 0
cos x ≠ 0
x ≠ cos⁻¹0
x ≠ 90⁰
Hence the value of x must not be equal to 90 for the function to be defined. x can be defined at when x = 0 since cos 0 = 1, the equation will becomes f'(0) = 1/cos²0 = 1/1 = 1.
Hence the function is defined at 0≤x<90
Can anyone help me answer this question?
f(x) = 5x^3 + 3x^2 - x/ x+2 and g(x) = x^2 - 1/ x - 1. Find the limit of f^2(x) as x approaches 2
Answers
The function limit of f(x) as x approaches 2 is 67 and the limit of f²(x) as x approaches 2 is 4489.
The function f(x) can be rewritten as:
f(x) = (5x³ + 3x² - x)/(x+2)
Using direct substitution, we see that f(2) is undefined, as the denominator of the function becomes 0.
To evaluate the limit, we can use L'Hopital's rule:
\(\lim_{x \to 2\\) f(x) = lim x→2 (5x³ + 3x² - x)/(x+2)
= \(\lim_{x \to 2\\) (15x² + 6x - 1)/(1)
= (15(2)² + 6(2) - 1)/(1)
= 67
To find the limit of f²(x) as x approaches 2, we can simply square the limit:
f(x) = \(\lim_{x \to 2\}\)f²(x)
= \(\lim_{x \to 2\) f²(x)
= 67²
= 4489
To learn more about function follow the link:
https://brainly.com/question/28971475
#SPJ1
The total for parking and an admission ticket
Answers
Answer:
Step-by-step explanation:
n+n
Answer:
n+n
Step-by-step explanation:
I think thats right
PLEASEEEE HELP! MY MOM IS GONNA KILL ME

Answers
Answer:
16
Step-by-step explanation:
Since the perimeter of the rectangle is 80, we can set up the perimeter formula:
80=2L+2W=2(3x+3)+2(2x+2)=6x+6+4x+4=10x+10
10x=70
x=7
AB=2x+2=2(7)+2=14+2=16
Answer:
AB= 16
Step-by-step explanation:
2x+2+3x+3=40
Add like terms: 2x+3x= 5x and 2+3=5
New equation: 5x+5=40
Solve: 40-5= 35
35 divided by 5= 7Now we know that x is equal to 7.
2(7)+2= 16
Side DC equals 16.
Side AB has the same length as side DC since it's a rectangle.
Side AB equals 16.
Let's check: 16+16=32 (side DC and side AB)
80-32=483(7)+3= 2424 must be the length of the other sides.
24+24= 48So, when you add all the sides together...
16+16+24+24= 80
You get 80, the perimeter!
I hope this helped!
Evaluate the estimate slope of f(x)= x 2 +1 (i) x=1 (ii) x= 2
pls guys help me i need the answer fast please
Answers
i.2
ii.4
Step-by-step explanation:
to estimate a slope simply means to differentiate,
from the equation:f(x)=x^2+1
dx/dy=2x+0=2x
where x=1
it becomes:2(1)=2
where x=2
it becomes:2(2)=4
Write the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 in this order and insert '+' or '-' between them to get the result 3? Please Help
Answers
Answer:
0 - 1 - 2 + 3 - 4 + 5 - 6 +7 - 8 + 9 = 3
Step-by-step explanation:
8(15-4)
----------
4²-5
Answers
Step-by-step explanation:
8(15-4)
----------
4square - 5
= 8(15-4)
=120 - 32
= 88
4square - 5
=4×4 = 16
16 - 5
= 11
therefore,
88/11
= 8
Increase £50 by 60% anyone can help me?
Answers
so the answer is 80
4. A plumber charges $45 per hour plus a $25 service charge. If a represents his total charges in dollars and b represents
the number of hours worked, which formula below could the plumber use to calculate his total charges? (A-CED.1)
A. a = 45 + 25b
B. a = 45 + 25 +b
C. a = 45b + 25
D. a = (45) (25) + b
Answers
Answer:
C. a=45b + 25
Step-by-step explanation:
Answer:
It would be C
Step-by-step explanation:
a = 45b + 25
Reason:
It says the plumber charges 45 dollars per hour and that b is the number of hours worked. so we multiply 45 dollars by the variable b(number of hours worked), then we add the service charge, since the service charge is only added once, we do not multiply it by a variable.
Therefore we get:
a = 45b + 25
The function f(t) = 3 cos(pi over 6t) + 5 represents the tide in Blastic Sea. It has a maximum of 8 feet when time (t) is 0 and a minimum of 2 feet. The sea repeats this cycle every 12 hours. After nine hours, how high is the tide? 12 feet 5 feet 4.5 feet 2.5 feet
Answers
Answer:
5 feet
Step-by-step explanation:
\(f(t) = 3 cos \bigg( \frac{\pi}{6} t\bigg) + 5 \\ \\ plug \: t = 9 \\ \\ \implies \: f(9) = 3 cos \bigg( \frac{\pi}{6} \times 9 \bigg) + 5 \\ \\\implies \: f(9) = 3 cos \bigg( \frac{3\pi}{2}\bigg) + 5 \\ \\\implies \: f(9) = 3 cos \bigg( \pi + \frac{\pi}{2}\bigg) + 5 \\ \\\implies \: f(9) = - 3 cos \bigg( \frac{\pi}{2}\bigg) + 5 \\ [ \because \: cos ({\pi}+\theta) = -\cos \theta]\\\\\implies \: f(9) = - 3 (0) + 5 \\ ( \because \: cos \frac{\pi}{2} = 0) \\ \\ \implies \: f(9) = 0 + 5 \\ \\ \implies \: \huge{ \orange{f(9) = 5 }}\)
A hospital needs a supply of an expensive medicine. Company A has the most supply available, 1.7 milligrams, which is twice
the difference between the weight of Company B's supply and Company C's, and 0.9 milligram more than Company C's supply.How many milligrams can the hospital get from these three companies?
Answers
The hospital can get 4.15 milligrams from these three companies.
A linear equation is one in which the highest power of any variable is not more than 1. A linear equation in 2 variables can be solved by substitution method, if we have two simultaneous equations.
Here, we know that
Company A's supply of medicine = 1.7 mg
also, company A's supply = 2( B's supply - C's supply)
⇒ 1.7 = 2( B - C)
⇒ 1.7 = 2B - 2C .... (1)
Moreover, we are given that
A's supply = C's supply + 0.9
⇒ 1.7 = C + 0.9
⇒ 1.7 - 0.9 = C
⇒ 0.8 = C
Now, substituting the value of C in (1), we get,
1.7 = 2B - 2(0.8)
1.7 = 2B - 1.6
1.7 + 1.6 = 2B
⇒ B = 3.3/2
B = 1.65
Thus, the total supply from all three companies is (1.7 + 1.65 + 0.8) = 4.15 mg
Learn more about Linear equations here-
https://brainly.com/question/13729904
#SPJ9
People use water to cook, clean, and drink every day. An estimate of 22.7% of the water used each day is for cooking. If a family uses 68.1 gallons of water a day for cooking, how many gallons do they use every day?
Answers
We know that 22.7% of this amount is used for cooking,the family uses 300.001 gallons of water every day.
What is gallons?
Gallon is a unit of measurement used to quantify liquid volume in both the US customary and British imperial systems of measurement.
Let's start by using algebra to solve the problem.
Let x be the total amount of water the family uses every day. We know that 22.7% of this amount is used for cooking, which means:
0.227x = 68.1
To solve for x, we can divide both sides of the equation by 0.227:
x = 68.1 ÷ 0.227
x = 300.001 (rounded to three decimal places)
Therefore, the family uses 300.001 gallons of water every day.
To know more about equation visit:
brainly.com/question/28874341
#SPJ1
Here is a sample distribution of hourly earnings in Paul's Cookie Factory:
Hourly Earning $6 up to $9 $9 up to $12 $12 up to $15
Frequency 16 42 10
The limits of the class with the smallest frequency are:_________
A) $6.00 and $9.00.
B) $12.00 and up to $14.00.
C) $11.75 and $14.25.
D) $12.00 and up to $15.00.
Answers
Answer:
The correct answer is:
$12.00 and up to $15.00 (D)
Step-by-step explanation:
Let us arrange the data properly in a tabular format.
Hourly Earnings($) 6 - 9 9 - 12 12 - 15
Frequency 16 42 10
The frequency of a distribution is the number of times that distribution occurs in a particular group of data or intervals.
From the frequency table above the following observations can be made:
Highest frequency = 42 (hourly earnings of $9 - $12)
smallest frequency = 10 ( hourly earnings of $12 - $15)
This means that among a total of 68 workers (16 + 42 + 10), the people earning $12 - $15 form the smallest group (only 10 people), while 42 workers earn $9 - $12, forming the largest majority
Which statements are true? Select each correct answer. Responses Only some triangles are plane figures. Only some triangles are plane figures. All triangles are polygons. All triangles are polygons. All triangles have 3 right angles. All triangles have 3 right angles. All triangles are closed figures. All triangles are closed figures. All triangles have 3 straight sides.
Answers
The three true statements are as follows:
All triangles are polygons.All triangles are closed figures. All triangles have 3 straight sides.What are the true statements?In the list, there are several true statements and some of them include the facts that all triangles are polygons, they are closed figures and they have three straight sides.
A polygon is a shape with two or more sides. Triangles ahve three sides, so we can easily address them as polygons. Also, all triangles are closed figures and they also have three straight sides.
Learn more about triangles here:
https://brainly.com/question/17335144
#SPJ1
You select three cards from a deck of cards without replacement. The first card is a king, then queen, and lastly a jack. What is the probability you select those three cards in that order? Round answer to nearest hundredth and include percent sign.
Answers
equivalent expression for
100x14
\(14(10)\)
\(361 \times 1000\)
\(100(361)\)
Answers
\(\huge\bold{ANSWER:}\)
\(\huge\bold{1,400} ~and~\huge\bold{361,000}\)
\(\huge\bold{SOLUTION:}\)
\(\huge\mathrm{100*14}\)
Multiply:
\(\huge\mathrm{1,400}\) (Answer)
\(\huge\mathrm{361*1,000}\)
Multiply:
\(\huge\mathrm{361,000}\)
_______________________________________
Additional Note:
\(\bigstar\) If we multiply by 100, we add 2 zeros.
Example: \(\bold{\underline{14*100=1,400}}\)
\(\bigstar\) If we multiply by 1,000, we add 3 zeros.
Example: \(\bold{\underline{361*1,000=361,000}}\)
______________________________________
Hope you find it helpful.
Feel free to ask if you have any doubts.
\(\bold{-MistySparkles^**^*}\)
Find the area of the shape shown below.
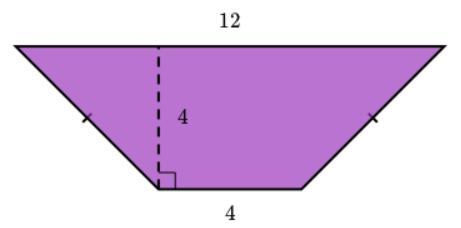
Answers
Answer:
The answer is 32
Step-by-step explanation:
The formula for finding the area of a trapezoid is:
((base 1 + base 2)/ 2 )* h
Now all you have to do is substitute the numbers in.
Note: bases will always be the ones like 12 and 4 in this case. We have just named then 1 and 2.
Answer:
32 square units
Step-by-step explanation:
\(\displaystyle A=\frac{1}{2}(b_1+b_2)h=\frac{1}{2}(12+4)(4)=\frac{1}{2}(16)(4)=\frac{1}{2}(64)=32\)
Note that \(b_1\) and \(b_2\) are the lengths of each base of the trapezoid, so it doesn't matter which is which.
