Find the largest number δ such that if |x − 1| < δ, then |2x − 2| < ε, where ε = 1.
δ ≤
Repeat and determine δ with ε = 0.1.
δ ≤

Answer:

The answer is 90 degrees

Step-by-step explanation:

We know that a circle is 360 degrees. 1/4 of that is 90

The derivative of the cross product u(t) × v(t) with respect to t is given by:

d/dt [u(t) × v(t)] = [d/dt u(t)] × v(t) + u(t) × [d/dt v(t)]

Using the given functions, we have:

d/dt [u(t) × v(t)] = [leftangle0.gif 8cos(8t), 8sin(8t), 1 rightangle0.gif] × [t, cos(8t), sin(8t)] + [sin(8t), cos(8t), t] × [leftangle0.gif -8sin(8t), 8cos(8t), 0 rightangle0.gif]

Simplifying this expression, we get:

d/dt [u(t) × v(t)] = [8t, -8sin^2(8t), 8cos^2(8t)] + [8sin(8t), 8cos^2(8t), -8sin^2(8t)]

Therefore, the derivative of the cross product is:

d/dt [u(t) × v(t)] = [8t + 8sin(8t), 8cos^2(8t) - 8sin^2(8t), 8cos^2(8t) - 8sin^2(8t)]

To learn more about cross product, here

https://brainly.com/question/29164170

#SPJ4

Given, dy/dt = y²(5 - y²)We can find the critical points as follows,dy/dt = 0y²(5 - y²) = 0y² = 0 or (5 - y²) = 0y = 0 or y = ±√5The critical points are (0, 0), (- √5, 0) and (√5, 0).The sign of dy/dt can be evaluated for each of these points,For (- √5, 0), dy/dt = (- √5)²(5 - (- √5)²) = -5√5 which is negative. Hence, the point is semistable.For (0, 0), dy/dt = 0 which means that the point is an equilibrium point.For (√5, 0), dy/dt = (√5)²(5 - (√5)²) = 5√5 which is positive. Hence, the point is unstable.

(- √√5,0) is semistable, (0, 0) is asymptotically stable, (√5,0), is unstable.There are a few types of equilibrium points such as asymptotically stable, unstable, and semistable. In this problem, we need to classify the critical (equilibrium) points as asymptotically stable, unstable, or semistable.The critical points are the points on the graph where the derivative is zero. Here, we have three critical points: (0, 0), (- √5, 0) and (√5, 0).

To classify these critical points, we need to evaluate the sign of the derivative for each point. If the derivative is positive, then the point is unstable. If the derivative is negative, then the point is stable. If the derivative is zero, then further analysis is needed.To determine if the point is asymptotically stable, we need to analyze the behavior of the solution as t approaches infinity. If the solution approaches the critical point as t approaches infinity, then the point is asymptotically stable. If the solution does not approach the critical point, then the point is not asymptotically stable.For (- √5, 0), dy/dt is negative which means that the point is semistable.For (0, 0), dy/dt is zero which means that the point is an equilibrium point.

To determine if it is asymptotically stable, we need to do further analysis.For (√5, 0), dy/dt is positive which means that the point is unstable. Therefore, the answer is (- √√5,0) is semistable, (0, 0) is asymptotically stable, (√5,0), is unstable.

To know more about critical points Visit

https://brainly.com/question/7805334

#SPJ11

The volume of the given rectangular prism is 13.5 units³

Given that the area of the base of a rectangular prism is 27/5 units², and the height is 5/2 units, we need to find the volume,

Volume = base area x height

= 27/5 x 5/2

= 13.5

Hence, the volume of the given rectangular prism is 13.5 units³

Learn more about rectangular prism click;

https://brainly.com/question/21308574

#SPJ1

Answer:

The answer is A. Both 1 and 4

Step-by-step explanation:

Answer:

20x+50......

and 10(2x+5)

To calculate the product of two random variables that follows the normal distribution with mean 0 and variance 1 by using the covariance formula

Cov(X, Y) = E[XY] - E[X]E[Y] = E[XY] - 0 = E[XY]

Given that two random variables follow a normal distribution with mean 0 and variance 1.

Let X and Y be two independent normal random variables such that X ~ N(0,1) and Y ~ N(0,1)

Now, The expected value of the product of two random variables is given by;

E[XY] = E[X]E[Y] + Cov(X,Y)

Where E[X] and E[Y] are the means of the two random variables X and Y respectively.

Cov(X, Y) is the covariance between the two random variables, which can be calculated using the formula;

Cov(X,Y) = E[XY] - E[X]E[Y]

Now, E[X] = E[Y] = 0 as both have a mean of 0.

Cov(X, Y) = E[XY] - E[X]E[Y]

⇒ E[XY] = the expected value of the product of X and Y.

As X and Y are independent, their covariance will be zero, which implies;

Cov(X, Y) = E[XY] - E[X]E[Y] = E[XY] - 0 = E[XY]

Thus, we can calculate the product of two random variables that follow a normal distribution with mean 0 and variance 1 using the above formula for covariance.

To know more about the "covariance": https://brainly.com/question/21287720

#SPJ11

The width and height of the model are;

Width of model = 13.5 inches

Height of model = 2.25 inches

A scale model is defined as a physical model that is geometrically similar to an object. Scale models are usually smaller than large prototypes such as vehicles, buildings, or people. However, these scale models may be larger than small prototypes such as anatomical structures or subatomic particles.

Now, we are given that the dimensions of the new medical complex are;

Length = 400 ft

Width = 180 ft

Height = 40 ft

Thus, for a scale model with length of 30 in(2.5 ft) long, the scale factor is; Scale factor = 2.5/400

Thus;

Width of model = 180 * (2.5/400)

= 1.125 ft = 13.5 inches

Height = 30 * (2.5/400)

= 0.1875 ft = 2.25 inches

Read more about Scale Model at; https://brainly.com/question/261465

#SPJ1

Answer: Part A is (-9, 13) Part B is (9, 13)

Step-by-step explanation:

In a coordinate system, a vector is oriented at an angle this statement is false.

In a coordinate system, vectors are typically represented by their components along the coordinate axis . These components determine the direction and magnitude of the vector. The orientation of a vector is determined by the angles it makes with the coordinate axis or by the direction cosines or direction angles that specify its direction in space.

The direction of a vector can be represented using angles, such as the azimuthal angle (horizontal angle) and inclination angle (vertical angle) in spherical coordinates or the angles of inclination from the positive x-axis and positive z-axis in cylindrical coordinates.

Therefore, it is incorrect to say that a vector is oriented at an angle in a coordinate system. The orientation of a vector is defined by its components or direction angles relative to the coordinate axis.

learn more about vector :

https://brainly.com/question/30958460

#SPJ4

True. In a coordinate system, a vector can be oriented at any angle with respect to the reference axis.

In a coordinate system, a vector can be oriented at any angle with respect to the reference axis. The angle at which a vector is oriented is measured with respect to a reference axis, usually the positive x-axis. This angle is typically measured in degrees or radians.

The orientation of a vector can be described using trigonometric functions such as sine, cosine, and tangent. These functions relate the angle of orientation to the coordinates of the vector in the coordinate system. For example, the x-coordinate of a vector can be determined using the cosine function, while the y-coordinate can be determined using the sine function.

The orientation of a vector can also be represented using direction angles. In two-dimensional space, the orientation of a vector can be described using a single angle. In three-dimensional space, the orientation of a vector can be described using direction angles, which are the angles between the vector and each of the coordinate axes.

About coordinate system here:

https://brainly.com/question/4726772

#SPJ11

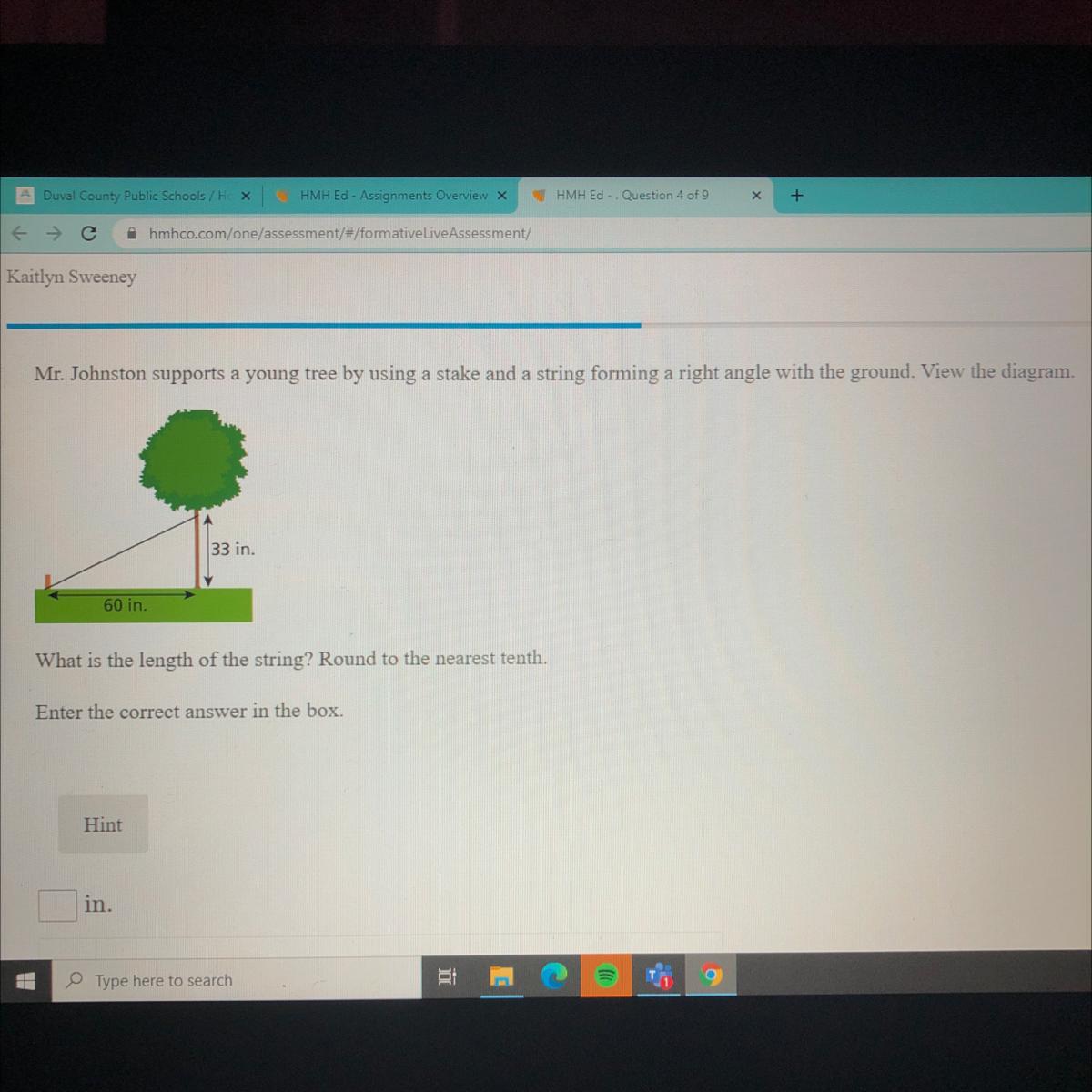
Answer:

Step-by-step explanation:

10 inches

Answer:

68.5 inches

Step-by-step explanation:

The pythagorean theorem is a^2+b^2 = c^2

In this case, a = 60, b = 33, and we are looking for c, so this is how you do it:

60^2 + 33^2 = 3600 + 1089 = 4689

sqrt(4689) = 68.47627326...

Rounded to the nearest tenth is 68.5!

Answer: B (The cost of a notebook is $0.75, and the cost of a folder is $0.25.)

Step-by-step explanation:

No need for explanation. i know i’m right!!

The minimal value of s = x^2 y^2 is 5/3, and it is achieved when:
x = ±(3/5)^(1/2)
y = ±(2/5)^(1/2)

To solve this problem, we can use the method of Lagrange multipliers. Let's define the Lagrangian function L(x,y,λ) as follows:
L(x,y,λ) = x^2 y^2 + λ(3x + 4y - 25)

where λ is the Lagrange multiplier.

To find the minimal value of s = x^2 y^2, we need to solve the following system of equations:
∂L/∂x = 2xy^2 + 3λ = 0
∂L/∂y = 2x^2y + 4λ = 0
∂L/∂λ = 3x + 4y - 25 = 0

Solving the first two equations for x and y, we get:
x = -3λ/2y^2
y = -2λ/4x^2

Substituting these expressions into the third equation, we get:
3(-3λ/2y^2) + 4(-2λ/4x^2) - 25 = 0

Simplifying this equation, we get:
-9λ/y^2 - 2λ/x^2 - 25 = 0

Multiplying both sides by x^2 y^2, we get:
-9λx^2 - 2λy^2 + 25x^2 y^2 = 0

Dividing both sides by λ, we get:
-9x^2/y^2 - 2y^2/x^2 + 25x^2 y^2/λ^2 = 0

This equation can be simplified to:
-9x^4 - 2y^4 + 25s/λ^2 = 0

where s = x^2 y^2.

We can now solve for λ in terms of s:
λ^2 = 25s/(9x^4 + 2y^4)

Substituting this expression for λ into the equations for x and y, we get:
x = ±(3s/5)^(1/4)
y = ±(2s/5)^(1/4)

Note that we have four possible solutions, corresponding to the four possible combinations of signs for x and y.

To find the minimal value of s, we need to evaluate s for each of these solutions and choose the smallest one. We get:

s = x^2 y^2 = (3s/5)^(1/2) (2s/5)^(1/2) = (6s/25)^(1/2)

This equation can be simplified to:
s = 5/3

Therefore, the minimal value of s = x^2 y^2 is 5/3, and it is achieved when:
x = ±(3/5)^(1/2)
y = ±(2/5)^(1/2)

Note that these values satisfy the constraint equation 3x + 4y - 25 = 0.

Know more about minimal value here:

https://brainly.com/question/30236354

#SPJ11

The value of k from the equation is k = -20

The equation of a line is expressed as y = mx + b where m is the slope and b is the y-intercept

And y - y₁ = m ( x - x₁ )

y = y-coordinate of second point

y₁ = y-coordinate of point one

m = slope

x = x-coordinate of second point

x₁ = x-coordinate of point one

The slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )

Given data ,

Let the equation of line be represented as A

Now , the value of A is

y = kx   be equation (1)

Let the first point be P ( 4 , -80 )

Substituting the values in the equation , we get

-80 = 4k

Divide by 4 on both sides of the equation , we get

k = - ( 80/4 )

On simplifying the equation , we get

k = -20

Hence , the equation is k = -20

To learn more about equation of line click :

https://brainly.com/question/14200719

#SPJ1

Each transformation affects the shape and position of the graph. It is important to carefully consider the order of the transformations and their impact on the equation.

1. Horizontal Shift (c):
If there is a horizontal shift, the equation becomes y = (x - c)^3.
For example, if there is a shift of 2 units to the right, the equation would be y = (x - 2)^3.

2. Vertical Shift (d):
If there is a vertical shift, the equation becomes y = x^3 + d.
For example, if there is a shift of 3 units upwards, the equation would be y = x^3 + 3.

3. Vertical Stretch (a):
If there is a vertical stretch or compression, the equation becomes y = a * x^3.
For example, if there is a vertical stretch by a factor of 2, the equation would be y = 2 * x^3.

4. Reflection (along the x-axis):
If there is a reflection along the x-axis, the equation becomes y = -x^3.
This flips the graph of the original function upside down.

5. Reflection (along the y-axis):
If there is a reflection along the y-axis, the equation becomes y = (-x)^3.
This mirrors the graph of the original function.

6. Combined Transformations:
If there are multiple transformations, we can apply them in the order they are given. For example, if there is a vertical stretch by a factor of 2 and a horizontal shift of 3 units to the right, the equation would be y = 2 * (x - 3)^3.

Remember, each transformation affects the shape and position of the graph. It is important to carefully consider the order of the transformations and their impact on the equation.

To know more about equation here:

brainly.com/question/29292690

#SPJ11

a. The composite function f(g(x)) is given by f(g(x)) = 5a^2 + 18a + 12.

b. The composite function f(g(x)) is given by f(g(x)) = 5x^2 + (10h - 2)x + (5h^2 - 2h - 4).

a. To find f(g(x)), we need to substitute g(x) into the function f(a). Given that g(x) = a + 2, we can substitute a + 2 in place of a in the function f(a):

f(g(x)) = f(a + 2)

Now, let's substitute this expression into the function f(a):

f(g(x)) = 5(a + 2)^2 - 2(a + 2) - 4

Expanding and simplifying:

f(g(x)) = 5(a^2 + 4a + 4) - 2a - 4 - 4

f(g(x)) = 5a^2 + 20a + 20 - 2a - 4 - 4

Combining like terms:

f(g(x)) = 5a^2 + 18a + 12

Therefore, the composite function f(g(x)) is given by f(g(x)) = 5a^2 + 18a + 12.

b. Similarly, to find f(g(x)), we substitute g(x) into the function f(a). Given that g(x) = x + h, we can substitute x + h in place of a in the function f(a):

f(g(x)) = f(x + h)

Now, let's substitute this expression into the function f(a):

f(g(x)) = 5(x + h)^2 - 2(x + h) - 4

Expanding and simplifying:

f(g(x)) = 5(x^2 + 2hx + h^2) - 2x - 2h - 4

f(g(x)) = 5x^2 + 10hx + 5h^2 - 2x - 2h - 4

Combining like terms:

f(g(x)) = 5x^2 + (10h - 2)x + (5h^2 - 2h - 4)

Therefore, the composite function f(g(x)) is given by f(g(x)) = 5x^2 + (10h - 2)x + (5h^2 - 2h - 4).

To know more about expression, visit

https://brainly.com/question/28170201

#SPJ11

In a simple linear regression model, the coefficient of the independent variable (x) in the estimated sample regression equation indicates the change in the predicted value of the dependent variable (y) when x increases by one unit. This coefficient is also known as the slope of the regression line. Therefore, to calculate the predicted value of y, we multiply the coefficient by the value of x and add the intercept.

In a simple linear regression model, the coefficient that indicates the change in the predicted value of y when x increases by one unit is the "slope coefficient" or the "regression coefficient" (usually denoted as b1). This coefficient represents the relationship between the independent variable x and the dependent variable y.

The linear regression equation is given as:

y = b0 + b1 * x

Where:
- y is the predicted value of the dependent variable
- b0 is the intercept coefficient (where the line intersects the y-axis)
- b1 is the slope coefficient (the change in y when x increases by one unit)
- x is the independent variable

In this equation, b1 indicates the change in the predicted value of y when x increases by one unit.

visit here to learn more about linear regression:

brainly.com/question/29665935

#SPJ11

Using the empirical rule, about 99.7% of the scores lie between 75 to 93

In this question, we have been given ms. wilson's science test scores are normally distributed with a mean score of 84 (μ) and a standard deviation of 3 (σ).

We know that the empirical rule predicts that 99.7% within the first three standard deviations (µ ± 3σ).

An empirical rule is also known as 68-95-99.7 rule.

We find the interval (µ ± 3σ)

The upper value would be,

µ + 3σ

= 84 + 3(3)

= 84 + 9

= 93

and the lower value would be,

µ - 3σ

= 84 - 3(3)

= 84 - 9

= 75

Therefore, about 99.7% of the scores lie between (75, 93)

Learn more about 68-95-99.7 rule  here:

https://brainly.com/question/16012911

#SPJ4

Hey there!

The answer to your question is 142

This is because they are vertical angles, and that means that are equal.

Have a good day!

Answer:

∠x=142°

Step-by-step explanation:

line properties use angle 142 and angle x° vertical angle.

\(\angle x^{o}=142^{o}\)

Hope this helps!

Answer:

2.50 dollars.

Step-by-step explanation:

Answer:

ur welcoem

Step-by-step explanation:

Answer:

6^2

Step-by-step explanation:

Answer:

6 ** 2

Step-by-step explanation:

becuase you can't use ^ in python you use ** to square.

The integer that can be  inserted on the blank line in the list is: -2

The number line is given as:

-15, -3, ____, -1.5, 2, 3, 5

Now, a number line is defined as a line on which numbers are marked at intervals, used to illustrate simple numerical operations.

In this case, we see that the interval of the number line is from -15 to 5.

Thus, the range of values for the blank space will fall in between those two numbers.

Now, since we have positive 2 on the number line, then we must likely also have the negative one to balance it as the blank number.

Read more about Number Line at: https://brainly.com/question/24644930

#SPJ1

Answer:

\(\frac{dy}{dx} = \frac{13}{8} \)

Step-by-step explanation:

\( y = 2x + 6 {x}^{ - \frac{1}{2} } \\ \frac{dy}{dx} = 2 + 6( - \frac{1}{2}) {x}^{ - \frac{1}{2} - 1 } \\ \frac{dy}{dx} = 2 - 3 {x}^{ - \frac{3}{2} } \\ \frac{dy}{dx} = 2 - \frac{3}{ \sqrt{ {x}^{3} } } \)

When x = 4,

\(\frac{dy}{dx} = 2 - \frac{3}{ \sqrt{ {4}^{3} } } \\ = \frac{13}{8} \)

Answer:

Hello,

Answer 13/8

Step-by-step explanation:

\(y=2x+\dfrac{3}{\sqrt{x} } \\\\y'=2+6*\dfrac{-1}{2} x^{\frac{-3}{2} }\\\\y'=3-\frac{3}{\sqrt{x^3}} \\\\\\For x=4, \\\\y'(4)=2-\dfrac{3}{8} =\dfrac{13}{8}\)

Answer: The diameter is 12ft.

Step-by-step explanation:

The length of the rope will be equal to the perimeter of the trampoline.

We know that the trampoline is circular, so the perimeter of a circle can be written as

P = 2*pi*r

where r is the radius, and pi = 3.14...

Then we now should find the perimeter.

if 1ft of rope costs $2.75

now, how many times we can fit $2.75 in $104.50?

We look at the quotient

$104.50/$2.75 = 38

So 38 times, this means that the full rope is 38 times 1 ft, or 38 ft long.

Then the perimeter of the circle is 38ft.

P = 38ft = 2*3.14*r

Now we can find the value of the radius:

r = 38ft/(2*3.14) = 6.05 ft

Now, we want to find the diameter, and we know that the diameter is two times the radius, then:

d = 2*r = 2*(6.05ft) = 12.1 ft.

But we want this to the nearest foot, so we should round it down to 12ft.

The diameter is 12ft.

Answer:

I am pretty sur it is 3

Step-by-step explanation:

Answer:

3f

Step-by-step explanation:

The expression given is f + f + f.

f + f + f = f × 3

The correct way to write an expression that is being multiplied is to put the number before it with no symbols or spaces in between them:

f + f + f =

f × 3 =

3f

A) Function is increasing on (-∞, -1) and (7/2, ∞), and decreasing on (-1, 7/2).

b)  The local minimum value of f is; 5608/2197 at x = -42/13, and the local maximum value of f is 139/8 at x = 7/2.

(a) To determine the intervals on which f is increasing or decreasing, we need to determine the critical points and then check the sign of the derivative on the intervals between them.

f(x)=8x³-42x-48x + 4

f'(x) = 24x² - 90

Setting f'(x) = 0, we get

24x² - 90 = 0

24x² = 90

x =±  √3.75

So, the critical points are;

x = -1 and x = 7/2.

We can test the sign of f'(x) on the intervals as; (-∞, -1), (-1, 7/2), and (7/2, ∞).

f'(-2) = 72 > 0, so f is increasing on (-∞, -1).

f'(-1/2) = -25 < 0, so f is decreasing on (-1, 7/2).

f'(4) = 72 > 0, so f is increasing on (7/2, ∞).

Therefore, f is increasing on (-∞, -1) and (7/2, ∞), and decreasing on (-1, 7/2).

(b) To determine the local maximum and minimum values of f, we need to look at the critical points and the endpoints of the interval (-1, 7/2).

f(-1) = -49

f(7/2) = 139/8

f(-42/13) = 5608/2197

Learn more about maximum value  here:

brainly.com/question/23504923

#SPJ4

Answer:

I can't see the graph anywhere.

Step-by-step explanation:

Step-by-step explanation:

in the figure angle s= angle c

so according to the rule of congruent and similarity

dc=Sr

Answer:

A

Step-by-step explanation:

Answer:

it would be d

Step-by-step explanation:

16 times 8 3/4