Find the image of the given point
under the given translation.
P(-9, -2)
T(x, y) = (x + 6, y − 4)
P' = ([?], [])
![Find The Image Of The Given Pointunder The Given Translation.P(-9, -2)T(x, Y) = (x + 6, Y 4)P' = ([?],](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/ZOaExSHj8ccNx9xwMYOZZW9k4DPSKbJo.png)
Answers
Explanation:
The notation \(T(x, y) = (x+6, y-4)\) tells us to add 6 to the x coordinate and subtract 4 from the y coordinate.
An equivalent notation would be to write \((x,y) \to (x+6, y-4)\)
Point P has the x coordinate of -9. Adding on 6 gets us the new x coordinate of -9+6 = -3
It also has the y coordinate of -2. Subtract off 4 to get -2-4 = -6
So,
\((x,y) \to (x+6, y-4)\\\\(-9, -2) \to (-9+6, -2-4)\\\\(-9, -2) \to (-3, -6)\)
Answer:
P' (- 3, - 6 )
Step-by-step explanation:
the translation
(x, y ) → (x + 6, y - 4 )
means add 6 to the x- coordinate and subtract 4 from the y- coordinate , so
P (- 9, - 2 ) → P' (- 9 + 6, - 2 - 4 ) → P' (- 3, - 6 )
Related Questions
where does the line cross the y axis on the line y=-3x+15
Answers
Answer: 15
Step-by-step explanation: in y=mx+b B= the y-intercept aka where the line touches the y axis
Answer:
Y= 15 or (0,15) that is the answer, hope it's not to late
Let f: C\ {0} → C be a holomorphic function such that
f(z) = f (1/z)
for every z £ C\ {0}. If f(z) £ R for every z £ OD(0; 1), show that f(z) £ R for every Z£R\ {0}. Hint: Schwarz reflection principle may be useful.
Answers
The function f(z) = f(1/z) for every z ∈ ℂ{0} implies that f(z) is symmetric with respect to the unit circle. Since f(z) ∈ ℝ for z ∈ OD(0; 1), we can extend this symmetry to the real axis and conclude that f(z) ∈ ℝ for z ∈ ℝ{0}.
Consider the function g(z) = f(z) - f(1/z). From the given condition, we have g(z) = 0 for every z ∈ ℂ{0}. We can show that g(z) is an entire function. Let's denote the Laurent series expansion of g(z) around z = 0 as g(z) = ∑(n=-∞ to ∞) aₙzⁿ.
Since g(z) = 0 for every z ∈ ℂ{0}, we have aₙ = 0 for every n < 0, since the Laurent series expansion around z = 0 does not contain negative powers of z. Therefore, g(z) = ∑(n=0 to ∞) aₙzⁿ.
Now, let's consider the function h(z) = g(z) - g(1/z). We can observe that h(z) is also an entire function, and h(z) = 0 for every z ∈ ℂ{0}. By the Identity Theorem for holomorphic functions, since h(z) = 0 for infinitely many points in ℂ{0}, h(z) = 0 for every z ∈ ℂ{0}. Thus, g(z) = g(1/z) for every z ∈ ℂ{0}.
Now, let's focus on the real axis. For z ∈ ℝ{0}, we have z = 1/z, which implies g(z) = g(1/z). Since g(z) = f(z) - f(1/z) and g(1/z) = f(1/z) - f(z), we obtain f(z) = f(1/z) for every z ∈ ℝ{0}. This means that f(z) is symmetric with respect to the real axis.
Since f(z) is symmetric with respect to the unit circle and the real axis, and we know that f(z) ∈ ℝ for z ∈ OD(0; 1), we can conclude that f(z) ∈ ℝ for every z ∈ ℝ{0}.
To know more about symmetric , refer here:
https://brainly.com/question/31184447#
#SPJ11
If the forecast for two consecutive periods is 1,500 and 1,400 and the actual demand is 1,200 and 1,500 , then the mean absolute deviation is 1) 500 2) 700 3) 200 4) 100
Answers
200 is the mean absolute deviation. Therefore, choice three (200) is the right one.
How to calculate the mean absolute deviation
The absolute difference between the predicted and actual values must be determined, added together, and divided by the total number of periods.
Forecasted values are as follows: 1,500 and 1,400
Values in actuality: 1,200 and 1,500
Absolute differences:
|1,500 - 1,200| = 300
|1,400 - 1,500| = 100
Now, we calculate the MAD:
MAD = (300 + 100) / 2 = 400 / 2 = 200
Therefore, 200 is the mean absolute deviation. Therefore, choice three (200) is the right one.
Learn more about mean absolute here :brainly.com/question/29545538
#SPJ4
How many rows and columns are in this table?

Answers
Answer:
There are five rows and ten columns
Answer:
5 rows and 10 columns i think
Step-by-step explanation:
What is the ?, help please

Answers
Step-by-step explanation:
According to the base of similarity, then
12÷6=8÷x
12x=48
=4
6+4=
10
Ron went to the store with $100.00. He bought 2 belts for $14.00 each, he bought 3 shirts for $15.00 each, and he bought a pair of jeans for $25. How much money did he have left? Choose the correct solution
$1.00
$10.00
$4.00
$2.00
Answers
Answer:
2 dollars
Step-by-step explanation:
if you add all the numbers and subtract them by 100 you left with 2
find the length of the arc travelled by the 4-inch long minute hand of a clock when moving from 1:30pm to 2:15pm
Answers
Answer:
18.8 inches
Step-by-step explanation:
You want the length of arc traveled by the tip of a 4" minute hand moving from 1:30 pm to 2:15 pm.
ArcThe time difference between 2:15 and 1:30 is 45 minutes, or 3/4 hour. The minute hand moves through an angle of 2π radians in 1 hour, so will move through an angle of (3/4)(2π) = 3/2π radians in 3/4 hour.
LengthThe length of an arc is given by the formula ...
s = rθ
where r is the radius, and θ is the central angle in radians.
Here, we have r = 4 in, and θ = 3π/2. The arc length is ...
s = (4 in)(3π/2) = 6π in ≈ 18.8496 in
The minute hand moves through an arc of about 18.8 inches from 1:30 to 2:15.
Omar has a goal of walking 9,000 steps in one day. He has already walked 4,250 steps. You want to know how many more steps he needs to take. If you use the equation n+4,250=9,000 to solve this problem, what does n represent?
Answers
Answer:
n=4750
n+ 4250=9000
-4250= 4250
n= 4750
Answer:
Step-by-step explanation:
idea
The money collected from a Saturday car wash are directly proportional to the number of cars washed. The total money collected after 7 cars is $140. Write an direct variation equation relating the money collected (m) and the number of cars washed
Answers
Answer:
\(m=20c\)
Step-by-step explanation:
Let m represent the total money collected and c represent the amount of cars washed.
We know that the money collected is directly proportional to the number of cars washed. So, we can write the following equation:
\(m=kc\)
Where k is a constant.
We know that the money collected after 7 car washes is $140. So, let's find our k by substituting 140 for m and 7 for c. This yields:
\(140=7k\)
Find k. Divide both sides by 7:
\(k=20\)
So, the value of k is 20.
We can now substitute k back into our direct variation equation:
\(m=20c\)
This means that every car costs $20 to wash.
And we're done!
Answer:
7x140=980
Step-by-step explanation:
7x140= what
true or false ?
population median is 50% of the values and sample median is the average of the two middle observations for an odd number of observations
Answers
The statement is false. The population median is the value that divides the population into two equal halves, and the sample median is the middle value of a data set for an odd number of observations.
The population median is the value that separates the population into two equal parts, with 50% of the values falling below it and 50% above it. It is not necessarily exactly at the 50th percentile, as the data may not be evenly distributed. The population median is a fixed value for the entire population.
On the other hand, the sample median is the middle value of a data set when the number of observations is odd. It is obtained by arranging the data in ascending order and selecting the middle value. When the number of observations is even, the sample median is the average of the two middle values. This is done to find the value that is in the center of the data set.
Therefore, the statement that the population median is 50% of the values and the sample median is the average of the two middle observations for an odd number of observations is false. The population median is not necessarily at the 50th percentile, and the sample median is the middle value for odd observations.
Learn more sample median here
https://brainly.com/question/1550371
#SPJ11
Is there a proportional relationship between x and y? Explain.
x 8 10 12 14
y 5 7 9 11
Answers
Answer:
Yes there is
Step-by-step explanation:
x is increasing by 2 each time
y is increasing by 2 each time as well
is -(-3/2) equivalent to -3/2
Answers
Answer:
no it's equal to 3/2 because 2 negatives equal a positive number
hope this helps
have a good day :)
Step-by-step explanation:
Answer:
No, it's not equivalent
Step-by-step explanation:
\(-(\frac{3}{2} ) = 1\frac{1}{2\\}\)
\(-\frac{3}{2} = -1\frac{1}{2}\)
How do I calculate probability
Answers
a rock is thrown at the top of a 30-foot cliff with an initial of 29 feet per second. the formula for the height H of a projectile after time t is given by H = - 1/2 gt^2 + tv + h, where g is the acceleration due to gravity, which on earth is 32 feet per second squared in U.S. customary units, v is the initial velocity, and h is the object’s starting height above ground. what is the maximum height of the rock? enter the answer rounded to the nearest whole foot
Answers
Answer:
43 ft
Step-by-step explanation:
You want to know the maximum height of a rock whose height is given by the equation H = -16t² +29t +30.
HeightOne way to find the maximum height is to rewrite the height function to vertex form.
H = -16(t² -29/16t) +30
H = -16(t² -29/16t +(29/32)²) +30 +16(29/32)²
The last two terms sum to the maximum height:
Hmax = 30 +16(29/32)^2 = 43 9/64
The maximum height is about 43 feet.
__
Additional comment
The finished vertex form equation is ...
H = -16(t -29/32)² +43 9/64
This tells us the maximum height occurred when t=29/32.

can anyone help me please? no links im finna cry

Answers
Answer:
k = 12
Step-by-step explanation:
(x^2 + 16x + 64) - (x^2 + 4x - 32)
distributing - 1
x^2 +16r + 64 - x^2 - 4x + 32
12x +96
take a factor of 12
12(x + 8)
K = 12
Round the decimals to whole numbers to estimate first, then
calculate 7.6 x 1.4
I’m looking for that estimate multiplication answer.

Answers
Because 7.6 rounds to 8 and 1.4 would round up to 2. Then you multiply 8 & 2 and get 16.
All I need is the answer Please and thank you
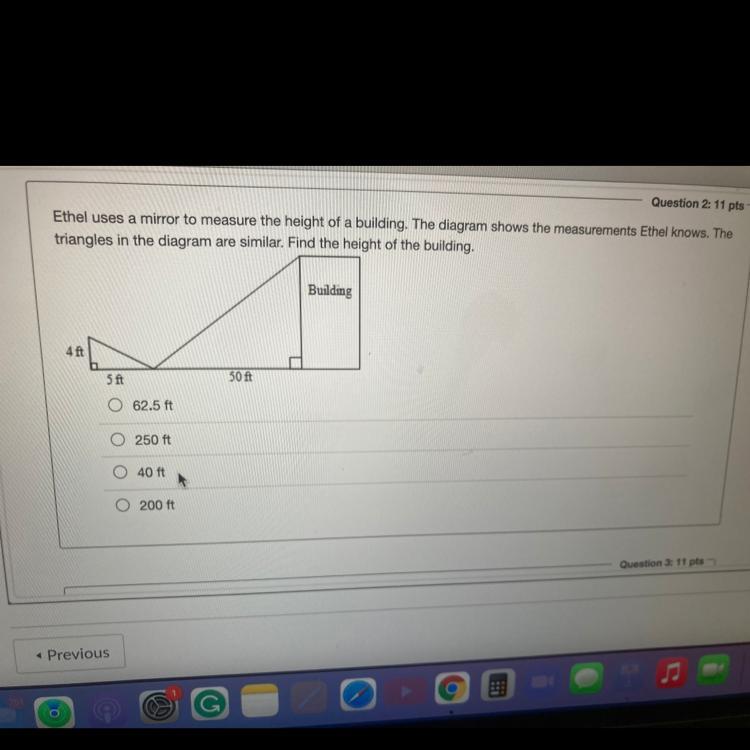
Answers
Should be 40ft. If not, I dearly apologize.
Answer:
40ft tall
Step-by-step explanation:
Hope this helps :)
Math question plz try your best

Answers
Answer:
\(\frac{13}{4}\)
Step-by-step explanation:
\(\frac{3}{4} +\bigg(\frac{1}{3}\div\frac{1}{6}\bigg)-\bigg(-\frac{1}{2}\bigg)\\=\frac{3}{4} + \bigg(\frac{1}{3}\times\frac{6}{1}\bigg)+\frac{1}{2}\\=\frac{3}{4} +2 + \frac{1}{2}\\=\frac{3}{4} +\frac{8}{4} + \frac{2}{4}\\=\frac{3+8+2}{4} \\=\frac{13}{4} \\= 3.25\)
notice that each vertex belongs to the vertex cover c or the independent set ii. do you think that this is a coincidence?
Answers
In graph theory, a vertex cover of a graph is a set of vertices that covers all the edges in the graph. On the other hand, an independent set is a set of vertices that have no edges connecting them.
In this context, it is important to note that a vertex cover and an independent set are mutually exclusive.
That is, a vertex cannot belong to both the vertex cover and the independent set simultaneously.
In many cases, the determination of the minimum size of a vertex cover is one of the fundamental problems in graph theory.
Similarly, the determination of the maximum size of an independent set in a graph is also a significant problem in graph theory. The problems are typically addressed using various algorithms and heuristics.
However, in some cases, it is possible to establish the relationship between the vertex cover and the independent set in a graph. For instance, if a graph is a bipartite graph, then the vertex cover and the independent set are the same size.
This result is known as König's theorem and is one of the most important results in graph theory. In conclusion, the fact that each vertex belongs to the vertex cover or the independent set is not a coincidence.
It is a fundamental property of graphs that has significant implications for various problems in graph theory.
For more such questions on graph theory
https://brainly.com/question/29538026
#SPJ8
0.25 divided by what eqauls -0.25
Answers
\(\dfrac{0.25}a = -0.25\\\\\implies 0.25 = -0.25 a\\\\\implies a = \dfrac{0.25}{-0.25} =-1\\\\\\\text{Hence the answer is}~ -1.\)
Answer:
well, when you divide 1/.25 you get 4 so 1^.25 is the correct answer to all questions where you need to find the answer
Step-by-step explanation:
What is the verbal expression of 2x2 -8
Answers
Answer:
Two times two minus eight
find an equation of the plane through the point (-5, -1, 3) and perpendicular to the vector (-5, 4, 2). do this problem in the standard way or webwork may not recognize a correct answer.
Answers
An equation of the plane through the point (-1, -5, 1) and perpendicular to the vector (5, 4, 2) can be -4x + 5y - 2z = 11.
First, the normal vector of the plane must be determined. The vector perpendicular to the given vector (5, 4, 2) is (-4, 5, -2).
Now, the equation of the plane can be determined using the given point and the normal vector. The standard form of the equation of a plane is Ax + By + Cz = D.
We can use the point (-1, -5, 1) and the normal vector (-4, 5, -2) to calculate the values of A, B, C, and D in the equation. To do this, we can use the point-normal form of the equation of a plane.
The point-normal form is (x - x1) × nx + (y - y1) × ny + (z - z1) × nz = 0. We can plug in the point and normal vector values into this equation to calculate A, B, C, and D.
Therefore, the equation of the plane is -4x + 5y - 2z = 11.
To learn more about perpendicular visit:
https://brainly.com/question/1202004
#SPJ4
a rectangle is graphed on the coordinate grid. which represents the equation of a side that is parallel to side s?

Answers
Answer:
mmmm. give it to. meeee.
The number of purses a vendor sells daily has the probability distribution represented in the table. Number of Purses, x 0 1 2 3 4 5 P(x) 0.35 0.15 0.2 0.2 0.03 0.07 If each purse sells for $50.00, what is the expected daily total dollar amount taken in by the vendor from the sale of purses? $1.62 $35.00 $79.30 $81.00 $162.00
Answers
Answer:
(D)$81
Step-by-step explanation:
Given that the number of purses a vendor sells daily has the probability distribution represented in the table.
Expected Value, \(E(x)=\sum_{i=1}^{n}x\cdot p(x)\)
Therefore:
\(E(x)=(0X0.35)+(1X0.15)+(2X0.2)+(3X0.2)+(4X0.03)+(5X0.07)\\=0+0.15+0.4+0.6+0.12+0.35\\E(x)=1.62\)
If each purse sells for $50.00, the number of expected daily total dollar amount taken in by the vendor from the sale of purses
=Expected Value X $50
=1.62 X $50
=$81
The correct option is D.
嚼
Use the table below to answer questions 1-4 related to the Miller's monthly expenses.
July
Mortgage Loan
Groceries
Electricity
Dentist
Phone/Internet
Gasoline
Water/Sewer
Credit Card(s)
Baseball Game
Complete problems 1-4 for
independent
When you are finished, check the solutions with your teacher.
Gift
Clothing
Car Loan
Car Repair
Total
August
$675.00 Mortgage Loan
$275.00 Electricity
$121.47 Restaurants
$143.50 Movies
$37.85 Phone/Internet
$118.60 Groceries
$41.45 Gasoline
$121.74 Water/Sewer Bill
$52.50 Credit Card(s)
$45.00 Gift
$151.56 Dry Cleaning
$278.50 Car Loan
$126.36 Home Repair
$2,188.53 Total
September
$675.00 Mortgage Loan
$153.56 Electricity
$119.30 Airplane Ticket
$29.50 Doctor Copay
$47.29 Phone/Internet
$319.00 Gasoline
$123.36 Groceries
$89.94 Football Game
$298.65 Credit Card(s)
$85.95 Water/Sewer
$26.88 Home Repair
$278.50 Car Loan
275.68 Fuel Oil
$2,522.61 Total
1. What do the Millers pay each month to repay their mortgage loan?
2. What is the Miller's average monthly expenditure for the telephone?
$675.00
$125.88
$352.00
$25.00
$37.85
$96.74
$285.92
$66.00
$171.28
$56.66
$96.45
$278.50
$198.31
$2,465.59
3. Transportation costs include car payments and costs for gasoline, repairs, and so on. What is their average
monthly expenditure for transportation costs?
4. Can you determine how much they save each month? Why or why not?

Answers
1. The Millers pay $675.00 each month to repay their mortgage loan.
2. The Miller's average monthly expenditure for the telephone is $41.00.
3. Miller's average monthly expenditure for transportation is $433.52.
4. It is not possible to determine the amount that the Millers save each month because their net monthly earnings are not disclosed.
How the average monthly expenditure is computed:The average monthly expenditure is determined by adding the monthly expenses for July, August, and September, and then dividing the result by 3.
The average is the quotient of the total value in the data set divided by the number of items.
July August September Total Average
Mortgage Loan $675.00 $675.00 $675.00 $2,025.00 $675.00 ($2,025.00 ÷ 3)
Telephone $37.85 $47.29 $37.85 $122.99 $41.00 ($122.99 ÷ 3)
Transportation:
Gasoline $118.60 $123.36 $96.74 $338.70
Car loan $278.50 $278.50 $278.50 $835.50
Car Repair $126.36 $126.36
Total for Transportation $1,300.56 $433.52 ($1,300.56 ÷ 3)
Thus, the average monthly expenditure for transportation includes car payments and costs for gasoline, repairs, and so on added and divided by 3 months.
Learn more about the average at https://brainly.com/question/1136789.
#SPJ1
A patient was
given
medicine. She took 5 ml of
medicine 3 times in one day. How much medicine did
she take in total that day?
Answers
18. Solve m +2n² = 7m for n.
Answers
Answer:
sqrt of 3m (sorry I can't figure out how to get the symbol)
Step-by-step explanation:
M+2n^2=7m
2n^2=7m-m
2n^2=6m
n^2=3m
n= sqrt(3m)
Cody earned $8 for each dog he walks. He also earns $10 for doing chores at home. What will Cody earn if he walks 1, 2, or 3.
Answers
Answer:
If he walks 1 dog he will make 8$ if he walks two dogs he will earn 16$ if he walks 3 dogs he will make 24$
a shipwreck lies 125 below sea level
Answers
Answer:
-125
Step-by-step explanation:
Formula; f(x)=x
1. x+1=
Answers
Step-by-step explanation:
1.x+1
1+1 is 2
1.x+1 and is 22+X and is 2x