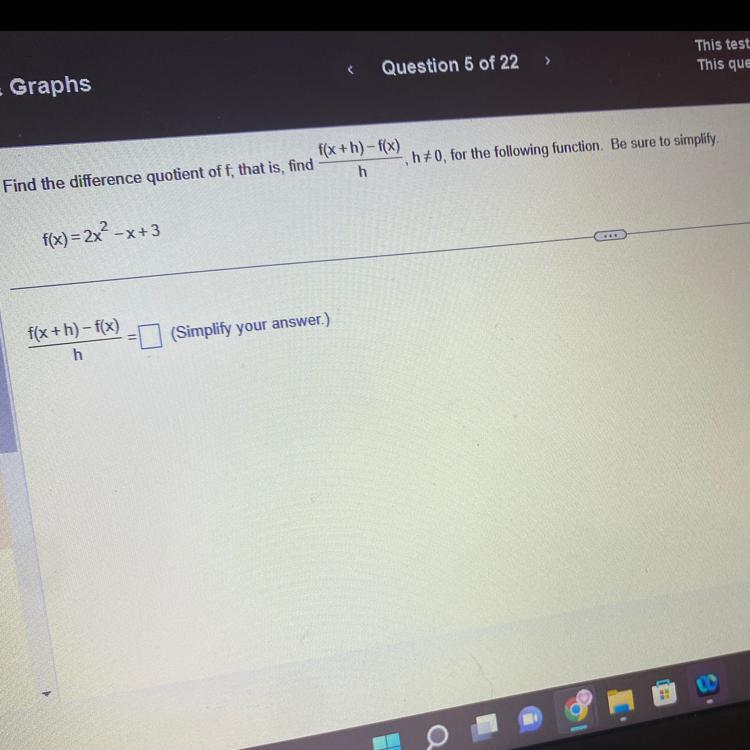
Find the area and circumference of the circle.
(x - 1)^2 + (y-2)^2 = 100
The area of the circle is ______
(Simplify your answer. Type an exact answer, using as needed.)
The circumference of the circle is _____ (Simplify your answer. Type an exact answer, using as needed.)
Answers
The area of the circle is 100π square units, and the circumference of the circle is 20π units.
The equation of the circle is given by (x - 1)² + (y - 2)² = 100. By comparing the equation with the standard form of a circle, we can determine that the center of the circle is located at (1, 2), and the radius is 10 units.
Using these values, we can calculate the area and circumference of the circle.
Area of the circle = πr² = π(10)² = 100π square units.
Circumference of the circle = 2πr = 2π(10) = 20π units.
Therefore, the area of the circle is 100π square units, and the circumference of the circle is 20π units.
Learn more about radius here:
brainly.com/question/32954211
#SPJ11
Related Questions
19x=y
in standerds form
Answers
Answer:
19x − y = 0
__
how to simplify y = 34 - 0.5x
Answers
Answer:
y = 0.5
Step-by-step explanation:
identify the surface whose equation is given. rho2(sin2(φ) sin2(θ) + cos2(φ)) = 16
Answers
The equation provided is: ρ²(sin²(φ)sin²(θ) + cos²(φ)) = 16, This equation is in spherical coordinates,
where ρ represents the radial distance from the origin, φ is the polar angle (or the angle between the positive z-axis and the vector), and θ is the azimuthal angle (or the angle between the positive x-axis and the projection of the vector onto the xy-plane).
Now, let's analyze the equation further: 1. Divide both sides of the equation by 16 to isolate ρ²: ρ² = 16 / (sin²(φ)sin²(θ) + cos²(φ)) 2. Take the square root of both sides to find ρ: ρ = √(16 / (sin²(φ)sin²(θ) + cos²(φ))).
From this, we can see that the surface is defined by the radial distance ρ, which depends on the angles φ and θ. This indicates that the given equation represents a 3-dimensional surface in spherical coordinates.
To know more about equation click here
brainly.com/question/649785
#SPJ11
Answer fast!!!!!!!!!!!!!!

Answers
You need to compute the 99% confidence interval for the population mean. How large a sample should you draw to ensure that the sample mean does not deviate from the population mean by more than 1.3
Answers
To compute the 99% confidence interval for the population mean, you need to determine the appropriate sample size to ensure that the sample mean does not deviate from the population mean by more than 1.3. The key terms involved in this process are the confidence interval, sample size, population mean, and sample mean.
The confidence interval represents the range within which the population parameter (in this case, the population mean) is likely to fall, given a certain level of confidence. A 99% confidence interval means that you are 99% confident that the true population mean falls within the specified range.
To calculate the required sample size, you will need to use the formula for the margin of error (E), which is E = (Zα/2 * σ) / √n, where Zα/2 is the critical value associated with the desired level of confidence (99%), σ is the population standard deviation, and n is the sample size.
Since you want the sample mean to not deviate from the population mean by more than 1.3, you will need to set E = 1.3 and solve for n. After finding the critical value for a 99% confidence interval (which is approximately 2.576) and assuming you know the population standard deviation, you can plug these values into the formula and solve for n.
By doing this, you will be able to determine the appropriate sample size to ensure that the 99% confidence interval for the population mean is within 1.3 units of the sample mean.
To learn more about confidence interval click here
brainly.com/question/22851322
#SPJ11
Solve the problems.
Which correctly explains the number of solutions of the following system of linear
equations?
y = 6x + 2
y = 6x-2
A The graphs of the equations are parallel lines because they have the same slope
but different y-intercepts. The system has no solution.
B
The graphs of the equations are lines that intersect at one point because the
equations have the same slope but different y-intercepts. The system has
exactly one solution.
C The graphs of the equations are lines that intersect at one point because the
equations have the same slope and same y-intercept. The system has exactly
one solution,
D The graphs of the equations are the same line because the equations have the
same slope and same'y-intercept. The system has infinitely many solutions
2 Draw a line from each system of linear equations to the comma
solution to the
Answers
Answer: where is the picture
Step-by-step explanation:
Answer:
A because they create parallel lines but only have different intercepts.
Please help I have a learning disablity and need help.
What is the coefficient in the expression?
10 – 6 + 5n
5
6
10
5n
-6
Answers
divide 240 g in the ratio 5:3:4
Answers
im not good at this stuff
please help <3
:)

Answers
Answer:
1. 3.33
2. 8.75
3. 4.8
4. 2.5
Step-by-step explanation:
The first three terms of an arithmetic sequence are as follows.
3, -2, -7
Find the next two terms of this sequence.
Answers
Answer:
The sequence is -5 so the next 2 values are -12, and -17
Step-by-step explanation:
plzz answer this question i will mark brainliest

Answers
Answer:
Step-by-step explanation:
line 1.
y=3
line 2.
x=-1.2
line 3.
x=3
line 4.
y=-2.6
length=3-(-1.2)=3+1.2=4.2
width=3-(-3)=3+3=6
area=4.2×6=25.2
Change the word phrase to an algebraic expression. Use x to represent the number. The product of 9 and two more than a number
Answers
The algebraic expression for "The product of 9 and two more than a number" is 9(x + 2).
In the given word phrase, "a number" is represented by the variable x. The phrase "two more than a number" can be translated as x + 2 since we add 2 to the number x. The phrase "the product of 9 and two more than a number" indicates that we need to multiply 9 by the value obtained from x + 2. Therefore, the algebraic expression for this word phrase is 9(x + 2).
"A number": This is represented by the variable x, which can take any value.
"Two more than a number": This means adding 2 to the number represented by x. So, we have x + 2.
"The product of 9 and two more than a number": This indicates that we need to multiply 9 by the value obtained from step 2, which is x + 2. Therefore, the algebraic expression becomes 9(x + 2).
In summary, the phrase "The product of 9 and two more than a number" can be algebraically expressed as 9(x + 2), where x represents the number.
Learn more about algebraic expression:
https://brainly.com/question/4344214
#SPJ11
what are the answers to 13, 14, 16, and 17? pls help it will mean a lot :)

Answers
14. 11/25
16. 8/9
I don’t know what is an answer of 17 sorry...:(
If the original quantity is 8 and the new quantity
is 2, what is the percent decrease?
Answers
If the original quantity is 8 and the new quantity is 2, then the correct answer is 75%.
How did we figure this out?
For this question we need to subtract and multiply the numbers. We know that 2 = 25% of 8 so:
\(\boxed{8-2=6}\\\boxed{6/2=3}\)
We are going to take that 25% and multiply it with 3 to get are final answer.
What is the missing number of 25 and 3?\(\boxed{25*3=75}\\\boxed{So,2=75}\)
Therefore, If the original quantity is 8 and the new quantity is 2, then the correct answer is 75%.
In the figure, ZQ is congruent to ZT and ZR is congruent to ZU. What are the measures of ZP and ZS?

Answers
Answer:
Angle P: 110°
Angle S: 110°
Step-by-step explanation:
Since angle P and angle S are congruent, that means they are equal to each other.
Setup an equation so that they are equal to each other and solve for x.
2x + 10 = 3x - 40
2x - 2x +10 = 3x -2x - 40
10 = x - 40
10 + 40 = x - 40 + 40
x = 50
For each angle, plugin for x and solve. You should get the same answer since they are congruent.
Angle P:
2x + 10
2(50) + 10
100 + 10
110°
Angle S:
3x - 40
3(50) - 40
150 - 40
110°
Explain why the descriptions "right 5 up 2", "right 10 up 4", "left 5 down 2", "right 5/2 up 1", and "left 1 down 2/5" all describe the same inclination for a straight line.
Answers
All of the translations describes the same inclination for a straight line because the they all have a pitch (slope) of 2/5.
How to determine the pitch (slope) of a straight line?Mathematically, the pitch (slope) of a geometric figure or straight line can be calculated by using this formula:
Pitch (slope) = V/H
Where:
V represents the rising vertical distance of an object.H represents the horizontal distance an object runs through.Based on the information provided, the pitch (slope) of this line is given by:
Pitch (slope) = Up 2/Right 5 = 2/5
Pitch (slope) = Up 4/Right 10 = 2/5
Pitch (slope) = Down 42/Left 5 = 2/5
Pitch (slope) = Up 1/Right 5/2 = 2/5
Pitch (slope) = Down 2/5/Left 1 = 2/5
Read more on pitch here: brainly.com/question/6781555
#SPJ1
What is antiderivative of sin?
Answers
The antiderivative of sin is -cos(x) + C.
The antiderivative of a function is the inverse operation of differentiation which is is also known as its indefinite integral.
So, the integral of sin
∫sin(x) = -cos(x) + C
where C = constant of integration.
This can be verified by differentiating -cos(x) + C with respect to x, which gives sin(x).
Learn more about indefinite integral from the below link:
https://brainly.com/question/28036871
#SPJ4
can you help me with this math

Answers
Answer:
B. (1, -2)
Step-by-step explanation:
In order to for it to be a function, the inputs need to have only one output.
The table shows:
(-1, 2), (0, -4), (1, -2), (1, 5), (2, 0), (3, 2), (4, 9)
If a x-value is repeating it is not a function.
a cylinder has a right cone removed from it as shown. both the cylinder and cone have a radius of 5 cm, a height of 5 cm, and their bases exactly correspond. find the area of a cross section of the shape that is formed by the intersection of the solid and a plane parallel and 2 inches above the base.
Answers
The area of a cross section of the shape formed by the intersection of the solid and a plane parallel and 2 inches above the base is 20.93 cm².
Calculate the area of the cylinder.
A cylinder's surface area is determined by multiplying its base circumference by its height.
2r, where r is the cylinder's radius (5 cm), equals the circumference of the cylinder.
Therefore, the area of the cylinder is 2πr x 5 cm = 2π x 5 cm2 = 31.4 cm².
Calculate the area of the cone.
A cone's area is determined by multiplying its height by a factor of three times the base's radius.
2r, where r is the cone's radius (5 cm), equals the circumference of the cone.
Therefore, the area of the cone is 1/3 x 2πr x 5 cm = 2π x 5 cm2 / 3 = 10.47 cm².
Determine the cross section area.
The area of the cylinder less the area of the cone equals the area of the cross section.
Therefore, the area of the cross section is 31.4 cm2 - 10.47 cm2 = 20.93 cm².
To know more about cross section visit:
https://brainly.com/question/23509625
#SPJ4
HELP WILL MARK BRAINLIEST PLSS
John walks in the bearing of 75° and stops when he is 12 km North of his starting point.
How far did John walk?

Answers
Answer:
It number 1 trust me pls se
Step-by-step explanation:
The mean percent of childhood asthma prevalence in 43 cities is %. A random sample of of these cities is selected. What is the probability that the mean childhood asthma prevalence for the sample is greater than %? interpret this probability. Assume that %.
Answers
In 13.567% of the 30 cities, the mean prevalence of childhood asthma will be higher than 2.5%.
Given that:
X: childhood asthma prevalence
With mean u = 2.22%
and standard deviation σ= 1.39%
To find : Determine the probability that the average prevalence of childhood asthma in a sample of n cities is higher than 2.5%.
Although we are unsure about the distribution of the variable, keep in mind that from n ≥ 30, the sampling distribution can be roughly compared to the normal distribution according to the central limit theorem:
X≈N(μ;σ²/n)
Additionally, compute the requested probability using the standard normal distribution:
P(X>2.5)= 1 - P(X≤2.5)
Determine the Z value given the X value:
Z = (X - u)/ (σ/√n)
Z = (2.5-2.2)/(1.39/√30)
Z = 1.10
Using the Z-tables you have to look for the value of
P(Z≤1.10)= 0.86433
1 - 0.86433= 0.13567
Then P(X>2.5)= 1 - P(X≤2.5)= 1 - P(Z≤1.10)= 1 - 0.86433= 0.13567
So, 13.567% of the 30 cities will have a mean childhood asthma prevalence greater than 2.5%
To learn more about probability click here:
brainly.com/question/11234923
#SPJ4
Consider the following 8 numbers, where one labelled ï is unknown.
14, 28, 28, x, 36, 6, 4, 50
Given that the range of the numbers is 59, work out 2 values of x.
Answers
Answer:
177x
Step-by-step explanation:
which of the relations given by the following sets of ordered pairs is a function?
a. {(5,2),(4,2),(3,2),(2,2),(1,2)}{(5,2),(4,2),(3,2),(2,2),(1,2)}
b. {(−4,−2),(−1,−1),(3,2),(3,5),(7,10)}{(−4,−2),(−1,−1),(3,2),(3,5),(7,10)}
c. {(−8,−3),(−6,−5),(−4,−2),(−2,−7),(−1,−4)}{(−8,−3),(−6,−5),(−4,−2),(−2,−7),(−1,−4)}
d. {(−6,4),(−3,−1),(0,5),(1,−1),(2,3)}
Answers
{(5, 2), (4, 2), (3, 2), (2, 2), (1, 2)}, {(−8, −3), (−6, −5), (−4, −2), (−2, −7), (−1, −4)} and {(−6, 4), (−3, −1), (0, 5), (1, −1), (2, 3)} are the sets of ordered pairs considered as a function.
{(−4, −2), (−1, −1), (3, 2), (3, 5), (7, 10)} is not a function.
In mathematics, ordered pair is a pair of numbers that are written in a specific order. They are generally written in (x, y) form. For example (3, 5) is an ordered pair.
The function can also be represented by a set of ordered pairs. A function Is a set of ordered pairs in which no two different ordered pairs have the same value of x coordinate.
Option (a) : {(5, 2),(4, 2),(3, 2),(2, 2),(1, 2)}
No two ordered pairs have the same value of the x coordinate.
So it is a function.
Option (b) : {(-4, -2),(-1, -1),(3, 2),(3, 5),(7, 10)}
Two ordered pairs have the same value of x coordinate (3, 2) and (3, 5).
So, it can not be considered a function.
Option (c) : {(-8, -3),(-6, -5),(-4, -2),(-2, -7),(-1, -4)}
No two ordered pairs have the same value of the x coordinate.
So it is a function.
Option (d) : {(-6, 4),(-3, -1),(0, 5),(1, -1),(2, 3)}
No two ordered pairs have the same value of the x coordinate.
So it is a function.
Therefore, Options (a), (c), and (d) are the functions.
Option (b) is not a function.
For more questions on ordered pairs as function
https://brainly.com/question/11267211
#SPJ4
What percent of 2 is 2/5? Make sure your answer is fully reduced
Answers
Answer:
20%
Step-by-step explanation:
You can get this answer algebraically by following these steps:
2 ÷ 100 ( x ÷ 100 ) = 2/5
2 x/100 = 2/5
2x = 200/5
2x = 40
40 ÷ 2 = 20
∴ x= 20%
Answer:
20%
Step-by-step explanation:
What is a percentage?A percentage is a ratio, or a number expressed in the form of a fraction of 100. Percentages are often used to express a part of a total.
To solve this, we can use this equation:
2 × 0.2 = 0.4 or 2/5Why do we multiply by 0.2?Well, if percentages are fractions of 100, we can convert 20% into \(\frac{20}{100}\), or 0.2.
Therefore, 2/5 is 20% of 2.
What is the measure of angle L?
Round only your final answer to the nearest hundredth.

Answers
Answer:
1.27 radians
Step-by-step explanation:
(04.05, 05.04, 07.04 HC) dy = 5(2x + 3)sin (x2 + 3x +"). x dx Consider the differential equation Part A: Find the equation of the line tangent to the solution curve at the point (0,5). (5 points) Part B: Find the second derivative at (0,5) and use it to determine the concavity of the solution curve at that point. Explain. (10 points) Part C: Find the particular solution y = f(x) with initial condition f(0) = 5. (15 points)
Answers
Part a: The equation of the tangent line is: y - 5 = -15(x - 0)
Part b:The second derivative is a constant value, -15. Since the second derivative is negative, it means the function is concave down at (0, 5).
Part c:The particular solution is y = -10cos(x² + 3x + π) + 15(x² + 3x + π) - 5 - 15π
Part A: To find the equation of the line tangent to the solution curve at the point (0, 5), to follow these steps:
Step 1: Find the derivative of the given differential equation.
Given differential equation: dy/dx = 5(2x + 3)sin(x² + 3x + π)
Differentiate both sides with respect to x:
dy/dx = d/dx (5(2x + 3)sin(x²+ 3x + π))
dy/dx = 5 × (2(sin(x² + 3x + π)) + (2x + 3)cos(x² + 3x + π))
Step 2: Evaluate the derivative at the point (0, 5).
To find the slope of the tangent line at (0, 5), substitute x = 0 into the derivative:
dy/dx = 5 × (2(sin(π)) + (2×0 + 3)cos(π))
dy/dx = 5 × (2(0) + 3(-1)) = -15
Step 3: Use the point-slope form of the equation to write the equation of the tangent line.
The point-slope form of the equation is: y - y1 = m(x - x1), where m is the slope and (x1, y1) is the point (0, 5).
Simplifying, we get: y = -15x + 5
Part B: To find the second derivative at (0, 5) and determine the concavity of the solution curve at that point, follow these steps:
Step 1: Find the second derivative of the given differential equation.
Given differential equation: dy/dx = 5(2x + 3)sin(x² + 3x + π)
Differentiate the previous result for dy/dx with respect to x to get the second derivative:
d²y/dx² = d/dx (-15x + 5)
d²y/dx² = -15
Step 2: Determine the concavity.
Part C: To find the particular solution y = f(x) with the initial condition f(0) = 5, to integrate the given differential equation:
dy/dx = 5(2x + 3)sin(x² + 3x + π)
Step 1: Integrate the equation with respect to x:
∫dy = ∫5(2x + 3)sin(x² + 3x + π) dx
y = ∫(10x + 15)sin(x² + 3x + π) dx
Step 2: Use u-substitution:
Let u = x² + 3x + π, then du = (2x + 3) dx
Now the integral becomes:
y = ∫(10x + 15)sin(u) du
Step 3: Integrate with respect to u:
y = -10cos(u) + 15u + C
Step 4: Substitute back for u:
y = -10cos(x² + 3x + π) + 15(x² + 3x + π) + C
Step 5: Apply the initial condition f(0) = 5:
Substitute x = 0 and y = 5 into the equation:
5 = -10cos(π) + 15(0² + 3(0) + π) + C
5 = 10 + 15π + C
Simplifying,
C = 5 - 10 - 15π
C = -5 - 15π
To know more about equation here
https://brainly.com/question/29657983
#SPJ4
if a fair die is rolled 5 times, what is the probability, rounded to the nearest thousandth, of getting at least 2 fours?
Answers
So the probability, rounded to the nearest thousandth, of getting at least 2 fours in 5 rolls of a fair die is 0.194.
What is the simple definition of probability?A probability is a number that expresses the possibility or likelihood that a specific event will take place. Probabilities can be stated as proportions with a range of 0 to 1, or as percentages with a range of 0% to 100%.
According to the given information:The probability of getting at least 2 fours is the sum of the probabilities of getting exactly 2, 3, 4, or 5 fours:
P(X ≥ 2) = P(X=2) + P(X=3) + P(X=4) + P(X=5)
Using the binomial formula, we can calculate each of these probabilities:
P(X=k) = (n choose k) p^k (1-p)^(n-k)
where (n choose k) is the binomial coefficient, which represents the number of ways to choose k items from n distinct items.
P(X=2) = (5 choose 2) (1/6)² (5/6)³ = 0.1608
P(X=3) = (5 choose 3) (1/6)³ (5/6)² = 0.0322
P(X=4) = (5 choose 4) (1/6)⁴ (5/6)¹ = 0.0013
P(X=5) = (5 choose 5) (1/6)⁵ (5/6)⁰ = 0.00003
Therefore,
P(X ≥ 2) = 0.1608 + 0.0322 + 0.0013 + 0.00003 = 0.1943
So the probability, rounded to the nearest thousandth, of getting at least 2 fours in 5 rolls of a fair die is 0.194.
To know more about probability visit:
https://brainly.com/question/12431044
#SPJ1
SOMEONE PLEASE ANSWER THIS FOR ME CORRECTLY I WILL MAKE YOU THE BRAINLIEST AND GIVE YOU A GOOD RATE UST PLEASE HELP ASAPPPPPPPP!!!!!!!!!!!!!
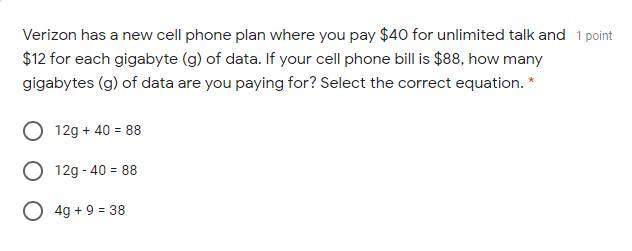
Answers
Answer:
12g+40=88
Step-by-step explanation:
40 represent the unlimited part and the 12g is the 12 dollars per gig.
hope this helped
anyone solve this??????????????????????????????????

Answers
Answer:
16
Step-by-step explanation:
9-9:9 +9 - 9 :9 =
9 - 1 +9 - 1 =
8 +9 - 1 =
17 - 1 =
16
PLWASE HELP I WILL GIVE BRAINLIEST