Determine the two equations necessary to graph the hyperbola with a graphing calculator, y2-25x2 = 25 OA. y=5+ Vx? and y= 5-VR? ОВ. y y=5\x2 + 1 and y= -5/X2+1 OC. and -y=-5-? D. y = 5x + 5 and y= -
Answers
To graph hyperbola equation given,correct equations to use a graphing calculator are y = 5 + sqrt((25x^2 + 25)/25),y = 5- sqrt((25x^2 + 25)/25). These equations represent upper and lower branches hyperbola.
The equation y^2 - 25x^2 = 25 represents a hyperbola centered at the origin with vertical transverse axis. To graph this hyperbola using a graphing calculator, we need to isolate y in terms of x to obtain two separate equations for the upper and lower branches.
Starting with the given equation:
y^2 - 25x^2 = 25
We can rearrange the equation to isolate y:
y^2 = 25x^2 + 25
Taking the square root of both sides:
y = ± sqrt(25x^2 + 25)
Simplifying the square root:
y = ± sqrt((25x^2 + 25)/25)
The positive square root represents the upper branch of the hyperbola, and the negative square root represents the lower branch. Therefore, the two equations needed to graph the hyperbola are:
y = 5 + sqrt((25x^2 + 25)/25) and y = 5 - sqrt((25x^2 + 25)/25).
Using these equations with a graphing calculator will allow you to plot the hyperbola accurately.
To learn more about hyperbola click here : brainly.com/question/32019699
#SPJ11
Related Questions
What is the quotient: (3x2 + 8x – 3) ÷ (x + 3) ?. Answer.
A) 3x2 – 11
B) 3x – 11
C) 3x2 – 11 –
D) 3x – 11 –
Answers
Which algebraic expression represents this word description?
The product of nine and the difference between a number and five
OA. 9x-5
OB. 9(x - 5)
OC. 5-9x
OD. 9(5-x)
Answers
Let the number be represented by x.
The difference between a number and five is (x - 5).
The product of nine and (x - 5) is 9(x - 5).
Therefore, the correct algebraic expression that represents the given word description is option (OB) 9(x - 5).
Prove each of the following statements using strong induction. a. Prove that any amount of postage worth 8 cents or more can be made from 3-cent or 5-cent stamps. b. Prove that any amount of postage worth 24 cents or more can be made from 7-cent or 5-cent stamps. c. Prove that any amount of postage worth 12 cents or more can be made from 3-cent or 7-cent stamps.
Answers
a) By strong induction, any amount of postage worth 8 cents or more can be made from 3-cent or 5-cent stamps.
b) By strong induction, any amount of postage worth 24 cents or more can be made from 7-cent or 5-cent stamps.
c) By strong induction, any amount of postage worth 12 cents or more can be made from 3-cent or 7-cent stamps.
a. Prove that any amount of postage worth 8 cents or more can be made from 3-cent or 5-cent stamps.
Base case: For postage worth 8 cents, we can use two 4-cent stamps, which can be made using a combination of one 3-cent stamp and one 5-cent stamp.
Induction hypothesis: Assume that any amount of postage worth k cents or less, where k is greater than or equal to 8, can be made from 3-cent or 5-cent stamps.
Induction step: Consider any amount of postage worth (k+1) cents. Since k is greater than or equal to 8, we can use the induction hypothesis to make k cents using 3-cent or 5-cent stamps. Then, we can add one more stamp to make (k+1) cents. If the last stamp we added was a 3-cent stamp, we can replace it with a 5-cent stamp to get the same value. If the last stamp we added was a 5-cent stamp, we can replace it with two 3-cent stamps to get the same value. Therefore, any amount of postage worth (k+1) cents can be made from 3-cent or 5-cent stamps.
b. Prove that any amount of postage worth 24 cents or more can be made from 7-cent or 5-cent stamps.
Base case: For postage worth 24 cents, we can use three 8-cent stamps, which can be made using a combination of one 7-cent stamp and one 5-cent stamp.
Induction hypothesis: Assume that any amount of postage worth k cents or less, where k is greater than or equal to 24, can be made from 7-cent or 5-cent stamps.
Induction step: Consider any amount of postage worth (k+1) cents. Since k is greater than or equal to 24, we can use the induction hypothesis to make k cents using 7-cent or 5-cent stamps. Then, we can add one more stamp to make (k+1) cents. If the last stamp we added was a 5-cent stamp, we can replace it with two 7-cent stamps to get the same value. If the last stamp we added was a 7-cent stamp, we can replace it with three 5-cent stamps to get the same value. Therefore, any amount of postage worth (k+1) cents can be made from 7-cent or 5-cent stamps.
c. Prove that any amount of postage worth 12 cents or more can be made from 3-cent or 7-cent stamps.
Base case: For postage worth 12 cents, we can use one 3-cent stamp and three 3-cent stamps, which can be made using a combination of two 7-cent stamps.
Induction hypothesis: Assume that any amount of postage worth k cents or less, where k is greater than or equal to 12, can be made from 3-cent or 7-cent stamps.
Induction step: Consider any amount of postage worth (k+1) cents. Since k is greater than or equal to 12, we can use the induction hypothesis to make k cents using 3-cent or 7-cent stamps. Then, we can add one more stamp to make (k+1) cents. If the last stamp we added was a 3-cent stamp, we can replace it with two 7-cent stamps to get the same value. If the last stamp we added was a 7-cent stamp, we can replace it with one 3-cent stamp and two 7-cent stamps to get the same value. Therefore, any amount of postage worth (k+1) cents can be made from 3
Learn more about strong induction
brainly.com/question/30692296
#SPJ4
The density of glycerin is 20 g/cm3 at 20 0c. find the density of glycerin at 60 0c. the volume coefficient of glycerin is 5.1 x 10-4 0c-1.
Answers
The density of glycerin at 60°C is approximately 19.9592 g/cm³.
To find the density of glycerin at 60°C, we can use the volume expansion coefficient and the given density at 20°C.
The formula for volume expansion is:
ΔV = β * V₀ * ΔT
where:
ΔV is the change in volume,
β is the volume expansion coefficient,
V₀ is the initial volume, and
ΔT is the change in temperature.
In this case, we want to find the change in density, so we can rewrite the formula as:
Δρ = -β * ρ₀ * ΔT
where:
Δρ is the change in density,
β is the volume expansion coefficient,
ρ₀ is the initial density, and
ΔT is the change in temperature.
Given:
ρ₀ = 20 g/cm³ (density at 20°C)
β = 5.1 x 10⁻⁴ °C⁻¹ (volume expansion coefficient)
ΔT = 60°C - 20°C = 40°C (change in temperature)
Substituting the values into the formula, we have:
Δρ = - (5.1 x 10⁻⁴ °C⁻¹) * (20 g/cm³) * (40°C)
Calculating the expression:
Δρ = - (5.1 x 10⁻⁴) * (20) * (40) g/cm³
≈ - 0.0408 g/cm³
To find the density at 60°C, we add the change in density to the initial density:
ρ = ρ₀ + Δρ
= 20 g/cm³ + (-0.0408 g/cm³)
≈ 19.9592 g/cm³
Therefore, the density of glycerin at 60°C is approximately 19.9592 g/cm³.
To know more about volume expansion visit:
https://brainly.com/question/33519730
#SPJ11
Determine whether each pair of expressions is equivalent. Explain your reasoning.

Answers
The answer is:
\(\large\textbf{They aren't equivalent.}}\)
In-depth explanation:
To determine the answer to this problem, we will use one of the exponent properties:
\(\sf{x^{-m}=\dfrac{1}{x^m}}\)
And
\(\sf{\dfrac{1}{x^{-m}}=x^m}\)
Now we apply this to the problem.
What is 4⁻³ equal to? Well according to the property, it's equal to:
\(\sf{4^{-3}=\dfrac{1}{4^3}}\)
And this question asks us if 4⁻³ is the same as 1/4⁻3.
Well according to the calculations performed above, they're not equivalent.
Which is 1/3 + 1/4?
Plz help

Answers
Answer:
B!
Step-by-step explanation:
you have to simply the 2/6 to 1/3
Answer:
7/12
Step-by-step explanation
Write all numerators above the LCD (least common denominator) 12
what does it have? (-2,1)?

Answers
Answer: B,C,D
21
Step-by-step explanation:
(21-21)+(21-21)+21 = 0+0+21 = 21
A system of linear equations is shown below, where A and B are real numbers.
3x + 4y = A
Bx – 6y = 15
What values could A and B be for this system to have no solutions?
Answers
Answer:
A = 0; B = -9/2
Step-by-step explanation:
To have no solutions, you need parallel lines with equal slopes and different y-intercepts.
3x + 4y = A Eq. 1
Bx - 6y = 15 Eq. 2
In Eq. 1, notice that the coefficient of x is 3/4 of the coefficient of y.
We must have the same ratio for the coefficients in Eq. 2.
B/(-6) = 3/4
4B = -6(3)
4B = -18
B = -9/2
Now we have
3x + 4y = A Eq. 1
-9/2 x - 6y = 15 Eq. 2
How do we change the left side of the second equation into the left side of the first equation? -6/4 = -3/2 and also -9/2 ÷ 3 = -3/2
To change the left side of the second equation into the left side of the first equation, divide the left side by -3/2.
If we divide 15 by -3/2 we get -10.
The equation -9/2 x - 6y = -10 is the same as Eq. 1, so that would create a system of equations with only one equation and an infinite number of answers.
To have no equations, the y-intercepts must be different, so A can be any number other that -10.
Answer: A = 0; B = -9/2
Select ALL the options that describe the best measure of center to represent the data in the dot plot
- Mode
- Mean
- Range
- Median
- Interquartile Range
Answers
Answer:
Hi! Based on your question, you would like to know the best measure of center to represent the data in a dot plot. Here are the options to consider:
1. Mode
2. Mean
3. Range
4. Median
5. Interquartile Range
However, without an actual dot plot to analyze, I am unable to provide specific advice on which measure(s) of center would be best for representing the data. If you can provide a dot plot or specific data points, I will gladly help you determine the best measure(s) of center for your data.
To know more about dot plot refer here:
https://brainly.com/question/22746300#
#SPJ11
The options that describe the best measure of center to represent the data in the dot plot are Mode and Median.
Based on the information provided, the best measure of center to represent the data in the dot plot would be:
Mode: The mode represents the value(s) that appear most frequently in the data and can be a good measure of center when there are clear peaks or modes in the distribution.
Median: The median represents the middle value in a dataset when it is arranged in ascending or descending order. It is a robust measure of center that is not affected by extreme values or outliers.
Both the mode and median are suitable measures of center for representing the data in a dot plot. However, the dot plot alone does not provide information about the mean, range, or interquartile range.
Know more about Median here:
https://brainly.com/question/16408033
#SPJ11
What equation in slope intercept form represents the line that passes through the two point? (6.9,5.9), (10.9,-2.1)
Answers
Answer:
y = 2x + b
I dont know what b is but the slope is 2 I think
solve this algebraic expression
\(16a {}^{4} - 4a {}^{2} - 4a - 1\)
![solve this algebraic expression [tex]16a {}^{4} - 4a {}^{2} - 4a - 1[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/rTNTFBv1mFwXSTiMKF2CooIqSISBg7wV.jpeg)
Answers
SOLVING STEPS
Tat-42-40-1
= baT.
(40'740#1)
=16a4 - pati)? = (a'+ zaHi) (42°- 20-1) a'+ sabtb"= atbs
a-B'= (ath) (0-1)
![solve this algebraic expression [tex]16a {}^{4} - 4a {}^{2} - 4a - 1[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/AO967Oo3RnOjKxDLTI966LlwKwrEXwt1.png)
Answer:
The factored form is,
\((4a^2+2a+1)(4a^2-2a-1)\)
Step-by-step explanation:
We have,
\(16a^4-4a^2-4a-1\\factoring,\\We\ can \ write \ 16a^4 \ as \ (4a^2)^2\\Also,\\then we have,\\(4a^2)^2-(4a^2+4a+1)\\Now, 4a^2 + 4a + 1 \ is \ a \ perfect \ square,\\4a^2 + 4a + 1 = (2a)^2 + 2(2a) + 1\\= (2a + 1)^2\\so, we \ have,\\(4a^2)^2 - (2a + 1)^2\\\)
Using the difference of square formula,
\(x^2 - y^2 = (x+y)(x-y)\\with,\\x = 4a^2,\\y = 2a+1,\\we \ get,\\(4a^2+2a+1)(4a^2-2a-1)\)
Which is the factored form,
Select the correct answer.
A tractor-trailer travels 205.296 miles in 3.12 hours. What is the speed at which the tractor-trailer is traveling?
A.
62.05 miles per hour
B.
63.2 miles per hour
C.
64.05 miles per hour
D.
65.8 miles per hour
E.
66.5 miles per hour
Answers
Answer:
D.
Step-by-step explanation:
205.296/3.12 = 65.8
Answer:
:D
Step-by-step explanation:
The sum of the squares of two consecutive even integers is 1684. Find the integers.
Answers
The possible values of two consecutive even integers, of which the sum of their squares is 1684, are 28 and 30 for positive integers, while for negative integers, they are -28 and -30.
The difference between two consecutive even integers is 2.
Let the integers be a and (a+2). Then,
a² + (a + 2)² = 1684
a² + a² + 4a + 4 = 1684
2a² + 4a - 1680 = 0
a² + 2a -840 = 0
Hence, we get a quadratic equation.
There are three methods of solving a quadratic equations: by factoring, completing the square, and by using the abc formula.
Use the factoring method:
a² + 2a -840 = (a - 28) (a + 30)
a = 28 and a = -30
Hence, if the integers are positive, they are: 28 and 30.
If the integers are negative, they are -28 and -30.
Learn more about quadratic equation here:
https://brainly.com/question/30164833
#SPJ4
SOLVE EQUATION (if correct i will give stars)
x^2 = 36/121
Answers
Step-by-step explanation:
x² = 36/121
move terms to left side
x² - 36/121 = 0
1/121 (121x² - 36) = 0
121x² - 36 = 0
Use quadratic formula
x= -b + √b² - 4ac / 2a
a = 121
b= 0
c= 36
x = -0 + √0² - 4.121 (-36) / 2.121
x = + 132/ 242
sperate the equation
x = 131/242
x = -131/242
x = 6/11
x= -6/11
With separation of variables, it is extra essential to use Leibniz notation, since we will need to move dy and dx to different sides of the equation as part of our work.
Answers
it's essential to use Leibniz notation when using separation of variables to solve differential equations.
When using separation of variables to solve a differential equation, we begin by separating the variables, typically denoted as y and x. This involves isolating all y terms on one side of the equation and all x terms on the other side.
At this point, we have an equation of the form f(y)dy = g(x)dx, where f(y) and g(x) are some functions of y and x, respectively. To solve for y, we integrate both sides of the equation with respect to their respective variables. However, it's important to use Leibniz notation (i.e., dy and dx) to keep track of which variable we are integrating with respect to.
Specifically, we write ∫ f(y)dy = ∫ g(x)dx, which means that we integrate f(y) with respect to y and g(x) with respect to x. If we were to use prime notation instead (i.e., y' and x'), it would be unclear which variable we were integrating with respect to, since both y' and x' represent derivatives.
After integrating both sides, we obtain an equation in terms of y and x that we can use to solve for y. This is why it's essential to use Leibniz notation when using separation of variables to solve differential equations.
To learn more about Leibniz notation visit: https://brainly.com/question/14986877
#SPJ11
Look at this graph:
y
x
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
What is the slope?
Simplify your answer and write it as a proper fraction, improper fraction, or integer.
Answers
The slope of the line on this graph is equal to 1/4.
How to calculate the slope of a line?In Mathematics, the slope of any straight line can be determined by using the following mathematical equation;
Slope (m) = (Change in y-axis, Δy)/(Change in x-axis, Δx)
Slope (m) = rise/run
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Substituting the given data points into the slope formula, we have the following;
Slope (m) = (50 - 30)/(90 - 10)
Slope (m) = 20/80
Slope (m) = 1/4.
In this context, we can reasonably infer and logically deduce that the slope of the line on this graph is equal to 0.25 or 1/4.
Read more on slope here: brainly.com/question/3493733
#SPJ1

You spin a spinner that has 12 equal-sized sections numbered 1 to 12. Find the probability of p(less than 5 or greater than 9)
Answers
The probability of getting a number less than 5 or greater than 9 is:
P = 0.583
How to find the probability for the given event?The probability is equal to the quotient between the number of outcomes for the given event and the total number of outcomes.
The numbers that are less than 5 or greater than 9 are:
{1, 2, 3, 4, 10, 11, 12}
So 7 out of the total of 12 outcomes make the event true, then the probability we want to get is the quotient between these numbers:
P = 7/12 = 0.583
LEarn more about probability at:
https://brainly.com/question/25870256
#SPJ1
determine if the two triangles are congruent. if they are, state how you know.
Answers
Answer:
Two shapes are congruent if there length and size or breadth are same
Find the maximum and minimum volumes of a rectangular box whose surface area equals 9000 square cm and whose edge length (sum of lengths of all edges) is 520 cm. Hint: It can be deduced that the box is not a cube, so if x, y, and z are the lengths of the sides
Answers
The maximum volume of the rectangular box is 975,000 cubic cm, and the minimum volume is 405,000 cubic cm.
Let's solve the problem step by step. We are given that the surface area of the rectangular box is 9000 square cm and the sum of the lengths of all edges is 520 cm. We need to find the maximum and minimum volumes of the box.
To find the maximum volume, we need to consider the case where the box is a cube. In a cube, all sides have equal lengths. Let's assume the length of each side is 'a'.
The surface area of a cube is given by 6a^2, and in this case, it is equal to 9000 square cm. So we have:
\(6a^2 = 9000\)
Dividing both sides by 6, we get:
\(a^2 = 1500\)
Taking the square root of both sides, we find:
\(a = \sqrt{1500} \\= 38.73 cm\)
The sum of the lengths of all edges of a cube is given by 12a, so we have:
12a = 12 * 38.73
= 464.76 cm
The maximum volume of the cube-shaped box is:
\(a^3 = 38.73^3\)
= 975,000 cubic cm.
To find the minimum volume, we need to consider the case where the box is not a cube. In this case, let's assume the lengths of the sides are 'x', 'y', and 'z'. We know that the sum of the lengths of all edges is 520 cm, so we have:
4(x + y + z) = 520
Dividing both sides by 4, we get:
x + y + z = 130
We need to maximize the volume of the box, which occurs when the sides are as unequal as possible.
In this case, let's assume x = y and z = 2x. Substituting these values into the equation above, we have:
2x + 2x + 2(2x) = 130
Simplifying, we get:
6x = 130
x = 21.67 cm
Substituting the values of x and z back into the equation, we find:
y = 21.67 cm and z = 43.33 cm
The minimum volume of the rectangular box is:
x * y * z = 21.67 * 21.67 * 43.33
= 405,000 cubic cm.
Learn more about volume here:
https://brainly.com/question/29205460
#SPJ4
awnser please correctly :(

Answers
(100, 600)
1/6 or 100/600 is the slope. You can find the Y intercept where X = 0, so the Y intercept would be 0. The equation would be Y = 1/6 + 0
(01.06 LC)
Expand and simplify: (2x + 5y) (x - 3y) (5 points)
Answers
Answer:
2x² - xy - 15y²
Step-by-step explanation:
(2x + 5y)(x - 3y)
Each term in the second factor is multiplied by each term in the first factor, that is
2x(x - 3y) + 5y(x - 3y) ← distribute parenthesis
= 2x² - 6xy + 5xy - 15y² ← collect like terms
= 2x² - xy - 15y²
sophia got a 95% on her statistics mid-term and a 91% on her calculus mid-term. the grades on both tests were normally distributed. the statistics grades had a mean of 87%, with a standard deviation of 7%, while the calculus grades had a mean of 85% with a standard deviation of 4%. on which test did sophia do better, compared to the rest of her class? how can you tell?
Answers
Sophia did Calculus test better ompared to the rest of her class, as her z-score for Statistics was lower than her z-score for Calculus
We know that the formula for the z-score is: \(z=\frac{x-\mu}{\sigma}\)
where x is the observed value
μ is the mean of the sample
σ is the standard deviation of the sample
Sophia got a 95% on her statistics. The grades had a mean of 87%, with a standard deviation of 7%
So, her z-score for statistics would be:
\(z_s=\frac{95-87}{7}\\\\z_s=1.14\)
She got a 91% on her calculus mid-term. The grades had a mean of 85%, with a standard deviation of 47%
So, her z-score for statistics would be:
\(z_c=\frac{91-85}{4}\\\\z_c=1.5\)
Since her z-score for Statistics was lower than her z-score for Calculus, she did Calculus test better.
Learn more about the z-score here:
https://brainly.com/question/29120012
#SPJ4
(9c + 3) + (-6c + 8)
Answers
Answer:
3c +11 .........................
a teacher wants to create a graph of the students' scores on the final exam and see what the distribution looks like, looking for clusters and gaps in the scores. which type of graph is the most appropriate?
Answers
Answer:
A histogram would be the most appropriate graph to display the distribution of scores and identify clusters and gaps.
Step-by-step explanation:
y = (3x)2 + 17
when x = 2
Answers
Answer:
y = 29
Step-by-step explanation:
y = (3x)2 + 17
y = (3(2))2 + 17
y = (6)2 + 17
y = 12 + 17
y = 29
In the number 8246315 what sigit is in the ones place
Answers
Answer:
5
Step-by-step explanation:
The ones place is the one most to the right that isn't after a decimal point.
Answer:
5, since it is all the way to the right
Step-by-step explanation:
if you ever have a big number, the number in thes ones place is ALWAYS on the far right, except if its a decimal !
i hope this helps !! :D
PLEASE HELP ME I DONT GET IT

Answers
Answer:
A) y = 2x
Step-by-step explanation:
How do I solve 4y-gon. The answer is 360(2y-1) but I don’t know how to show my work for it
Answers
Answer
search how they got the answer
Step-by-step explanation:
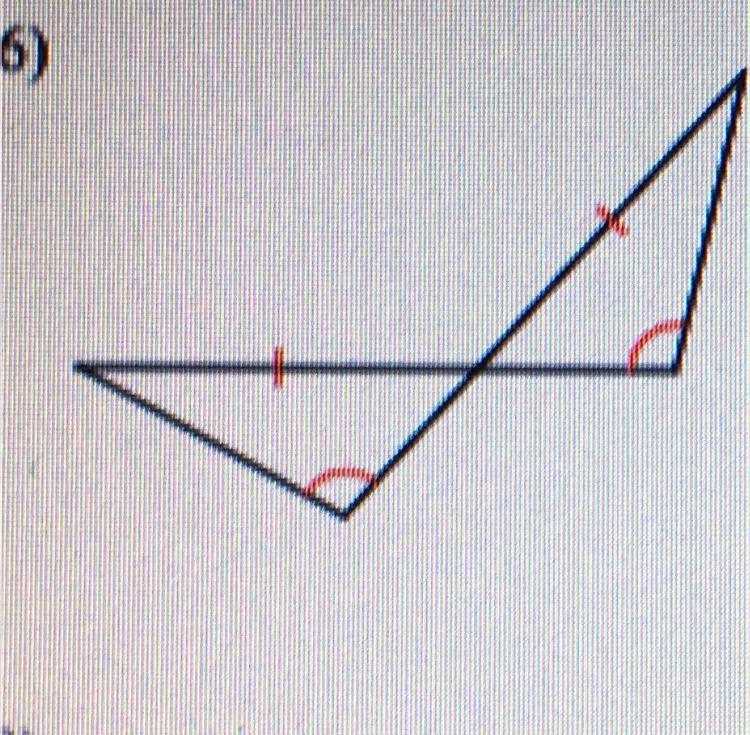
(SAT Prep) Find the value of x.
X
125°
115°

Answers
#look pic for detailed info
180° - 125° = 55°
180° - 115° = 65°
180° - 55° - 65° = 60°
180° - 60° = 120°
180° - 120° = 60°

Answer:
x = 120°
Step-by-step explanation:
you can draw a perpendicular base betweeen the two parallel segments and form a pentagon, which has 540 degrees inside.
the two base angles will each be 90°, and we have known values for the other two.
as far as 'x', that angle is vertical to the top angle of the pentagon so we add up all the known values and solve for 'x':
90 + 90 + 125 + 115 + x = 540
180 + 240 + x = 540
x = 540 - (180 + 240)
x = 540 - 420
x = 120
CKPenny is selling 50 coats. Each coat with a hood have 5 buttons and each coat without a hood have 10 buttons. If there are 400 buttons among all the coats, how many coats don't have hoods?
Answers
Answer:
40 coats don't have hoods