Describe the two possible outcomes of the test, using the context of the given situation. The governor claims that the percentage of adults over 21 who have graduated from high school is greater than 78%,the national average.
Answers
Answer:
The two possible outcomes of the test are accepting the governor's claim or rejecting it.
Step-by-step explanation:
To test the governor's claim, a hypothesis test can be conducted using a sample of adults over 21. The null hypothesis would be that the percentage of adults over 21 who have graduated from high school is equal to or less than 78%, while the alternative hypothesis would be that it is greater than 78%.
If the test results in a p-value that is smaller than the chosen significance level (typically 0.05), the null hypothesis would be rejected. This would mean that there is enough evidence to support the governor's claim that the percentage of adults over 21 who have graduated from high school is indeed greater than 78%.
On the other hand, if the test results in a p-value that is greater than the chosen significance level, the null hypothesis would be accepted. This would mean that there is not enough evidence to support the governor's claim, and it is possible that the percentage of adults over 21 who have graduated from high school is not greater than 78%.
Related Questions
Once again Plssssssss Help Meh


Answers
For the question of total area of the cuboid is 200cm^.
I understand where we divide 150 by 4.
But why do I need to multiply by 5, when there are 6 faces.
Answers
You need to multiply by 5 instead of 6 because each pair of opposite faces on a cuboid has the same area, so by considering one face from each pair, you ensure that you don't count any face twice.
When calculating the total surface area of a cuboid, you need to understand the concept of face pairs.
A cuboid has six faces, but each face has a pair that is identical in size and shape.
Let's break down the reasoning behind multiplying by 5 instead of 6 in the given scenario.
To find the surface area of a cuboid, you can add up the areas of all its faces.
However, each pair of opposite faces has the same area, so you avoid double-counting by only considering one face from each pair. In this case, you have five pairs of faces:
(1) top and bottom, (2) front and back, (3) left and right, (4) left and back, and (5) right and front.
By multiplying the average area of a pair of faces by 5, you account for all the distinct face pairs.
Essentially, you are considering one face from each pair and then summing their areas.
Since all the pairs have the same area, multiplying the average area by 5 gives you the total surface area.
When dividing 150 by 4 (to find the average area of a pair of faces), you are essentially finding the area of a single face.
Then, by multiplying this average area by 5, you ensure that you account for all five pairs of faces, providing the total surface area of the cuboid.
Thus, multiplying by 5 is necessary to correctly calculate the total surface area of the cuboid by accounting for the face pairs while avoiding double-counting.
For similar question on cuboid.
https://brainly.com/question/29568631
#SPJ8
A 10-foot ladder is leaning against a vertical wall. If the bottom of the ladder is being pulled away from the wall at the rate of 9 feet per second, at what rate is the area of the triangle formed by the wall, the ground, and the ladder changing, in square feet per second, at the instant the bottom of the ladder is 6 feet from the wall
Answers
Answer:
The area is changing at 15.75 square feet per second.
Step-by-step explanation:
The triangle between the wall, the ground, and the ladder has the following dimensions:
H: is the length of the ladder (hypotenuse) = 10 ft
B: is the distance between the wall and the ladder (base) = 6 ft
L: the length of the wall (height of the triangle) =?
dB/dt = is the variation of the base of the triangle = 9 ft/s
First, we need to find the other side of the triangle:
\(H^{2} = B^{2} + L^{2}\)
\( L = \sqrt{H^{2} - B^{2}} = \sqrt{(10)^{2} - B^{2}} = \sqrt{100 - B^{2}} \)
Now, the area (A) of the triangle is:
\( A = \frac{BL}{2} \)
Hence, the rate of change of the area is given by:
\( \frac{dA}{dt} = \frac{1}{2}[L*\frac{dB}{dt} + B\frac{dL}{dt}] \)
\( \frac{dA}{dt} = \frac{1}{2}[\sqrt{100 - B^{2}}*\frac{dB}{dt} + B\frac{d(\sqrt{100 - B^{2}})}{dt}] \)
\(\frac{dA}{dt} = \frac{1}{2}[\sqrt{100 - B^{2}}*\frac{dB}{dt} - \frac{B^{2}}{(\sqrt{100 - B^{2}})}*\frac{dB}{dt}]\)
\(\frac{dA}{dt} = \frac{1}{2}[\sqrt{100 - 6^{2}}*9 - \frac{6^{2}}{\sqrt{100 - 6^{2}}}*9]\)
\(\frac{dA}{dt} = 15.75 ft^{2}/s\)
Therefore, the area is changing at 15.75 square feet per second.
I hope it helps you!
The rate of change (ROC) of the area with respect to (w.r.t.) time can be
found from the ROC of the area w.r.t. x and the ROC of x w.r.t. time.
At the time the ladder is 6 feet from the wall, the area is increasing at 15.75 ft.²/sec.Reasons:
The length pf the ladder = 10 feet
Rate at which the ladder is pulled from the wall, \(\displaystyle \frac{dx}{dt}\) = 9 feet per second
Required:
The rate at which the area of the triangle formed by the ladder, the wall
and the ground, is changing at the instant the ladder is 6 feet from the wall.
Solution:
The area the triangle, A = 0.5·x·y
Where;
x = The distance of the ladder from the wall
y = The height of the ladder on the wall
By Pythagoras's theorem, we have;
10² = x² + y²
Which gives;
y = √(10² - x²)
Therefore;
The area the triangle, A = 0.5 × x × √(10² - x²)
By chain rule, we have;
\(\displaystyle \frac{dA}{dt} = \mathbf{\frac{dA}{dx} \times \frac{dx}{dt}}\)
\(\displaystyle \frac{dA}{dx} = \frac{d\left(0.5 \cdot x \cdot \sqrt{10^2 - x^2} }{dx} = \mathbf{\frac{\left(x^2 - 50\right) \cdot \sqrt{100-x^2} }{x^2-100}}\)
\(\displaystyle \frac{dA}{dx} = \frac{\left(x^2 - 50\right) \cdot \sqrt{100-x^2} }{x^2-100}\)
Therefore;
\(\displaystyle \frac{dA}{dt} = \mathbf{\frac{\left(x^2 - 50\right) \cdot \sqrt{100-x^2} }{x^2-100} \times 9}\)
When the ladder is 6 feet from the wall, we have;
x = 6
\(\displaystyle \frac{dA}{dt} = \frac{\left(6^2 - 50\right) \cdot \sqrt{100-6^2} }{6^2-100} \times 9 = \mathbf{15.75}\)
At the time the ladder is 6 feet from the wall, the area is increasing at 15.75 ft.²/sec.
Learn more about chain rule of differentiation here:
https://brainly.com/question/20341047
Identify the axis of symmetry, vertex, and range for the quadratic function.
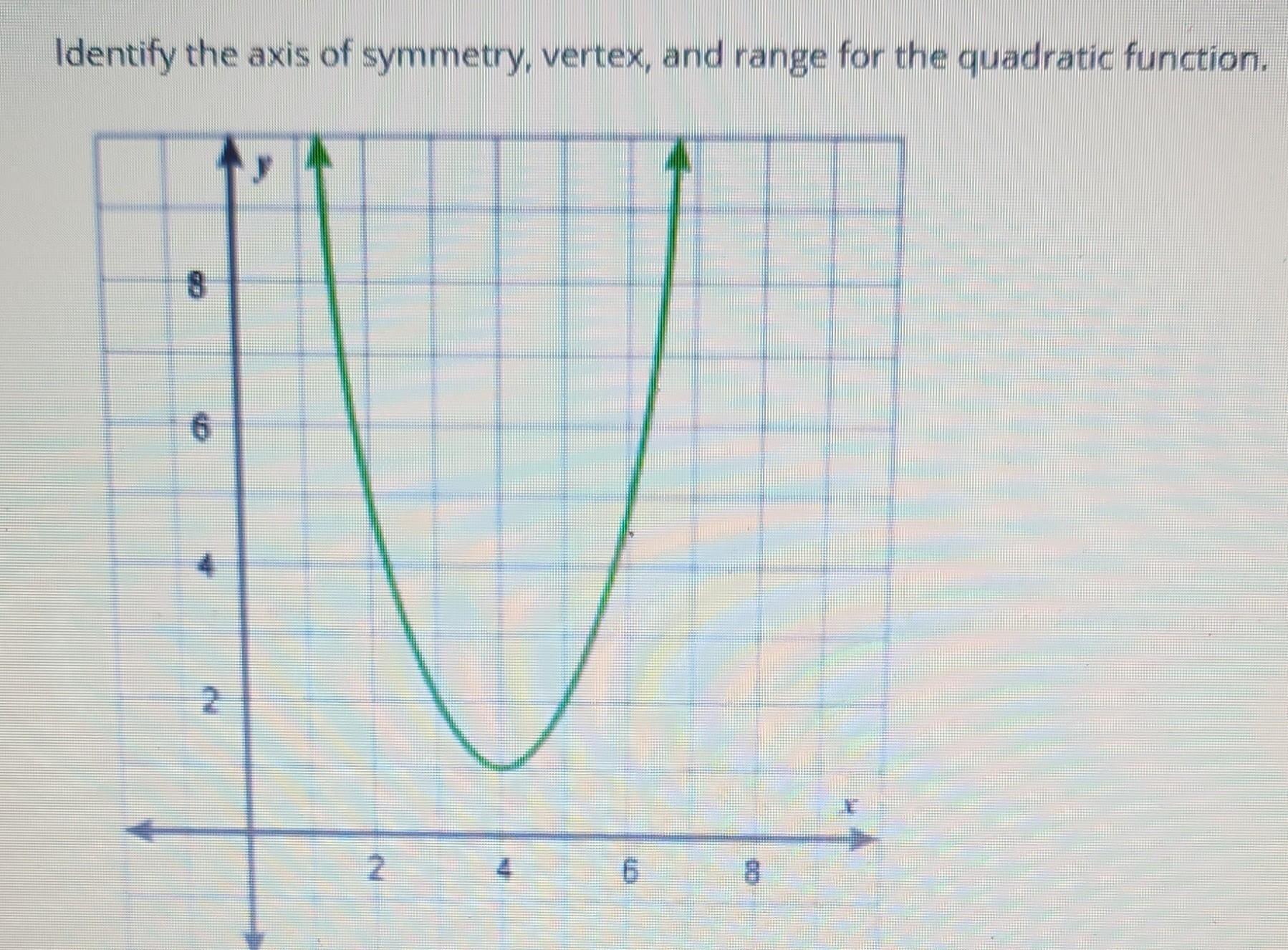
Answers
Use the distributive property to write an expression that is equivalent to:
3(x + 5)
Answers
Answer: 3x + 15
Step-by-step explanation:
In order to use the distributive property, you simply multiply the number on the outside by both the number inside the parenthesis
So, in this case, we would multiply 3 by X and 3 by 5
3 times x = 3x
3 times 5 =15
Your new equation is then made by adding these two together
3x+15
Answer 3x + 15
I WILL MARK BRIANLIEST PLEASE HELP!!!

Answers
Answer:
50 degrees
Step-by-step explanation:
Angle ABE is the opposite of the angle given on two converging lines, making it the same degree :)
Let X1, X2, X3 be mutually independent random variables with Poisson distributions having means 2, 1, and 4, respectively.
(a) Find the mgf of the sum Y = X1 + X2 + X3.
(b) How is Y distributed?
(c) Compute P(3 ≤ Y ≤ 9).
Answers
The sum Y = X1 + X2 + X3's mgf is 1 + 2X + 3X².
What is Independent variable?In statistical modeling, experimental sciences, and mathematical modeling, there are dependent and independent variables. Dependent variables are examined under the presumption or requirement that they are constrained by some rule or law to depend on the values of other variables. In an experimental study, an independent variable is a variable that you alter, regulate, or change to examine its effects. Because it is unaffected by any other study variables, it is referred to as being "independent." The term "explanatory variables" also applies to independent variables. The characteristic of an experiment that is altered or changed by researchers, as opposed to other experimental variables, is known as the independent variable (IV) in psychology.Given,
Y = X1 + X2 + X3.
\($\frac{d}{d X}\left(X^1+X^2+X^3\right)\)
Simplifying the above equation,
\($X^1+X^2+X^3: \quad X+X^2+X^3$\)
= \($\frac{d}{d X}\left(X+X^2+X^3\right)\)
=\($\frac{d}{d X}(X)+\frac{d}{d X}\left(X^2\right)+\frac{d}{d X}\left(X^3\right)\)
\($\frac{d}{d X}(X)=1\)
Simplifying,
\($\frac{d}{d X}\left(X^2\right)=2 X\)
\($\frac{d}{d X}\left(X^3\right)=3 X^2\)
Then we get,
= 1 + 2X + 3X²
To learn more about Independent variable, refer to:
https://brainly.com/question/25223322
#SPJ1
What is the perimeter of the triangle? (30 Points)

Answers
Answer:
D. 8x - 3
Step-by-step explanation:
Simply add all the sides up - 2x+3x+3x - 1+1+1 = 8x - 3
Given y=4x+2, find the domain value if the range value is 4
Answers
4-2=4x+2-2
2=4x
Divided both sides by 4
X=1\2
The domain value that corresponds to a range value of 4 is,
⇒ x = 1/2
Given that;
Function is,
y = 4x + 2
Since, the equation equal to the range value:
4 = 4x + 2
Then, we can solve for "x":
4 - 2 = 4x
2 = 4x
x = 1/2
Now that we have the value of "x", we can find the corresponding value of "y" by substituting it into the given equation:
y = 4x + 2
y = 4(1/2) + 2
y = 4 + 2
y = 6
Therefore, the domain value that corresponds to a range value of 4 is,
⇒ x = 1/2
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ1
Use mathematical induction to prove the following statement:
The sum of the first n even positive integers is (n2 + n). That is, 2 4 6 8 .... 2n
Answers
Answer:
Step-by-step explanation:
To prove that the sum of the first n even +ve integers is:
\(\mathsf{2+4+6+8+ . . . +2n = n^2+ n }\)
By using mathematical induction;
For n = 1, we get:
2n = 2 × 1 = 2
2 = 1² + 1 ----- (1)
∴ the outcome is true if n = 1
However, let assume that the result is also true for n = k
Now, \(\mathsf{2+4+6+8+. . .+2k = k^2 + k --- (2)}\)
\(\mathsf{2+4+6+8+. . .+2k+2(k+1)}\)
we can now say:
\(\mathsf{= (k^2 + k) + 2(k + 1)} \\ \\ \mathsf{= k^2 + k + 2k + 1}\)
\(\mathsf{= (k^2 + 2k + 1) + (k + 1)}\)
\(\mathsf{= (k + 1)^2 + (k + 1)}\)
∴
\(\mathsf{2 + 4 + 6 + 8 + . . . + 2k + 2(k + 1) = (k + 1)^2 + (k + 1)}\)
Thus, the result is true for n = m+1, hence we can posit that the result is also true for each value of n.
As such \(\mathsf{2+4+6+8+. . .+2n = n^2 + n }\)
The U.S. Department of Energy's Fuel Economy Guide provides fuel efficiency data for cars and trucks (U.S. Department of Energy website, February 22, 2008). A portion of the data for 311 compact, midsize, and large cars follows. The column labeled Class identifies the size of the car; Compact, Midsize, or Large. The column labeled Displacement shows the engine's displacement in liters. The column labeled Fuel Type shows whether the car uses premium (P) or regular (R) fuel, and the column labeled HwyMPG shows the fuel efficiency rating for highway driving in terms of miles per gallon.
a) Develop an estimated regression equation that can be used to predict the fuel efficiency for highway driving, given the engine's displacement.
Let x represent the engine's displacement.
If required, round your answers to four decimal places. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300)
Y = ___ + ___ x
b) How much of the variation in the sample values of HwyMPG does this estimated regression equation explain?: ____%
c) Consider the addition of the dummy variables ClassMidsize and ClassLarge to the simple linear regression model in part (a). The value of ClassMidsize is 1 if the car is a midsize car and 0 otherwise; the value of ClassLarge is 1 if the car is a large car and 0 otherwise. Thus, for a compact car, the value of ClassMidsize and the value of ClassLarge are both 0. Develop the estimated regression equation that can be used to predict the fuel efficiency for highway driving, given the engine's displacement and the dummy variables ClassMidsize and ClassLarge. Let x1 represent engine's displacement. Let x2 represent variable ClassMidsize. Let x3 represent variable ClassLarge.If required, round your answers to four decimal places. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300)
Y = ___ + ___ x1 + ___ x2 + ___ x3
d) How much of the variation in the sample values of HwyMPG does this estimated regression equation explain? : ___ %
e) Consider the addition of the dummy variable FuelPremium, where the value of FuelPremium is 1 if the car uses premium fuel and 0 if the car uses regular fuel. Develop the estimated regression equation that can be used to predict the fuel efficiency for highway driving, given the engine's displacement, the dummy variables ClassMidsize and ClassLarge, and the dummy variable FuelPremium. Let x1 represents engine's displacement. Let x2 represents variable ClassMidsize. Let x3 represents variable ClassLarge. Let x4 represents variable FuelPremium. If required, round your answers to four decimal places. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300)
Y = ___ + ___ x1 + ___ x2 + ___ x3 + ___x4
f) How much of the variation in the sample values of HwyMPG does this estimated regression equation explain? : ___ %
Answers
a) Y=38.6594-5.4198x; b) 39.1% explained variation; c) Y=44.9379-5.9522x1-1.2758x2-2.0102x3; d) 49.9% explained variation; e) Y=45.2478-6.1081x1-0.9945x2-2.5692x3+0.9963x4; f) 53.1% .
a) The estimated regression equation for predicting fuel efficiency for highway driving is Y = 38.6594 - 5.4198x, where x represents the engine's displacement in liters.
b) The estimated regression equation explains 39.1% of the variation in the sample values of HwyMPG.
c) The estimated regression equation that includes the dummy variables ClassMidsize and ClassLarge is Y = 44.9379 - 5.9522x1 - 1.2758x2 - 2.0102x3, where x1 represents engine's displacement, x2 represents variable ClassMidsize, and x3 represents variable ClassLarge.
d) The estimated regression equation with the added dummy variables explains 49.9% of the variation in the sample values of HwyMPG.
e) The estimated regression equation that includes the dummy variable FuelPremium is Y = 45.2478 - 6.1081x1 - 0.9945x2 - 2.5692x3 + 0.9963x4, where x1 represents engine's displacement, x2 represents variable ClassMidsize, x3 represents variable ClassLarge, and x4 represents variable FuelPremium.
f) The estimated regression equation with all three dummy variables explains 53.1% of the variation in the sample values of HwyMPG.
Learn more about equation here:
https://brainly.com/question/13763238?
#SPJ4
I need help with this question please

Answers
The probability that the mean height of a random sample of 56 ten-year-old males will be greater than 53 inches is approximately 0.9991, or 99.91% when rounded to three decimal places.
What is the central limit theorem?
The central limit theorem, which states that the sample means of large samples (n > 30) from a population with any distribution approaches a normal distribution with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.
We can solve this problem by using the central limit theorem,
In this case, the sample size is n = 56, which is larger than 30, so we can assume that the sample means are normally distributed. The mean of the sample means is equal to the population mean, which is 55.5 inches, and the standard deviation of the sample means is equal to the population standard deviation divided by the square root of the sample size:
standard deviation = 6 / √(56) = 0.801
To find the probability that the mean height of the sample will be greater than 53 inches, we can standardize the sample mean using the standard deviation calculated above:
z = (sample mean - population mean) / (standard deviation)
= (53 - 55.5) / 0.801
= -3.12
Using a standard normal distribution table or calculator, we can find the probability that a standard normal random variable is greater than -3.12:
P(Z > -3.12) = 0.9991 (rounded to four decimal places)
Therefore, the probability that the mean height of a random sample of 56 ten-year-old males will be greater than 53 inches is approximately 0.9991, or 99.91% when rounded to three decimal places.
To learn more about the central limit theorem visit,
https://brainly.com/question/18403552
#SPJ1
andy’s saving account pays 0.3% more interest then marty’s. martys account earns 200 in interest. how much does interest does andy’s account earn?
1. 200.60
2. 203.00
3. 206.00
4. 230.00
Answers
200.60 interest does andy’s account earn.
Let x be the amount of interest earned by Andy's account.
According to the problem, Andy's account earns 0.3% more interest than Marty's account, which means that Andy's account earns the same amount plus an additional 0.3% of that amount. Mathematically, we can express this as:
x = 200 + 0.3% of 200
Simplifying the right-hand side of the equation, we get:
x = 200 + 0.003 × 200
x = 200.60
Therefore, the answer is option 1: 200.60.
Learn more about Percentage here:
https://brainly.com/question/29306119
#SPJ1
based on the graph how many tiles are im figure 0

Answers
For figure {0}, the number of tiles will be equal to 2.
What is a mathematical function, equation and expression?Function : In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function
Expression : A mathematical expression is made up of terms (constants and variables) separated by mathematical operators
Equation : A mathematical equation is used to equate two expressions.
Given is a graph as shown in the image.
The line passes through point -
(3, 8) and (4, 10)
So, the slope of the line will be -
m = (10 - 8)/(4 - 3)
m = 2
y = 2x + c
For the point (3, 8), we can write -
8 = 6 + c
c = 2
For figure {0}, the number of tiles will be equal to 2.
Therefore, for figure {0}, the number of tiles will be equal to 2.
To solve more questions on functions, expressions and polynomials, visit the link below -
brainly.com/question/17421223
#SPJ1
combine like terms
8x+3-5x+9
a. 3x+12
b.-13x-12
c.13x+12
d.3x-6

Answers
Answer:
A. 3x+12
Step-by-step explanation:
8x+3-5x+9
8x-5x=3x
3+9=12
then put them together
3x+12
answer= A
A one dimensional object with no endpoint is a?
A.ray
B.line segment
C.line
D.point
Answers
Answer:
its line fjfjfjjejjdjdj
As per the given condition, the required one dimensional object with no end point is a line.
What is a ray?"In geometry, a ray can be defined as a part of a line that has a fixed starting point but no end point. It can extend infinitely in one direction.
On its way to infinity, a ray may pass through more than one point. When naming a ray, it is denoted by drawing a small ray on top of the name of the ray. "
What is a line segment?"A line segment is a part of a line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints."
What is a line?"A line is a one-dimensional object, which has length but no width. A line is made of a set of points which is extended in opposite directions infinitely. It is determined by two points in a two-dimensional plane. "
What is a point?"A point is a primitive notion that models an exact location in the space, and has no length, width, or thickness. In modern mathematics, a point refers more generally to an element of some set called a space."
Given, a one dimensional object with no endpoint.
Therefore, the require object is a line.
Learn more about a line here: https://brainly.com/question/27560536
#SPJ2
Which term of the sequence 1/4;-1;-21/4;...is equal to -131/2
Answers
11, - 6, -1, 4, 9, 14, 19, ... are mapped onto 4. ... A;-l = (-ltQn (mod N),. (A5.34) ... 131 2, 14, 34, 38, 42, 78, 90, 178, 778, 974(1000).
Step-by-step explanation:
the nearest .1/2 incp, we say the 'unit 131/2 incl. 1.4 a measUrement is-stated tp- be 546 inch, this UM= the
Linear equation: -1 2 (6x + 10) = 13 Step 1: –3x – 5 = 13 Step 2: –3x = 18 Step 3: x = –6 Which sequence describes the inverse operations used for steps 2 and 3 to solve the linear equation? the addition property of equality and then the division property of equality the addition property of equality and then the multiplication property of equality the subtraction property of equality and then the division property of equality the subtraction property of equality and then the multiplication property of equality
Answers
Answer:
(A) the addition property of equality and then the division property of equality
Step-by-step explanation:
To get from Step 1 to Step 2, we have added 5 to both sides of the equation:
-3x -5 +5 = 13 +5
-3x = 18
To get from Step 2 to Step 3, we have divided both sides of the equation by -3:
-3x/-3 = 18/-3
x = -6
These operations can be described as ...
the addition property of equality and then the division property of equality
__
However, since addition and subtraction are the same thing, but with opposite numbers, and since multiplication and division are the same thing, but with reciprocal numbers, any of the answer choices is arguably correct.
(add 5, divide by -3) = (add 5, multiply by -1/3) =
(subtract -5, divide by -3) = (subtract -5, multiply by -1/3)
Answer:
A.) the addition property of equality and then the division property of equality
Step-by-step explanation:
Got It Right. Trust me
if 1 centimeter=0.3937 inches, use dimensional analysis to find 2.4 meters in yards. Round to the nearest hundredth. (hint: 1yd=36in)
Answers
Step-by-step explanation:
We know from the problem that:
1 centimeter = 0.3937 inches
1 yard = 36 inches
I suggest that we convert the starting length of 2.4 meters to centimeters, and from there we could convert to inches, and then convert to yards.
\(\frac{2.4\ meters}{}|\frac{100\ centimeters}{1.0\ meters} |\frac{0.3937\ inches}{1.0\ centimeters} |\frac{1.0\ yards}{36\ inches}\)
\(=(2.4)(\frac{100}{1.0})(\frac{0.3937}{1.0})(\frac{1.0}{36})\)
\(=(\frac{(2.4)(100)(0.3937)}{36})yards\)
\(=2.62\ yards\)
-25 greater than 10 P
Answers
Answer:
10P-25
Step-by-step explanation:
Answer: -25 is not greater than 10 :P
Solving a word problem on proportions using a unit rate
Dante drove 871 miles in 13 hours.
At the same rate, how long would it take him to drive 603 miles?
Answers
The unit rate of miles per hour is:
871 miles ÷ 13 hours = 67 miles per hour
This means that Dante drove at a rate of 67 miles per hour.
To find out how long it would take him to drive 603 miles at the same rate, we can set up a proportion:
871 miles ÷ 13 hours = 603 miles ÷ x hours
We can cross-multiply to solve for x:
871x = 13 * 603
871x = 7,839
x = 9
Therefore, it would take Dante 9 hours to drive 603 miles at the same rate of 67 miles per hour.
Show that an implicit solution of 2x sin2(y) dx − (x2 + 10) cos(y) dy = 0 is given by ln(x2 + 10) + csc(y) = C. Differentiating ln(x2 + 10) + csc(y) = C we get 2x x2 + 10 + dy dx = 0 or 2x sin2(y) dx + dy = 0. Find the constant solutions, if any, that were lost in the solution of the differential equation. (Let k represent an arbitrary integer.)
Answers
Answer:
Step-by-step explanation:
\(2xsin(2y)dx-(x^2+10) cosy dy =0\\\\\frac{2x}{x^2 + 10}dx= \frac{cosy}{sin(2y)}\)
Take integration both side (apply substitution for the left hand side, apply sin(2y) = 2 sin(y) cos(y) for the right hand side) you will have the condition.
Problem solved
5(9+d) -6 when d=3 hjvbvb
Answers
Hey there!
If d = 3 then substitute where “d” is at, now let’s work out the equation!
5(9 + 3) – 6
• DISTRIBUTE:
5(9) + 5(3)
5(9) = 45
5(3) = 15
• NEW EQUATION:
45 + 15 – 6
45 + 15 = 60
60 – 6 = 54
Answer: 54 ☑️
Good luck on your assignment and enjoy your day!
~LoveYourselfFirst:)
SIDE NOTE:
You could use PEMDAS to solve this as well.
Here’s what it means ⬇️
• Parentheses
• Exponent
• Multiplication
• Division
• Addition
• Subtraction
5(12)-6
60-6
54
Please give brainliest!!
does 2, 5, and 7 make a right triangle
Answers
Answer: No, we don't have a right triangle
==========================================================
Explanation:
If a triangle with sides a,b,c makes the equation a^2+b^2 = c^2 true, where c is the longest side, then this triangle is a right triangle. This is the converse of the pythagorean theorem.
Here we have a = 2, b = 5 and c = 7.
So...
a^2+b^2 = c^2
2^2+5^2 = 7^2
4+25 = 49
29 = 49
The last equation is false, so the first equation is false for those a,b,c values. Therefore, we do not have a right triangle.
------------
In contrast, consider the classic 3-4-5 right triangle
a = 3, b = 4 and c = 5 would make a^2+b^2 = c^2 true because 3^2+4^2 = 5^2 is a true equation (both sides lead to 25).
Need help with this question pls due today!!!!

Answers
Answer:
Step-by-step explanation:
area of circle=π*r^2
=3.14*2.5^2
=3.14*6.25
=19.625
=19.63
So the answer is 19.625
I need Help please!!!

Answers
Step-by-step explanation:
it seems you solved the tricky part yourself already.
just to be sure, let's do the first derivative here again.
the easiest way would be for me to simply multiply the functional expression out and then do a simple derivative action ...
f(t) = (t² + 6t + 7)(3t² + 3) = 3t⁴ + 3t² + 18t³ + 18t + 21t² + 21 =
= 3t⁴ + 18t³ + 24t² + 18t + 21
f'(t) = 12t³ + 54t² + 48t + 18
and now comes the simple part (what was your problem here, don't you know how functions work ? then you are in a completely wrong class doing derivatives; for that you need to understand what functions are, and how they work). we calculate the function result of f'(2).
we simply put the input number (2) at every place of the input variable (t).
so,
f'(2) = 12×2³ + 54×2² + 48×2 + 18 = 96 + 216 + 96 + 18 =
= 426
determine the intercepts of the line

Answers
Answer:
y- (0,2.5) x-(3.5,0)
Step-by-step explanation:
This is because the intercepts of a graph are the points at which a line intersects with a desired axis. So for the Y axis the inercept would be at 2.5 making the y intercept (0,2.5). The same concept is used on the X axis.
Using the order of operations and locations of parentheses (brackets), change the value
of a string of four 4s to evaluate to 36
Answers
Answer:
4 ( 4 + 4 + 4 )
Step-by-step explanation:
There are 15 pieces of fruit in a bowl and 6 of them are apples. What
percentage of the pieces of fruit in the bowl are apples?
O 0.06%
O 0.4%
O 6%
40%
Answers
Answer:
40%.
Step-by-step explanation:
There are 6 / 15 apples out of the bowl.
6/15 = 2/5 = 0.4
So, 40% of the fruit in the bowl are apples.
Hope this helps!
Identify a set of parallel lines and a set of perpendicular lines in this image. Please help

Answers
Answer:
line AB and line CD are parallel
line AB and line EF are perpendicular
Step-by-step explanation:
it is the third option