At the end of any year a car is worth 5% less than what is was worth at the beginning of the year. if a car was brought for 10 000 in January 2009, its value in December 2009 was

The global min and max of the function f(x, y) = 3y - 2x², on the region bounded is global maximum value is 1,

Given the function f(x, y) = 3y - 2x².

The region is bounded by the line y=x and the parabola y = x² + x - 1.

Therefore, the extreme values of the function f(x, y) = 3y - 2x² are either on the boundary of the region or at critical points inside the region. Let's start by finding the boundary points for this problem.

Boundary Points: We know that the region is bounded by y = x²+x-1 and y = x. Setting the two equations equal to each other to find their intersection points, we have:x² + x - 1 = x.

Rearranging the equation, we get:x² - 1 = 0. Solving for x, we have:x = ±1.Now, plugging these values into y = x, we get two boundary points, which are: (1, 1) and (-1, -1).

Let's evaluate f(x, y) = 3y - 2x² at these two points to find the maximum and minimum values:

At (1, 1):f(1, 1) = 3(1) - 2(1)² = 1.At (-1, -1):f(-1, -1) = 3(-1) - 2(-1)² = -1.

Therefore, the global maximum value is 1, which occurs at (1, 1), and the global minimum value is -1, which occurs at (-1, -1).

Hence, the global min and max of the function f(x, y) = 3y - 2x², on the region bounded by y = x²+x-1 and the line y=x is global maximum value is 1, which occurs at (1, 1), and the global minimum value is -1, which occurs at (-1, -1).

Know more about the global maximum

https://brainly.com/question/13602432

#SPJ11

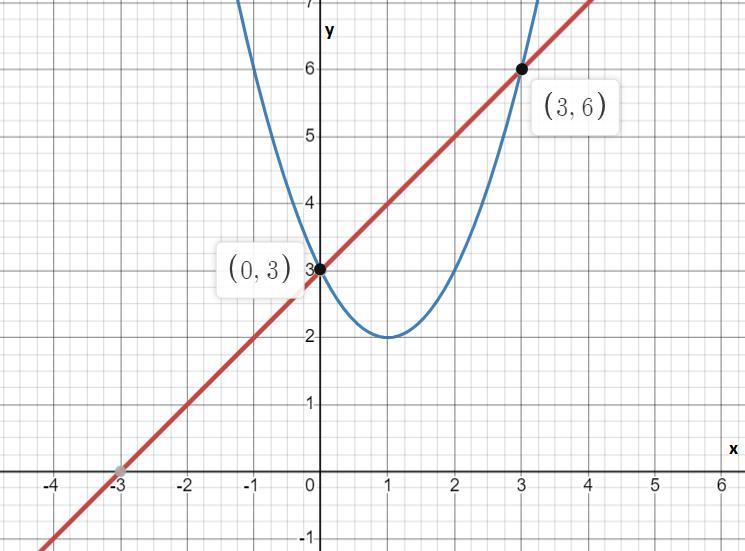
The solution to the system of equations y = x² - 2x + 3 is given as follows:

(0,3) and (3,6).

The equations for this problem are given as follows:

We solve the system graphically, hence the solution is given by the point of intersection of the graphs of the two functions.

From the graph given by the image presented at the end of the answer, the two solutions are given as follows:

(0,3) and (3,6).

More can be learned about a system of equations at https://brainly.com/question/13729904

#SPJ1

Answer:

False. The two figures are not similar.

Step-by-step explanation:

For two polygons to be similar, the ratios of pairs of corresponding sides must all be equal.

MQ/GH = 1, PQ/EH = 2, so MQ/GH does not equal PQ/EH. So these two figures are not similar.

Answer:

Interior: 135 degrees

Exterior: 45 degrees

Step-by-step explanation:

The interior angle of a regular octagon is exactly 135 degrees, which can be found using the (n – 2)180 formula. The exterior is simply 180 - the interior, which is 45. :)

Answer:

whadda say

Step-by-step explanation:

interior angle: (n-2)×180°

exterior angle: (n-2)÷180°

The statement "P implies Q" is false under the following conditions: a) P is true and Q is false, and d) P is false and Q is true.

The statement "P implies Q" can be expressed as "if P, then Q." It is a conditional statement where P is the antecedent (the condition) and Q is the consequent (the result).

To determine when the statement is false, we need to identify cases where P is true but Q is false, or when P is false but Q is true.

Option a) states that both P and Q are true. In this case, the statement "P implies Q" holds true because if P is true, then Q is true.

Option b) states that both P and Q are false. In this case, the statement "P implies Q" is considered true because the antecedent (P) is false.

Option c) states that P is true and Q is false. Under this condition, the statement "P implies Q" is false because when P is true, but Q is false, the implication does not hold.

Option d) states that P is false and Q is true. In this case, the statement "P implies Q" is true because the antecedent (P) is false.

Therefore, the conditions under which the statement "P implies Q" is false are a) P is true and Q is false, and d) P is false and Q is true.

Learn more about conditional statement here:

https://brainly.com/question/30612633

#SPJ11

D. not continuous at X=0

if you trace the function you'll find a jump in the graph. To be continuous the line can't have any breaks in it. In this example, it's discontinuous when X=0

Percent change = change in value/original value.

13) 75 -> 38:  37 decrease/75 original

       49.3333333333333% decrease

       about 49% decreaase

14) 97 -> 3: 94 decreace/97 original

      96.9072164948454% decrease

      about 97% decrease

15) 77 -> 55: 22 decrease/77 original

      28.5714285714286% decrease

      about 29% decrease

16) 67 -> 28: 39 decrease/67 original

      58.2089552238806% decrease

      about 58% decrease

The increase in weekly wages for both the man and the boy is Rs. 40.

Let's assume that the increase in wages for both the man and the boy is x.

After the increase, the man's weekly wage will be Rs. 80 + x and the boy's weekly wage will be Rs. 35 + x.

We know that the man's wage after the increase is 8/5 of the boy's wage after the increase. Mathematically,

80 + x = (8/5)(35 + x)

Simplifying this equation, we get:

80 + x = 56 + (8/5)x

Multiplying both sides by 5, we get:

400 + 5x = 280 + 8x

Subtracting 5x from both sides, we get:

400 = 280 + 3x

Subtracting 280 from both sides, we get:

120 = 3x

Dividing both sides by 3, we get:

x = 40

Therefore, the increase in wages is Rs. 40.

To know more about weekly wages:

https://brainly.com/question/28754816

#SPJ4

Answer:

40 min per period

Step-by-step explanation:

When it has 8 periods :

Total time = 45 min per period for 8 period

Total time = 45 × 8 min

When it has 9 periods : let each period be of x min

Total time = x min per period for 9 period

Total time = x × 9 min

As total time remains same,

45 × 8 = x × 9

5 x 8 = x

40 = x

The vector equation for the line is:

r(t) = (1, 0, 6) + t(-4, 1, 4)

The parametric equations for the line.

x(t) = 1 - 4t

y(t) = t

z(t) = 6 + 4t

To find a vector equation and parametric equations for the line passing through the point (1, 0, 6) and perpendicular to the plane x + 4y + z = 7, we can first determine the direction vector of the line.

The normal vector of the plane x + 4y + z = 7 is (1, 4, 1) since the coefficients of x, y, and z represent the normal vector.

Any line perpendicular to this plane must have a direction vector orthogonal to the normal vector of the plane.

Let's call the direction vector of our line (a, b, c).

We know that the dot product of the direction vector and the normal vector of the plane is zero:

(a, b, c) ⋅ (1, 4, 1) = 0

This equation gives us a condition for the direction vector.

We can choose any values for a, b, and c as long as they satisfy this condition.

For simplicity, we can choose a = -4, b = 1, and c = 4, which gives us a direction vector (-4, 1, 4) orthogonal to the plane.

Now, let's denote the position vector of the given point (1, 0, 6) as (x₀, y₀, z₀) = (1, 0, 6).

The vector equation of the line can be written as:

r(t) = r₀ + t × v

where r₀ is the position vector of a point on the line (which is (1, 0, 6)), t is the parameter, and v is the direction vector of the line (-4, 1, 4).

Therefore, the vector equation for the line is:

r(t) = (1, 0, 6) + t × (-4, 1, 4)

Expanding this equation, we get:

x(t) = 1 - 4t

y(t) = t

z(t) = 6 + 4t

These are the parametric equations for the line passing through the point (1, 0, 6) and perpendicular to the plane x + 4y + z = 7.

Learn more about vector equation and parametric equations click;

https://brainly.com/question/30550663

#SPJ4

The volume generated by rotating the region bounded by the curves y = x and x = 4y about the axis x = 17 can be found using the method of cylindrical shells.

To start, let's consider a vertical strip in the region, parallel to the y-axis, with a width dy. As we rotate this strip around the axis x = 17, it creates a cylindrical shell. The radius of each shell is given by the distance between the axis of rotation (x = 17) and the curve y = x or y = x/4, depending on the region. The height of each shell is given by the difference between the curves y = x and y = x/4.

We can express the radius as r = 17 - y and the height as h = x - x/4 = 3x/4. The circumference of each cylindrical shell is given by 2πr, and the volume of each shell is given by 2πrhdy. Integrating the volumes of all the shells over the appropriate range of y will give us the total volume.

By setting up and evaluating the integral, we can find the volume generated by rotating the region about the axis x = 17 using the method of cylindrical shells.

Learn more about parallel here: https://brainly.com/question/31454782

#SPJ11

Answer:

5 m/s^2

Step-by-step explanation:

Force = mass x acceleration

f = ma

We have the force of 10 N and the mass of 2 kg.

10 N = 2 kg a

divide by 2 on both sides to isolate the a

a = 5 m/s^2

Answer:

\(\boxed {\boxed {\sf a= 5 \ m/s^2}}\)

Step-by-step explanation:

The formula for force is:

\(F=m*a\)

If we rearrange the formula for acceleration (a) and divide both sides by m we get:

\(\frac{F}{m}=a\)

The net force is 10 Newtons. Let's convert the units to make the problem easier later on.

The mass is 2 kilograms.

\(F=10 \ kg*m/s^2\\m= 2 \ kg\)

Substitute the values into the formula.

\(\frac{10 \ kg*m/s^2}{2 \ kg} =a\)

Divide. Note the kilograms (kg) will cancel each other out (this is why we converted the units)

\(\frac{10 \ m/s^2}{2}=a\)

\(5 \ m/s^2=a\)

The acceleration of the box is 5 meters per second squared.

Answer:

C

Step-by-step explanation:

Answer:

Hi^^^its Anime

What is the range of this relashinship for

(17, 1)

(12, -19)

(7, 4)

(17, 11)

Would be  (-17, 7, 12, 17) known as b).

Step-by-step explanation:

Step-by-step explanation:

The numbers are given as;

100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125

What is the probability of getting;

a) A number 108?

Probability = Number of favorable outcomes / Total number of outcomes

Number of favourable outcome = 1

Total number of outcomes = 26

Probability = 1 / 26

B) a number less than 107

Probability = Number of favorable outcomes / Total number of outcomes

Number of favourable outcome = 100, 101, 102, 103, 104, 105, 106 = 7

Total number of outcomes = 26

Probability = 7 / 26

c) A number greater than 120

Probability = Number of favorable outcomes / Total number of outcomes

Number of favourable outcome = 121, 122, 123, 124, 125 = 5

Total number of outcomes = 26

Probability = 5 / 26

Answer:

hi

Step-by-step explanation:

i think it is 90⁰

have a nice day

D. 90°

90°

All four inner angles of a square are the same (each being 360°/4 = 90°, a right angle). The central angle of a square is equal to 90° (360°/4). The external angle of a square is equal to 90°.

the total interior angles of a square are 360°.

The sum of exterior angles in a polygon is usually equal to 360 degrees. therefore, for all equiangular polygons, the degree of one outdoors perspective is equal to 360 divided by the number of sides in the polygon.

Learn more about the angle of a square here

https://brainly.com/question/15847876

#SPJ2

(a) By plugging in different values for x1, we can plot the indifference curves passing through the given points (2, 2), (1, 2), and (4, 2).

(b) The shape of the indifference curves shows convexity.

(c) The property used to determine this is the non-satiation property of preferences.

(d) The Walrasian demand may not always be single-valued.

(e) Receiving the voucher makes the consumer better-off .

(f) The cash payment allows the consumer to maximize utility by making trade-offs

For 4x1 + x2 = x1 + 2x2, rearranging the equation gives x2 = 3x1, representing the linear part of the indifference curves.

For x1 + 2x2 = 4x1 + x2, rearranging the equation gives x2 = 3x1, representing the kink in the indifference curves.

By substituting different values for x1, we can plot the indifference curves. They will be upward sloping straight lines with a kink at x2 = 3x1.

(b) Properties of the preferences deduced from the shape of indifference curves and utility function:

Diminishing Marginal Rate of Substitution (MRS): Indifference curves are convex, indicating diminishing MRS. The consumer is willing to give up less of one good as they consume more of it, holding the other good constant.

Non-Satiation: Indifference curves slope upwards, showing that the consumer prefers more of both goods. They always prefer bundles with higher quantities.

Convex Preferences: The kink in the indifference curves indicates convexity, implying risk aversion. The consumer is willing to trade goods at different rates depending on the initial allocation.

(c) UMP does not have a solution when Pk = 0 and X -> R2+. This violates the assumption of finite resources and prices required for utility maximization. The property used is non-satiation, as a consumer will always choose an infinite quantity of goods when they are available at zero price.

(d) Walrasian demand depends on relative prices:

If p1 = p2 > 4, the maximizing bundle lies on the linear portion of indifference curves, where x2 = 3x1.

If 4 < p1 = p2 < 1/2, the maximizing bundle lies on the linear portion of indifference curves but at lower x1 and x2.

If p1 = p2 < 1/2, the maximizing bundle lies at the kink point where x1 = x2.

Walrasian demand may not be single-valued due to the shape of indifference curves and the kink point, allowing for multiple optimal solutions based on relative prices.

(e) Given p1 = p2 = 1 and w = $60, the initial budget set is x1 + x2 = 60. With a $10 voucher for good 1, the new budget set becomes x1 + x2 = 70. Since p1 = 1, the consumer spends the voucher on good 1, resulting in x1 = 20 and x2 = 40. Receiving the voucher improves the consumer's welfare by allowing more consumption of good 1 without reducing good 2.

(f) If given the choice between a $10 cash payment and a $10 voucher for good 1 only, the consumer would choose the cash payment. It provides flexibility to allocate the funds based on individual preferences. The answer remains the same even if the assistance were $30, as the cash payment still allows optimal allocation based on preferences. Cash payment offers greater utility-maximizing options compared to the voucher, which restricts choices.

To know more about indifference curves, visit;
https://brainly.com/question/32705949

#SPJ11

The answers that describe the quadrilateral DEFG area rectangle and parallelogram.

The correct answer choice is option A and B.

A quadrilateral is a parallelogram, which has opposite sides that are congruent and parallel.

Quadrilateral DEFG

if line DE || FG,

line EF // GD,

DF = EG and

diagonals DF and EG are perpendicular,

then, the quadrilateral is a parallelogram

Hence, the quadrilateral DEFG is a rectangle and parallelogram.

Read more on quadrilaterals:

https://brainly.com/question/23935806

#SPJ1

Answer:

 xy

---------

x + y

Step-by-step explanation:

(xy)

-----  is in its simplest form.

(x + y)

I hope this helps!

A used book store also started selling used CDs and videos. In the first week, the store sold 40 used CDs  then 30 CDs and 10 Videos were sold.

Given that a used book store also started selling used CDs and videos. In the first week, the store sold 40 used CDs and videos, at 4.00 per CD and 6.00 per video.

The sales for both CDs and videos totaled to 180.00.

Let CDs be x and Videos be y

Then we have x+y =3040

and 4x+6y = 180

Two simultaneous equations in two variables and can be solved by elimination method

multiply I equation by 4 and subtract from II.

2y = 20

y =10

x = 30

30 CDs and 10 Videos were sold.

learn more about of equation here

https://brainly.com/question/14586188

#SPJ4

Answer:

196 miles

Step-by-step explanation:

distance (D) is calculated as

D = S × T ( S is average speed and T is time in hours )

here T = 3 and a half hours = 3.5 hours and S = 56 , then

D = 56 × 3.5 = 196 miles

y = -5x – 24 is an equation of the line paing through the given point. (1, -14) and (-2,10)

Using the point-slope form of the equation of a line:

y - y1 = m(x - x1)

We can substitute the given points with their coordinates:

y - (-14) = m(x - 1)

and

y - 10 = m(x + 2)

We can solve for m:

y - (-14) = m(x - 1)

y - 10 = m(x + 2)

Subtract the second equation from the first:

y - (-14) - (y - 10) = m(x - 1) - m(x + 2)

-24 = -m(x - 1) - m(x + 2)

-24 = -2mx - m

Divide both sides by -2m:

24/-2m = mx + m/-2m

-12/m = x + 1/2

Substitute -12/m for x in the first equation:

y - (-14) = m(-12/m - 1)

y - (-14) = -12 - m

Add 14 to both sides:

y = -12 - m + 14

y = -12 - m + 14

Combine like terms:

y = -m - 12

The equation of the line is y = -m - 12. We can find m by substituting any of the given points into the equation:

y = -m - 12

Substitute (1, -14):

-14 = -m - 12

Add 12 to both sides:

-2 = -m

Divide both sides by -1:

m = 2

Therefore, the equation of the line is y = -5x - 24.

Learn more about equation here

https://brainly.com/question/29657992

#SPJ4

The chocolate for 140 bon-bons would cost approximately $6.13.

1. Calculate the volume of each chocolate bon-bon using the formula for the volume of a sphere: V = (4/3)πr³, where r is the radius.

  V = (4/3)π(0.7 cm)³

  V ≈ 1.437 cm³

2. Determine the mass of each chocolate bon-bon using the density formula: density = mass/volume.

  density = 1.27 g/cm³

  mass = density * volume

  mass ≈ 1.27 g/cm³ * 1.437 cm³

  mass ≈ 1.826 g

3. Calculate the total mass of chocolate needed for 140 bon-bons.

  total mass = mass per bon-bon * number of bon-bons

  total mass ≈ 1.826 g * 140

  total mass ≈ 255.64 g

4. Determine the cost of the chocolate by multiplying the total mass by the cost per gram.

  cost = total mass * cost per gram

  cost ≈ 255.64 g * $0.04/g

  cost ≈ $10.2256

5. Round the cost to the nearest cent.

  cost ≈ $10.23

Therefore, the chocolate for 140 bon-bons would cost approximately $6.13.

For more such questions on cost, click on:

https://brainly.com/question/2292799

#SPJ8

The number of cycles a sine function has in the interval from 0 to 2π, we need to look at the coefficient in front of the angle variable (in this case, ∅). In the function y = sin∅,

there is no coefficient, which means the coefficient is 1. For a sine function with a coefficient of 1, it completes one full cycle (i.e., goes through one complete period) in the interval from 0 to 2π. So, the number of cycles for this function in that interval is 1.

The amplitude of the sine function is the absolute value of the coefficient in front of the sine function. In this case, the coefficient is 1, so the amplitude is 1. The period of a sine function is given by the formula T = 2π/b, where b is the coefficient in front of the angle variable. For this function, since the coefficient is 1, the period is 2π. To summarize: The number of cycles for the function y = sin∅ in the interval from 0 to 2π is 1. The amplitude of the function is 1. The period of the function is 2π.

To know more about coefficient visit:

https://brainly.com/question/13431100

#SPJ11

The sine function y = sinθ has one cycle in the interval from 0 to 2π. The amplitude of the function is 1.The period of the function is 2π.

The sine function y = sinθ is a periodic function that repeats itself over a certain interval. In this case, we are looking at the interval from 0 to 2π.

To determine the number of cycles, we need to look at the range of values that θ takes within this interval. The sine function completes one full cycle as θ goes from 0 to 2π. Therefore, there is only one cycle in this interval.

The amplitude of the sine function is the maximum value it reaches, which is 1. The minimum value is -1. Therefore, the amplitude of y = sinθ is 1.

The period of the sine function is the distance it takes to complete one full cycle. In this case, the period is 2π. This means that the sine function repeats itself every 2π units.

Learn more about sine function:

https://brainly.com/question/32247762

#SPJ11