Albert was asked to list four decimals
between 0.25 and 0.50. What are four
decimals Albert may have written? Please help
Answers
Answer:
1. 0.35
2. 0.49
3. 0.36
Step-by-step explanation:
This works because just choose any number between 25 and 50 and add a 0. behind it.
Answer: 0.30 0.40 0.49 0.29
Step-by-step explanation:
all you need to do is list decimals that are above 0.25 and below 0.50
Related Questions
Audrey is a lifeguard and spots a drowning child 30 meters along the shore and 40 meters from the shore to the child. Audrey runs along the shore for a while and then jumps into the water and swims from there directly to the child. Audrey can run at a rate of 3 meters per second and swim at a rate of 1.2 meters per second. How far along the shore should Audrey run before jumping into the water in order to save the child
Answers
Audrey should run 30 meters along the shore before jumping into the water to save the child.
Let x be the distance Audrey should run before jumping into the water to save the child.
Find the time it takes Audrey to run to a point perpendicular to the child where she will jump into the water. Taking the perpendicular distance as y, then by Pythagoras' theorem, we have: y² = 40² - 30²y² = 1600 - 900y = √700y = 10√7 m
Audrey runs at 3 meters per second.
Hence, the time it takes her to cover the distance of y meters is:
t₁ = y/3 s
Find the time it takes Audrey to swim the remaining distance from the point she jumps into the water to the child.
The remaining distance is z where: z² = (30 - x)² + y²z² = 900 - 60x + x² + 700z² = x² - 60x + 1600z = √(x² - 60x + 1600 + 700)z = √(x² - 60x + 2300) m
Audrey swims at 1.2 meters per second.
Hence, the time it takes her to swim the distance of z meters is: t₂ = z/1.2 s
The total time it takes Audrey to save the child T = t₁ + t₂
T = y/3 + z/1.2s
Substituting the values for y and z above: T = 10√7/3 + √(x² - 60x + 2300)/1.2 s
Minimizing T
To minimize T, we differentiate T with respect to x and set the derivative equal to zero.
dT/dx = 0 - 20(x - 30)/(3√(x² - 60x + 2300)) = 0-20(x - 30)/(3√(x² - 60x + 2300)) = 0-20(x - 30) = 0x - 30 = 0x = 30 m
Therefore, Audrey should run 30 meters along the shore before jumping into the water to save the child.
To learn about distance here:
https://brainly.com/question/30395212
#SPJ11
The weekend Jerome earned 252. 50 in all. What was the dollar amount of the meals that Jerome served? Jerome served worth meals
Answers
The total amount of meals in dollars served by Jerome is equals to $1150.
Total amount Jerome earned this weekend = $252.50.
Jerome earned every weekend = $80.
Jerome earned cost of meals as tips by serving them = 15%
Let us consider the dollar amount of the meals that Jerome served 'x'.
Jerome earned a total of $252.50 for the weekend,
which consists of his earnings from the meals and his flat rate earnings.
Set up an equation to represent this,
x × 0.15 + 80 = 252.50
Simplifying this equation by subtracting 80 from both sides, we get,
⇒ 0.15x = 172.50
⇒ x = 1150
Therefore, the dollar amount of the meals that Jerome served was $1150.
Learn more about meals here
brainly.com/question/29705065
#SPJ4
The above question is incomplete, the complete question is:
The weekend Jerome earned 252. 50 in all. What was the dollar amount of the meals that Jerome served? Jerome served worth meals this weekend. Jerome earns 15%percent off all the costs of meal on all meals and he earns 80 dollars every weekend
The amunt of money that college students spend on rent each month is usually between $300 and $600. However, there are a few students who spend $1,300. What measure of spread would be most appropriate to measure the amount of money that college student spend on rent per month? Explain in detail why or why not one of the below measures would be used.
A. Median
B. Range
C. Standard Deviation
D. Inquartile Range
Answers
The range would be the most appropriate measure of spread in this case because it takes into account the extreme values of $300 and $1,300 and provides a clear measure of the difference between them.
To measure the amount of money college students spend on rent per month, the most appropriate measure of spread would be the range. The range is the simplest measure of spread and is calculated by subtracting the lowest value from the highest value in a data set. In this case, the range would be $1,300 - $300 = $1,000.
The median would not be the best choice in this scenario because it only represents the middle value in a data set. It does not take into account extreme values like the $1,300 rent expense.
Standard deviation would not be the most appropriate measure of spread in this case because it calculates the average deviation of each data point from the mean. However, it may not accurately represent the spread when extreme values like the $1,300 rent expense are present.
The interquartile range (IQR) would not be the best choice either because it measures the spread of the middle 50% of the data set. It does not consider extreme values and would not accurately represent the range of rent expenses in this scenario.
In summary, the range would be the most appropriate measure of spread in this case because it takes into account the extreme values of $300 and $1,300 and provides a clear measure of the difference between them.
Know more about Standard deviation here,
https://brainly.com/question/29115611
#SPJ11
Find the product of 32 and 46. Now reverse the digits and find the product of 23 and 64. The products are the same!
Does this happen with any pair of two-digit numbers? Find two other pairs of two-digit numbers that have this property.
Is there a way to tell (without doing the arithmetic) if a given pair of two-digit numbers will have this property?
Answers
Let's calculate the products and check if they indeed have the same value:
Product of 32 and 46:
32 * 46 = 1,472
Reverse the digits of 23 and 64:
23 * 64 = 1,472
As you mentioned, the products are the same. This phenomenon is not unique to this particular pair of numbers. In fact, it occurs with any pair of two-digit numbers whose digits, when reversed, are the same as the product of the original numbers.
To find two other pairs of two-digit numbers that have this property, we can explore a few examples:
Product of 13 and 62:
13 * 62 = 806
Reversed digits: 31 * 26 = 806
Product of 17 and 83:
17 * 83 = 1,411
Reversed digits: 71 * 38 = 1,411
As for determining if a given pair of two-digit numbers will have this property without actually performing the multiplication, there is a simple rule. For any pair of two-digit numbers (AB and CD), if the sum of A and D equals the sum of B and C, then the products of the original and reversed digits will be the same.
For example, let's consider the pair 25 and 79:
A = 2, B = 5, C = 7, D = 9
The sum of A and D is 2 + 9 = 11, and the sum of B and C is 5 + 7 = 12. Since the sums are not equal (11 ≠ 12), we can determine that the products of the original and reversed digits will not be the same for this pair.
Therefore, by checking the sums of the digits in the two-digit numbers, we can determine whether they will have the property of the products being the same when digits are reversed.
Which of the following is a
solution to the inequality below?
24 > -9 + 5x
X = 9
X = 12
X = 10
X = -12
Answers
After answering the provided question, we can conclude that Therefore, inequality the answer is X = 9.
What is inequality?In mathematics, an inequality is a non-equal relationship between two expressions or values. As a result, imbalance leads to inequality. In to mathematics, an inequality connects two values that are not equal. Inequality is not the same as equality. When two values are not equal, the not equal sign is commonly used (). Different inequalities, no matter how small or large, are used to contrast values. Many simple inequalities can be solved by modifying the 2 sides until only the variables remain. However, a number of factors contribute to inequality: Negative values are divided or added on both sides. Exchange left and right.
the inequality :
\(24 > -9 + 5x\\33 > 5x\\6.6 < x\\\)
So, the solution to the inequality is x > 6.6. Among the answer choices given, the only solution that satisfies this inequality is:
X = 9
Therefore, the answer is X = 9.
To know more about inequality visit:
https://brainly.com/question/29914203
#SPJ1
This work problem to solving Equations
Answers
Answer:
question por favor. ............ ....
Consider the reduction of the rectangle. A larger rectangle has a length of 18 inches and width of 8 inches. A smaller rectangle has a length of x inches and width of 3 inches. Write a proportion and then solve to find the missing measure of the reduced rectangle. What two ratios can be used in the proportion? What is the value of the missing measure?
Answers
Answer:
18/8 = x/3
x = 6.75 inches (length)
Step-by-step explanation:
Hi, to answer this question we have to write 2 ratios using the information given:
A larger rectangle has a length of 18 inches and width of 8 inches.
Inches /width = 18/8
So, for a rectangle that has a length of x inches and width of 3 inches the ratio is :
x/3
Solving for x:
18/8 = x/3
18/8 (3) =x
6.75 in= x
Feel free to ask for more if needed or if you did not understand something.
What is the equation of the line that passes through the point (5,-2) and has a slope of -2/5?
Answers
Answer:
y= -2/5x -2
Step-by-step explanation:
y = mx + b
jxjxjxjxnxjddjdjdjdjj
Vector v = RS has points R(-2, 11) and S(-14, 8). What are the magnitude and direction of RS? Round the answers to the thousandths place.

Answers
Answer: To find the magnitude and direction of vector RS, we first need to find the components of the vector, which are given by the differences in the x- and y-coordinates of R and S:
v = RS = <(-14) - (-2), 8 - 11> = <-12, -3>
The magnitude of v is given by the formula ||v|| = sqrt(a^2 + b^2), where a and b are the x- and y-components of v:
||v|| = sqrt((-12)^2 + (-3)^2) = sqrt(144 + 9) = sqrt(153) = 12.37
The direction of v is given by the angle that it makes with the positive x-axis, measured counterclockwise. We can find this angle using the formula theta = arctan(b/a), where a and b are the x- and y-components of v:
theta = arctan(-3/-12) = arctan(0.25) = -14.04 degrees (rounded to the nearest hundredth)
Therefore, the magnitude of RS is 12.37, and the direction of RS is 14.04 degrees below the negative x-axis.
Step-by-step explanation:
A solution that has a high concentration of hydrogen ions has what type of ph? responses 2 2 7 7 13 13 14
Answers
Answer:
2,
Step-by-step explanation:
It will be a low value < 7.
It.s in the acid range.t
Answer:
It would be 2!
I took the K-12 Quiz
Thats the question please help!! emergancy

Answers
Answer:
a) 1/25
b) 4/25
Step-by-step explanation:
What is the slope-intercept equation for the linear function represented by the
table?

Answers
Answer: y= 3/2x - 6
Step-by-step explanation:
The equation is y=mx + b
The y-intercept is when x = 0, so on the table y-intercept = -6
The slope is rise/run, we see that y increase by three and x increase by 2, so the slope is 3/2
to get the slope of any straight line, we simply need two points off of it, let's use those ones in the picture below.
\((\stackrel{x_1}{2}~,~\stackrel{y_1}{-3})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{3}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{3}-\stackrel{y1}{(-3)}}}{\underset{run} {\underset{x_2}{6}-\underset{x_1}{2}}} \implies \cfrac{3 +3}{4} \implies \cfrac{ 6 }{ 4 } \implies {\Large \begin{array}{llll} \cfrac{3 }{ 2 } \end{array}}\)
now, the y-intercept occurs when x = 0, recheck the picture below.

122. which of the following statements about influential scores are true? i. influential scores have large residuals. ii. removal of an influential score sharply affects the regression line. i. an x-value that is an outlier in the -variable is more indicative that a point is influential than a y-value that is an outlier the y-variable. (a) i and ii (b) 1 and iii (c) ii and iii (d) i, il, and ii (e) none of these are true
Answers
Influential scores, indicated by large residuals, have a significant impact on the regression line when removed from the data. These points, characterized by extreme x or y-values, can alter the slope and intercept of the regression line, emphasizing their importance in regression analysis.
The correct statements about influential scores are i and ii.
i. Influential scores have large residuals because they have a strong effect on the regression line. This means that if we remove an influential score from the data, it will significantly change the slope and intercept of the regression line.
ii. Removal of an influential score sharply affects the regression line because influential scores have a large impact on the regression line. If we remove an influential score, it will significantly change the slope and intercept of the regression line.
iii. This statement is not true. An x-value that is an outlier in the x-variable may be indicative of a point being influential, but a y-value that is an outlier in the y-variable can also be indicative of a point being influential.
Learn more about regression line here:
brainly.com/question/7656407
#SPJ11
Find the slope of a line perpendicular to the line whose equation is 6 � + � = 8 6x+y=8. Fully simplify your answer
Answers
Answer:
perpendicular slope = \(\frac{1}{6}\)
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
given
6x + y = 8 ( subtract 6x from both sides )
y = - 6x + 8 ← in slope- intercept form
with slope m = - 6
given a line with slope m then the slope of a line perpendicular to it is
\(m_{perpendicular}\) = - \(\frac{1}{m}\) = - \(\frac{1}{-6}\) = \(\frac{1}{6}\)
Will (-2)^2 and -2^2 have the same solution? Why or why not?
Answers
Answer:
No
Step-by-step explanation:
because (-2)^2 is 4 and -2^2 is -4
Help ASAP plz
Jacob bought 5 boxes of pencils for his drawing class. Each box contains 12 pencils. Which point on the graph shows the number of pencils he bought?

Answers
Answer:
it would be (5,60)
Step-by-step explanation:
he bought 5 boxes
each box has 12 pencils
5*12=60
If £2000 is placed into a bank account that pays 3% compound interest per year, how much will be in the account after 2 years?
Answers
Answer:
121.80
Step-by-step explanation:
I REALLY NEED THIS
Q.12
A student was asked to determine the y-intercept for the logarithmic function f (x) = log3(x + 2) + 1. Which of the following expressions would result in the correct y-intercept?
A. the quantity log 2 over log 3 end quantity plus 1
B. the quantity log 3 over log 2 end quantity plus 1
C. 3–1 – 2
D. (–1)3 – 2
Answers
f(0) = log3(0 + 2) + 1
f(0) = log3(2) + 1
Using the change of base formula, we can convert this expression to a common logarithm:
f(0) = log(2)/log(3) + 1
Therefore, the correct expression for the y-intercept is option A: the quantity log 2 over log 3 end quantity plus 1.
equation of the line that is parallel to x-3y=9 and passes through the point (-10,9)
Answers
keeping in mind that parallel lines have exactly the same slope, let's check for the slope of the equation above
\(x-3y=9\implies -3y=-x+9\implies y=\cfrac{-x+9}{-3} \\\\\\ y=\cfrac{-x}{-3}+\cfrac{9}{-3}\implies y=\cfrac{1}{3}x-3\qquad \impliedby \begin{array}{|c|ll} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}\)
so we're really looking for the equation of a likne whose slope is 1/3 and it passes through (-10 , 9)
\((\stackrel{x_1}{-10}~,~\stackrel{y_1}{9})\hspace{10em} \stackrel{slope}{m} ~=~ \cfrac{1}{3} \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{9}=\stackrel{m}{ \cfrac{1}{3}}(x-\stackrel{x_1}{(-10)}) \implies y -9= \cfrac{1}{3} (x +10) \\\\\\ y-9=\cfrac{1}{3}x+\cfrac{10}{3}\implies y=\cfrac{1}{3}x+\cfrac{10}{3}+9\implies {\Large \begin{array}{llll} y=\cfrac{1}{3}x+\cfrac{37}{3} \end{array}}\)
tell whether the lines for each pair of equations are parallel, perpendicular, or neither. Step-by-step solution please
y= -1/2x-11
16x-8y=-8
a. neither
b. perpendicular
c. parallel
Answers
They both have slope that are neither parallel nor perpendicular. Hence, the answer is (a) neither.
Given below are the pair of equations and we need to tell whether the lines for each pair of equations are parallel, perpendicular, or neither:
y= -1/2x-11 ...(1)
16x-8y=-8 ...(2)
We can convert both the equations into slope-intercept form i.e. y = mx + b. Then, we can compare the slope of both equations and determine their relationship.
(1) can be written as y = -1/2 x - 11
Comparing it with y = mx + b, we can say that the slope m = -1/2(2) can be written as:
16x - 8y = -8
=> 16x + 8 = 8y
=> y = 2x + 1
Comparing it with y = mx + b, we can say that the slope m = 2
Now, we can compare the slope of both the equations:
(1) has slope = -1/2 and
(2) has slope = 2
To determine the relationship between the two lines we will use the following criteria: If two lines have the same slope, they are parallel. If two lines have slopes that are negative reciprocals of each other, they are perpendicular. In all other cases, the lines are neither parallel nor perpendicular. The slope of (1) is -1/2 and slope of (2) is 2.
To learn more about slope, visit:
https://brainly.com/question/29184253
#SPJ11
An international organization must decide how to spend the $2,000,000 they have been allotted for famine relief in a remote area. They expect to divide the money between buying rice at $38.5/sack and beans at $35/sack. The number, P, of people who would be fed if they buy x sacks of rice and y sacks of beans is given by P= 1.1x + y - 108 What is the maximum number of people that can be fed, and how should the organization allocate its money?
Answers
To maximize the number of people that can be fed, subject to the constraint that the total cost of rice and beans cannot exceed $2,000,000. Let's first rewrite the cost constraint as an equation:
38.5x + 35y = 2,000,000
Now we can rewrite the expression for P in terms of one variable.
How optimal allocation for famine relief funds?
To find the maximum number of people that can be fed, which means we need to maximize the function P= 1.1x +y - 108 subject to the budget constraint:
38.5x + 35y = 2,000,000
First, we can rewrite the budget constraint as:
77x + 70y = 4,000,000y - 108.
To do this, we can use the constraints provided by the budget and the prices of rice and beans. Let's assume that the organization will spend all of the $2,000,000, so we have the equation:
38.5x + 35y = 2,000,000
This represents all the possible combinations of sacks of rice and beans that can be bought with the given budget.
To make the problem easier to work with, we can solve for y in terms of x:
y = (2,000,000 - 38.5x) / 35
Now we can substitute this expression for y into the function for P:
P = 1.1x + (2,000,000 - 38.5x) / 35 - 108
Simplifying this, we get:
P = (14x - 3250) / 35
To maximize P, we can take the derivative and set it equal to zero:
dP/dx = 14/35 = 0
Solving for x, we get:
x = 100,000/14
x = 7,142.857
Since we can't buy a fraction of a sack, we round down to the nearest whole number:
x = 7,142
Now we can use the equation we derived earlier to find the corresponding value of y:
y = (2,000,000 - 38.5 x) / 35
y = (2,000,000 - 38.5(7,142)) / 35
y = 22,000
Therefore, the maximum number of people that can be fed is:
P = 1.1 x + y - 108
P = 1.1(7,142) + 22,000 - 108
P = 30,346
So, the organization should buy 7,142 sacks of rice and 22,000 sacks of beans to feed the maximum number of people.
Learn more about constraint
brainly.com/question/13643976
#SPJ11
In this situation, what does the integer 0 represent?
Answers
Answer: first of all, please write out the problem.
Step-by-step explanation:
-8/9x +7/10=-119/30
solve pls
Answers
Answer:
x = 5.25
Step-by-step explanation:
subtract 7/10 from both sides of the equation
-8/9x +7/10 - 7/10 = -119/30-7/10
-8/9x = -119-21/30
-8/9x = -140/30
the negative signs cancels out and the right hand side reduced to the lowest tern
8/9x = 14/3
multiply both sides by the reciprocal of 8/9 which is 9/8
9/8 * 8/9x = 14/3 * 9/8
x = 21/4
x = 5.25
A family is going on a 603-mile car trip. So far they have driven 24% of the distance. Which is the best estimate for the number of miles they have driven so far?
Answers
Answer:
the best eatimated answer would be 150 miles.
24% of 603 = 144.72
so you can round it to 150
Answer:
24% of 603 is 144.72, so the best estimate would probably be 150 miles.
23. Kumar wishes to cut the biggest possible squares
from a rectangular sheet of paper without any
leftover paper. The sheet of paper has a length of
65 cm and a breadth of 50 cm.
(1) What is the length of each square?
(ii) How many squares can he cut altogether!
Answers
The length of each square Kumar cuts is 10cm and 13cm, and altogether he cuts 130 squares.
What is the length of squares cuts?The perimeter of a square is really the total length of all of its sides. As a result, we can calculate the perimeter of a square by adding its four sides. A square's sides are all equal. As a result, the perimeter of a square is calculated by multiplying the side of a square by four.Given that,
Length of paper = 65 cm
Breadth of paper = 50 cm
The length of each square,
The greatest common factor of 65 and 50 is 5.
So,
50/5 = 10
65/5 = 13
Therefore the length of each square is 10cm and 13cm.
To find the number of squares cut altogether ,
10 x 13 = 130 squares.
Therefore altogether Kumar cuts 130 squares.
To learn more about length of square refer to :
https://brainly.com/question/28353618
#SPJ1
what is h ( t ) = − t ( 16 t + 7 ) in standard form
PLEASE HELP !!!!
Answers
y = 2x - 4
y = 4x - 6
y = 3x - 4
that's what i got
Help
Will
Give
Brainlist
:-))) my

Answers
Ayan po thanks me laterr
Answer:
a
Step-by-step explanation:
1. 1 1/99 miles per hour
please answer it will help a lot!

Answers
The perimeter of the aqua rectangle is 72 feet. What is the measure of the rectangle’s longest side?
If you do not know the answer please don't plagiarize, post answers unrelated answers, or post incorrect answers.

Answers
Answer:
53
Step-by-step explanation:
72 = x + 3x - 4
72 = 4x - 4
72 + 4 = 4x - 4 + 4
76 = 4x
76/4 = 4x/4
x = 19
3(19) - 4 = 53
Hope this helps!
If you spend $50,000 on new furniture and it is depreciating about 20% per year, how much will it be worth by its third year?
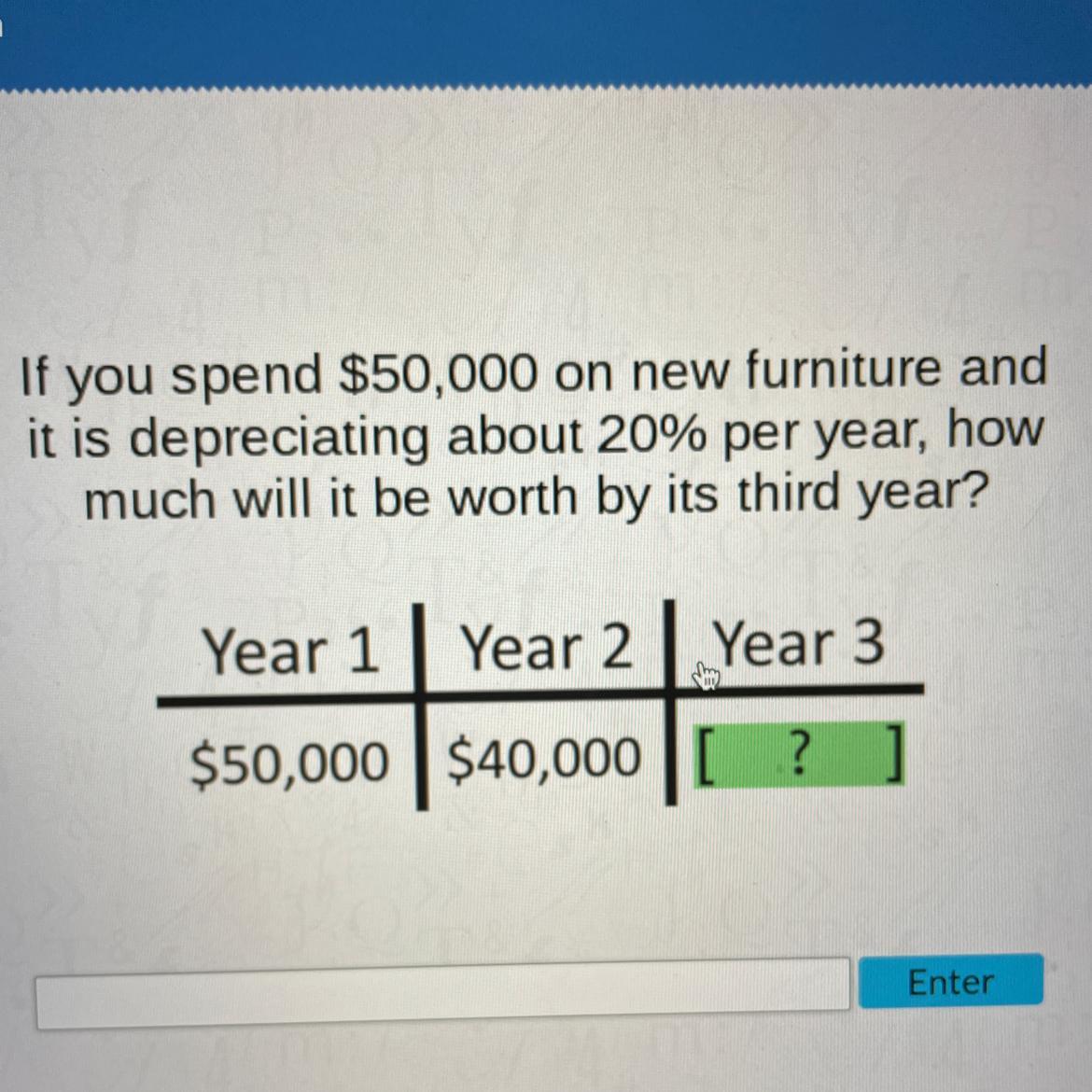
Answers
Answer:
$25,600
Step-by-step explanation:
Given: P = $50,000, r = 20% & t = 3 yearsFormula for depreciation is given as:\(A(t) = P\bigg(1-\frac{r}{100}\bigg)^t\)Plugging the values of P, r and t in the above formula, we find:\(A(3) = 50,000\bigg(1-\frac{20}{100}\bigg)^3\)\(\implies A(3) = 50,000\bigg(1-\frac{1}{5}\bigg)^3\)\(\implies A(3) = 50,000\bigg(\frac{4}{5}\bigg)^3\)\(\implies A(3) = 50,000\times\frac{64}{125}\)\(\implies A(3) =\$ 25,600\)So, after third year it will be worth by $25,600.