A room has a length of 5·25m and a width of 3·68m. What is the perimeter of the room?
Answers
Answer:
Perimeter = 17.86 m
Step-by-step explanation:
Perimeter = 2(L + W) = 2(5.25 + 3.68) = 17.86 m
Related Questions
The table represents a linear equation.
A two column table with 5 rows. The first column, x, has the entries, negative 10, negative 5, 10, 15. The second column, y, has the entries, 8, 7. 4, 3.
Which equation shows how (–10, 8) can be used to write the equation of this line in point-slope form?
y – 8 = –0.15(x – 10)
y + 8 = –0.15(x – 10)
y – 8 = –0.2(x + 10)
y + 8 = –0.2(x – 10)
Answers
Answer:
y – 8 = –0.2(x + 10)
Step-by-step explanation:
Edge 2020
Answer:
The Answer is option C y – 8 = –0.2(x + 10)
Step-by-step explanation:

given:x-5>-2. choose the solution set.
Answers
Answer:
\(x > 3\)
Step-by-step explanation:
\(x - 5 > - 2 \\ x > - 2 + 5 \\ x > 3\)
First you collect like terms
Then you add
Given m || n, find the value of x and y.
(9x-10)
(4x-5) (y-20)"
Answers
Given m || n, the calculaed values of x and y are x = 1 and y = 19
Finding the value of x and y.From the question, we have
Lines m and n are parallel
By the theorem of vertical angles, we have
9x - 10 = 4x - 5
When evaluated, we have
5x = 5
Divide by 5
So, we have
x = 1
By corresponsing angles, we have
4x - 5 = y - 20
So, we have
4(1) - 5 = y - 20
This gives
-1 = y - 20
So, we have
y = 19
Read mroe about angles at
https://brainly.com/question/28293784
#SPJ1
Two different cubes of the same size are to be painted, with the color of each face being chosen independently and at random to be either black or white. What is the probability that after they are painted, the cubes can be rotated to be identical in appearance
Answers
Answer:
Step-by-step explanation:
Define two ways of painting to be in the same class if one can be rotated to form the other.We can count the number of ways of painting for each specific class .
Case 1: Black-white color distribution is 0-6 (out of 6 total faces)
Trivially \(1^{2}\)=1 way to paint the cubes.
Case 2: Black-white color distribution is 1-5
Trivially all \(\frac{6}{5}\) =6 ways belong to the same class , so \(6^{2}\) ways to paint the cubes.
Case 3: Black-white color distribution is 2-4
There are two classes for this case: the class where the two red faces are touching and the other class where the two red faces are on opposite faces. There are 3 members of the latter class since there are 3 unordered pairs of 2 opposite faces of a cube. Thus, there are \(\frac{6}{4}\)-3=12 members of the former class . Thus, \(12^{2} + 3^{2}\) ways to paint the cubes for this case.
Case 4: Black-white color distribution is 3-3
By simple intuition, there are also two classes for this case, the class where the three red faces meet at a single vertex, and the other class where the three red faces are in a "straight line" along the edges of the cube. Note that since there are 8 vertices in a cube, there are 8 members of the former class and \(\frac{6}{3} -8=12\) members of the latter class. Thus, \(12^{2} - 8^{2}\) ways to paint the cubes for this case.
Note that by symmetry (since we are only switching the colors), the number of ways to paint the cubes for black-white color distributions 4-2, 5-1, and 6-0 is 2-4, 1-5, and 0-6 (respectively).
Thus, our total answer is\(\frac{2*(6^{2} + 1^{2}+ 12^{2}+ 3^{2})+12^{2}+8^{2}}{2^{12} } =\frac{588}{4096} = \frac{147}{1024}\)
What is the probability of getting 5 "sixes" in 7 rolls?
Answers
Answer:
The probability of getting a "six" on one roll of a fair six-sided die is 1/6.
To calculate the probability of getting 5 "sixes" in 7 rolls, we can use the binomial distribution formula, which is:
P(X = k) = (n choose k) * p^k * (1-p)^(n-k)
where:
P(X = k) is the probability of getting exactly k "successes" in n trials.
(n choose k) is the number of ways to choose k items from a set of n items.
p is the probability of "success" on any one trial.
(1-p) is the probability of "failure" on any one trial.
k is the number of "successes" we are interested in.
n is the total number of trials.
In this case, we want to find the probability of getting 5 "sixes" in 7 rolls, so:
n = 7 (the total number of rolls)
k = 5 (the number of "successes" we want to achieve)
p = 1/6 (the probability of getting a "six" on any one roll)
(1-p) = 5/6 (the probability of not getting a "six" on any one roll)
Using the binomial distribution formula, we can calculate:
P(X = 5) = (7 choose 5) * (1/6)^5 * (5/6)^2
= (7! / (5! * 2!)) * (1/6)^5 * (5/6)^2
= (21 * 1/7776 * 25/36)
= 0.0323
Therefore, the probability of getting exactly 5 "sixes" in 7 rolls of a fair six-sided die is approximately 0.0323, or about 3.23%.
Answer:
The probability of getting a "six" on one roll of a fair six-sided die is 1/6.
To calculate the probability of getting 5 "sixes" in 7 rolls, we can use the binomial distribution formula, which is:
P(X = k) = (n choose k) * p^k * (1-p)^(n-k)
where:
P(X = k) is the probability of getting exactly k "successes" in n trials.
(n choose k) is the number of ways to choose k items from a set of n items.
p is the probability of "success" on any one trial.
(1-p) is the probability of "failure" on any one trial.
k is the number of "successes" we are interested in.
n is the total number of trials.
In this case, we want to find the probability of getting 5 "sixes" in 7 rolls, so:
n = 7 (the total number of rolls)
k = 5 (the number of "successes" we want to achieve)
p = 1/6 (the probability of getting a "six" on any one roll)
(1-p) = 5/6 (the probability of not getting a "six" on any one roll)
Using the binomial distribution formula, we can calculate:
P(X = 5) = (7 choose 5) * (1/6)^5 * (5/6)^2
= (7! / (5! * 2!)) * (1/6)^5 * (5/6)^2
= (21 * 1/7776 * 25/36)
= 0.0323
Therefore, the probability of getting exactly 5 "sixes" in 7 rolls of a fair six-sided die is approximately 0.0323, or about 3.23%.
Select the number of solutions for each system of two linear equations.

Answers
Answer:
work is shown and pictured

C, infinitely many solutions.
B, one solution.
C, infinitely many solution.
A system of linear equations:A system of linear equations is a collection of one or more linear equations involving the same variables.
A system of linear equation has
one solution when the graph intersect at a point.no solution when the graphs are parallel.infinitely many solutions when the graphs are exact same line.According to the given questions
the given system of equations
(1). 2x+2y=3 and 4x+4y=6
if we see the graph of the above system of linear equations, the graphs are the" exact at same line".
Hence, they have infinitely many solution.
(2). 7x+5y=8 and 7x+7y =8
if we see the graph of the above system of linear equations, the graphs are intersecting at a single point.
Hence, there is only one solution.
(3). -2x+3y=7 and 2x-3y=-7
if we see the graph of the above system of linear equations, the graphs are exact at same line.
Hence, there is infinitely many solutions.
Learn more about the system of linear equations here:https://brainly.in/question/5130012
#SPJ2


Answer these please!!!

Answers
The graph of 3x-2y≤6 is the third graph, for 3x-2y<6 is the first graph, for 3x-2y>6 is the fourth graph and for 3x-2y≥6 is the second graph. The solution has been obtained using concept of linear inequality.
What is linear inequality?
A linear inequality is one that would produce a linear equation if the equals relation were used instead of the inequality. When multiplying or dividing both sides by a negative number in order to solve the inequality, the direction of the inequality is reversed. The entire set of solutions to an inequality is known as the solution set.
We are given for graphs, of which two graphs are dotted and two are simple straight line graphs.
The dotted graphs are drawn for the inequalities having < or >
Whereas the simple straight line graphs are drawn for the inequalities having ≤ or ≥.
Now, to notice the shaded pattern, we will see whether the equations are true for (0,0) or not
1. 3x-2y≤6
⇒ 0≤6
So, the equation is true for the point.
Hence, the third graph represents this equation.
2. 3x-2y<6
⇒ 0<6
So, the equation is true for the point.
Hence, the first graph represents this equation.
3. 3x-2y>6
⇒ 0>6
So, the equation is false for the point.
Hence, the fourth graph represents this equation.
4. 3x-2y≥6
⇒ 0≥6
So, the equation is false for the point.
Hence, the second graph represents this equation.
Hence, the graphs are matched with the inequalities.
Learn more about linear inequality from the given link
https://brainly.com/question/30340033
#SPJ1
Since, there are multiple questions so, the question answered above is attached below.

One winter night, the temperature outside was 10°F. Overnight, the temperature dropped to –2°F.
How many degrees did the temperature drop?
A)12
B)10
C)0
D)2
Answers
9514 1404 393
Answer:
A) 12
Step-by-step explanation:
The difference between 10 and -2 is ...
10 -(-2) = 10 +2 = 12
The temperature dropped 12 degrees F.
assessment started: unit 8 progress check: mcq part a. item 1 let f be the function given by f(x)=3xsinx. what is the average value of f on the closed interval 1≤x≤7 ?
Answers
To find the exact value, we would need to evaluate the definite integral, but it may not be practical to do so without further information or using numerical methods.
To find the average value of a function on a closed interval, you need to calculate the definite integral of the function over that interval and divide it by the length of the interval. In this case, we want to find the average value of the function f(x) = 3xsin(x) on the interval 1 ≤ x ≤ 7.
The average value of f on the interval [1, 7] is given by the formula:
Average value = (1/(b - a)) * ∫[a to b] f(x) dx
where a and b are the endpoints of the interval.
In our case, a = 1, b = 7, and f(x) = 3xsin(x). So, we can calculate the average value as follows:
Average value = (1/(7 - 1)) * ∫[1 to 7] (3xsin(x)) dx
Know more about integral here:
https://brainly.com/question/31059545
#SPJ11
If quadrilateral abcd is an isosceles trapezoid, which statements must be true? select three options bc ∥ ad bd ⊥ ac ba ≅ cd be ≅ ed ∠cba ≅ ∠bcd
Answers
The true statements among the given options are written below
bc || ad
ba ≅ cd
∠cba ≅ ∠bcd
In an isosceles trapezoid, there is one pair of legs of equal length and a pair of parallel lines.
Given that quadrilateral abcd is a isosceles trapezoid.
In the given trapezoid abcd
bc || ad ( pair of parallel sides )
So this is correct.
ba ≅ cd ( For an isosceles trapezoid legs are equal)
So this is correct
∠cba ≅ ∠bcd (According to the property of isosceles trapezoid )
So this is correct.
Hence, bc || ad, ba ≅ cd, ∠cba ≅ ∠bcd are correct
Learn more about quadrilaterals here https://brainly.com/question/14708246
#SPJ4
7 2 + 1 . 5 = 6 8 + 2
Answers
Answer:
I don't get it are you telling us a answer or is it a question?
Provide the algebraic model formulation for
each problem.
A farmer must decide how many cows and how many pigs to
purchase for fattening. He realizes a net profit of $40.00 on each
cow and $20.00 on
Answers
The farmer should buy x cows and y pigs so that the total cost of buying cows and pigs is less than or equal to M and the net profit is maximized.
The problem states that a farmer must determine the number of cows and pigs to purchase for fattening in order to earn maximum profit. The net profit per cow and pig are $40.00 and $20.00, respectively.
Let x be the number of cows to be purchased and y be the number of pigs to be purchased.
Therefore, the algebraic model formulation for the given problem is: z = 40x + 20y Where z represents the total net profit. The objective is to maximize z.
However, the farmer is constrained by the total amount of money available for investment in cows and pigs. Let M be the total amount of money available.
Also, let C and P be the costs per cow and pig, respectively. The constraints are: M ≤ Cx + PyOr Cx + Py ≥ M.
Thus, the complete algebraic model formulation for the given problem is: Maximize z = 40x + 20ySubject to: Cx + Py ≥ M
Therefore, the farmer should buy x cows and y pigs so that the total cost of buying cows and pigs is less than or equal to M and the net profit is maximized.
For more such questions on net profit
https://brainly.com/question/30403491
#SPJ8
What is 3times4 divided by6
Answers
Answer:
2
Step-by-step explanation:
3*4 Is 12 and 12 divided by 6 is 2 . You can also check your answer by multiplying 6 and 2 and that is twelve
A triangular prism is 36 millimeters long and has a triangular face with a base of 36 millimeters and a height of 24 millimeters. The other two sides of the triangle are each 30 millimeters. What is the surface area of the triangular prism?
Answers
The surface area of the triangular prism is
5752 square millimetersHow to find the surface area of the triangular prismThe surface area of the triangular prism is
= area of the two side rectangles + area of the base rectangles + area of the 2 triangles
= 2 * 36 * 30 + 36 * 36 + 2 * 1/2 * 36 * 24
= 2160 + 1296 + 1296
= 5752 square millimeters
Learn more about triangular prism at
https://brainly.com/question/29663752
#SPJ1
Which answer choice do I choose

Answers
Answer:
g = 2d - 8
g + d = 46
Step-by-step explanation:
It is given that the guitarist wrote eight less than twice as many songs as the drummer did, hence one would multiply by the number of songs the drummer wrote by two, and subtract eight.
It is also given that the combined total of songs that they both wrote is 46, hence one would add up the songs that they wrote, and attain a result fo 46.
Answer:
c
Step-by-step explanation:
Tim weighting this bc it said
In a survey, 200 college students were asked whether they live on campus and if they own a car. Their responses are summarized in the following table below.

Answers
If in a survey, 200 college students were asked whether they live on campus and if they own a car, 55% of college students in the survey don't own a car.
To find the percent of college students who don't own a car, we need to add up the number of students who don't own a car and divide it by the total number of students in the survey. In this case, the total number of students in the survey is 200.
From the table, we can see that there are 88 students who live on campus and don't own a car, and 22 students who don't live on campus and don't own a car. So the total number of students who don't own a car is 88 + 22 = 110.
To find the percentage, we divide the number of students who don't own a car by the total number of students in the survey and then multiply by 100 to get the percentage:
Percentage of students who don't own a car = (110/200) x 100% = 55%
When working with percentages, we need to divide the number we are interested in by the total and then multiply by 100 to get the percentage.
To learn more about survey click on,
https://brainly.com/question/26551559
#SPJ1
array indices must be positive integers or logical values matlabtruefalse
Answers
True; In MATLAB, array indices must be positive integers or logical values.
In MATLAB, array indices must indeed be positive integers or logical values. This means that when accessing elements within an array, the index values should be integers greater than zero or logical values (true or false). It is not permissible to use negative integers or non-integer values as array indices in MATLAB.
For example, consider an array called "myArray" with five elements. To access the first element of the array, you would use the index 1. Similarly, to access the fifth element, you would use the index 5. Attempting to use a negative index or a non-integer index will result in an error.
Using valid indices is crucial for proper array manipulation and accessing the correct elements. MATLAB arrays are 1-based, meaning the index counting starts from 1, unlike some programming languages that use 0-based indexing.
In MATLAB, array indices must be positive integers or logical values. This ensures proper referencing and manipulation of array elements. By adhering to this rule, you can effectively work with arrays in MATLAB and avoid errors related to invalid indices.
To know more about
In MATLAB, array indices start from 1. They are used to access specific elements within an array.
In MATLAB, array indices are used to access or refer to specific elements within an array. The index of an element represents its position within the array. It is important to note that array indices in MATLAB start from 1, unlike some other programming languages that start indexing from 0.
For example, consider an array A with 5 elements: A = [10, 20, 30, 40, 50]. To access the first element of the array, we use the index 1: A(1). This will return the value 10.
Similarly, to access the third element of the array, we use the index 3: A(3). This will return the value 30.
Array indices can also be logical values, which are either true or false. Logical indices are used to select specific elements from an array based on certain conditions. For example, if we have an array B = [1, 2, 3, 4, 5], we can use logical indexing to select all the elements greater than 3: B(B > 3). This will return the values 4 and 5.
Learn more:About MATLAB here:
https://brainly.com/question/30763780
#SPJ11
State three "real-world" variables X, Y, and Z for which you expect a marginal association between X and Y but conditional independence controlling for Z.
Answers
Three "real-world" variables for which you expect a marginal association between X and Y but conditional independence controlling for Z are:
- X = Hours spent studying
- Y = Grades in school
- Z = Intelligence
In this scenario, there is a marginal association between the hours spent studying (X) and the grades in school (Y), as it is expected that the more time a student spends studying, the better their grades will be.
However, when controlling for intelligence (Z), the association between X and Y becomes conditional independence, as intelligence can also affect grades in school.
In other words, the relationship between X and Y is no longer significant when controlling for Z.
For more such questions on Variables.
https://brainly.com/question/17344045#
#SPJ11
Sathish is going on a 210021002100-kilometer road trip with 222 friends, whom he will pick up 150150150 kilometers after he begins the trip and drop off when there are 150150150 kilometers remaining. the car consumes 666 liters of gas for every 100100100 kilometers, and gas costs \$1.20$1.20dollar sign, 1, point, 20 per liter.
Answers
Sathish will pay $64.8
When Satish is alone, kilometres:
Beginning at 150 kilometres and ending at 150 kilometres will be travelled 300 kilometres in total
When Satish is with friends, the total kilometres travelled is 2100 km:
And when Satish went alone he travelled 300 km
When Satish is with friends, total kilometres travelled: 2100-300 = 1800 km
Gas consumed in litres when Satish is alone: 100 kilometres use 6 litres of gas.
300 kilometres at 6 x 3 equals 18 litres.
So, when Satish is with friends, litres of gas are consumed: 100 kilometres use 6 litres of gas.
So, 6 × 18 for 1800 kilometres is equal to 108 litres.
Gas prices when Satish is on his own:
$1.2 per litre
18 x $1.2 = $21.6
Gas prices when Satish is travelling with friends
$1.2 per litre
108 x 1.2 = $129.6
Cost for each friend = $129.6/3 = $43.2
Satish will pay: Cost when travelling with friends + Cost when travelling alone
=$43.2+ $21.6
=$64.8
Learn more about arithmetic:
https://brainly.com/question/22260035
#SPJ4
pls help me out!! I'd appreciate it

Answers
Answer:
I believe it is C.
Step-by-step explanation:
What is the value of the following expression if x = 3 and y = 7.
y[x2−2(1+2)]÷y+52
Answers
Answer:
1+2=3
2*3=6
3*2=6
6-6=0
7*0=0
0/7=0
0+52=52
Answer: I believe it's 55.
Step-by-step explanation:
I replaced the letters with the numbers in the key, so it looked like this "7[3^(2)-2(1+2)]-:7+52" I really hope this helps but I'm not amazing. Goo luck! ^^
Convert 3.9m^2 into cm^2
I will leave good review!

Answers
Answer:
Step-by-step explanation:
To convert square meters to square centimeters, we need to multiply by the conversion factor (100 cm / 1 m)^2.
So,
3.9 m² = 3.9 × (100 cm / 1 m)²
3.9 m² = 3.9 × 10,000 cm²
3.9 m² = 39,000 cm²
Therefore, 3.9 square meters is equal to 39,000 square centimeters.
2 Find the value of each variable. 3 X= y = 60° y X
Answers
Answer:
20, 60
Step-by-step explanation:
3x=60
x=60/3
x=20
y=60
Answer:X=20 and Y=60
Step-by-step explanation: 3 x 20=60=60
select the function that does not have a well-defined inverse. group of answer choices f:→f(x)=⌈x 2⌉ f:→f(x)=−2x 5 f:→f(x)=⌈x⌉ f:→f(x)=3x 4
Answers
The inverse of the function f:→f(x)=⌈x⌉ is not well defined. Option 3 is the correct answer.
What is bijective?If a function f: A B meets both the injective (one-to-one function) and surjective (onto function) qualities, the function is said to be bijective or bijection. As a result, f(a) = b is true for every element "b" in the codomain B and precisely one element "a" in the domain A. The function is referred to as one-to-one communication if it meets this requirement.
In the given group of functions we observe that the function f:→f(x)=⌈x⌉ is not a one on one function.
That is, f(1) = ⌈1 - 1⌉ = 1
The function is not bijective.
Hence, the inverse of the function f:→f(x)=⌈x⌉ is not well defined. Option 3 is the correct answer.
Learn more about function here:
https://brainly.com/question/30721594
#SPJ1
Determine whether the equation represents an exponential function. Explain. Y= -3^x
Answers
The exponential function y = (- 3)ˣ is represent the exponential decay.
What is mean by Function?A relation between a set of inputs having one output each is called a function. and an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).
Given that;
The function is,
⇒ y = (- 3)ˣ
Now, We know that;
⇒ y = bˣ is an exponential function
if b > 1 it is growing
if b < 1 , then it is decreasing (decay).
Here, The function is,
⇒ y = (- 3)ˣ
By compare we get;
b = - 3 < 1
Hence, The exponential function y = (- 3)ˣ is represent the exponential decay.
Thus, The exponential function y = (- 3)ˣ is represent the exponential decay.
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ9
.1 Weather Forecast The temperature forecast for a city predicts the high for the day to be a normal random variable with expectation (mean) = 87.2, and standard deviation o = 6.4. What is the probability that the high will exceed 100?
Answers
The temperature forecast for a city predicts the high for the day to be a normal random variable with the mean = 87.2 and the standard deviation o = 6.4. We have to find the probability that the high will exceed 100.
The probability can be calculated as follows: \(P(X > 100) = P(Z > (100 - 87.2) / 6.4)P(Z > 2).\) The normal random variable is a continuous distribution that is symmetrical about the mean and bell-shaped with the mean in the center. The probability of the normal distribution beyond a specific point is calculated with the help of the standard normal distribution. Since the question asks us to find the probability of high temperature exceeding 100, we need to calculate the area under the standard normal curve to the right of 2.
This is because the standard normal distribution is a continuous probability distribution that has mean = 0 and standard deviation
o = 1 and is symmetric about the mean. Using the standard normal distribution table, the area to the right of 2 is approximately 0.0228. Hence, the probability that the high temperature will exceed 100 is 0.0228.
To know more about probability visit:-
https://brainly.com/question/29006544
#SPJ11
What is the product of 5/12 and 1/3
Answers
Answer:
5/6
Step-by-step explanation:
show that 3x4 1 is o(x4∕2) and x4∕2 is o(3x4 1).
Answers
3\(x^4\) + 1 is equivalent to \(x^{(4/2)}\) in terms of asymptotic growth rate. The value of 3\(x^4\) + 1 is O(\(x^{(4/2)}\)) and \(x^{(4/2)}\) is O(3\(x^4\) + 1).
To show that 3\(x^4\) + 1 is O(\(x^{(4/2)}\)), we need to find a constant C and a value of x such that:
|3\(x^4\) + 1| <= C|\(x^{(4/2)}\)|
For x >= 1, we can say that:
3\(x^4\) + 1 <= 4\(x^4\)
Taking the square root of both sides, we get:
sqrt(3\(x^4\) + 1) <= 2x²
Thus, we can choose C = 2 and x0 = 1, and we have:
|3\(x^4\) + 1| <= 2|\(x^{(4/2)}\)| for all x >= 1
Therefore, 3\(x^4\) + 1 is O(\(x^{(4/2)}\)).
To show that \(x^{(4/2)}\) is O(3\(x^4\) + 1), we need to find a constant C and a value of x such that:
|\(x^{(4/2)}\)| <= C|3\(x^4\) + 1|
For x >= 1, we can say that:
\(x^{(4/2)}\) <= x²
Thus, we can choose C = 1 and x0 = 1, and we have:
|\(x^{(4/2)}\)| <= |3\(x^4\) + 1| for all x >= 1
Therefore, \(x^{(4/2)}\) is O(3\(x^4\) + 1).
Since both 3\(x^4\) + 1 is O(\(x^{(4/2)}\)) and \(x^{(4/2)}\) is O(3\(x^4\) + 1).
Learn more about asymptotic growth at
https://brainly.com/question/28918543
#SPJ4
The piston stroke depend on * offset
crank angle
B crank radius the crank angle value when the piston at TDC is...... 120 30 0*2pi B the maximum ratio of crank radius to connected length is *
4
0.25-0.3 0.25 0.3
Answers
The crank angle value when the piston is at Top Dead Center (TDC) is 0 radians or 0 degrees. The maximum ratio of the crank radius to the connected length is 0.3.
The crank angle value refers to the angle between the crankshaft and a reference point when measuring the position of the piston. When the piston is at Top Dead Center (TDC), it is at its highest point in the cylinder. The crankshaft is positioned such that the connecting rod is aligned with the crank radius and the piston is at the topmost position. This corresponds to a crank angle value of 0 radians or 0 degrees.
Regarding the maximum ratio of the crank radius to the connected length, this value is given as 0.3. The crank radius is the distance from the center of the crankshaft to the center of the crank pin, and the connected length is the distance from the center of the crank pin to the center of the piston pin. The maximum ratio of 0.3 indicates that the crank radius is 0.3 times the connected length.
It's important to note that these values are specific to the context of the problem statement provided. Different engines or mechanisms may have different values for the crank angle at TDC and the maximum ratio of crank radius to connected length.
Learn more about crank angle value here:
https://brainly.com/question/32140084
#SPJ11
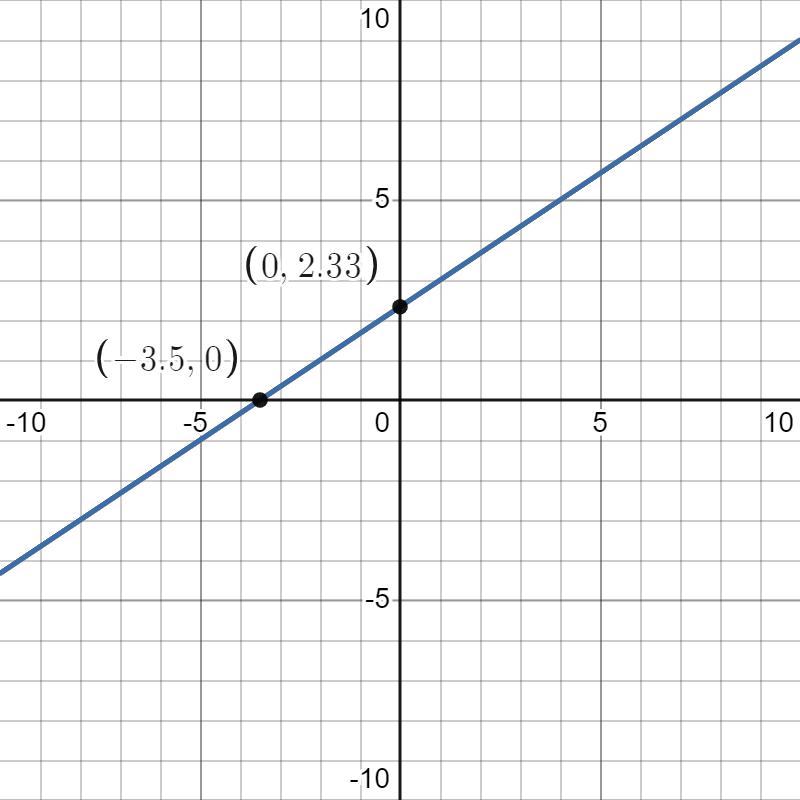
What inequality is graphed below?
