A person invested \$8,700$8,700 in an account growing at a rate allowing the money to double every 15 years. How long, to the nearest tenth of a year would it take for the value of the account to reach \$23,100$23,100?
Answers
Answer:21.13208319 =21.1
Answer: Probly 10 years or less
Step-by-step explanation:
Related Questions
At noon, ship A is 10 nautical miles due west of ship B. Ship A is sailing west at 16 knots and ship B is sailing north at 21 knots. How fast (in knots) is the distance between the ships changing at 4 PM? (Note: 1 knot is a speed of 1 nautical mile per hour.)
Answers
At \($5 \mathrm{pm}$\) the distance between the ships is changing at the speed of \($\mathbf{3 0 . 2 1}$\) knots
Firstly we need to an equation to represent both ships and the distance between each. A is moving \($25 \mathrm{knots}$\) west and \($B$\) is moving \($17 \mathrm{knot}$\) north. \($D$\)will be the distance between the two. Drawing it, you'll notice that it creates a right triangle.
So we use the Pythagorean Theorem:
\($$D^{\wedge} 2=A^{\wedge} 2+B^{\wedge} 2$$\)
Differentiate in relation to time:
\($$2 \mathrm{D}(\mathrm{dD} / \mathrm{dt})=2 \mathrm{~A}(\mathrm{dA} / \mathrm{dt})+2 \mathrm{~B}(\mathrm{~dB} / \mathrm{dt})$$\)
Now we must find all of our variables.
\(& A=\text { time(speed })+\text { original distance }=5(25)+10=135 \\\)
\(& B=5(17)+0=85 \\\)
\(& D=V\left(A^{\wedge} 2+B^{\wedge} 2\right)=159.53 \\\)
\(& d A / d t=25 \\\)
\(& d B / d t=17\)
Plug in all your variables and solve for
\($(\mathrm{dD} / \mathrm{dt})$ :\)
\(& 2 \mathrm{D}(\mathrm{dD} / \mathrm{dt})=2 \mathrm{~A}(\mathrm{dA} / \mathrm{dt})+2 \mathrm{~B}(\mathrm{~dB} / \mathrm{dt}) \\\)
\(& 2(159.53)(\mathrm{dD} / \mathrm{dt})=2(135)(25)+2(85)(17) \\\)
\(& 319.061(\mathrm{dD} / \mathrm{dt})=9640 \\\)
\(& \mathrm{dD} / \mathrm{dt}=9640 / 319.061 \\\)
\(& \mathrm{dD} / \mathrm{dt}=30.21 \text { knots }\end{aligned}\)
At \($5 \mathrm{pm}$\) the distance between the ships is changing at the speed of \($\mathbf{3 0 . 2 1}$\) knots
To know more about Pythagoras Theorem
https://brainly.com/question/343682
#SPJ4
Help I am very confused
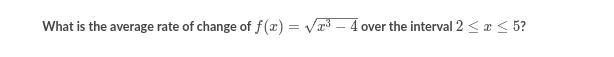
Answers
The function f(x) has an average rate of 3 over the interval 2 ≤ x ≤ 5
How to determine the average rate of change f?The interval is given as
2 ≤ x ≤ 5
This can be rewritten as
x = 2 to x = 5
This can also be represented as
(a, b) = [2, 5]
The function is given as
f(x) = √x³ - 4
Calculate f(2) and f(5)
So, we have
f(2) = √2³ - 4 = 2
f(5) = √5³ - 4 = 11
The average rate of change of the function is then calculated as
Rate = [f(b) - f(a)]/[b - a]
This gives
Rate = [f(5) - f(2)]/[5 - 2]
So, we have
Rate = [11 - 2]/[5 - 2]
Evaluate
Rate = 3
Hence, the average rate of change f is 3
Read more about average rate of change at
brainly.com/question/8728504
#SPJ1
4. Uncle Royce is 42. What is his target heart rate range?
O 120-180 beats per minute
O 150-200 beats per minute
O116-160 beats per minute
O170-236 beats per minute
Answers
Step-by-step explanation:
70 to 85 % of his maximum
Maximum is estimated to be 220 - age = 220 - 42 = 178
70% of this is 125
85 % is 89 151
I believe I would go with the third choice 116-160 bpm
Extrema interpreting functions
Answers
Answer:
In mathematics, the extrema of a function refer to the maximum and minimum values that the function can take on. These values can be local extrema, which occur within a certain range of the function, or global extrema, which are the maximum and minimum values over the entire domain of the function.
To find the extrema of a function, one can use a variety of techniques, such as taking the derivative of the function and setting it equal to zero to find the points of stationary values, or using the second derivative test to determine whether a stationary point is a local maximum or minimum.
Interpreting the extrema of a function can provide valuable information about the behavior of the function. For example, the global maximum of a function might represent the highest possible value that the function can attain, while the global minimum might represent the lowest possible value. Local extrema can also be important, as they can indicate changes in the slope or concavity of the function, which can have important implications for applications such as optimization or modeling real-world phenomena.
To prepare for the winter season the manager of an outdoor ice skating rink ordered 4,920 pounds of sand to keep around the skating rink from being yo slippery One bag of sand is 40 which equation can be used to find the number of bag of sand ,b, the manager order
Answers
Answer:
hope this helps UwU
Step-by-step explanation:

The required equation represents the number of bags of sand is b = 4920 ÷ 40.
What is the equation?The equation is the relationship between variables and represented as y = ax + b is an example of a polynomial equation.
here,
To prepare for the winter season the manager of an outdoor ice skating rink ordered 4,920 pounds of sand to keep around the skating rink from being yo slippery One bag of sand is 40 points.
Let the number of bags be b,
40 × = 4920
b = 4920 ÷ 40
Thus, the required equation that represents the number of bags of sand is b = 4920 ÷ 40.
Learn more about equations here:
brainly.com/question/10413253
#SPJ2
NO LINKS!! URGENT HELP PLEASE!!!
Please help me with Growth rate and Initial Value only

Answers
Answer:
growth rate: 4
y-value: 19
equation: y=4x+19
Step-by-step explanation:
Growth Rate:
The growth rate of a linear function is constant. This means that the function will increase or decrease by the same amount for every unit increase in x.
This can be found by dividing the change in y-values by the change in x-values.
For the question:
The change in y-values is 11-7=4,
and the change in x-values is +1.
Therefore, the growth rate is 4.
\(\hrulefill\)
Initial Value: The initial value of a linear function is the value of the function when x is 0.
In this case, the initial value is 19.
This can be found by looking at the y-value of the point where x is 0.
In this case, the y-value is 19.
\(\hrulefill\)Equation: The equation of a linear function is y = mx + b, where m is the slope and b is the y-intercept.
Using the table you provided, we can find the slope by using two points on the line.
Let’s use (-3, 7) and (1, 23).
The slope is (y2-y1)/(x2-x1)=(23-7)(1-(-3)=16/4=4
Now,
Taking 1 point (-3,7) and slope 4.
we can find the equation by using formula:
y-y1=m(x-x1)
y-7=4(x+3)
y=4x+12+7
y=4x+19
Therefore, the equation of the given table is y=4x+19\(\hrulefill\)
Answer:
Growth rate: 4
Initial value: 19
Equation: y = 4x + 19
Step-by-step explanation:
The slope of a linear function represents its growth rate.
Therefore, the growth rate of a linear function can be found using the slope formula.
Substitute two (x, y) points from the table into the slope formula, and solve for m. Substituting points (0, 19) and (1, 23):
\(\textsf{slope}\:(m)=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{23-19}{1-0}=\dfrac{4}{1}=4\)
Therefore, the growth rate of the linear function is 4.
The initial value of a linear function refers to the y-intercept, which is the value of the y when x = 0.
From inspection of the given table, y = 19 when x = 0.
Therefore, the initial value of the linear function is 19.
To write a linear equation given the growth rate (slope) and initial value (y-intercept), we can use the slope-intercept formula, which is y = mx + b. The slope is represented by the variable m, and the y-intercept is represented by the variable b.
As the growth rate of the given linear function is 4, and the initial value is 19, substitute m = 4 and b = 19 into the slope-intercept formula to create the equation of the linear function represented by the given table:
\(\boxed{y=4x+19}\)
Convert: 120 quartsgallons
Answers
EXPLANATION
The relationship between quarts and gallons is as follows:
\(1\text{ gallon=4 quarts}\)Therefore, we can apply the unit method in order to get the number of gallons:
\(Number\text{ of gallons=120 quarts*}\frac{1\text{ gallon}}{4\text{ quarts}}\)Simplifying:
\(Number\text{ of gallons=30 gallons}\)In conclusion, the solution is 30 gallons.
Liam will spin the pointer one time. What is the probability that the pointer will land on red?
Answers
Answer:
Step-by-step explanation:
What are the other colors?
if there are two colors ( red and another color ) then the probability of the pointer landing on red will be 1/2
similarly if there are 3 colors ( red and two other colors) then the probability of the pointer landing on red will be 1/3 ....
depends on how many colors are there
a study of long-distance phone calls made from general electric reveled the length of the calls, in minutes, follows the normal probability distribution. the mean length of time per call was 4.5 minutes and the standard deviation was 0.70 minutes. what is the probability that calls last between 4.0 and 6.0 minutes?
Answers
The probability that calls last between 4.0 and 4.6 minutes will be around 0.4332.
we have to standardize the values and utilize the standard typical dispersion table or calculator.
To discover the z-scores for 4.0 and 6.0 minutes:
z1 = (4.0 - 6.0 ) / 0.70 = 2.8
z2 = (4.5 - 6.0 ) / 0.70= 2.1
Since Employing a standard ordinary conveyance table, we are able to discover the likelihood of the calls enduring between 4.0 and 4.6 minutes:
P(0 ≤ Z ≤ 2.1) = 0.4332
However the likelihood that calls final between 4.0 and 4.6 minutes is 0.4332, or around 0.4332.
To know more about probability refer to this :
brainly.com/question/24756209
#SPJ1
find the domain of:
this

Answers
Answer:
The domain of a function is the set of all real numbers for which the function is defined. In this case, the function is defined when the denominator is not equal to zero. The denominator is equal to zero when x=1. Therefore, the domain of the function is all real numbers except for x=1.
In interval notation, the domain is written as
(-∞,1) ∪ (1,∞)
Step-by-step explanation:
What is the multiplicative rate of change for the exponential function f(x)=2(5/2)^-x
Answers
The multiplicative rate of change for the exponential function is
5/2How to find the multiplicative inverseThe multiplicative rate of change for an exponential function is determined by the base of the exponent.
In this case, the function is f(x) = 2(5/2)⁻ˣ,
where the base of the exponent is (5/2).
The multiplicative rate of change for an exponential function with a base greater than 1 is greater than 1, indicating exponential growth. Conversely, if the base is between 0 and 1, the multiplicative rate of change is less than 1, representing exponential decay.
In this function, the base (5/2) is greater than 1.
Learn more about exponential function at
https://brainly.com/question/2456547
#SPJ1
-4(y - 2) = 12
y = ?
Answers
Answer:
Hello! answer: -1
Hope that helps!
-4 3/5÷1 1/5
Answer in simplest form
Answers
Answer: -23/6
Step-by-step explanation:
In the Republic of Yemen, real per capita gross domestic product (GDP) in 2004 was $709.97. By 2005, it had increased to $832.84. At what rate did Yemen's economy grow in that time?
Answers
Answer:
$122.87 or 17.31% per year.
Step-by-step explanation:
Rate of growth
It's a measure of how a magnitude increases in a determined time. If the magnitude changes from x1 to x2 in a time t, then the rate of growth is:
\(\displaystyle r=\frac{x2-x1}{t}\)
The GDP of Yemen went from $709.97 to $832.84 in one year. Thus:
\(\displaystyle r=\frac{832.84-709.97}{1}\)
r=$122.87 per year
It can also be expressed as a percentage with respect to the initial value:
\(\displaystyle r=\frac{122.87}{709.97}*100\%\)
r=17.31% yearly
Answer:
$122.87 or 17.31% per year.
Step-by-step explanation:
Rate of growth
It's a measure of how a magnitude increases in a determined time. If the magnitude changes from x1 to x2 in a time t, then the rate of growth is:
The GDP of Yemen went from $709.97 to $832.84 in one year. Thus:
r=$122.87 per year
It can also be expressed as a percentage with respect to the initial value:
r=17.31% yearly
Can somebody help me i have to drag the functions on top onto the bottom ones to match their inverse functions.

Answers
Answer:
1. x/5
2. cubed root of 2x
3.x-10
4.(2x/3)-17
Step-by-step explanation:
Answer:
Step-by-step explanation:
1. Lets find the inverse function for function f(x)=2*x/3-17
To do that first express x through f(x):
2*x/3= f(x)+17
2*x=(f(x)+17)*3
x=(f(x)+17)*3/2 done !!! (1)
Next : to get the inverse function from (1) substitute x by f'(x) and f(x) by x.
So the required function is f'(x)=(x+17)*3/2 or f'(x)=3*(x+17)/2
This is function is No4 in our list. So f(x)=2*x/3-17 should be moved to the box No4 ( on the bottom) of the list.
2. Lets find the inverse function for function f(x)=x-10
To do that first express x through f(x):
x= f(x)+10
x=f(x)+10 done !!! (2)
Next : to get the inverse function from (2) substitute x by f'(x) and f(x) by x.
So the required function is f'(x)=x+10
This is function is No3 in our list. So f(x)=x-10 should be moved to the box No3 ( from the top) of the list.
3.Lets find the inverse function for function f(x)=sqrt 3 (2x)
To do that first express x through f(x):
2*x= f(x)^3
x=f(x)^3/2 done !!! (3)
Next : to get the inverse function from (3) substitute x by f'(x) and f(x) by x.
So the required function is f'(x)=x^3/2
This is function No2 in our list. So f(x)=sqrt 3 (2x) should be moved to the box No2 ( from the top) of the list.
4.Lets find the inverse function for function f(x)=x/5
To do that first express x through f(x):
x=f(x)*5 done !!! (4)
Next : to get the inverse function from (4) substitute x by f'(x) and f(x) by x.
So the required function is f'(x)=x*5 or f'(x)=5*x
This is function No1 in our list. So f(x)=x/5 should be moved to the box No1 ( on the top) of the list.
Which expression represents the volume of a shipping box? s(2^3) (8 + 2)3 (8x2)3 8+23
Answers
As a result, the right response is s(23), which can be written as \(8s^3\) as to calculate a shipping box's volume is based on the box's dimensions.
what is volume ?A tri object's volume is a measurement of how much space it takes up. The usual measurement tool is a cubic unit, such as a cubic metre (m3) or cubic foot (ft3). The formula used to determine a solid item's volume depends on the shape of the object. For instance, the volume of a cube is determined by multiplying the length of a single of its sides by six, whereas the capacity of a cylinder is determined by dividing the area of its base by the diameter. Engineering, mathematics, and architecture are just a few of the disciplines where the idea of volume is crucial.
given
The formula used to calculate a shipping box's volume is based on the box's dimensions.
The box's volume can be expressed as follows if its side length is s:
\(V = s^3\)
As a result, the right response is s(23), which can be written as \(8s^3\) as to calculate a shipping box's volume is based on the box's dimensions.
To know more about volume visit :-
https://brainly.com/question/1578538
#SPJ1
Two fractions between 2 and 2 1/2
Answers
Answer:
2 2/5 and 2 2/100
Step-by-step explanation:
The answers range in many ways! Whatever floats your boat to pick!
Hope this helped! :)
Help me out? Please! Thank you!

Answers
Answer:
A
Step-by-step explanation:
pls give brainliest
The table shows three unique functions.
x f(x) g(x) h(x)
-2
4
6
-3
-1
1
2
1
4-
2
1
1
55 752
6
8
1
Hit
6:
Mark this and return
-25
Which statements can be used to compare the
characteristics of the functions? Select two options.
Of(x) has an all negative domain.
g(x) has the greatest maximum value.
All three functions share the same range.
Oh(x) has a range of all negative numbers.
All three functions share the same domain.
Answers
Answer:
The statements that can be used to compare the characteristics of the functions are:
1. g(x) has the greatest maximum value.
2. All three functions share the same domain.
Explanation:
- The table shows the values of three functions - f(x), g(x), and h(x) - evaluated at different values of x.
- We cannot determine the domain of f(x) or h(x) from the given table but we can see that g(x) has a domain of all real numbers.
- We can see that g(x) has the highest maximum value among the three functions, which is 8.
- We cannot determine the range of f(x) or g(x) from the given table but we can see that h(x) has a range of all negative numbers.
- We cannot say anything about the domain or range of f(x) based on the given table.
- Therefore, the two statements that can be used to compare the characteristics of the functions are: g(x) has the greatest maximum value and all three functions share the same domain.
Write the equation of the ellipse with a minor axis length of 8 units and foci at (-7, 4) and (7, 4).
Answers
Given:
Minor axis length is 8 units.
Focci of elipse : (-7,4) and (7,4).
Required:
To find the equation of the elipse.
Explanation:
The general equation of elipse is
\(\begin{gathered} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \\ a>b \end{gathered}\)It is given that minor axis length is 8 units.
Therefore the value of b becomes 4.
Now we have to find the value of a.
And given that the focci points are (-7,4) and (7,4).
Here consider
\(c=7\)Now,
\(\begin{gathered} c^2=a^2-b^2 \\ 7^2=a^2-4^2 \\ 49=a^2-16 \\ 49+16=a^2 \\ a^2=65 \\ a=\sqrt{65} \end{gathered}\)Therefore, the equation of the elipse becomes
\(\frac{x^2}{65}+\frac{(y-4)^2}{16}=1\)Final Answer:
\(\frac{x^{2}}{65}+\frac{(y-4)^2}{16}=1\)Answer:
Step-by-step explanation:
x^2/65+(y-4)^2/16=1
Kenny reads 5/8 pages of his book in 2/3 minutes. How many pages will Kenny read in one minute answer as fraction
Answers
Answer:
15/16
Step-by-step explanation:
The unit rate is pages per minute, so divide the pages by the minutes:
(5/8)/(2/3) = (5/8)·(3/2) = 15/16 pages per minute
Bryan invests $6500 in two different accounts. The first account paid 11 %, the second account paid 7 % in interest. At the end of the first year he had earned $519 in interest. How much was in each account?
$ at 11 %
$ at 7 %
Answers
Bryan invested $1600 in the first account (earning 11% interest) and $4900 (6500 - 1600) in the second account (earning 7% interest).
Let's assume that Bryan invested an amount of x dollars in the first account, which earns 11% interest, and (6500 - x) dollars in the second account, which earns 7% interest.
The interest earned from the first account can be calculated as 0.11x, and the interest earned from the second account can be calculated as 0.07(6500 - x).
According to the problem, the total interest earned after one year is $519. So we can set up the equation:
0.11x + 0.07(6500 - x) = 519
Simplifying the equation:
0.11x + 455 - 0.07x = 519
0.04x + 455 = 519
0.04x = 64
x = 64 / 0.04
x = 1600
Therefore, Bryan invested $1600 in the first account (earning 11% interest) and $4900 (6500 - 1600) in the second account (earning 7% interest).
for such more question on Bryan invested
https://brainly.com/question/20690803
#SPJ8
HELP PLEASE WILL GIVE BRAINLIEST!

Answers
Answer:
So easy
Step-by-step explanation
on the y axis put -5 and then for x axis put -6
Answer:
(2,0) and (4,0)
Step-by-step explanation:
The roots are the values of x for which y = 0, or where the graph crosses the x-axis. (2,0) and (4,0)
A local Chinese restaurant sells combination meals for $9.50 a piece. If the cost of an order is proportional to the number of meals ordered, how much is the delivery charge?
Answers
Answer:
Step-by-step explanation:
bghgytythghgf66ef
Suppose a normally distributed set of data with 4800 observations has a mean of 195 and a standard deviation of 12. Use the 68-95-99.7 Rule to determine the number of observations in the data set expected to be below a value of 231. Round your result to the nearest single observation.
Answers
Answer:
The number of observations in the data set expected to be below a value of 231 is of 4793.
Step-by-step explanation:
The Empirical Rule states that, for a normally distributed random variable:
68% of the measures are within 1 standard deviation of the mean.
95% of the measures are within 2 standard deviation of the mean.
99.7% of the measures are within 3 standard deviations of the mean.
In this problem, we have that:
Mean = 195
Standard deviation = 12
The normal distribution is symmetric, which means that 50% of the observations are above the mean and 50% are below.
Proportion of observations below 231:
231 = 195 + 3*12
So 231 is three standard deviations above the mean.
Of the 50% of observations below the mean, all are below 231.
Of the 50% of observations above the mean, 99.7% are between the mean of 195 and three standard deviations above the mean(231).
So, the proportion of observations below 231 is:
\(P = 0.5*1 + 0.5*0.997 = 0.9985\)
Out of 4800:
0.9985*4800 = 4793
The number of observations in the data set expected to be below a value of 231 is of 4793.
Tracy bought a new flat-screen television. One side of the television screen is 49 inches and the other side is 27 inches. What is the length of the diagonal of the television screen? Answer choices are rounded to the nearest inch.
Answers
Answer:
56 inches (rounded)
Step-by-step explanation:
to solve this problem use the pythagreon theorem (a^2 + b^2 = c^2)
a and b represent the measurements of the side lengths of the TV in this case
plug in 27 for a and 49 for b
27^2 + 49^2 = c^2
2401 + 729 = c^2
c = 55.946 or 56
56 inches (rounded) is the length of the diagonal of the television screen.
What is Pythagorean theory?The Pythagorean theorem states, "In a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides."The sides of this triangle were called the perpendicular, the base and the hypotenuse.This theorem is a very useful tool and forms the basis of more complex trigonometry, such as the Pythagorean inverse theorem.Euclid provided two very different proofs for the Pythagorean theorem.Euclid was the first to mention and prove his Theorem 47 in his Book I, also known as I 47 or Euclid I 47. This is perhaps the most famous of all the proofs of the Pythagorean theorem.The Pythagorean Theorem is named after Pythagoras of Samos, a religious leader and mathematician who believed that everything in the universe was made up of numbers.56 inches (rounded) is the length of the diagonal of the television screen.
to solve this problem use the pythagreon theorem (a^2 + b^2 = c^2)
a and b represent the measurements of the side lengths of the TV in this case
plug in 27 for a and 49 for b
27^2 + 49^2 = c^2
2401 + 729 = c^2
c = 55.946 or 56
To learn more about Pythagorean theorem, refer
brainly.com/question/343682
#SPJ2
what is the actual number of kilometers that is represented by 5 centimeters on the map
Answers
Find the areas of the figures below. Can you find more than one method for each shape?
Please explain how you solved this. I am struggling.

Answers
Using area formula,
a. Area of the trapezium = 47.5m².
b. Area of parallelogram = 54inches².
Define area?The area of a thing is the amount of space it occupies in two dimensions. It is a way to count how many unit squares completely round the surface of a closed figure. The standard unit of area is the square unit, which is usually expressed as square inches, square feet, etc.
a. Sides of the trapezium are, a = 5m and b = 14m.
Height, h = 5m.
Area of the trapezium = (a+b)/2 × h
= (5 + 14)/2 × 5
= (19× 5)/2
= 95/2
= 47.5m².
b. Height of parallelogram = 6inches.
Base of parallelogram = 9inches.
Area = b × h
= 6 × 9
= 54inches².
To know more about area, visit:
https://brainly.com/question/27683633
#SPJ1
If |–4 + x| = 8, x could equal which of the following?
Answers
Answer:
x^1= -4, x^2= 12
Step-by-step explanation:
Find the sum of the arithmetic sequence 5, -2, -9, -16..., -44
Answers
Answer:
-136.5
Sn=A1+An/2*n
Step-by-step explanati
d=-2-5=-7
A1=5 An=-44 n=-49/7=7
S7=5+(-44)/2*7=19.5*7=-136.5