A car travels 500 meters the first minute. Each minute after,the car travels 160meters .if this pattern continues ,what is the distance the car travels in 15 minutes?
An=a1+d(n-1)
A. 2740
B. 2900
C. 7660
D. 7160

Answers
Answer:
a?
Step-by-step explanation:
Related Questions
Nadia was asked to show that the sine of an angle and the cosine of its complement are equal. To do this, she drew the diagram below and found sin(57°) and cos(33°)
Which expression below represents both sin(57°) and cos(33°)?

Answers
Answer:
c
Step-by-step explanation:
c
the expression that represents both sin(57°) and cos(33°) is 15/x
To determine the expression that represents both sin(57°) and cos(33°), we need to use the given information about the triangle.
Let's label the angle opposite the perpendicular side as angle A and the angle opposite the base as angle B.
Since the perpendicular is 15 and the base is 17, we can use the Pythagorean theorem to find the length of the hypotenuse (x):
x² = 15² + 17²
x² = 225 + 289
x² = 514
x = √514
Now, let's analyze the angles. The angle A (opposite the perpendicular) is 33°, while the angle B (opposite the base) is 57°.
Therefore, sin(57°) is represented by 15/x, and cos(33°) is represented by 15/x.
Thus, the expression that represents both sin(57°) and cos(33°) is 15/x
Learn more about Pythagorean theorem here
https://brainly.com/question/28361847
#SPJ6
recall the notion of average value from one-variable calculus: if is a continuous function, then the average value of f on the closed interval [a, b] is
Answers
The average value of a continuous function f on the closed interval [a, b] is equal to the definite integral of f over [a, b], divided by the length of the interval [a, b].
Let f(x) be a continuous function on the interval [a, b]. The average value of f on [a, b] is given by:
AVG = (1/(b-a)) * ∫[a, b] f(x) dx
where ∫[a, b] f(x) dx denotes the definite integral of f(x) over [a, b]. The length of the interval [a, b] is given by (b-a). Therefore, the average value of f on [a, b] is the ratio of the definite integral of f over [a, b] to the length of the interval [a, b]. This formula holds for any continuous function f on [a, b].
For more questions like Integral click the link below:
https://brainly.com/question/22008756
#SPJ11
Which fraction is not equivalent to 7/8

Answers
Answer:
C. 15/16
Step-by-step explanation:
A. Divide by 3
B. Divide by 5
C. Can't divide by anything.
D. Divide by 4
Answer:
C
Step-by-step explanation:
21/24 = 7/8
35/40 = 7/8
7/8 ≠ 15/16
14/16 ≠ 15/16
28/32 = 7/8
Factor the following:
x^2 - 9
Answers
Answer:
(x + 3)(x - 3)
Step-by-step explanation:
\( {x}^{2} - 9 \\ = {x}^{2} - {3}^{2} \\ = (x + 3)(x - 3)\)
a rocket is launched from a tower. the height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation. using this equation, find the time that the rocket will hit the ground, to the nearest 100th of second. y = − 16x^2 + 89x+ 50
Answers
The answer is:5.56 seconds (rounded to the nearest 100th of a second).Given,The equation that describes the height of the rocket, y in feet, as it relates to the time after launch, x in seconds, is as follows: y = − 16x² + 89x+ 50.
To find the time that the rocket will hit the ground, we must set the height of the rocket, y to zero. Therefore:0 = − 16x² + 89x+ 50. Now we must solve for x. There are a number of ways to solve for x. One way is to use the quadratic formula: x = − b ± sqrt(b² − 4ac)/2a,
Where a, b, and c are coefficients in the quadratic equation, ax² + bx + c. In our equation, a = − 16, b = 89, and c = 50. Therefore:x = [ - 89 ± sqrt( 89² - 4 (- 16) (50))] / ( 2 (- 16))x = [ - 89 ± sqrt( 5041 + 3200)] / - 32x = [ - 89 ± sqrt( 8241)] / - 32x = [ - 89 ± 91] / - 32.
There are two solutions for x. One solution is: x = ( - 89 + 91 ) / - 32 = - 0.0625.
The other solution is:x = ( - 89 - 91 ) / - 32 = 5.5625.The time that the rocket will hit the ground is 5.5625 seconds (to the nearest 100th of a second). Therefore, the answer is:5.56 seconds (rounded to the nearest 100th of a second).
For more question on equation
https://brainly.com/question/17145398
#SPJ8
The time that the rocket would hit the ground is 2.95 seconds.
How to determine the time when the rocket would hit the ground?Based on the information provided, we can logically deduce that the height (h) in feet, of this rocket above the ground is related to time by the following quadratic function:
h(t) = -16x² + 89x + 50
Generally speaking, the height of this rocket would be equal to zero (0) when it hits the ground. Therefore, we would equate the height function to zero (0) as follows:
0 = -16x² + 89x + 50
16t² - 89 - 50 = 0
\(t = \frac{-(-80)\; \pm \;\sqrt{(-80)^2 - 4(16)(-50)}}{2(16)}\)
Time, t = (√139)/4
Time, t = 2.95 seconds.
Read more on time here: brainly.com/question/26746473
#SPJ1
Write an algebraic equation for the following.
A number raised to the fifth power is four less than ten times the number.
A. 5x = 10x - 4
B. x³ =4-10x
C. 5x4-10x
D. x³ = 10x-4
Answers
Answer:
a
Step-by-step explanation:
raise to five
less than
ten times
How do I solve this equation?

Answers
Answer:
Step-by-step explanation:
This is called "solving an inequality".
The inequality can flip:
< becomes >
> becomes <
≤ becomes ≥
≥ becomes ≤
This only happens when we multiply or divide both sides by a negative number, or when we swap everything from either sides.
The thing to remember if there are two of the inequalities, we have to do everything to both sides. The goal stays the same. Get the "X" by itself in the middle.
-17 < 5 - 2x <= 9
-5 -5 -5
------------------------
-22 < -2x <= 4
Now we have to divide the -2 on both sides. Remember! Dividing by a negative means we have to FLIP THE SIGNS!
-22 < -2x <= 4
/-2 /-2 /-2
----------------------
11 > x >= -2
And your final answer would be that.
It can also be written this way:
-2 <= x < 11
Answer:
11 > x >= -2
Step-by-step explanation:
Explain whether or not the following table of values included a solution to the system of linear equations it represents.

Answers
Yes, the table contains the solution of the system of equations, and the solution is (7, 6).
The table of values incluedes a solution for the system of equations?Here we have a table that defines a system of equations of the form:
ya = f(x)
yb = f(x)
And a solution of that system is a point of the form:
yb = f(x) = ya
So we wan to find a pair such that for the same value of x, the values of ya and yb are the same ones.
We can see that when x = 6 that happens, then yes, the table has the solution to the system of equations, and the solutions is (6, 7)
Learn more about systems of equations at:
https://brainly.com/question/13729904
#SPJ1
pls help me fast! i need help!

Answers
Answer:
heres the answer with work

What are the solutions of the inequality 2x² x 6 0?
Answers
The solutions of the inequality \(2x^{2} + x - 6 = 0\) are 3/2, -2. This can be found by using the Quadratic Formula, which states that for any quadratic equation of the form \(ax^{2} +bx + c = 0\), the solutions are \(x = -b +/-\sqrt{b^{2} -4ac} /2a\).
Discriminant: b² - 4 a c = 1 - 4(2)(-6) = 1 + 48 = 49
Solution 1: x = \(-b + \sqrt{b^{2} -4ac} /2a\) = (-1 + √49)/(2×2) = (-1 +7)/4 = 6/4 = 3/2
Solution 2: x = \(-b-\sqrt{b^{2} -4ac} /2a\)= (-1 - √49)/(2×2) = -8/4 = -2
So, the two solutions are 3/2 and -2.
The equation can also be written as,
\(2x^{2} +4x -3x-6=0\)
\(2x(x+2) -3(x+2) = 0\)
\((2x-3)(x+2) = 0\)
x = 3/2, -2
To know more about solutions:
https://brainly.com/question/30089986
#SPJ4
which of the following is equal to sin(300)
Answers
Sin(300°) = -√3 / 2 .
need help ASAPP and show your work ( will rate 5 starts )

Answers
The cosine model is y = - 7 + 10 · cos (π · x/30 - π).
The sine model is y = - 7 + 10 · sin (π · x/30 - π/2).
How to find sinusoidal functions from a given graph
Sinusoidal functions are periodic trascendent expressions which involves trigonometric functions. There are two kinds of sinusoidal functions:
\(y = A \cdot \cos (B\cdot x + C) + D\) (1)
\(y = A\cdot \sin (B\cdot x + C) + D\) (2)
Where:
A - AmplitudeB - Angular frecuencyC - Angular phaseD - MidpointFirst, we find the amplitude and the midpoint:
A = [3 - (- 17)]/2
A = 10
D = [3 + (- 17)]/2
D = - 7
Now we find the angular phase and the angular frequency for each model:
Cosine model (x, y) = (0, - 17), (x, y) = (30, 3)
- 17 = 10 · cos C - 7 (3)
3 = 10 · cos (30 · B + C) - 7 (4)
By (3):
- 10 = 10 · cos C
cos C = - 1
C = acos(- 1)
C = - π
And by (4):
3 = 10 · cos (30 · B - π) - 7
10 = 10 · cos (30 · B - π)
cos (30 · B - π) = 1
30 · B - π = acos 1
30 · B - π = 0
30 · B = π
B = π/30
The cosine model is y = - 7 + 10 · cos (π · x/30 - π).
Sine model
Obtain the sine model by using trigonometric expressions:
cos θ = sin (θ + π/2) (5)
By (5):
y = - 7 + 10 · sin (π · x/30 - π + π/2)
y = - 7 + 10 · sin (π · x/30 - π/2)
The sine model is y = - 7 + 10 · sin (π · x/30 - π/2).
To learn more on sinusoidal functions: https://brainly.com/question/12060967
#SPJ1
Manuel works mowing lawns and babysitting. He earns $8.40 an hour for mowing and $7.60 an hour for babysitting. How much will he earn for 1 hour of mowing and 5 hours of babysitting?
Answers
Answer:
$14.10
Step-by-step explanation:
Answer:
$14.10
Step-by-step explanation:
An object is launched at 9.8 meters per second (m/s) from a 308.7-meter tall platform. The function that represents the object's height s at time t seconds after launch is
s(t) = −4.9t2 + 9.8t + 308.7,
where s is in meters. When does the object strike the ground?
Answers
this is the full answer for you're Q
please give me good


The time taken by the object to hit the ground will be 9 seconds.
What is a quadratic equation?A quadratic equation is a polynomial with a degree of 2 or the maximum power of the variable is 2 in quadratic equations. It has two solutions as its maximum power is 2.
Given that an object is launched at 9.8 meters per second (m/s) from a 308.7-meter tall platform. The function that represents the object's height s at time t seconds after launch is
s(t) = −4.9t²+ 9.8t + 308.7
To find the time taken put the function equal to zero.
−4.9t²+ 9.8t + 308.7 = 0
t² - 2t - 63 = 0
t² - 9t + 7t - 63 = 0
t ( t - 9 ) +7 ( t - 9 ) = 0
( t - 9 ) ( t + 7 ) = 0
t = 9 and -7(ignore)
t = 9 seconds
Therefore, the time taken by the object to hit the ground will be 9 seconds.
To know more about a quadratic equation follow
https://brainly.com/question/2264627
#SPJ2
The line plot shows the number of hours students in Mrs. Timberlake’s class worked on a project. How many students are included in the data?

Answers
Answer:
15
Step-by-step explanation:
I got this answer because I just added up all the x's.
1=3
2=2
3=5
4=3
5=2
3+2= 5
5+5=10
10+3=13
13+2=15
Leroy deposits £230 into an account which pays 5 percent simple interest per year.
How much will be in the account after one year?
Please help>"
Answers
Answer:
Amount in account after one year = £241.5
Step-by-step explanation:
Given:
Amount deposit into bank = £230
Rate of yearly interest = 5% Simple interest per year
Number of year = 1 year
Find:
Amount in account after one year
Computation:
Simple interest = Amount deposit x Rate of yearly interest x Number of year
Simple interest = 230 x 5% x 1
Simple interest = 230 x 0.05
Simple interest = £11.5
Amount in account after one year = Amount deposit into bank + Simple interest
Amount in account after one year = 230 + 11.5
Amount in account after one year = £241.5
For this experiment you have been randomly assigned to a group consisting of you and one other person. You do not know now, nor will you ever know, who this other person is. For this experiment all you have to do is distribute your 10 points into two accounts. One account called KEEP and one account called GIVE. The GIVE account is a group account between you and your group member. For every point that you (or your group member) put in the GIVE account, I will add to it 50% more points and then redistribute these points evenly to you and your group member. The sum of the points you put in KEEP and GIVE must equal the total 10 points. Any points you put in the KEEP account are kept by you and are part of your score on this experiment. Your score on the experiment is the sum of the points from your KEEP account and any amount you get from the GIVE account. For example, suppose that two people are grouped together. Person A and Person B. If A designates 5 points in KEEP and 5 points in GIVE and person B designates 10 points to KEEP and 0 points to GIVE then each person’s experiment grade is calculated in this manner: Person A’s experiment grade = (A’s KEEP) + 1.5(Sum of the two GIVE accounts)/2 = 5 +(1.5)(0+5)/2= 5 + 3.75 = 8.75. Person A’s score then is 8.75 out of 10. Person B’s experiment grade = (B’s KEEP) + 1.5(Sum of the two GIVE accounts)/2 = 10 +(1.5)(0+5)/2 = 10 + 3.75. Person B’s score then is 13.75 out of 10. (you can think of any points over 10 as extra credit) In this module’s activity you were asked to make a decision about how to invest your resources (points). This activity is a classic strategic game where the good of the individual is at odds with the good for the group. These problems are pervasive in risk management. For example, a physician who is trained to treat diseases may be reluctant to discuss alternative treatments with a patient when the physician is sure that a specific treatment is the only truly viable treatment. Nonetheless, you have learned in this course that physicians (or an agent of the physician) must have this discussion and bow to the will of the patient even if, in the physician’s judgment, the patient chooses an alternative treatment which is likely to be superfluous. In this way, informed consent and patient education are nuisances to the physician but are very important to protect the group (maybe a hospital or surgical group) from liability. In light of recent events another example is warranted. Individuals may choose to not get vaccinated since they do not want to bear the risk of any possible adverse side-effects of a vaccine. This is perfectly reasonable to do so. The problem arises when large groups of people choose to not get vaccinated thus making the impact of the disease relatively larger than need be if everyone would choose to take a vaccine (remember our first cost-benefit experiment). This implies that individual’s rights to choose not to vaccinate are at odds with what is good for the group of individuals. These types of problems are common in risk management. Discussion: (If you post your answers to each of the four questions below before the deadline, you will get the full ten points for the discussion. The questions do not need to be answered mathematically or with a calculation. If you feel the need to use mathematics to make a calculation, then you are free to do so but the questions are merely asking you for a number and how you arrived at that number. If you do not do any calculations to arrive at the number, just say how you arrived at the number. (There are no incorrect answers.) 1. In this activity how did you arrive at your decision on the keep-give split? 2. What is the best outcome of this situation for you? 3. What is the best outcome of this situation for the group? 4. Can you see any parallels with this game and how risk management strategies work? Explain.
Answers
1. I based my decision on allocating points to maximize my own score, while also considering the potential benefits of contributing to the group fund.
2. The best outcome for me would be allocating the minimum points required to the GIVE account, while putting the majority in the KEEP account. This would ensure I receive the most points for myself.
3. The best outcome for the group would be if both participants maximized their contributions to the GIVE account. This would create the largest group fund, resulting in the most redistributed points and highest average score.
4. There are parallels with risk management strategies. Individuals may act in their own self-interest, but a larger group benefit could be achieved if more participants contributed to "group" risk management strategies like vaccination, safety protocols, insurance policies, etc. However, some individuals may free ride on others' contributions while benefiting from the overall results. Incentivizing group participation can help align individual and group interests.
Find the approximate surface-area-to-volume ratio of a bowling ball with a radius of 5 inches. A. 0.6 B. 0.67 C. 1.67 D. 25 Please select the best answer from the choices provided A B C D
Answers
The approximate surface-area-to-volume ratio of a bowling ball with a radius of 5 inches is 0.6
To find the approximate surface-area-to-volume ratio of a bowling ball with a radius of 5 inches, we will first calculate the surface area (SA) and volume (V) of the ball, and then divide the surface area by the volume.
Step 1: Calculate the surface area (SA) using the formula for the surface area of a sphere:
\(SA = 4 πr^2\)
\(SA = 4 π5^2\)
\(SA = 4 π(25)\)
\(SA=100π\)
Step 2: Calculate the volume (V) using the formula for the volume of a sphere:
\(V = \frac{4}{3} π (r)^{3}\)
\(V = \frac{4}{3} π (5)^{3}\)
\(V = \frac{4}{3} π (125)\)
V = 166.67 π cubic inches
Step 3: Calculate the surface-area-to-volume ratio (SA/V)
\(\frac{SA}{V} = \frac{100}{166.67}\)
\(\frac{SA}{V}=\frac{100}{166.67}\)
\(\frac{SA}{V}= 0.6\)
So the approximate surface-area-to-volume ratio of a bowling ball with a radius of 5 inches is 0.6. The best answer from the choices provided is A.
To know more about "volume of a sphere" refer here:
https://brainly.com/question/30522025#
#SPJ11
1. Jacob put six numbered tiles into a bag. The
tiles are shown below.
19
12 18 17 18 9
He then reaches into the bag and pulls out one
tile. What is the probability that the tile he
pulled has the number 18?
Answers
The probability that the tile he pulled has the number 18 is,
⇒ 1 / 3
We have to given that;
Jacob put six numbered tiles into a bag.
And, The tiles are shown below.
19 12 18 17 18 9
Since, He reaches into the bag and pulls out.
Hence, Total number of tiles = 6
So, The probability that the tile he pulled has the number 18 is,
⇒ 2 / 6
Because there are 2 tile for number 18.
⇒ 1 / 3
Thus, The probability that the tile he pulled has the number 18 is,
⇒ 1 / 3
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ1
Stokes' Theorem Let S be an oriented smooth surface that is bounded by a simple closed smooth boundary curve C with positive orientation. Then for a vector field F, we have [F F. dr = = [1₁₂ ₁₁ curl F. dS 1. In this problem we will use Stokes' Theorem to help us evaluate II curl F. dS where F = (y. -1,³y) and S is the upper half of the sphere of radius 3 with upwards orientation. (a) Stokes' Theorem says F.. F. dr = = ff. cu curl F ds, so if we're using the theorem that means we will evaluate the line integral instead. To begin, sketch the surface S and identify its boundary curve C. (b) By drawing the hemisphere S, we can see that its boundary curve C is the circle of radius 3 in the ry-plane, with the usual counter-clockwise orientation. We can parameterize C by r(t) = (c) Next we'll work on the set up for the line integral. Remember the evaluation formula for a vector line integral: [F. ir = [ "F F(r(t)) - r' (t) dt (t) = F(x, y, z)= r' (t) F(r(t)) Find the dot product F(r(t))-r' (t) and simplify it as much as possible. (d) Evaluate the line integral [*F(r(1)) - r' (1) dt. (e) According to Stokes' Theorem, this tells us that the original flux integral cur curl F-dS=_ F. dr =
Answers
(a) To sketch the surface S, we consider the upper half of the sphere of radius 3. b) The boundary curve C is x² + y² = 9. c) the parameterization of C is r(t) = (3cosθ, 3sinθ, 0). d) The line integral is -9sin²θ - 3cosθ. e) The original flux integral is -9π/4.
(a) To sketch the surface S, we consider the upper half of the sphere of radius 3. The orientation is upwards, indicating that the normal vectors are pointing outward. The surface S can be represented as the portion of the sphere with z ≥ 0.
(b) The boundary curve C is the circle of radius 3 in the xy-plane, given by the equation x² + y² = 9. The orientation of C is counter-clockwise when viewed from above.
(c) To parameterize C, we can use polar coordinates. Let's choose θ as the parameter ranging from 0 to 2π. Then, the parameterization of C is:
r(t) = (3cosθ, 3sinθ, 0)
(d) To evaluate the line integral, we need to find the dot product F(r(t)) · r'(t) and simplify it:
F(x, y, z) = (y, -1, 3y)
r(t) = (3cosθ, 3sinθ, 0)
Substituting these values into F and r'(t):
F(r(t)) = (3sinθ, -1, 3(3sinθ))
r'(t) = (-3sinθ, 3cosθ, 0)
Taking the dot product:
F(r(t)) · r'(t) = (3sinθ)(-3sinθ) + (-1)(3cosθ) + (3(3sinθ))(0)
= -9sin²θ - 3cosθ + 0
= -9sin²θ - 3cosθ
(e) To evaluate the line integral, we need to compute:
∫[F(r(t)) - r'(t)] dt
Substituting the expressions for F(r(t)) and r'(t):
∫[-9sin²θ - 3cosθ] dt
To evaluate this integral, we need to specify the limits of integration, which correspond to the range of θ. Since we're considering the full circle, the limits are 0 to 2π:
∫[F(r(t)) - r'(t)] dt = ∫[-9sin²θ - 3cosθ] dθ (from 0 to 2π)
Integrating term by term:
= [-9∫sin²θ dθ] - [3∫cosθ dθ] (from 0 to 2π)
Using trigonometric identities, we have:
= [-9(θ/2 - sin(2θ)/4)] - [3sinθ] (from 0 to 2π)
Plugging in the limits of integration:
= [-9(2π/2 - sin(4π)/4)] - [3sin(2π)] - [-9(0/2 - sin(0)/4)] - [3sin(0)]
Simplifying, we get:
= [-9π + 9π/4] - [0] - [0] - [0]
= -9π/4
Therefore, the line integral is -9π/4.
According to Stokes' Theorem, this tells us that the original flux integral ∬curl F · dS is also equal to -9π/4.
To learn more about curve here:
https://brainly.com/question/32524810
#SPJ4
Does anybody knows what’s the Pi for for this answer?
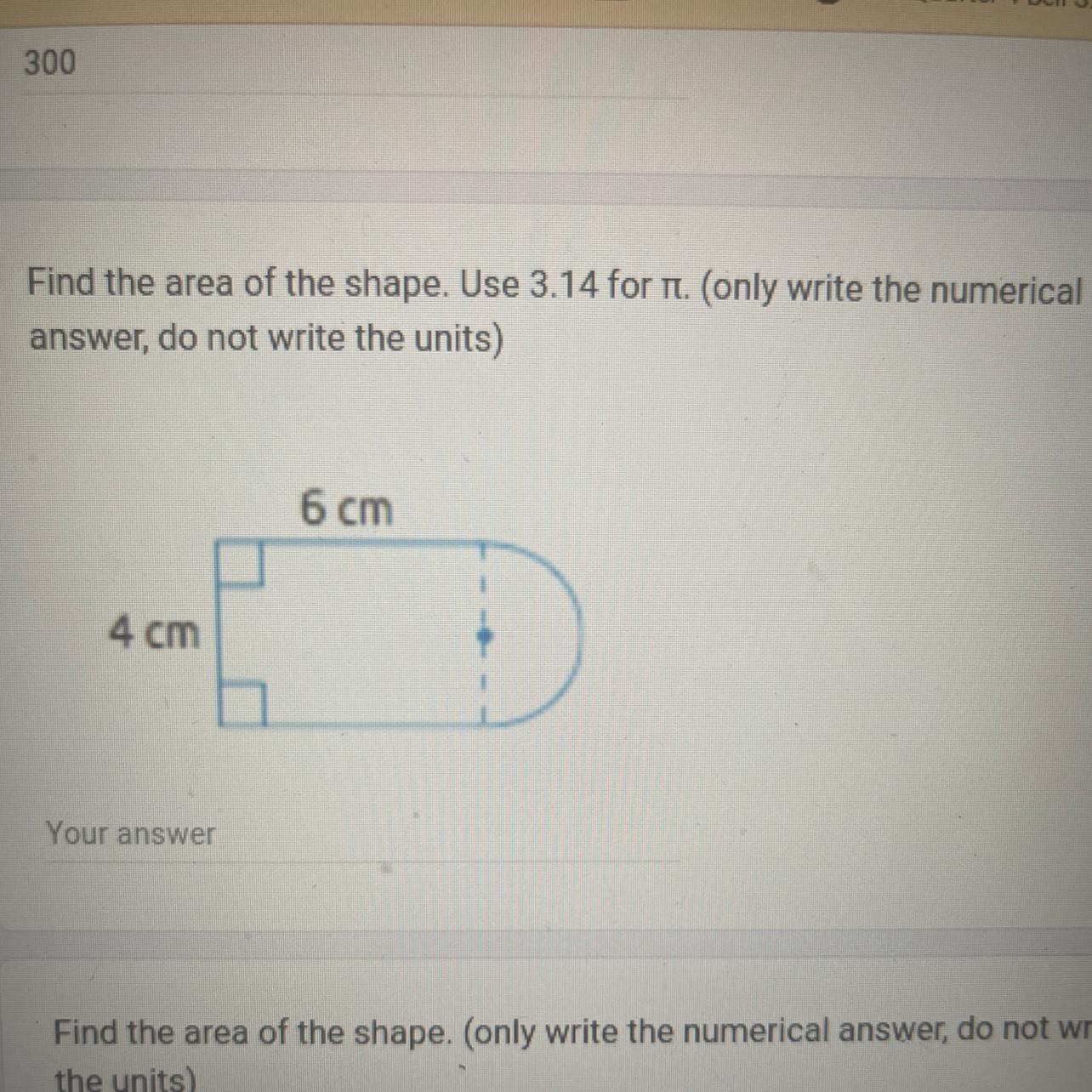
Answers
In a nutshell, pi is the ratio of a circle's diameter to its circumference. It is written as the Greek letter p, or. This ratio will always equal pi, no matter how big the circle is. The value of pi is around 3.14 in decimal notation.
Why pi in the formula?Circumference and diameter of a circle are related by the Pi formula. If the diameter and circumference of a circle are known, it can be used to compute the value of pi. Pi is a Greek letter with the symbol, and in geometry, it represents the proportion of a circle's diameter to its circumference.
The Greek word perimitros, which means "perimeter," begins with the letter pi, which is why [the Welsh mathematician] William Jones gave it the name "pi" in 1706.
A circle is used to calculate the ratio known as pi. The value of pi is given by = Circumference/Diameter if the diameter and circumference of a circle are known.
Therefore pi of this is \(30.3 cm^{2}\) .
To learn more about pi value refer to :
https://brainly.com/question/15962176
#SPJ1
A bus drives for 3½ hours at an average speed of 56 mph. How far does the bus drive?
Answers
distance = speed x time
where speed is given in miles per hour (mph) and time is given in hours.
In this case, the speed of the bus is 56 mph and the time it travels is 3.5 hours. So we can calculate the distance it travels as:
distance = speed x time
distance = 56 mph x 3.5 hours
distance = 196 miles
Therefore, the bus drives a distance of 196 miles.
Answer:
196 miles
Step-by-step explanation:
To find the distance that the bus drives, we can use the formula:
distance = rate x time
where rate is the average speed and time is the duration of the trip.
In this case, the average speed of the bus is 56 mph and the duration of the trip is 3 1/2 hours. However, it is easier to work with time in terms of a single unit, so let's convert 3 1/2 hours to 7/2 hours:
3 1/2 hours = (2 x 3) + 1/2 hours = 7/2 hours
Now we can plug in the values into the formula:
distance = rate x time
distance = 56 mph x 7/2 hours
We can simplify by multiplying 56 by 7 and then dividing by 2:
distance = (56 x 7) / 2 = 196 miles
Intercept Form
Point (-3,4)
Slope 5/3
m= b=
Answers
Answer:
y = 5/3x + 9
Step-by-step explanation:
y = 5/3x + b
4 = 5/3(-3) + b
4 = -5 + b
9 = b
Joe moves a 10 kg weight 5 meters with a force of 50 N in 10 seconds. Leroy uses the same force to move the same weight the same distance in 7.5 seconds? Who has more power and why
Answers
Answer:
10 sec
Step-by-step explanation:
100 points pls right answers only it’s for apex
An outlier point is added to a set of bivariate data. In what way must your analysis change with the addition of the outlier?
A. The sign of the regression coefficient will change from positive to
negative, or vice versa.
B. The value of the correlation coefficient will move closer to 0.
C. The regression constant will change dramatically.
D. All of the above.
Answers
Answer:
I already said b in the comment area so I'm just putting it here now
Step-by-step explanation:
(B) The value of the correlation coefficient will move closer to 0.
Bivariate data:Bivariate data in statistics refers to data on two variables, each of which has a value coupled with a value of the other variable. Normally, it would be interesting to look into any potential relationships between the two variables. The association can be investigated using sample statistics that can be utilized for inference, a tabular or graphical display, or both. The approach taken to look into the association would depend on how the variable was measured. Bivariate correlation or bivariate association are terms used to describe the links, which only involve two variables.Therefore, the correct option is (B) The value of the correlation coefficient will move closer to 0.
Know more about Data here:
https://brainly.com/question/19243813
#SPJ2
What is the slope of the line?
A.) 1
B.) 1/2
C.) -2
D.) 2

Answers
Answer:
D
Step-by-step explanation:
What is the measure of one base angle in an isosceles right triangle?
Answers
If one angle in an isosceles triangle is 90 degrees then the measure of each angle of an isosceles triangle will be 45 degrees
What is an isosceles triangle?
A triangle with two equal sides is said to be an isosceles. Also equal are the two angles that face the two equal sides. In other terms, an isosceles triangle is a triangle with two sides that have the same length.
If the sides AB and AC of a triangle ABC are equal, then the triangle ABC is an isosceles triangle with B = C. "If the two sides of a triangle are congruent, then the angle opposite to them is likewise congruent," states the theorem that characterizes the isosceles triangle.
Since this triangle's two sides are equal, the base of the triangle is the side that is not equal.The triangle's two equal sides' opposing angles are always equal.The vertex (topmost point) of an isosceles triangle is where the height of the triangle is calculated.The third angle of a right isosceles triangle is 90 degrees.As we know that in an isosceles triangle set of two angles is equal
And
we also know that sum of all the angles of a triangle is 180 degrees
So, According to the question
90 degrees + other angles =180 degrees
other angles = 90 degrees
one angle = 90/2
one angle = 45 degree
Learn more about the Isosceles triangle from the link below
brainly.com/question/2456591
#SPJ4
control limits are based on multiples of the process standard deviation. question 11 options: true false
Answers
Control limits are based on multiples of the sample statistic's standard deviation, hence the assertion is false that "control limits are based on multiples of the process standard deviation".
A control chart is made up of many different parts. There are two control limitations. The top dashed line represents the upper control limit (UCL), and the bottom dashed line represents the lower control limit (LCL).The solid middle line denotes the statistic's average for the plot.
The horizontal lines known as control limits in a control chart show the upper and lower limits of the acceptable range of results for a process. When plotted data goes over a control limit, a process is out of control and requires management action. The control limits are defined as three standard deviations on either side of the mean.
Visit here to learn more about Standard deviation: https://brainly.com/question/23907081
#SPJ4
worth a brainliest !!!! Answer quixk
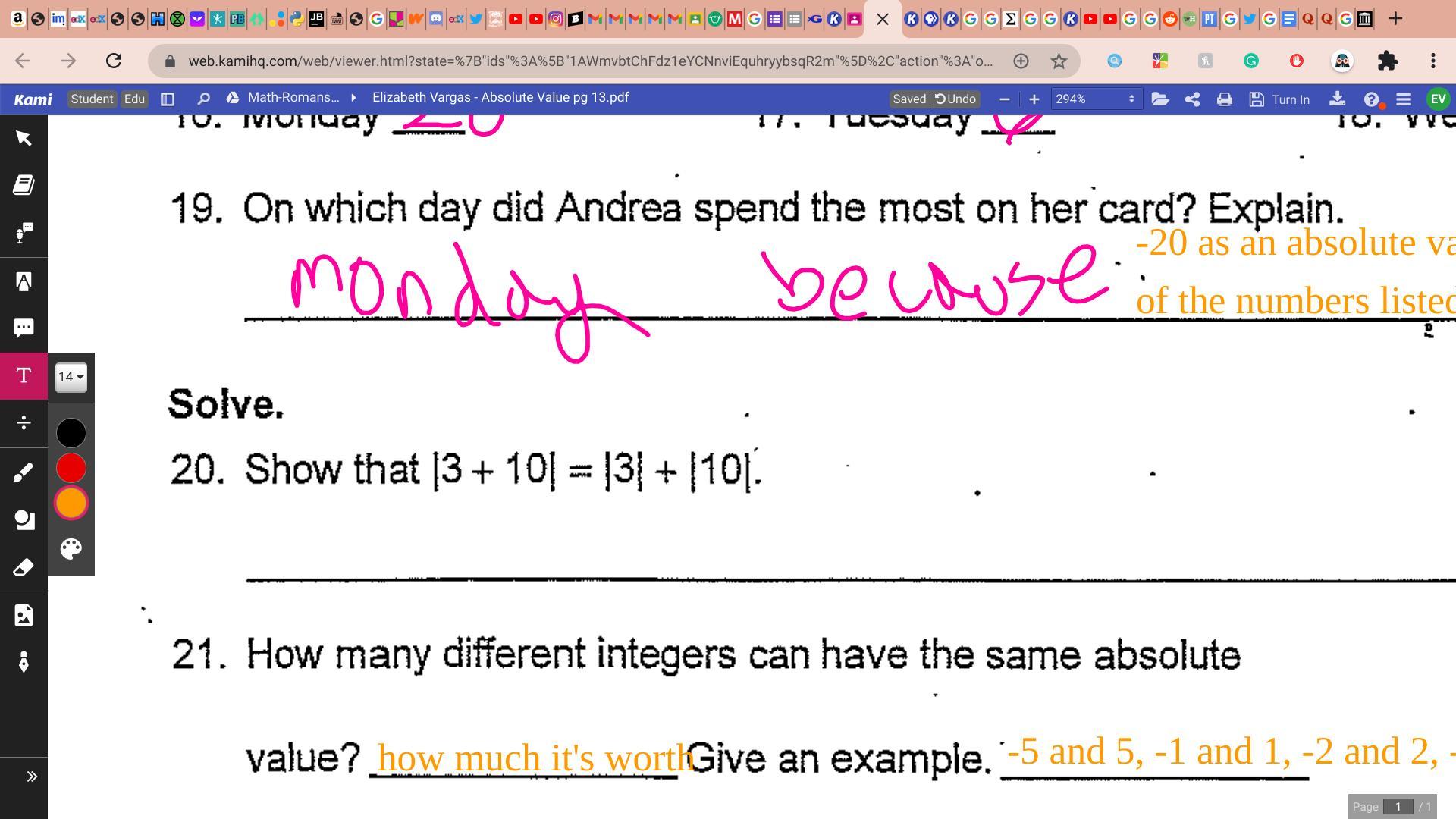
Answers
Answer:
20.
|3 + 10| = |13| = 13
|3| + |10| = 3 + 10 = 13
Both equal 13.
a+history+test+has+30+questions.+a+student+answers+90%+of+the+questions+correctly.+how+many+questions+did+the+student+answer+correctly?
Answers
The student answered 27 out of 30 questions correctly on the history test, achieving a 90% accuracy rate.
To calculate the number of questions the student answered correctly, we can multiply the total number of questions (30) by the percentage of questions answered correctly (90%). The calculation is as follows:
Number of questions answered correctly = Total number of questions × Percentage of questions answered correctly
= 30 × 0.90
= 27
Therefore, the student answered 27 questions correctly on the history test.
To learn more about Percentage click here :
brainly.com/question/14318030
#SPJ11