A car maker claims that its new sub-compact car gets better than 47 miles per gallon on the highway. Determine whether the hypothesis test is left-tailed, right-tailed or two-tailed.
Answers
The hypothesis by the carmaker is one-tailed.
What is a one-tailed hypothesis?A one-tailed hypothesis is a claim that a given parameter is sure to increase or decrease. The carmaker says that the new sub-compact car gets better than 47 miles. This means that there is a certainty of the speed exceeding 47 miles.
This hypothesis is a one-tailed assumption. A two-tailed hypothesis will rather compare the changes that occur within the parameter than assign an increase or decrease claim. So, the above hypothesis is one-tailed.
Learn more about the one-tailed hypothesis here:
https://brainly.com/question/14053535
#SPJ1
Related Questions
five hamburgers cost 5.25 at this rate what is the cost of 8 hamburgers
Answers
Answer: 8.4
Step-by-step explanation: 5.25 divided by 5 is 1.05. So 1.05 x 8 is 8.4
2. Price of 1 is 1.05
3. 1.05 multiply by 8 is 8.40
ANSWER: $8.40 for 8
b.
Assume the trend in the numbers of users tripling each year was true for all years from 2001 to
2009. Complete the table below using 2005 as year 1 with 3 million as the number of users that
year.
-3
-2
-1
0
1
2
3
4
5
Year
# of
users in
millions
3
Answers
I need help! +21 points
Kiki has a piece of string that she cuts into smaller pieces. This line plot shows the lengths of the pieces. Raj has a piece of string that is 1/2 as long as Kiki's third-longest piece. (Note: The problem says third-longest piece, not third-longest length.)
How long is Raj's piece of string?
Enter your answer as a mixed number in simplest form by filling in the boxes.

Answers
The length of Raj's string is 54 in long.
How to solveA dot chart or dot plot is a statistical chart consisting of data points plotted on a fairly simple scale, typically using filled in circles. There are two common, yet very different, versions of the dot chart.
Given that, Kiki has a piece of string that she cuts into smaller pieces. This line plot shows the lengths of the pieces. Raj has a piece of string that is 12 as long as Kiki's third-longest piece.
The third-longest piece = 4 1/2 in
The length of Raj's string = 4 1/2 x 12 = 9/2 x 12 = 54
Hence, the length of Raj's string is 54 in long.
Read more about length here:
https://brainly.com/question/28108430
#SPJ1
A well is to be dug at the location in the diagram. Use the diagram for the parts.
The equation that represents the road is y= ______
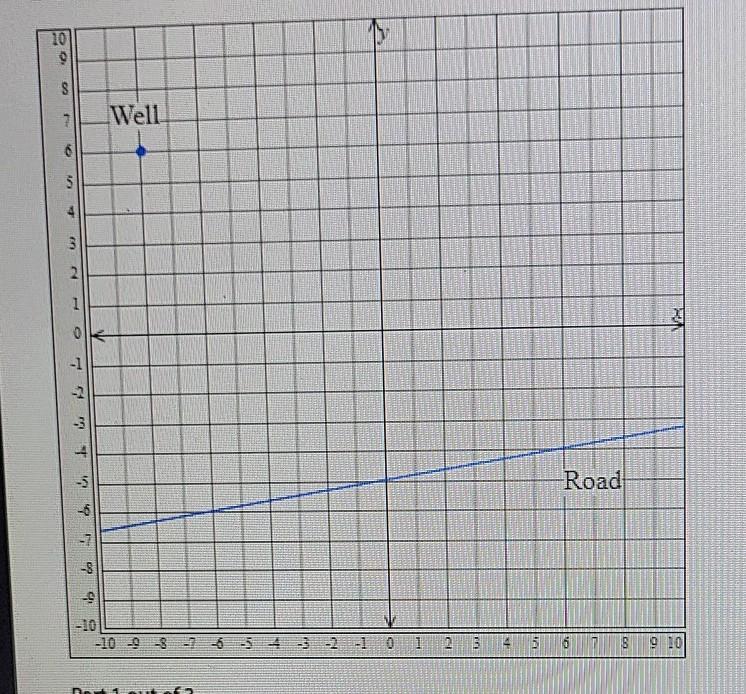
Answers
Answer:
\( y = \frac{1}{6}x - 5 \)
Step-by-step explanation:
The equation that represents the road can be written as \( y = mx + b \)
Find, m = slope, and b = y-intercept of the line.
Using two points on the line, (-6, -6) and (6, -4), find the slope:
\( slope(m) = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-4 -(-6)}{6 -(-6)} = \frac{2}{12} = \frac{1}{6} \)
Substitute x = -6, y = -6, and m = ⅙ into \( y = mx + b \) to find b.
\( -6 = \frac{1}{6}(-6) + b \)
\( -6 = -1 + b \)
Add 1 to both sides
\( -6 + 1 = b \)
\( -5 = b \)
Substitute m = ⅙, and b = -5 into \( y = mx + b \).
✅The equation that represents the road would be:
\( y = \frac{1}{6}x + (-5) \)
\( y = \frac{1}{6}x - 5 \)
Susan pushes a box up an inclined plane doing 50 Joules of work. The output work was calculated to be 25 loules. Find the efficiency of this inclined plane
A) 25%
B) 50%
C)100%
D) 200%
Answers
A) 25%
B) 50%
C)100%
D) 200%
A.25%
There are 2.54 centimeters in 1 inch. Show Many centimeters are there in 1 foto?
Answers
Answer:
30.48 cm
Step-by-step explanation:
One foot has 12 inches. To find number of centimeters in a foot, multiply 12 by 2.54 and we get 30.48 cm.
A student solved this problem and said the answer was 5 1 4 14 miles. Danielle ran 3 1 8 18 miles on Tuesday, 4 1 2 12 miles on Wednesday, and 5 1 4 14 miles on Thursday. How far did Danielle run altogether? Is the student's answer reasonable? No, the answer is not reasonable. It should be about 13 miles. Yes, the answer is reasonable. No, the answer is not reasonable. It should be about 2 miles. No, the answer is not reasonable. It should be about 20 miles.
Answers
Question
A student solved this problem and said the answer was \(5\frac{1}{4}\) miles. Danielle ran \(3\frac{1}{8}\) miles on Tuesday, \(4\frac{1}{2}\) miles on Wednesday, and \(5\frac{1}{4}\) miles on Thursday. How far did Danielle run altogether? Is the student's answer reasonable?
- No, the answer is not reasonable. It should be about 13 miles.
- Yes, the answer is reasonable.
- No, the answer is not reasonable. It should be about 2 miles.
- No, the answer is not reasonable. It should be about 20 miles.
Answer:
- No, the answer is not reasonable. It should be about 13 miles.
Step-by-step explanation:
Given
Student solution = \(5\frac{1}{4}\) miles.
Miles covered on Tuesday = \(3\frac{1}{8}\) miles
Miles covered on Wednesday = \(4\frac{1}{2}\) miles
Miles covered on Thursday = \(5\frac{1}{4}\) miles
Required
- Total distance covered by the student
- Is the student answer reasonable?
To calculate the actual distance covered by Danielle, we simply add the distance covered on each day,
This goes thus
Distance = \(3\frac{1}{8}\) + \(4\frac{1}{2}\) + \(5\frac{1}{4}\)
Convert to Improper Fractions
Distance = \(\frac{25}{8}\) + \(\frac{9}{2}\) + \(\frac{21}{4}\)
Take LCM
Distance = \(\frac{25 + 36 + 42}{8}\)
Distance = \(\frac{103}{8}\)
Distance = 12.875
From the calculations above, we can conclude that the student's answe is not reasonable because his calculation (\(5\frac{1}{4}\) miles) is much more smaller than the actual result 12.875 miles
From option A through D, Only option A is correct because 12.875 miles cam be approximated to 13 miles.
Hence,
A. - No, the answer is not reasonable. It should be about 13 miles.
is the right answer
Find the Total surface area
A prism 11 in tall with a right triangle for a base with side lengths 6 in, 8 in, and 10 in.
A) 344 in2
B) 383 in2
C) 312 in2
D) 288 in2
Answers
Answer:
You may not recognize this...but the base forms a "Pythagorean" right triangle with legs of 6 and 8 cm
The area of a right triangle is (1/2) ( product of leg lengths)
So...the area of the base = (1/2) (6 * 8 ) = (1/2) 48 = 24 cm^2
And the volume of the prism is just the base area x height = 24 x 7 = 192 cm^2
Step-by-step explanation:
a data analyst is working with the world happiness data in tableau. what tool do they use to select the area on the map representing finland? 1 point radial rectangular lasso pan
Answers
Pan tool do the data analyst use to select the area on the map representing Finland.
A data analyst is working with the world happiness data in table. To use Pan tool to select the area on the map representing Finland.
A data professional examines data to uncover critical insights about a company's consumers and how the data may be utilized to address problems. They also share this information with corporate executives and other stakeholders.
Pan allows us to shift the map to focus on it or present the areas in the way we wish. Simply pick the Pan Option and move the map around to suit your needs. Alternatively, you may move the map by holding down the Shift key.
To know more about data here
https://brainly.com/question/29677598
#SPJ4
Help please I don’t get it

Answers
a) The expected number of people to die before their 71st birthday is given as follows: 128.
b) The probability that a 67 year old woman will live to her 68th birthday is given as follows: 0.8876 = 88.76%.
How to calculate a probability?The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes.
0.025679 of the 70 year old men die, hence the expected number out of 5000 is given as follows:
0.025679 x 5000 = 128.
The probability for item b is given as follows:
0.016798/0.018925 = 0.8876 = 88.76%.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1
10. One contestant on a game show has
1,500 points and another contestant has
-250 points. What is the difference
between the scores of the contestants?
Answers
it's the difference between 1500 and -250, so simply add the two.
think about it like this:
one number is lower than zero, so you already have the 1500 minimum for a difference. but it isn't bang on zero, it's 250 less than that. so the answer is 1750.
Given r(x) =x' - 4x2 + 4x - 6, find the value of r(2). What does your answer tell you about x - 2 as a factor of r(x)? Explain.
Answers
We can conclude that the value of r(2) which is -6 and x - 2 is not the factor for r(x).
What is Factor?A function that accepts a real number as input, typically represented by the variable x and outputs another real number, typically the value of the function denoted by f is known as a real-valued function of a real variable (x).Any polynomial that is divisible by the polynomial P(x) is a factor of that polynomial (x).So, we know that the equation is:
r(x)=x^3-4x^2+4x-6:Now, calculate the equation when x = 2.
r(2)=2^3-4(2)^2+4(2)-6r(2)=8-16+8-6r(2)=-6Now, we can conclude that:
As we see that x=2 is not equal to zero.Implies x-2 does not divide r(x) evenly.Thus x-2 is not a factor of given r(x).Therefore, we can conclude that the value of r(2) which is -6 and x - 2 is not the factor for r(x).
Learn more about factors here:
brainly.com/question/24380382
#SPJ13
ac circular runway has a radius of 100 m.Find the distance covered by a person in one complete rotation .
Answers
Answer:
628m
Step-by-step explanation:
Given radius=100m
distance=circumference
=2pie r
=2×22/7×100
=628m
please mark me brainliest
Write an equation of the line passing through the points (3,5) and (-1. - 15).
Answers
Answer:
y = 5x - 10
Step-by-step explanation:
Answer:
y=20/4x-10
Step-by-step explanation:
(3, 5) (-1, -15)
-15-5/-1-3=20/4x
y=-10

suppose the time a child spends waiting at for the bus as a school bus stop is exponentially distributed with mean 6 minutes. determine the probability that the child must wait at least 8 minutes on the bus on a given morning. a) 0.2636 b) 0.4636 c) 0.5636 d) 0.5272 e) 0.2364 f) none of the above
Answers
The probability that the child must wait at least 8 minutes for the bus on a given morning is 0.2636
To determine the probability that a child must wait at least 8 minutes for the bus on a given morning, given that the waiting time is exponentially distributed with a mean of 6 minutes, we'll use the exponential distribution formula:
\(P(T > t) = e^{(-t/μ)}\)
where T is the waiting time, t is the specific time we are interested in (8 minutes in this case), μ is the mean waiting time (6 minutes), and e is the base of the natural logarithm (approximately 2.71828).
Step 1: Plug in the values into the formula:
\(P(T > 8) = e^{(-8/6)}\)
Step 2: Simplify the exponent:
\(P(T > 8) = e^{(-4/3)}\)
Step 3: Calculate the probability using the value of e:
\(P(T > 8) ≈ 2.71828^{(-4/3)} ≈ 0.2636\)
Therefore, the probability that the child must wait at least 8 minutes for the bus on a given morning is approximately 0.2636, which corresponds to option (a).
Learn more about probability here,
https://brainly.com/question/24756209
#SPJ11
dried apricots with 3.25 were mixed with dried prunes worth 4.79 to produce a mixture of dried fruit, how much each kind of fruit was used to produce 25 ponds
Answers
14.84 pounds of dried apricots were used and 10.16 pounds of dried prunes were used to produce 25 pounds of the dried fruit mixture.
Let's call the weight of dried apricots used in the mixture "x" (in pounds). Then the weight of dried prunes used in the mixture is 25 - x (in pounds).
The cost per pound of dried apricots is 3.25, and the cost per pound of dried prunes is 4.79. So the total cost of the mixture is:
3.25x + 4.79(25 - x) = 3.25x + 119.75 - 4.79x
Expanding both sides:
119.75 = 8.04x
Dividing both sides by 8.04:
x = 14.84 pounds
So 14.84 pounds of dried apricots were used in the mixture, and 25 - 14.84 = 10.16 pounds of dried prunes were used in the mixture.
To learn more about the Cost, visit:
brainly.com/question/29136200
#SPJ4
14.84 pounds of dried apricots were used and 10.16 pounds of dried prunes were used to produce 25 pounds of the dried fruit mixture.
Let's call the weight of dried apricots used in the mixture "x" (in pounds). Then the weight of dried prunes used in the mixture is 25 - x (in pounds).
The cost per pound of dried apricots is 3.25, and the cost per pound of dried prunes is 4.79. So the total cost of the mixture is:
3.25x + 4.79(25 - x) = 3.25x + 119.75 - 4.79x
Expanding both sides:
119.75 = 8.04x
Dividing both sides by 8.04:
x = 14.84 pounds
So 14.84 pounds of dried apricots were used in the mixture, and 25 - 14.84 = 10.16 pounds of dried prunes were used in the mixture.
To learn more about Cost
brainly.com/question/29136200
#SPJ4
in a neighborhood donut shop, one type of donut has 440 calories, five types of donuts have 350 calories, seven types of donuts have 530 calories, five types of donuts have 330 calories, and five types of donuts have 580 calories. find the range. calories find the standard deviation. round your answer to the nearest tenth, if necessary. calories
Answers
The range is 250 calories and the standard deviation is 57.5 calories.
In a neighbourhood donut shop, one type of donut has 440 calories, five types of donuts have 350 calories, seven types of donuts have 530 calories, five types of donuts have 330 calories, and five types of donuts have 580 calories
The formula for the range is given by;`
range = maximum value - minimum value`
The minimum value in this case is 330 and the maximum value is 580Therefore, `range = 580 - 330 = 250`
The formula for standard deviation is given by;`s = sqrt [Σ(x - µ)² / N]`
where Σ is a symbol of summation, x is the value, µ is the mean, N is the number of data and s is the standard deviation.
Calculate the mean (µ)`µ = Σ fx / N = 11960 / 23 ≈ 520.87`Substitute the values in the formula above and calculate;
Calories (x)fx(x - µ)² 3301750(-190.87)² 3501750(-170.87)² 440440(-80.87)² 5303710(9.13)² 5802900(59.13)²Total = 352191.55`s = sqrt (352191.55 / 23)≈ 57.5 calories
To know more about standard deviation refer to-
brainly.com/question/23907081#
#SPJ11
short answer: Write an equation in the form y=ax2+bx+c for a parabola that intersects the x-axis at -6 and 2 and passes through the point (1,-14) (2 points). Show you work.
Answers
Answer:
y = 2x^2 + 8x - 24
Step-by-step explanation:
This is a "working backwards" kind of a problem. You know the solution (the x-intercepts) and work backwards to find the equation. See image.

Find the x- and y-intercepts of the graph of the linear equation 3x+6y=24.
Answers
Answer:
y=0,4 and x=8,0
The x and y-intercept of the linear equation 3x + 6y = 24 will be (8,0) and (0,4) respectively.
What is a linear function?A straight line on the coordinate plane is represented by a linear function.
A linear function always has the same and constant slope.
The formula for a linear function is f(x) = ax + b, where a and b are real values.
As per the given linear function,
3x+6y=24
At x-intercept, y = 0
3x = 24
x = 8 thus it will be (8,0).
At y-intercept , x = 0
6y = 24
y = 4 thus it will be (0,4)
Hence "The linear equation 3x + 6y = 24 will have x-intercepts of (8, 0) and (0, 4) correspondingly".
For more about the linear function,
brainly.com/question/21107621
#SPJ2
The overall Chi-Square test statistic is found by________ all the cell Chi-Square values.a. dividingb. subtractingc. multiplyingd. adding
Answers
The overall value represents the degree of deviation between the observed and expected frequencies and is used to determine the p-value for the Chi-Square test statistic. Therefore, the correct option is (d) adding.
In a contingency table analysis, the chi-square test is used to determine whether there is a significant association between two categorical variables. The test involves comparing the observed frequencies in each cell of the table with the frequencies that would be expected if the variables were independent.
To calculate the chi-square test statistic, we first compute the expected frequencies for each cell under the assumption of independence. We then calculate the difference between the observed and expected frequencies for each cell, square these differences, and divide them by the expected frequencies to get the cell chi-square values.
To know more about Chi-Square test statistic,
https://brainly.com/question/16749509
#SPJ11
A square has an area that is less than 100m squared. what is a reasonable range for the graph of the square's side? A: 0
Answers
Answer:
0
Explanation:
Area of a square is expressed as;
A = L^2
L is the side length of the square
Given]Area A = 100m^2
Substitute inti= the formula
A < L^2
100 < L^2
L^2 > 100
L > \sqrt[100]
L > 10
Hence the range for the graph of the square's side is 0
What is another word that describes the zeros of a quadratic function.
Answers
A different term for a quadratic function's zeros is "roots." The zeros or roots of a quadratic function are the points on the x-axis where the function meets or crosses it.
They stand in for the x values at which the quadratic function equals zero. Depending on the discriminant of the quadratic equation, the zeros or roots of a quadratic function can either be real or complex integers. The quadratic has two unique real roots if the discriminant is positive. The quadratic has a single real root, also referred to as a double root or repeating root, if the discriminant is zero. The quadratic has two complex roots that can be represented as a + bi if the discriminant is negative.
learn more about quadratic here :
https://brainly.com/question/22364785
#SPJ11
What is the yield to maturity of a ten-year, $1000 bond with a 5.2% coupon rate and semi-annual coupons if this bond is currently trading for a price of $884?
5.02%
6.23%
6.82%
12.46%
G
5.20%
Answers
The yield to maturity of a ten-year, $1000 bond with a 5.2% coupon rate and semi-annual coupons, if the =bond is currently trading for a price of $884, is 6.23%. Thus, option a and option b is correct
Yield to maturity (YTM) is the anticipated overall return on a bond if it is held until maturity, considering all interest payments. To calculate YTM, you need to know the bond's price, coupon rate, face value, and the number of years until maturity.
The formula for calculating YTM is as follows:
YTM = (C + (F-P)/n) / ((F+P)/2) x 100
Where:
C = Interest payment
F = Face value
P = Market price
n = Number of coupon payments
Given that the bond has a coupon rate of 5.2%, a face value of $1000, a maturity of ten years, semi-annual coupon payments, and is currently trading at a price of $884, we can calculate the yield to maturity.
First, let's calculate the semi-annual coupon payment:
Semi-annual coupon rate = 5.2% / 2 = 2.6%
Face value = $1000
Market price = $884
Number of years remaining until maturity = 10 years
Number of semi-annual coupon payments = 2 x 10 = 20
Semi-annual coupon payment = Semi-annual coupon rate x Face value
Semi-annual coupon payment = 2.6% x $1000 = $26
Now, we can calculate the yield to maturity using the formula:
YTM = (C + (F-P)/n) / ((F+P)/2) x 100
YTM = (2 x $26 + ($1000-$884)/20) / (($1000+$884)/2) x 100
YTM = 6.23%
Therefore, If a ten-year, $1000 bond with a 5.2% coupon rate and semi-annual coupons is now selling at $884, the yield to maturity is 6.23%.
Learn more about yield to maturity
https://brainly.com/question/26376004
#SPJ11
Match the Vocab Word to the definition.
Remember, you are allowed to use your notes to help you!
Question 3 options:
If a = b, and c ≠ 0, then a/c = b/c
If a = b, then a + c = b + c
If a > b, and c > 0, then a/c > b/c
If a > b, and c < 0, then a/c < b/c
If a > b, then a - c > b – c
If a = b, then c ∙ a = c ∙ b
If a > b, and c > 0, then c ∙ a > c ∙ b
If a > b, and c < 0, then c ∙ a < c ∙ b
If a = b, then a - c = b - c
If a > b, then a + c > b + c
1.
Addition Property of Equality
2.
Subtraction Property of Equality
3.
Multiplication Property of Equality
4.
Division Property of Equality
5.
Addition Property of Order
6.
Subtraction Property of Order
7.
Multiplication Property of Order
8.
Division Property of Order
Answers
Match the Vocab Word to the definition
1. Addition Property of Equality
If a = b, then a + c = b + cIf a > b, then a + c > b + c2. Subtraction Property of Equality
If a = b, then a - c = b - cIf a > b, then a - c > b – c3. Multiplication Property of Equality
If a > b, and c > 0, then c ∙ a > c ∙ bIf a > b, and c < 0, then c ∙ a < c ∙ bIf a = b, then c ∙ a = c ∙ b4. Division Property of Equality
If a = b, and c ≠ 0, then a/c = b/cIf a > b, and c > 0, then a/c > b/cIf a > b, and c < 0, then a/c < b/cWhat is order property in math?Order property refers to situation of changing the order of the factors. swapping the positions of the addends still maintain the answer
For instance commutative property of addition
a + b = b + acommutative property of multiplication
a * b = b * aThe properties of equality refers to performing same operation in the opposite sides of an equation
Addition Property of Equality: here c is added to both sides of the equality such that a = b, then a + c = b + c
Learn more on property of equality at:
https://brainly.com/question/28293087
#SPJ1
If S = \(\frac{n}{2}\)(a + L), find n when, S= 640, a = 25 and L = 39
Answers
Answer:
n = 20
Step-by-step explanation:
Sum of an arithmetic series
\(S_n=\dfrac{n}{2}(a+l)\)
where:
a = first terml = last termn = number of termsGiven:
\(S_n=640\)\(a=25\)\(l=39\)Substituting the given values into the formula and solving for n:
\(\implies 640=\dfrac{n}{2}(25+39)\)
\(\implies 640 \cdot 2=n(25+39)\)
\(\implies 1280=n(25+39)\)
\(\implies 1280=64n\)
\(\implies n=\dfrac{1280}{64}\)
\(\implies n=20\)
Subtract 11/14-2/7?Make sure your answer is fully reduced.
Answers
Answer:
1/2
Step-by-step explanation:
turn 2/7 into 4/14 then subtract that from 11/14 and you get 7/14 and the also can go as 1/2
Three chains, each 14 feet in length, are
linked end to end. Two longer chains of
equal length are added to make a total
length of 100 feet. What is the length of
one of the longer chains?
A. 29 ft
B. 36 ft
C. 42 ft
D. 58 ft
E. 72 ft
Answers
Answer:
29 feet
Step-by-step explanation:
14 × 3 = 42
100 - 42 = 58
58 ÷ 2 = 29
One of the longer chains is 29 feet long.
Hope this helps.
You good at school and I’m finna get a y
Cindy went to the salon to get highlights and a haircut. Her total cost was $95. Cindy decided to tip her stylist 22% because she loved her hair so much. How much was the tip?
Answers
Solve fast and get brainalliest

Answers
Answer:
13 one answer is 212+22−82 pls add me brainliest
Solve |h+3|<5. Write the solution set using set-builder notation.
Answers
Answer:
To solve the inequality |h + 3| < 5, we need to consider two cases, depending on whether the expression inside the absolute value bars is positive or negative:
Case 1: h + 3 >= 0
If h + 3 >= 0, then we can remove the absolute value bars without changing the inequality:
h + 3 < 5
Subtracting 3 from both sides, we get:
h < 2
So the solution for this case is h < 2.
Case 2: h + 3 < 0
If h + 3 < 0, then the inequality becomes:
-(h + 3) < 5
Multiplying both sides by -1 (and reversing the inequality), we get:
h + 3 > -5
Subtracting 3 from both sides, we get:
h > -8
So the solution for this case is h > -8.
Putting these two solutions together, we have:
-8 < h < 2
Therefore, the solution set in set-builder notation is:
{h | -8 < h < 2}