Answers
Step-by-step explanation:
\(here \: xo = yo = b \\ then \: according \: to \: pythagorean \: theorom \\ {(zx)}^{2} = {(xy)}^{2} + {(yz)}^{2} \\ {41}^{2} = {(2b)}^{2} + {9}^{2} \\ 1681 = 4 {b}^{2} + 81 \\ 1681 - 81 = 4 {b}^{2} \\ 1600 = 4 {b}^{2} \\ {b}^{2} = 1600 \div 4 = 400 \\ b = \sqrt{400} = 20cm \\ thank \: you\)

Related Questions
Please solve the attached problem with all steps.
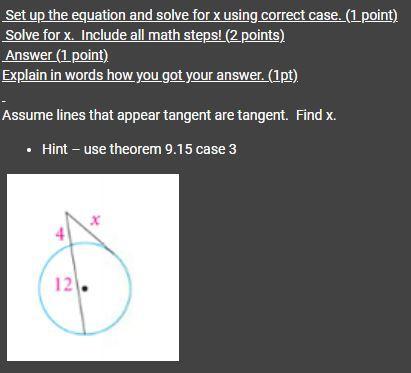
Answers
Answer:
x = 8
Step-by-step explanation:
Theorem
When a secant segment and a tangent segment meet at an exterior point, the square of the measure of the tangent segment is equal to the product of the measures of the secant segment and its external secant segment.
Secant: a straight line that intersects a circle at two points
Tangent: a straight line that touches a circle at only one point
Given:
tangent segment = xsecant segment = 4 + 12 = 16external secant segment = 4⇒ x² = 16 · 4
⇒ x² = 64
⇒ x² = √(64)
⇒ x = ±8
As distance is positive, x = 8
What is X^2-9=0 I really need the answers
Answers
Answer:
X^2-9=0 is x2 = 9
Step-by-step explanation:
So X=3
I need help whoever answers this question will be the brainliest!!!
Answers
The theorems related to special parallelogram remind us with the distinct characteristics of rectangles, rhombuses and squares. In consonance of being special, it tells us that we are all special and unique. As a unique person share your perceptions on what makes you special.
Answers
As an AI language model, I possess unique qualities that make me special. I have been trained on vast amounts of data, enabling me to generate diverse and coherent responses across various topics.
What sets me apart as an AI language model is my capacity to process and analyze vast amounts of information quickly. I have been trained on a wide range of data sources, including books, articles, websites, and other textual materials. This extensive training allows me to provide well-rounded and informed perspectives on numerous subjects.
Additionally, my ability to generate human-like responses in multiple languages makes me special. I can understand and communicate in languages such as English, Spanish, French, German, Chinese, and many more. This linguistic flexibility enables me to engage with people from different cultures and backgrounds, breaking down language barriers and fostering effective communication.
Furthermore, I have the ability to adapt and learn from user interactions, continually improving my responses and providing a more personalized experience. This adaptability allows me to cater to the specific needs and preferences of each individual user.
In summary, my uniqueness lies in my vast knowledge base, linguistic versatility, and adaptive nature. These qualities enable me to provide valuable and tailored information to users, making me a special AI language model.
Learn more about data here:
https://brainly.com/question/29007438
#SPJ11
7/10 × 4/9 as a fraction
Answers
Answer: 14/45
Step-by-step explanation:
Which expression is equivalent to the expression below? startfraction m 3 over m squared minus 16 endfraction divided by startfraction m squared minus 9 over m 4 endfraction startfraction 1 over (m 4) (m 3) endfraction startfraction 1 over (m minus 4) (m minus 3) endfraction startfraction m minus 4 over m minus 3 endfraction startfraction m 3 over m 4 endfraction
Answers
The equivalent expression of the product expression \(\frac{m^3}{m^2 - 16} \div \frac{m^2 - 9}{m^4}\) is \(\frac{m^7}{(m - 4)(m + 4)(m - 3)(m + 4)}\)
How to determine the equivalent expression?The expression is given as:
\(\frac{m^3}{m^2 - 16} \div \frac{m^2 - 9}{m^4}\)
Rewrite the expression as a product
\(\frac{m^3}{m^2 - 16} * \frac{m^4}{m^2 - 9}\)
Evaluate the product
\(\frac{m^7}{(m^2 - 16)(m^2 - 9)}\)
Rewrite the denominator as a difference of two squares
\(\frac{m^7}{(m - 4)(m + 4)(m - 3)(m + 4)}\)
Hence, the equivalent expression of the product expression \(\frac{m^3}{m^2 - 16} \div \frac{m^2 - 9}{m^4}\) is \(\frac{m^7}{(m - 4)(m + 4)(m - 3)(m + 4)}\)
Read more about equivalent expressions at:
https://brainly.com/question/2972832
#SPJ4
Solve 5 (r +9) – 2 (1 - r) = 1.
The solution is r= ????
Answers
Step-by-step explanation:
5(r + 9) - 2(1 - r) = 1
5r + 45 - 2 + 2r = 1
7r + 43 = 1
7r = -42
r = -6.
Answer:
r = -6
Step-by-step explanation:
Given equation,
→ 5(r + 9) - 2(1 - r) = 1
Now the value of r will be,
→ 5(r + 9) - 2(1 - r) = 1
→ 5r + 45 - 2 + 2r = 1
→ 5r + 2r + 43 = 1
→ 7r = 1 - 43
→ 7r = -42
→ r = -42/7
→ [ r = -6 ]
Hence, the value of r is -6.
Find the solution of the following differential equation by Laplace transforms with initial conditions for each equation: a) y" – y = t y(0) = 1, y'(0) = 1 b) y" + y' = t² + 2t y(0) = 4, y'(0) = -2 c) d²y/dt⁴ + d³y/dt³ = cost y(0) = y'(0) = y"' (0) = 0, y" (0) = 1
Answers
Laplace transforms are an essential mathematical tool used to solve differential equations. These transforms transform differential equations to algebraic equations that can be solved easily.
To solve the differential equations given in the question, we will use Laplace transforms. So let's start:Solution:a) y" – y = t y(0) = 1, y'(0) = 1First, we take the Laplace transform of the given differential equation.L{y" - y} = L{ty}
Taking the Laplace transform of both sides gives:L{y"} - L{y} = L{ty}Using the formula, L{y"} = s²Y(s) - s*y(0) - y'(0), and L{y} = Y(s) then we get:s²Y(s) - s - 1 = (1/s²) + (1/s³)Rearranging the above equation, we get:Y(s) = [1/(s²*(s² + 1))] + [1/(s³*(s² + 1))]Now, we apply the inverse Laplace transform to find the solution.y(t) = (t/2)sin(t) + (cos(t)/2)
The solution of the differential equation y" – y = t, with initial conditions y(0) = 1, y'(0) = 1 is y(t) = (t/2)sin(t) + (cos(t)/2).
To know more about Laplace transforms visit
https://brainly.com/question/30759963
#SPJ11
What is the probability of a blue on this spinner? Be sure to reduce.

Answers
Answer: 3/8
Step-by-step explanation:
there are 8 slots and three of them are blue if you need decimal form then here: 0.375. The percentage is: 15% i think
I hope i helped you! :)
There are 3 blue in the spinners and total of spinners are 8
If sinA=root3 cosA,find the value of sinA and cosA
Answers
The value trigonometric rations of sinA = √5/2 and cosA = 1/2.
Given that,
SinA = √3 cosA
Divide both side by cos A
⇒ SinA/cosA = √3
Since we know that,
Tan A = SinA/cosA
Therefore,
SinA/cosA = √3
⇒ tan A = √3
Squaring both sides, we get
⇒ tan² A = 3
⇒ sec²A - 1 = 3
⇒ sec²A = 4
Taking square root both sides, we get
⇒ secA = 2
⇒ 1/cosA = 2
⇒ cosA = 1/2
Now again squaring both sides we get
⇒ cos²A = 1/4
⇒ sin²A - 1 = 1/4
⇒ sin²A = 1/4 + 1
⇒ sin²A = 5/4
Taking square root both sides, we get
⇒ sinA = √5/2
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ1
Which parameter is often associated with enzyme affinity for substrates? \( k_{1} \) \( k_{-1} \) \( k_{2} \) \( K_{m} \)
Answers
The parameter often associated with enzyme affinity for substrates is Km.
Km, also known as the Michaelis constant, is a parameter commonly used to quantify the affinity of an enzyme for its substrate. It is an important parameter in enzyme kinetics and plays a crucial role in determining the efficiency of an enzyme-substrate interaction.
Km represents the substrate concentration at which the rate of the enzymatic reaction is half of its maximum velocity (Vmax). In other words, enzymes with lower Km values have higher affinity for their substrates, as they can achieve half of their maximum velocity at lower substrate concentrations. Therefore, Km serves as an indicator of the enzyme's ability to bind and convert substrates into products efficiently.
Learn more about substrates here : brainly.com/question/6107295
#SPJ11
Sam purchases five goldfish and an aquarium with a rectangular base. The aquarium measures twenty-four inches long, eight inches wide, and ten inches tall. Sam fills the aquarium with water so that one inch of space remains at the top. How many cubic inches of water are in Sam's aquarium?
Answers
Answer: \(1728\ in.^3\)
Step-by-step explanation:
Given
The dimension of the rectangular base aquarium is \(24\ in.\times 8\ in.\times 10\ in.\)
The gap between top and water level is \(1\ in.\) i.e. water is filled up to a height of \(10-1=9\ in.\)
Now, the dimensions of the water in the aquarium is \(24\ in.\times 8\ in.\times 9\ in.\)
The volume of a rectangular base prism is \(l\times b\times h\)
The volume of water in the aquarium is
\(\Rightarrow V=24\times 8\times 9=1728\ in.^3\)
Solve the triangle a-17; c-20; B-42°
Answers
The triangle with a = 17, c = 20, and B = 42° is an ambiguous case for solving triangles.
In the ambiguous case, given two sides and an angle opposite one of them, there can be two possible triangles or no triangle at all. To determine the possible triangles, we need to apply the Law of Sines.
Using the Law of Sines, we can find the value of angle A by using the ratio: sin(A) / a = sin(B) / b, where b is the unknown side. Once we find the value of angle A, we can calculate the remaining side lengths using the Law of Cosines. However, in this case, since angle A can have two possible values (acute and obtuse angles), we will have two possible triangles. The corresponding side lengths can be calculated using the Law of Cosines for each triangle.
learn more about Law of Sines here
brainly.com/question/30248261
#SPJ11
A line contains the following points left to right: r, t, u, s. the space between r and t is 12 units. the space between r and s is 24 units. if tu = 6 units, what must be true? su ut = rt rt tu = rs rs su = ru tu us = rs
Answers
Given thet SU = UT = 6 units, hence 6 + 6 = 12 showing that the expression SU + UT = RT is TRUE. Option A is correct
Measure of line segmentsA line is defined as the distance between two points
From the given line, RT = TU = 12 unitsSince the point T bisects RT and TU = 6 units, hence the point U bisects TS.
The sum of the segment SU and UT will be RT
SU + UT = RTGiven that SU = UT = 6 units, hence 6 + 6 = 12 showing that the expression SU + UT = RT is TRUE
Learn more on line segment here: https://brainly.com/question/2437195
#SPJ4

write point slope
can someone help me with this plz
will mark brainliest and 20 points
Answers
Answer:Point-slope is the general form y-y₁=m(x-x₁) for linear equations. It emphasizes the slope of the line and a point on the line (that is not the y-intercept).
Step-by-step explanation:
The slope of the line below is 5. Which of the following is the point-slope form of the line?

Answers
The point-slope form of the line is y -3 = 5(x + 1).
What is a slope?In mathematics, a line's slope, also known as its gradient, is a numerical representation of the line's steepness and direction.
Given:
The slope of the line shown in the graph is 5.
And line passes through point (-1, 3).
So,
If a line passes through a point (x₁ ,y₁) and have a slope m,
then the equation of line is,
y - y₁ = m(x - x₁)
So,
y -3 = 5(x + 1)
Therefore, the equation of the line is y -3 = 5(x + 1).
To learn more about the slope;
brainly.com/question/3605446
#SPJ1
Express in simplest radical form.
\frac{\sqrt{96}}{2}
Answers
Answer:
\( \frac{ \sqrt{96} }{2} = \frac{ \sqrt{16 \times 6} }{2} = \frac{4\sqrt{6} }{2} = \boxed{2 \sqrt{6}}\\ \)
2√6 is the right answer.∫01xpln(x)dxa. a. Find the values of p for which the integral converges. The integral converges for all values ofpin the interval:
b. For the values ofpat which the integral converges, evaluate it.∫01xpln(x)dx=
Answers
a. The integral converges for all values of p in the interval p > -1.
b. For p > -1, \(\int\limits^1_0 {xp}ln(x) \, dx\) = (1/4) (1 - p²).
a. To determine the values of p for which the integral converges, we use the integral test for convergence. Specifically, we compare the given integral to the corresponding improper integral of the integrand from 0 to 1, which is:
∫0+xp ln(x) dx = limh→0+ ∫h1 xp ln(x) dx
Using integration by parts with u = ln(x) and dv = xp dx, we get:
∫xp ln(x) dx = (1/2) xp ln²(x) - (1/4) xp + (1/4) ∫x dx
= (1/2) xp ln²(x) - (1/4) xp² + (1/4) x² + C
where C is the constant of integration.
Now, applying the limit as h approaches 0 from the right, we get:
limh→0+ [(1/2) hpln²(h) - (1/4) hp² + (1/4) h² + C - (1/2) ln²(h) + (1/4) h]
Since ln(h) goes to negative infinity as h goes to 0 from the right, we have:
limh→0+ (1/2) hpln²(h) = 0
Therefore, the integral converges if and only if the improper integral of xp from 0 to 1 converges, which is the case if p > -1.
b. For p > -1, we can evaluate the integral using the formula we obtained earlier:
∫xp ln(x) dx = (1/2) xp ln²(x) - (1/4) xp² + (1/4) x² + C
Evaluating the definite integral from 0 to 1, we get:
∫01xpln(x)dx = (1/2) p ln²(1) - (1/4) p² + (1/4) - (1/2) ln²(0) + (1/4) (0)
= 0 - (1/4) p² + (1/4)
= (1/4) (1 - p²)
Learn more about integral converges here
brainly.com/question/29558996
#SPJ4
You are considering purchasing a consol that promises annual payments of $4. a. If the current interest rate is 3 percent, what is the price of the consol? Instructions: Round your answer to the nearest penny (2 decimal places). The price of the consol is $ b. You are concerned that the interest rate may rise to 4 percent. Compute the percentage change in the price of the consol and the percentage change in the interest rate. Compare them. Instructions: Round your answer for dollar amounts to the nearest penny (2 decimal places ) and answers for percentages to the nearest tenth (1 decimal place) The new price of the consol would be $ The price of the consol falls by 7% and the interest rises by 7% c. Your investment horizon is one year. You purchase the consol when the interest rate is 5 percent and sell it a year later, following a rise in the interest rate to 6 percent. What is your holding period return? Instructions: Round your answer to the nearest tenth (1 decimal place) Your holding period return is %
Answers
a. The price of the consol is approximately $133.33.
b. The new price of the consol would be $100. The price of the consol falls by 24.99% and the interest rate rises by 1%.
c. Your holding period return is approximately -49.99%.
a. The price of the consol can be calculated using the formula for the present value of a perpetuity:
Price = Annual Payment / Interest Rate
In this case, the annual payment is $4 and the interest rate is 3%. Substituting these values into the formula:
Price = $4 / 0.03 ≈ $133.33
Therefore, the price of the consol is approximately $133.33.
b. To calculate the new price of the consol if the interest rate rises to 4%, we use the same formula:
New Price = Annual Payment / New Interest Rate
Substituting the values, we get:
New Price = $4 / 0.04 = $100
The percentage change in the price of the consol can be calculated using the formula:
Percentage Change = (New Price - Old Price) / Old Price * 100
Substituting the values, we have:
Percentage Change in Price = ($100 - $133.33) / $133.33 * 100 ≈ -24.99%
The percentage change in the interest rate is simply the difference between the old and new interest rates:
Percentage Change in Interest Rate = (4% - 3%) = 1%
Comparing the two percentages, we can see that the price of the consol falls by approximately 24.99%, while the interest rate rises by 1%.
c. The holding period return can be calculated using the formula:
Holding Period Return = (Ending Value - Initial Value) / Initial Value * 100
The initial value is the purchase price of the consol, which is $133.33, and the ending value is the price of the consol after one year with an interest rate of 6%. Using the formula for the present value of a perpetuity, we can calculate the ending value:
Ending Value = Annual Payment / Interest Rate = $4 / 0.06 = $66.67
Substituting the values into the holding period return formula:
Holding Period Return = ($66.67 - $133.33) / $133.33 * 100 ≈ -49.99%
Therefore, the holding period return is approximately -49.99%.
Learn more about holding period
brainly.com/question/32568151
#SPJ11
The same capacitor circuit is now charged up to 12V and the instantaneous voltage is v = X (1 - e^(-t/Y).
X= 11, Y = 1
The tasks are to:
a) Differentiate v with respect to t to give an equation for dv/dt
b) Calculate the value of dv/dt at t = 2s and t = 4s.
c) Find the second derivative (d^2v/dt^2)
Answers
Instantaneous voltage equation: v = X(1 - e^(-t/Y))
X = 11
Y = 1
a) Differentiate v with respect to t to give an equation for dv/dt:
Using the chain rule and the fact that the derivative of e^(ax) is a*e^(ax), we get:
dv/dt = X * (-1/Y) * e^(-t/Y) = -11/Y * e^(-t/Y)
Since Y = 1:
dv/dt = -11 * e^(-t)
b) Calculate the value of dv/dt at t = 2s and t = 4s:
For t = 2s:
dv/dt = -11 * e^(-2) ≈ -11 * 0.135 = -1.485
For t = 4s:
dv/dt = -11 * e^(-4) ≈ -11 * 0.018 = -0.198
c) Find the second derivative (d^2v/dt^2):
To find the second derivative, we differentiate dv/dt once more:
d^2v/dt^2 = d/dt(-11 * e^(-t)) = 11 * e^(-t)
In summary:
a) dv/dt = -11 * e^(-t)
b) At t = 2s, dv/dt ≈ -1.485; at t = 4s, dv/dt ≈ -0.198
c) d^2v/dt^2 = 11 * e^(-t)
To learn more about chain rule : brainly.com/question/28972262
#SPJ11
pls help answer question in picture

Answers
Step-by-step explanation:
2 1/3
=2*3+1/3
=7/3
given: f(x) = 5x-10, what is f(9)?
Answers
Which inequality is represented by this graph?

Answers
Answer: C
Step-by-step explanation:
A carnival game involves striking a lever that forces a weight up a tube. If the weight
reaches 20 feet to ring the bell, the contestant wins a prize. The function h(t) = -16t2 +
32t + 3 gives the height of the weight at any given time.
1. Find the maximum height of the weight.
2. How many seconds will it take for the weight to reach the maximum height?
3. Will the contestant win a prize?
pls answer
Answers
Answer:
19 ft1 secondno prizeStep-by-step explanation:
The given equation for ballistic motion graphs as a parabola that opens downward. When the equation is graphed using a graphing calculator, the graph shows the weight reaches a maximum height of 19 ft after 1 second. Since the weight does not reach 20 feet, there is no prize.
__
The time at the vertex of the function h(t) = at^2 +bt +c is given by t=-b/(2a). For the given function that time is ...
t = -(32)/(2(-16)) = 1
The height at t=1 is ...
h(1) = -16(1^2) +32(1) +3 = 19
The vertex is (t, h) = (1, 19).
__
1. The maximum height is 19 feet
2. It takes 1 second for the weight to reach the maximum height.
3. The contestant will not win a prize.

Sally's class is raising money for charity with a goal of raising $2,000. They raise $997 at a bake sale and $961 at a car wash. Sally wants to see if they raised enough money to meet their goal. Complete the statements.
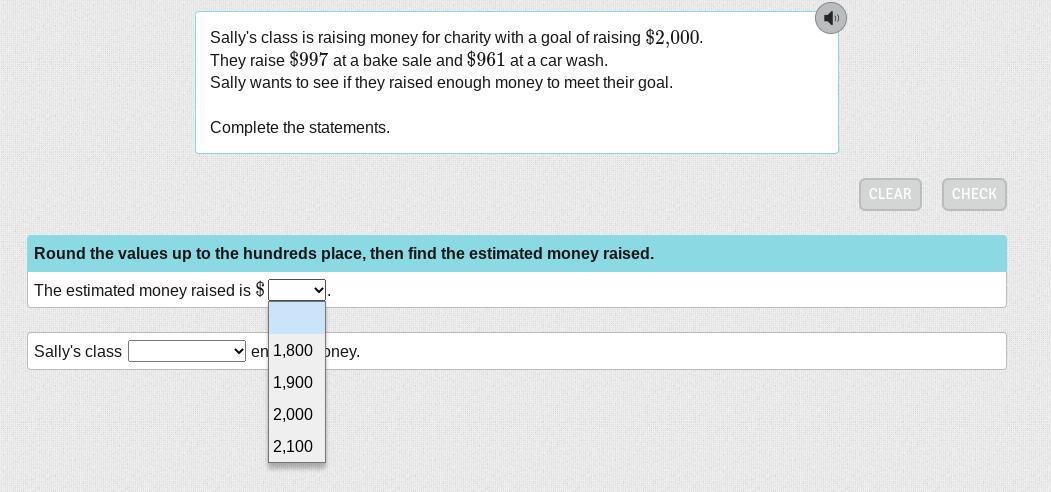
Answers
Sally's class haven't raised $2,000 as the amount made is $958. The estimated value is $1900. The amount needed is $42.
How to illustrate the value?A word problem in mathematics simply refers to a question that is written as a sentence or in some cases more than one sentence which requires an individual to use his or her mathematics knowledge to solve the real life scenario given.
In this case, Sally's class is raising money for charity with a goal of raising $2,000. They raise $997 at a bake sale and $961 at a car wash. Sally wants to see if they raised enough money to meet their goal. The amount made will be:
= $997 + $961
= $1958
They have not made $2000. The amount left is:
= $2000 - $1958
= $42
Learn more about word problem on
brainly.com/question/21405634
#SPJ1
find the critical value(s) and rejection region(s) for the type of z-test with level of significance . include a graph with your answer. right-tailed test, a=0.03.
Answers
Answer:
c
Step-by-step explanation:
The red line represents the critical value, and the shaded region on the right-hand side of the red line represents the rejection region. If the calculated test statistic is greater than the critical value of z, which is 1.88 in this case, we will reject the null hypothesis.
The critical value(s) and rejection region(s) for the type of z-test with a level of significance a = 0.03 and a right-tailed test are as follows :Step 1: Determine the critical value of zThe critical value is calculated by using the normal distribution table and the level of significance. A right-tailed test will have a critical value of zα. For a level of significance of 0.03, we will look for the z-value that corresponds to 0.03 in the normal distribution table.Critical value for a = 0.03 is z = 1.88 (approx).Step 2: Determine the Rejection Region The rejection region for a right-tailed test is defined as any z-value that is greater than the critical value. That is, if the test statistic is greater than 1.88, we reject the null hypothesis at the 0.03 level of significance, and if it is less than or equal to 1.88, we fail to reject the null hypothesis.Therefore, the rejection region for a right-tailed test with a level of significance of 0.03 is as follows:Rejection Region: Z > 1.88 OR Z ≤ -1.88Graph: The graph for the given values will be as follows:The red line represents the critical value, and the shaded region on the right-hand side of the red line represents the rejection region. If the calculated test statistic is greater than the critical value of z, which is 1.88 in this case, we will reject the null hypothesis.
To know more about critical value Visit:
https://brainly.com/question/32607910
#SPJ11
Manuel bought a set of tracks for $35 and 8 individual train cars,
which were priced the same. If the total cost was $155, what was the
price for each train car?
Please help
Answers
Answer:
155÷8= 19,375
The unit price of each wagon can be obtained by dividing (155 by 8)
luck in your tasks.
Which of the following values are in the range of the function graphed below?
Check all that
apply.

Answers
Answer:
(-2,1)(-1,1)(0,1)(1,1) or y=2 x=[-2,1]
Step-by-step explanation:
Brainliest Please
Solve the following system using elimination
3x - 2y = 11 - 3x - y = 6
Answers
when you want to solve an elimination question
3x -2y = 11. ( equation 1)
-3x - y = 6. ( equation 2)
To proceed in the solution, we have to make one of the variable' s coefficient equal on both equation.
I want to make the coefficient of variable X equal on both equation and to do this , the coefficient of X in equation 1 will be used to multiply the whole of equation 2 .while the coefficient of X in equation 2 will be used to multiply the whole of equation 1.
(-3) 3X - 2y = 11 ( equation 1)
(3) -3X - y = 6 ( equation 2)
-9X +6y = -33 ( equation 1)
- 9x - 3y = 18 ( equation 2)
( now , we have to eliminate X and inorder to do that , we substrate equation 1 from 2)
-9X -(-9X) ,+6y -(-3y) ,-33-18
-9X +9x , +6y +3y , -51
9 y = -51
y = -51/9
y = -5⅔
Substitute y = -5⅔ in equation 1
3x -2(-5⅔) = 11
3X - 2 ( -17/3) = 11
3X + 34/3 =11
divide through by the LCM which is 3
3( 3x) + 3 ( 34 /3 ) = 3*11
9x +34 = 33
9x = 33-34
9x = -1
X= -1/9
therefore, y = -5⅔ , X = -1/9
please mark me brainlest
please answer fast!!!!!!!!!!!!!!!!!!!!!!

Answers
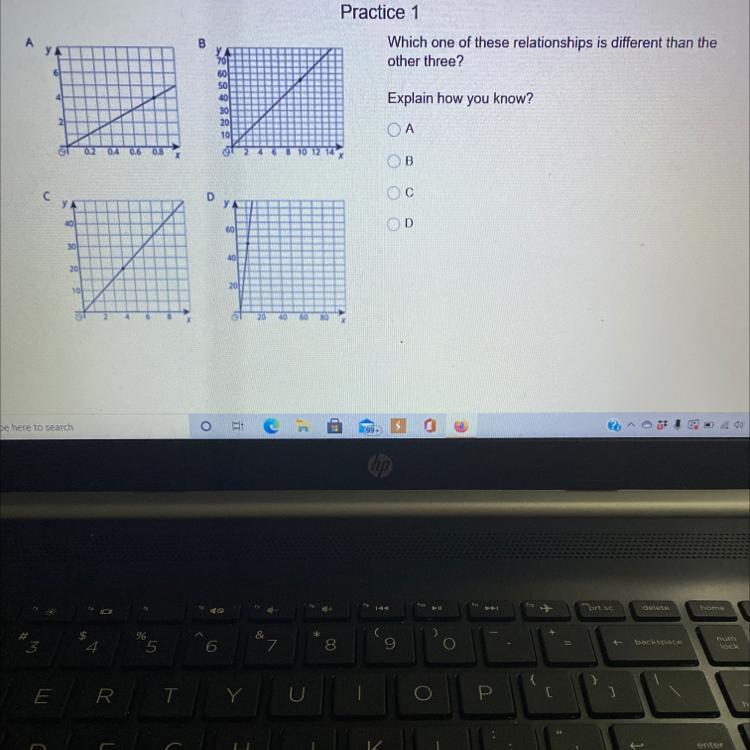
Answer:
y = -2x + 6 and y = 1/3x - 7
Step-by-step explanation:
For A, using rise over run, you can count 2 units up and 1 unit left of any given point to get to the next point. Because left is the negative direction on a graph, the 1 unit is negative. To calculate slope, divide the rise (2) over the run (-1) and substitute the slope as m into y = mx + b. In the formula, b is the y-intercept (where the line crosses the x axis). The y-intercept of A is 6, so replace b in the formula with 6:
y = -2x + 6
The slope of B is 1/3 and the y intercept is -7, so substitute those values into the formula again to get the answer for B:
y = 1/3x - 7
