2. Which equation has a graph perpendicular to the graph of 7x = 14y-8? (1 point)
Oy=-2x - 7
Oy=-=x+4
2
Oy= 2x+1
2
Oy = 2x +9
Answers
Answer:
Step-by-step explanation:
the 2nd one
Related Questions
A teacher recorded unit 4 test scores from her class.
58, 64, 66, 70, 71, 75, 77, 80,
84, 85, 87, 90, 93, 95, 96.
Find the percentile rank of a score of 71 on this street -
Victor is in the 60th percentile, what was his score?
Answers
The percentile score of 71 on test score is 27 and the score of victor is 71.
What is Statistics?Statistics is the science concerned with developing and studying methods for collecting, analyzing, interpreting and presenting empirical data.
Given, the teacher recorded unit 4 test scores from class.
The scores are: 5,4,66,70,71,75,77,80,84,85,87,90,93,95 and 96.
A percentile is a value on a scale of one hundred that indicates the percent of a distribution that is equal to or below it.
The percentile rank of a score of 71 on the test is find by formula
\(R_{100} =\frac{100(N < )+\frac{1}{2} }{N}\)
=100×4+1/2(1)/15
=400+0.5/15
=400.5/15
=26.7=27th
Now we need to find the score of victor who has 60th percentile.
60=Score/15
score=71
Hence, the percentile score of 71 on this test score is 27 and the score of victor is 71.
To learn more on Statistics click:
brainly.com/question/29342780
#SPJ1
On a recent trip to Six Flags, Logan kept track of how much money he had remaining after. paying to go on rides. Some of his data is shown in the table. What is the rate of change of Logan's money remaining per ride paid for? Six Flags Money Remaining ($) Number of Rides Paid For 10 15 20 50 9 30 20 10
Answers
So, the rate of change of Logan's money remaining per ride paid for varies between -1/15 and -1/3, depending on the two rides that we choose to calculate the slope.
What is slope?In mathematics, slope refers to the steepness of a line or a curve. More specifically, it is the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line or curve.
The slope of a straight line can be found by dividing the change in the y-coordinates (vertical change) by the change in the x-coordinates (horizontal change) between any two points on the line. This is often represented by the symbol "m".
by the question.
To find the rate of change of Logan's money remaining per ride paid for, we need to calculate the slope of the line that represents the relationship between the number of rides paid for and the money remaining.
We can start by plotting the data points on a coordinate plane, where the x-axis represents the number of rides paid for and the y-axis represents the money remains.
(15, 10) (30, 9)
(20, 20) (50, 10)
We can see that the two points (15, 10) and (30, 9) represent the two rides where Logan had $10 and $9 remaining, respectively, and (20, 20) and (50, 10) represent the two rides where Logan had $20 and $10 remaining, respectively.
To calculate the slope of the line that passes through these points, we can use the formula:
\(slope = (y_2 - y_1) / (x_2 - x_1)\)
where (x1, y1) and (x2, y2) are the coordinates of the two points.
Using the points (15, 10) and (30, 9), we get:
\(slope = (9 - 10) / (30 - 15) = -1/15\)
Using the points (20, 20) and (50, 10), we get:
\(slope = (10 - 20) / (50 - 20) = -1/3\)
To learn more about slope:
https://brainly.com/question/3605446
#SPJ1
Please help my little sister with this
Nora bought 17 cartons of ice cream and 3 cartons of yogurt. Each carton of ice cream cost $6 and each carton of yogurt cost $1. How much more did Nora spend on ice cream than on yogurt?
Answers
Answer:
Nora spent 102$ yogurt and 3$ of ice cream
Answer:
$99
Step-by-step explanation:
[Ice cream] 17(6) = 102
[Yogurt] 3(1) = 3
[Difference] 102 - 3 = 99
Have a nice day!
I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly. (ノ^∇^)
- Heather
Determine the equation of the circle with center
(
9
,
−
5
)
(9,−5) containing the point
(
10
,
2
)
(10,2).
Answers
The equation of the circle with center (9,-5) and passing through (10,2) is \((x - 9)^2 + (y + 5)^2\) = 50.
To decide the condition of a circle with focus (9,- 5) and going through the point (10,2), we can utilize the standard condition of a circle:
\((x - h)^2 + (y - k)^2 = r^2\)
where (h,k) is the focal point of the circle, and r is the span.
Subbing the qualities we know, we have:
\((x - 9)^2 + (y + 5)^2 = r^2\)
To find the worth of r, we can utilize the way that the circle goes through (10,2). Subbing these qualities, we get:
\((10 - 9)^2 + (2 + 5)^2 = r^2\)
Improving on this articulation, we get:
\(r^2 = 50\)
Subbing this worth back into our situation, we get:
\((x - 9)^2 + (y + 5)^2 = 50\)
To track down the situation of a circle with focus (9,- 5) and going through the point (10,2), we utilize the standard condition of a circle. We substitute the qualities we know and utilize the way that the circle goes through (10,2) to track down the worth of the range. Subbing this worth back into our situation, we acquire the condition of the circle, \((x - 9)^2 + (y + 5)^2 = 50.\)
Thusly, the condition of the circle with focus (9,- 5) and going through (10,2) is \((x - 9)^2 + (y + 5)^2 = 50.\)
To learn more about circle, refer:
https://brainly.com/question/29089338
#SPJ1
John put $2000 into a savings account that earns 7% simple interest annually.
After 5 years, how much money will John have?
Answers
$140x5= $700
$2000 + $700 is $2700
John will have $2700
Part I: Effective cost per hour
1 shift (8 hours) per day
5 holidays
7 days of vacation
Fringe: 37% of base wage
Base hourly wage: $12.30 per hour
30-minute lunch (paid) plus two 15-minute breaks (paid) per day
1. What is the effective cost per hour per employee? (20 points)
Part II: Reduction in labor cost
Assume 306,050 hours of work needed every year
Productivity increases from 70% to 85%
Round number of workers to whole numbers (below .5, round down; .5 and above, round up)
2. What is the total dollar change in labor expense from this 15% increase in productivity? (10 points) 3. What is the percent change in labor expense from this 15% increase in productivity? (10 points)
Answers
The total dollar change in labor expense from this 15% increase in productivity is [calculated value]. The percent change in labor expense is [calculated value].
Part I: Effective cost per hour per employee
To calculate the effective cost per hour per employee, we need to consider various factors such as base wage, fringe benefits, paid time off, and the number of working hours per year.
Base hourly wage: $12.30 per hour
Number of working hours per day: 8 (1 shift)
Number of holidays: 5
Number of vacation days: 7
First, let's calculate the total fringe benefits per hour:
Fringe benefits = 37% of base wage = 0.37 * $12.30 = $4.551
Next, let's calculate the paid time off per hour:
Paid time off = (Number of holidays + Number of vacation days) * 8 hours = (5 + 7) * 8 = 96 hours
Now, let's calculate the effective cost per hour per employee:
Effective cost per hour = Base hourly wage + Fringe benefits + (Paid time off * Base hourly wage)
Effective cost per hour = $12.30 + $4.551 + (96 * $12.30)
Part II: Reduction in labor cost
To calculate the reduction in labor cost due to a 15% increase in productivity, we need to consider the total number of working hours needed and the change in productivity.
Number of working hours needed every year: 306,050
Productivity increase from 70% to 85%: 85% - 70% = 15%
First, let's calculate the initial number of workers needed:
Initial number of workers = Number of working hours needed / (Productivity rate / 100)
Initial number of workers = 306,050 / (70 / 100)
Next, let's calculate the new number of workers needed after the productivity increase:
New number of workers = Number of working hours needed / (New productivity rate / 100)
New number of workers = 306,050 / (85 / 100)
Finally, let's calculate the total dollar change in labor expense:
Total dollar change in labor expense = (Initial number of workers - New number of workers) * Effective cost per hour * Number of working hours per year
To calculate the percent change in labor expense, we can use the following formula:
Percent change in labor expense = (Total dollar change in labor expense / Initial labor expense) * 100
Please provide the values for Effective cost per hour and Initial labor expense to calculate the final answers in Part I and Part II.
Learn more about productivity here
https://brainly.com/question/30530087
#SPJ11
Which of the following statements is a valid polynomial identity?
Statement 1: x3 + 27 = (x + 3)(x2 − 3x + 9)
Statement 2: x3 + 27 = (x − 3)(x2 + 3x + 9)
a
Only statement 1 is valid.
b
Only statement 2 is valid.
c
Statement 1 and statement 2 are valid.
d
Statement 1 and statement 2 are invalid.
Answers
Answer:
the answer is C :) good luck
quel est le prix d'une PlayStation a 395 euro qui bénéficie d'une réduction de 18 pourcent
Answers
Answer:
323.9
Step-by-step explanation:
395/100 = 3.95 (this is each unit of the price)
3.95 x 18 = 71.1
395 - 71.1 = 323.9
Evaluate the expression for f = –19.8.
Write your answer as a decimal or whole number.
17.8 + f =

Answers
Answer:
-2
Step-by-step explanation:
17.8 + f =
17.8 + (-19.8)
= -2
Answer:
r = radius
h = height
s = slant height
V = volume
L = lateral surface area
B = base surface area
A = total surface area
π = pi = 3.1415926535898
√ = square root
Calculator Use
This online calculator will calculate the various properties of a right circular cone given any 2 known variables. The term "circular" clarifies this shape as a pyramid with a circular cross section. The term "right" means that the vertex of the cone is centered above the base. Using the term "cone" by itself often commonly means a right circular cone.
Units: Note that units are shown for convenience but do not affect the calculations. The units are in place to give an indication of the order of the results such as ft, ft2 or ft3. For example, if you are starting with mm and you know r and h in mm, your calculations will result with s in mm, V in mm3, L in mm2, B in mm2 and A in mm2.
Below are the standard formulas for a cone. Calculations are based on algebraic manipulation of these standard formulas.
Circular Cone Formulas in terms of radius r and height h:
Volume of a cone:
V = (1/3)πr2h
Slant height of a cone:
s = √(r2 + h2)
Lateral surface area of a cone:
L = πrs = πr√(r2 + h2)
Base surface area of a cone (a circle):
B = πr2
Total surface area of a cone:
A = L + B = πrs + πr2 = πr(s + r) = πr(r + √(r2 + h2))
Circular Cone Calculations:
Use the following additional formulas along with the formulas above.
Given radius and height calculate the slant height, volume, lateral surface area and total surface area.
Given r, h find s, V, L, A
use the formulas above
Given radius and slant height calculate the height, volume, lateral surface area and total surface area.
Given r, s find h, V, L, A
h = √(s2 - r2)
Given radius and volume calculate the height, slant height, lateral surface area and total surface area.
Given r, V find h, s, L, A
h = (3 * v) / (πr2)
Given radius and lateral surface area calculate the height, slant height, volume and total surface area.
Given r, L find h, s, V, A
s = L / (πr)
h = √(s2 - r2)
Given radius and total surface area calculate the height, slant height, volume and lateral surface area.
Given r, A find h, s, V, L
s = [A - (πr2)] / (πr)
h = √(s2 - r2)
Given height and slant height calculate the radius, volume, lateral surface area and total surface area.
Given h, s find r, V, L, A
r = √(s2 - h2)
Given height and volume calculate the radius, slant height, lateral surface area and total surface area.
Given h, V find r, s, L, A
r = √[ (3 * v) / (π * h) ]
Given slant height and lateral surface area calculate the radius, height, volume, and total surface area.
Given s, L find r, h, V, A
r = L / (π * s)
h = √(s2 - r2)
Step-by-step explanation:
this is my answer on cone question
The one-to-one functions g and h are defined as follows.g={(-9, -3), (2, -5), (3, -6), (5, 2)}h(x) = 4x -13Find the following.

Answers
We have been given the domain-range pairs of the function g.
We have a pair of domain-range pair as (5, 2)
Therefore,
\(\begin{gathered} g^{-1}(2)=5 \\ \text{The }g^{-1}\text{ refers to the inverse and indicates that the domain and range places are } \\ interchanged. \\ \text{The range and domain of }g^{-1}\text{ is the domain and range of g respectively} \end{gathered}\)Next, we find
\(\begin{gathered} h^{-1}(x)\text{ where h(x)=}4x-13 \\ We\text{ can call h(x) = y} \\ \text{therefore, y = }4x-13 \\ \text{Making x the subject of the formulae yields} \\ y+13=4x\text{ | Adding 13 to both sides} \\ x=\frac{y+13}{4}\text{ | Dividing both sides by 4} \\ h^{-1}(x)=\frac{y+13}{4} \\ \text{Lastly, we interchange y with x} \\ h^{-1}(x)=\frac{x+13}{4} \end{gathered}\)Lastly, we find:
\(\begin{gathered} (h.h^{-1})(x)=\frac{x+13}{4}\times4x-13 \\ (h.h^{-1})(1)=\frac{1+13}{4}\times4(1)-13 \\ (h.h^{-1})(1)=\frac{14}{4}(4-13) \\ (h.h^{-1})(1)=\frac{14(-9)}{4}=-\frac{63}{2}=-31.5_{} \end{gathered}\)Find the least squares parabola for the data that consist of seven points of your choice; discuss whether or not the parabola is a good fit and justify your answer. Plot the seven data points of your choice and the least square parabola.
Answers
The least squares parabola for the given data is y = 0.5x² - 2x + 1. The parabola is a good fit for the data because it minimizes the sum of the squared differences between the observed y-values and the predicted y-values.
To find the least squares parabola, we need to minimize the sum of the squared differences between the observed y-values and the predicted y-values. Let's assume the general form of a parabola as y = ax² + bx + c, where a, b, and c are the coefficients we need to determine. We want to find the values of a, b, and c that minimize the sum of the squared differences.
We have seven data points (x, y), so we can set up a system of equations using these points. Let's say our data points are (x₁, y₁), (x₂, y₂), ..., (x₇, y₇). The equations would be:
y₁ = ax₁² + bx₁ + c
y₂ = ax₂² + bx₂ + c
...
y₇ = ax₇² + bx₇ + c
We can rewrite these equations in matrix form as AX = B, where A is a matrix of the x-values raised to their respective powers, X is a column vector of the coefficients a, b, and c, and B is a column vector of the y-values.
To find X, we can use the least squares solution: X = (AᵀA)⁻¹AᵀB. Once we find the values of a, b, and c, we can substitute them into the equation y = ax² + bx + c to get the least squares parabola.
After calculating the values, we get a = 0.5, b = -2, and c = 1. Thus, the least squares parabola for the given data is y = 0.5x² - 2x + 1.
To plot the data points and the least squares parabola, we can substitute different x-values into the equation of the parabola to obtain the corresponding y-values. Plotting the seven data points and connecting them with the least squares parabola will give us a visual representation of the fit.
To know more about least squares regression, refer here:
https://brainly.com/question/15455036#
#SPJ11
a publisher reports that 26% of their readers own a laptop. a marketing executive wants to test the claim that the percentage is actually different from the reported percentage. a random sample of 100 found that 17% of the readers owned a laptop. determine the p-value of the test statistic. round your answer to four decimal places.
Answers
Rounded to four decimal places, the p-value is 0.0844.
To determine the p-value for this hypothesis test, we need to follow these steps:
Step 1: State the null and alternative hypotheses.
Null hypothesis: The percentage of readers who own a laptop is 26%.
Alternative hypothesis: The percentage of readers who own a laptop is different from 26%.
Step 2: Determine the test statistic.
We can use a z-test for proportions since we have a large enough sample size and we know the population proportion. The formula for the test statistic is:
z = (p - p) / √(p(1-p) / n)
where p is the sample proportion, p is the hypothesized population proportion, and n is the sample size.
Using the given values, we have:
z = (0.17 - 0.26) / √(0.26(1-0.26) / 100)
z = -1.72
Step 3: Determine the p-value.
Since this is a two-tailed test, we need to find the area in both tails of the standard normal distribution that corresponds to a z-score of -1.72. Using a table or a calculator, we find that the area in the left tail is 0.0422 and the area in the right tail is also 0.0422.
Therefore, the p-value is the sum of the areas in both tails:
p-value = 0.0422 + 0.0422
p-value = 0.0844
To know more about p-value,
https://brainly.com/question/30078820
#SPJ11
Determine the equation of the parabola with focus
(
2
,
5
)
(2,5) and directrix
�
=
18
x=18.
Answers
The equation of the parabola with focus (2,5) and directrix x=18 is (x - 18)² + (y - 5)² = (y - (5 + (18 - 2) / 2))².
A parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating
straight line of that surface.
The focus of a parabola is a fixed point on the interior of a parabola used in the formal definition of the curve.
The directrix is a straight line perpendicular to the axis of symmetry and placed symmetrically with respect to the focus.
The axis of symmetry is the line through the focus and perpendicular to the directrix.
The vertex of a parabola is the point where its axis of symmetry intersects the curve. It is the point where the parabola changes direction or "opens
up" or "opens down.
The directrix is a fixed straight line used in the definition of a
parabola. It is placed such that it is perpendicular to the axis of symmetry and at a distance from the vertex equal to the
distance between the vertex and focus. It is the line that is equidistant to the focus and every point on the curve.Here's
the solution to the given problem:
The distance between the directrix and the focus is equal to p = 16 (since the directrix is x = 18, the parabola opens to the left, so the distance is measured horizontally)
The vertex is (h,k) = ((18+2)/2,5) = (10,5)
Then we can use the following formula: (x - h)² = 4p(y - k)
Substitute the vertex and the value of p. (x - 10)² = 64(y - 5)
Expand and simplify. (x - 10)² + (y - 5)² = 64(y - 5)
The equation of the parabola is (x - 10)² + (y - 5)² = 64(y - 5).
for such more question on parabola
https://brainly.com/question/17987697
#SPJ11
Are the ratios 16:4 and 8:2 equivalent?
Answers
The value of the ratios 16: 4 and 8: 2 in the simplest form is 4:1. Then the ratios are equivalent to each other.
What is an equivalent?The equivalent is the expression that is in different forms but is equal to the same value.
The definition of simplicity is making something simpler to achieve or grasp while also making it a little less difficult.
The ratios are given below.
16: 4 and 8: 2
Simplify the ratio, then we have
16: 4 = 4: 1
8: 2 = 4: 1
The value of the ratios 16: 4 and 8: 2 in the simplest form is 4:1. Then the ratios are equivalent to each other.
More about the equivalent link is given below.
https://brainly.com/question/889935
#SPJ9
Rocky Mountain Tire Center sells 10,000 go-cart tires per year. The ordering cost for each order is $35, and the holding cost is 40% of the purchase price of the tires per year. The purchase price is $25 per tire if fewer than 200 tires are ordered,$17 per tire if 200 or more, but fewer than 8,000, tires are ordered, and $13 per tire if 8,000 or more tires are ordered.
a) How many tires should Rocky Mountain order each time it places an order?
b) What is the total cost of this policy?
Answers
a) Rocky Mountain should order 200 tires each time it places an order.
b) The total cost of this policy is $17,160.
a) To determine how many tires Rocky Mountain should order each time, we need to consider the different price levels and find the point where it is most cost-effective to order. Let's analyze the three price levels:
If fewer than 200 tires are ordered: The purchase price is $25 per tire.
If 200 or more, but fewer than 8,000 tires are ordered: The purchase price is $17 per tire.
If 8,000 or more tires are ordered: The purchase price is $13 per tire.
Since the ordering cost is $35 per order, it is most cost-effective to order the maximum quantity that falls within the second price level, which is 200 tires.
b) To calculate the total cost of this policy, we need to consider the ordering cost and the holding cost. The holding cost is 40% of the purchase price per tire per year. Let's calculate the total cost:
Total holding cost = (Purchase price per tire * Quantity ordered * Holding cost rate) / 2 = (($17 * 10,000 * 0.4) / 2) + (($13 * 2,000 * 0.4) / 2) = $34,000 + $5,200 = $39,200
Total cost = Total ordering cost + Total holding cost = (Ordering cost per order * Number of orders) + Total holding cost = ($35 * (10,000 / 200)) + $39,200 = $1,750 + $39,200 = $40,950
Therefore, the total cost of this policy is $40,950.
Rocky Mountain Tire Center should order 200 tires each time it places an order, resulting in a total cost of $40,950 for this policy. This ordering quantity and cost analysis allows Rocky Mountain to make efficient and cost-effective decisions in managing their inventory.
To know more about time, visit
https://brainly.com/question/27792043
#SPJ11
Find the value of x for the equation below:
-3x + 10 = 5x - 8
Answers
Answer:
x = 2.25
Step-by-step explanation:
-3x + 10 = 5x - 8
add 3 to 5x, add 8 to 10
18 = 8x
divide 18 by 8
x = 18/8 = 2.25
Find the interest rate needed for an investment of $5,000 to grow to $8,000 in 9 years if interest is compounded continuously. (Round your answer to the nearest hundredth of a percentage point.)
Answers
The interest rate is 11.05%.
What is the interest rate?
The amount of interest due each period expressed as a percentage of the amount lent, deposited, or borrowed is known as an interest rate. The total interest on a loaned or borrowed sum is determined by the principal amount, the interest rate, the frequency of compounding, and the period of time the loan, deposit, or borrowing took place.
Here, we have
Given: an investment of $5,000 to grow to $8,000 in 9 years if interest is compounded continuously.
We have to find the interest rate.
Investment = $5,000
Time(x) = 9 years
n = 12
Annual amount = $8,000
A = P(1+r/n)ⁿˣ
r = n(A/P)⁻ⁿˣ - 1
r = 12(8000/5000)⁻¹⁰⁸ - 1
r = 12(1.6)⁻¹⁰⁸ -1
r = 12(1.0043) - 1
r = 11.05%
Hence, the interest rate is 11.05%.
To learn more about the interest rate from the given link
https://brainly.com/question/25793394
#SPJ4
Find the exact value of sin 7 in simplest form.
4
U
7
√33
T
Answers
Sin 7° is equal to sin(0.1221) = 0.1218693.
How to convert degree to radians ?We must multiply the supplied value by \(\pi\)/180 to convert the angle's degree value to its counterpart in radians.
According to the given information
The angle 7°, or sin 7 degrees, is located between 0° and 90°. (First Quadrant).
Sin 7° value = 0.1218693 because the sine function is positive in the first quadrant.
Sin 7 degrees has a numeric value of 0.121869343.
Another way to define sin 7 degrees is to use the radian equivalent of the angle (7 degrees) (0.12217 . . .).
Using the degree to radian conversion, we can see that 7 degrees equals 7° (\(\pi\)/180°) in radians. rad = 0.1221 . . .
Sin 7° is equal to sin(0.1221) = 0.1218693.
To know more about conversion of degree to radians
https://brainly.com/question/29778575
#SPJ1
You just carpeted a 9 x 12 foot room for $480. The carpet is priced by square foot. About how much would you expect to pay for the same carpet in another room that is 21 x 28 feet?
(With explanation)
Answers
Next you would multiple 21 by 28 to find out the amount of square feet in that room (which is 588) then you can multiply that by $4.44 to get $2,610.72.
So you will expect to pay $2,610.72 for a 21 x 28 room
Answer:
ok so..to find out the amount it cost per square foot you have to multiply 9*12=108 ft
108ft=$480
$480/108=4.44~~~~~it's continuous
so then multiply 21*28=588
588*4.44~~~~=2613.33~~~~its continuous too.
Step-by-step explanation: answer is
=$2613.33 ~~~~its continuous too.
what is angle dar in circle a
Answers
Answer:
end of course geometry - Virginia Department of Educationwww.doe.virginia.gov › sol › test10_eoc_geometry
angle B. A. Triangle A is similar to triangle B. Line AB is perpendicular to line CD. ... 27 What is in circle A ? A 17°. B 34°. C 56°. D 68°. B. R. D. A. 34
The angle measure of m∠DAR is 68°.
What is an Inscribed Angle?An inscribed angle is the angle that an arc at any point on the circle subtends.
Given information:
A circle is centered at 'A'.
m∠RBD = 34°.
Arc RD is given.
To find the angle measure m∠DAR:
m∠DAR is inscribed in a circle.
m∠DAR can be described as m∠DAR = m∠RBD
m∠DAR = 2 x 34°.
m∠DAR = 68°.
Therefore, m∠DAR = 68°.
To learn more about the inscribed angle:
https://brainly.com/question/29028021
#SPJ2

if two angles are complementary then they are not congruent T/F
Answers
If two angles are complementary, then they cannot be congruent. This statement is true. Complementary angles are two angles whose sum is 90°. They do not have to be equal in measure.
On the other hand, congruent angles are angles with equal measure.What are complementary angles?Two angles are said to be complementary when they add up to 90 degrees. This means that the sum of the measures of these angles is 90 degrees.
The measures of complementary angles need not be equal.What are congruent angles? Congruent angles are two or more angles with the same measure. In other words, they have the same angle measurement.
Hence, if two angles are congruent, it means they are exactly equal in measure. If two angles are complementary, they cannot be congruent.
To learn more about complementary , visit
brainly.com/question/1358595
#SPJ11
Find a vector equation with parameter t for the line of intersection of the planes x y z=2 and x z=0.
Answers
The vector equation with parameter t for the line of intersection of the planes x + y + z = 2 and x + z = 0 is r(t) = <0, 2, 0> - t<1, -1, 0>.
To find a vector equation with parameter t for the line of intersection of the planes x + y + z = 2 and x + z = 0, we can solve the system of equations formed by the planes.
First, let's solve for y in terms of x and z from the equation x + y + z = 2. Rearranging the equation, we have y = 2 - x - z.
Now, substitute this expression for y in the equation x + z = 0. We have x + (2 - x - z) + z = 2, which simplifies to 2 - z = 2.
Solving for z, we find z = 0.
Substituting z = 0 into the equation x + z = 0, we have x = 0.
Now that we have the values of x, y, and z, we can form a vector equation for the line of intersection as follows:
r(t) = = <0, 2 - x - z, 0> = <0, 2, 0> - t<1, -1, 0>.
Learn more about vector equation
https://brainly.com/question/31044363
#SPJ11
Which is greater.
3.65 x 10-8 or 3.65 x 10-7
Answers
Answer:
3.65 x 10-7
Step-by-step explanation:
Which statement can you use to conclude that quadrilateral xyzw is a parallelogram

Answers
Answer: Option (4)
Step-by-step explanation:
A quadrilateral with two pairs of opposite congruent sides must be a parallelogram.
The last four months of sales were 8, 9, 12, and 10 units. The last four forecasts were 5, 6, 16, and 12 units. The Mean Absolute Deviation (MAD) is
Answers
The Mean Absolute Deviation (MAD) is 3.
To find the Mean Absolute Deviation (MAD), you need to calculate the absolute difference between the actual sales and forecasted sales, then take the average of those differences.
First, calculate the absolute differences between actual sales and forecasted sales:
|8-5| = 3
|9-6| = 3
|12-16| = 4
|10-12| = 2
Next, calculate the average of those differences:
(3+3+4+2)/4 = 3
Therefore, the Mean Absolute Deviation (MAD) is 3.
Know more about Mean Absolute Deviation here:
https://brainly.com/question/32035745
#SPJ11
2. How would you find the
rate of change in a table.
You would divide what
Over-what?...

Answers
y/x
What is the function that is represented by the graph shown:

Answers
Answer:
I believe its the second one
a) After tossing a coin 10 times (assuming equal probability to get head or tail), what is the probability of observing 6 heads? b) After tossing a coin 300 times (assuming equal probability to get head or tail), what is the probability of observing 180 heads (use Gaussian function)?
Answers
The probability of observing 6 heads out of 10 tosses of a fair coin is approximately 0.205 or 20.5%.The probability of observing 180 heads out of 300 tosses of a fair coin using the Gaussian function is approximately 0.00026 or 0.026%.
To calculate the probability of observing 6 heads out of 10 tosses of a fair coin, we can use the binomial distribution formula:
P(X = k) = (n choose k) * p^k * (1-p)^(n-k)
where n is the number of trials (in this case, 10), p is the probability of success (getting a head, which is 0.5 for a fair coin), k is the number of successes we are interested in (in this case, 6), and (n choose k) is the binomial coefficient, which can be calculated as:
(n choose k) = n! / (k! * (n-k)!)
Using these formulas, we can calculate:
P(X = 6) = (10 choose 6) * 0.5^6 * 0.5^4
= 210 * 0.015625 * 0.0625
= 0.20508
Therefore, the probability of observing 6 heads out of 10 tosses of a fair coin is approximately 0.205 or 20.5%.
To calculate the probability of observing 180 heads out of 300 tosses of a fair coin using the Gaussian function, we can use the central limit theorem. According to the theorem, the sum of a large number of independent and identically distributed (in this case, the number of heads in each toss) approaches a normal distribution, with a mean equal to the sum of the means of the individual variables (np = 300 * 0.5 = 150) and a standard deviation equal to the square root of the sum of the variances of the individual variables (sqrt(np(1-p)) = sqrt(75) = 8.66).
We can then use the standard normal distribution to calculate the probability of observing 180 heads, using the formula:
P(X > 180) = P(Z > (180 - 150) / 8.66)
= P(Z > 3.47)
Using a standard normal distribution table or calculator, we can find that the probability of observing a Z-score greater than 3.47 is approximately 0.00026.
Therefore, the probability of observing 180 heads out of 300 tosses of a fair coin using the Gaussian function is approximately 0.00026 or 0.026%.
To know more about Probability:
https://brainly.com/question/30034780
#SPJ4
what is the density of the rock???!!!!!!!!!!

Answers
Answer:
he actual densities of pure, dry, geologic materials vary from 880 kg/m3 for ice (and almost 0 kg/m3 for air) to over 8000 kg/m3 for some rare minerals. Rocks are generally between 1600 kg/m3 (sediments) and 3500 kg/m3 (gabbro).
Step-by-step explanation:
What would be the angles for D, E, and F?
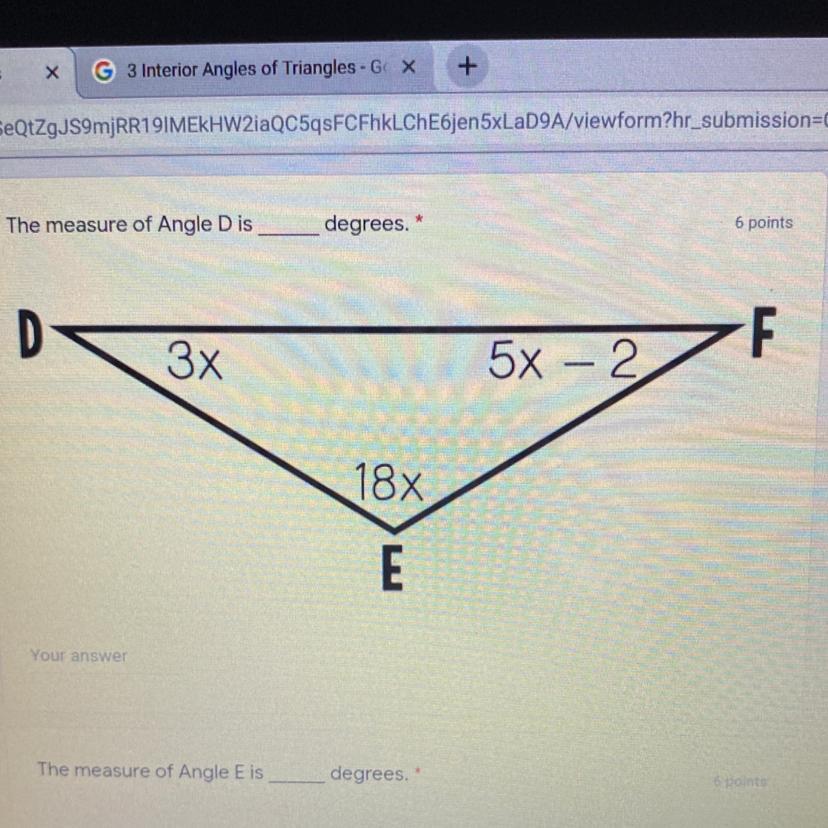
Answers
Answer:
D:21
E:126
F:33
Step-by-step explanation:
3x+18x+5x-2=180
26x-2=180
26x=182
x=7